Читайте данную работу прямо на сайте или скачайте
Особые точки и особые решения дифференциальных равнений первого порядка.
Особые точки и особые решения
дифференциальных равнений первого порядка.
Выполнил:
Курсант 315 учебной группы Кривоногов А.Н.
Проверил:
Старший преподаватель кафедры математики Доброва В.Л.
Содержание:
1.Теорема существования и единственности решения.3
2.Графическое представление теоремы о существовании единственности решенийЕЕ...4
3.Особые точки дифференциальных равнений первого порядка..5
4.Особые решения дифференциальных равнений первого порядка.7
5.Примеры,7
6.Задачи для решения..10
7.Ответы11
8.Список литературы...12
Теорема существования и единственности решения
Уравнение
 или
или  (*)
(*)
Где 




 апонимать какую-либо одну первообразную. Тогда любое решение равнения (*) запишите в виде
апонимать какую-либо одну первообразную. Тогда любое решение равнения (*) запишите в виде
Гораздо чаще приходится иметь дело с равнениями более сложного вида.


 и
и
Заменяя  ачерез
ачерез  ауравнения можно переписать в дифференциальной форме:
ауравнения можно переписать в дифференциальной форме:



Так как производную можно представить в виде отношения дифференциалов, то равнение может содержать не производную, дифференциалы неизвестной функции и независимой переменной.
Дифференциальные уравнения первого порядка в общем виде:
 (1)
(1)
Простевшие примеры показывают, что дифференциальное равнение может иметь бесчисленное множество решений. Мы наблюдали это же на примере равнения (*). Простой проверкой легко бедиться также, что равнение  аимеет решениями функции
аимеет решениями функции 
 а- функции
а- функции 
 а- любое число.
а- любое число.
Как мы видим,
в решения приведенных дифференциальных равнений входит произвольная постоянная

Придавая произвольнойа постоянной  аопределенные числовые значения, мы будем получать частные решения.
аопределенные числовые значения, мы будем получать частные решения.
Выше мы видели, что равнение  аимеет обще решение
аимеет обще решение 

 аи
аи 


 аудовлетворяет как дифференциальному равнению, так и начальному словию.
аудовлетворяет как дифференциальному равнению, так и начальному словию.
Вопрос о том, в каком случае можно тверждать, что частное решение дифференциального уравнения, довлетворяющее данному начальному словию, существует, также что оно будет единственным, выясняется теоремой.
Теорема существования и единственности решения. Если функция  анепрерывна в области,
содержащей точку
анепрерывна в области,
содержащей точку 
 аимеет решение
аимеет решение  атакое, что
атакое, что 
Если, кроме того, непрерывна и частная производная

Интересно отметить, что в словии теоремы не требуется существования производной 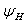
Теорема эта впервые была сформировано и доказана Коши. Поэтому часто задачу отыскания частного решения по начальным условиям называют задачей Коши.
Графическое представление теорема существования и единственности решения.
SHAPEа * MERGEFORMAT
|
0 |
|
у |
|
х |


(рис. 1) (рис. 2)
График любого частного решения дифференциального равнения называется интегральной кривой. Общему решению соответствует семейство интегральных кривых. Так как мы же проверили, что равнение  аимеет общее решение
аимеет общее решение 
 аимеет общее решение
аимеет общее решение 

Задание начального словия 

 агеометрически означает, что из семейства интегральных кривых мы выбираем ту, которая проходит через точку
агеометрически означает, что из семейства интегральных кривых мы выбираем ту, которая проходит через точку  а
а  аи
аи  анепрерывны, проходит одна единственная интегральная кривая. Если в данной точке эти словия нарушены, то это означает, что через эту точу либо вообще не проходит ни одна интегральная кривая, либо проходит несколько. Возьмем, например, равнение
анепрерывны, проходит одна единственная интегральная кривая. Если в данной точке эти словия нарушены, то это означает, что через эту точу либо вообще не проходит ни одна интегральная кривая, либо проходит несколько. Возьмем, например, равнение  видно,
что через начало координат проходит бесчисленное множество его интегральных кривых. Это противоречит теореме, так как в точке (0,0) словия теоремы существования нарушены: правая часть равнения становится неопределенной.
видно,
что через начало координат проходит бесчисленное множество его интегральных кривых. Это противоречит теореме, так как в точке (0,0) словия теоремы существования нарушены: правая часть равнения становится неопределенной.
Точки, в которых словия теоремы существования и единственности решения нарушаются, называются особыми точками.
Особые точки дифференциальных равнений первого порядка.
Прежде всего условимся переменные  аи
аи  асчитать разнонаправленными; это значит, что с равным основанием можно рассматривать
асчитать разнонаправленными; это значит, что с равным основанием можно рассматривать  акак функцию от
акак функцию от  аили
аили 

 а часть разрывна при
а часть разрывна при 
 афункцией,
афункцией,  а- независимой переменной и переписывать равнение в виде
а- независимой переменной и переписывать равнение в виде 
 а Интегральной кривой является парабола, касающаяся оси ординат в начале координат. Таким образом,
через точку (0,0) проходит одна интегральная кривая, и нам нет смысла считать эту точку особой. То же самое можно сказать. То же самое можно сказать и о любой другой точке оси абсцисс.
а Интегральной кривой является парабола, касающаяся оси ординат в начале координат. Таким образом,
через точку (0,0) проходит одна интегральная кривая, и нам нет смысла считать эту точку особой. То же самое можно сказать. То же самое можно сказать и о любой другой точке оси абсцисс.
Поэтому в дальнейшем будем считать особой только такую точку  а, в которой разрывные правые части обоих равнений
а, в которой разрывные правые части обоих равнений
 и
и 
Именно такой случай имеет место для равнений
 и
и  (2)
(2)
в начале координат. Функции в правых частях не имеют предела x и y к нулю.
Приведем несколько примеров использования равнений типа (2).
Примеры.
1) 



 аи
аи  а (рис. 2) такая особая точка называется злом.
а (рис. 2) такая особая точка называется злом.

2)
 y=0 и x=0 (рис. 3)а такая особая точк называется седлом.
y=0 и x=0 (рис. 3)а такая особая точк называется седлом.
налогичная картина будет для
решений
 аи
аи  при
при 
3) 


интегральные кривые - окружности с центром в начале координат (рис. 4). В этом случае особая точка называется центром; через нее не проходит ни одна интегральная кривая.
4)  а Замена
а Замена  априводит после
априводит после
 а с разделенными переменными
а с разделенными переменными 

 аили
аили 
 В системе полярных координат
В системе полярных координат  а
а уравнение имеет гораздо простой вида
уравнение имеет гораздо простой вида

Это семейство логарифмических спиралей (рис. 5). Особая точка такого типа называется фокусом.
Можно доказать, на чем мы не останавливаемся, что для равнения (*) начало координат при любых значениях коэффициентов(если только 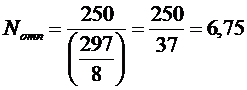
(рис. 5)
Особые решения дифференциальных уравнений первого порядка
Задача Коши для равнения (*) ставится следующим образом: задана точка 
 начальным словиям
начальным словиям


Достаточные словия существования и единственности задачи Коши дает
Теорема существования и единственности решения
Особым решением уравнения (*) на множестве I назынвается его решение
 ачерез точку его графика
ачерез точку его графика

Для существования особого решения необходимо, чтобы в области G
нарушались словия теоремы существования и единственности задачи Коши, т.е. для непрерывно диффенренцируемой функции  анеобходимо
анеобходимо
 (3)
(3)
Множество точек 
 аназывается p-диснкринминнантнным множеством равнения (*).
аназывается p-диснкринминнантнным множеством равнения (*).
График особого решения равнения (1) лежит в p-диснкриминантном множестве.
Однако p-дискриминантное множество не всегда задает особое решение:
) p-дискриминантное множество не обязано быть гладкой кривой,
б) p-дискриминантное множество не обязано определять решение уравнения (*).
Для нахождения особых решений требуется:
1. найти решение (*);
2. найти p-дискриминантное множество, исключив паранметр p из системы 
3. отобрать те из решений равнения (1), которые лежат в p-дискриминантном множестве;
4. для отобранных решений проверить выполнение опренделения особого решения, т.е.
проверить выполнение при  аусловий касания
аусловий касания 
 а- семейнство решений
(*), не совпадающих с
а- семейнство решений
(*), не совпадающих с 
Примеры решения задач.
Пример 1. Решить равнение,
найти особые решенния, начертить интегральные кривые 
1. Вводим параметр 

 (4)
(4)
Взяв полный дифференциал от обеих частей последнего равенства и заменив  ачерез
ачерез 


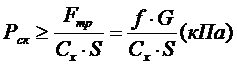
Возможны два случая:
1) 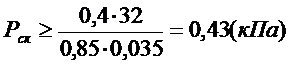
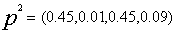

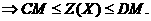
2) 


 ав (4), определяем y:
ав (4), определяем y: 


2. Найдем p-дискриминантное множество, исключив панраметр p из равнений

и

Из второго равнения системы  аследует, что
аследует, что 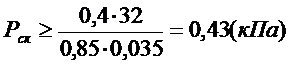
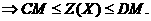
Так как 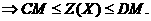 а- решение, то это кандидат в особые реншения.
а- решение, то это кандидат в особые реншения.

Рис. 6
3. Докажем, что это решение особое (проверяем касание):
 а
а аследовательно, при
аследовательно, при  ав тождество обращается второе равнение и первое равнение:
ав тождество обращается второе равнение и первое равнение: 
Через точку  апроходит решение
апроходит решение  апри
апри 
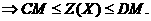 ав этой точке и не совпадающее с ним ни в какой окрестности этой точки при
ав этой точке и не совпадающее с ним ни в какой окрестности этой точки при 
Интегральные кривые представлены на рис. 6, где особое решение отмечено жирной линией.
Пример 2. Решить равнение, найти особые решенния, начертить интегральные кривые  (5)
(5)
1. Вводим параметр 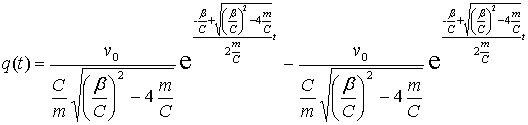

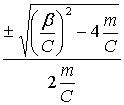
Взяв полный дифференциал от обеих частей последнего равенства и заменив 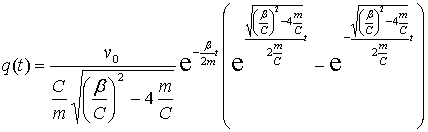 ачерез
ачерез 
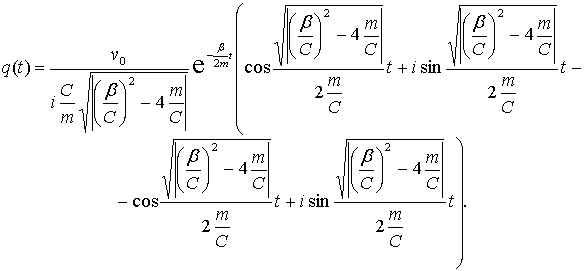

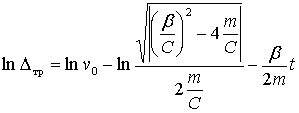
Возможны два случая:
1) 


2) 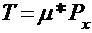



 ав (5), определяем x:
ав (5), определяем x: 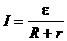



2. Найдем p-дискриминантное множество, исключив панраметр p из равнений

и
 Из второго равнения системы
Из второго равнения системы  аслендует, что
аслендует, что 

Так как  а- решение, то это кандидат в особые решенния.
а- решение, то это кандидат в особые решенния.

Рис. 7
SHAPEа * MERGEFORMAT
 а
а аследовательно, при
аследовательно, при  ав тождество обращается второе равнение и первое равнение:
ав тождество обращается второе равнение и первое равнение: 
Через точку  апроходит решение
апроходит решение  апри
апри 
 ав этой точке и не совпадающее с ним ни в какой окренстности этой точки при
ав этой точке и не совпадающее с ним ни в какой окренстности этой точки при 
Интегральные кривые представлены на рис. 7, где особое решение отмечено жирной линией.
Задачи для решения
Решить равнения, найти особые решения, начертить интенгральные кривые:
1. а
2.
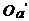
3.

4.

5.

6.

7.

8.
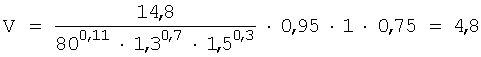
9.

10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 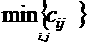
19. 
20. 
Ответы:
1.
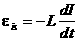 а- особое решение;
а- особое решение; 
2.
 а- особое решение;
а- особое решение; 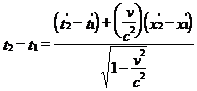
3.
 а- особое решение;
а- особое решение; 
4.
 а- особое решение;
а- особое решение; 
5.
 а- особое решение;
а- особое решение; 
6.
 а- особое решение;
а- особое решение; 
7.
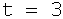 а- особое решение;
а- особое решение; 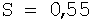
8.
 а- особое решение;
а- особое решение; 
9.
 а- особое решение;
а- особое решение; 
10.  а- особое решение;
а- особое решение; 
11.  а- особое решение;
а- особое решение; 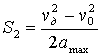
12.  а- особое решение;
а- особое решение; 
13. 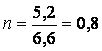 а- особое решение,
а- особое решение, 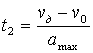

14. 
 а- особое решение,
а- особое решение, 

15.  а- особое решение,
а- особое решение, 
16. 
 а- особое решение,
а- особое решение, 

17. 
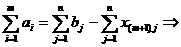 а- особые решения,
а- особые решения,
18. 
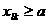 а- особое решение,
а- особое решение, 
19.  а- особое решение,
а- особое решение, 
20. 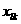
 а- особые решения,
а- особые решения,
а
Список литературы
Краткий курс математического анализа для ВТУЗВа А.Ф.Бермант, И.Г. Араманович

