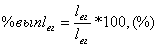Читайте данную работу прямо на сайте или скачайте

Метод релаксации переменных при решении систем линейных равнений

Вступ

Бурхливий розвиток новтньо

Сьогодн серйозн компанÿ працюють над новими мовами програмування й засобами реалзацÿ коду. Так, завдяки Б.Страуструпу було ведено обТ

ктно - орúнтоване програмування, створений

У сво

му проект я буду використовувати Borland C++ версÿ 4.5, тому що вважаю його найбльш оптимальним для поставлено

1.1 Загальна характеристика методв ршення систем нйних рвнянь.

Способи виршення систем лнйних рвнянь в основному роздляються на дв групи: 1) точн методи, що представляють собою кнцев алгоритми для обчислення корнь системи ( до таких методв ставляться: правило Крамера, метод Гаусса, метод головних елементв, метод квадратних корнь н.), 2) терацйн методи, що дозволяють одержувати корнь системи з заданою точнстю, шляхом збжних нескнченних процесв (до

Внаслдок неминучих округлень результати навть точних методв

наближеними, причому оцнка погршностей корнь у загальному випадку скрутна. При використанн терацйних процесв, поверх того, дода

ться погршнсть методу.

Однак ефективне застосування терацйних методв стотно залежить вд вибору початкового наближення й швидкост збжност процесу.

1.2 Метод релаксацÿ змнних систем нйних рвнянь

П.З.:

Дана система нйних рвнянь, необхдно знайти ата н.

Нехай ма

мо наступну систему нйних рвнянь:

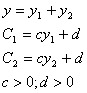(1)

Перетворимо цю систему в такий спосб: перенесемо вльн члени воруч роздлимо перше рвняння на - 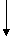а т.д. Тод одержимо систему, приготовлену до релаксацÿ,

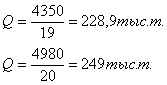(2)

де

аи.

Нехай апочаткове наближення ршення системи (2). Пдставляючи ц значення в систему (2), одержимо нев'язання

(3)

Якщо одн㺿 з невдомих адати прирст азменшиться на величину азбльшаться на величини ав 0, досить величин адати прирст

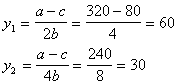
ми будемо мати:

и

апри

Метод релаксацÿ (по-росйському: ослаблення) у його найпростшй форм поляга

в тм, що на кожному кроц перетворюють у нуль максимальну по модул нев'язання шляхом змни значень вдповдного компонента наближення. Процес закнчу

ться, коли вс нев'язання останньо

1.3 Використання метода релаксацÿ змнних в системах нйних рвнянь на приклад

Приклад. Методом релаксацÿ виршити систему

(4)

роблячи обчислення з двома десятковими знаками.

Ршення. Приводимо систему (4) до виду, зручному для релаксацÿ

Вибираючи як початков наближення корнь нульов значення

Знаходимо вдповдн

Вдповдно до загально

Звдси одержу

мо нев'язку

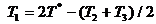
	0	0,60	0	0,70	0	0,80
		0,16		0,16		-0,80
		0,76		0,86		0
		0,17	0,86	-0,86		0,09
		0,93		0		0,09
	0,93	-0,93		0,09		0,09
		0		0,09	0,18	0,18
		0,04		0,04		-0,18
		0,04	0,13	0,13		0
		0,03		-0,13		0,01
	0,07	0,07		0		0,01
		-0,07		0,01		0,01
		0		0,01	0,02	0,02
		0		0		-0,02
		0
		0	0,01	0,01		0
		0		-0,01		0
		0		0		0
	1,00		1,00		1,00

Дал, дума

мо

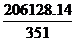
т.д. Вдповдн результати обчислень наведен в таблиц.

Пдсумовуючи вс прирости

Для контролю пдставля

мо знайден значення корнь у вихдн рвняння; у цьому випадку система виршена точно.

Висновки

Я навчився розвТязувати системи нйних рвнянь методом релаксацÿ змнних, та закрпив отриман навички розробкою програми на мов Borland C++ 4.5.

Додаток А

Виршити систему нйних рвнянь методом релаксацÿ змнних.

Лстинг програми 1.1:

#include<iostream.h>

#include<math.h>

int maximal(int n,double R0[]);

void main(){

int i,j,n,f,k,iter;

double S,det;

cout<<"Введите размерность матрицы(матрица должна быть квадратной)= ";cin>>n;

double *x=new double [n];

double **b=new double *[n];

for(i=0;i<n;i++)

b[i]=new double[n+1];

double **a=new double *[n];

for(i=0;i<n;i++)

a[i]=new double[n+1];

cout<<"Введите количество итераций:";

cin>>iter;

cout<<"Введите расширенную матрицу:\n";

for(i=0;i<n;i++){

for(j=0;j<=n;j++)

cin>>b[i][j];

}

cout<<"Подготавливаю матрицу к релаксации...\n";

for(i=0;i<n;i++){

for(j=0;j<n;j++)

a[i][j]=-b[i][j]/b[i][i];

a[i][n]=b[i][n]/b[i][i];

}

for(i=0;i<n;i++){

for(j=0;j<n+1;j++)

cout<<"а "<<a[i][j]<<" || ";

cout<<"\n";

}

double *x0=new double [n];

for(i=0;i<n;i++)

x[i]=0.0;

double *R0=new double [n];

cout<<"Введите значения начальных приближений:\n";

for(i=0;i<n;i++)

cin>>x0[i];

S=0.0;

for(i=0;i<n;i++){

for(j=0;j<n;j++)

S=S+a[i][j]*x0[i];

}

for(i=0;i<n;i++){

R0[i]=a[i][n]-x0[i]+S;

cout<<"R("<<i<<")="<<R0[i]<<" | ";

}

f=maximal(n,R0);

det=R0[f];

for(k=0;k<iter;k++){

cout<<"det{"<<k<<"}="<<det<<"\n";

for(i=0;i<n;i++){

if(i!=f) R0[i]=R0[i]+a[i][f]*det;

аelse R0[i]=R0[i]-det;

}

for(i=0;i<n;i++)

cout<<"R["<<i+1<<"]="<<R0[i]<<" ";

x[f]=x[f]+det;

f=maximal(n,R0);

det=R0[f];

}

cout<<"\n";

for(i=0;i<n;i++)

cout<<"X{"<<i+1<<"}="<<x[i]<<"\n";

delete []x;

delete []R0;

delete []x0;

delete []a;

}

int maximal(int n,double R0[]){

int i,f;

f=0.0;

for(i=0;i<n-1;i++){

if(R0[i+1]>R0[i]) f=i+1;

}

return f;

}