Метод последовательных ступок (Теория принятия решений)

ПЛАН

Введение	3
Суть метода последовательных ступок	4
Порядок решения детерминированных многокритериальныха задач методом последовательных ступок	5
Исследование метода последовательных ступок	9
Список использованной литературы.	19

ВВЕДЕНИЕ

Вопросы принятия наилучших (оптимальных) решений стали в настоящее время весьма актуальнными, особенно в экономике, технике, военном деле и других областях человеческой деятельности.

Задачи отыскания наилучших (или хотя бы довлетворительных) путей достижения поставленных целей являются основными в новом разделе наунки - исследовании операций, - который тесно свянзан с различными математическими дисциплинами, в том числе теорией игр, математическим программированием и теорией оптимальных процессов, теорией вероятностей и многими другими.

СУТЬ МЕТОДА ПОСЛЕДОВАТЕЛЬНЫХ УСТУПОК

Процедура решения многокритериальной задачи методом последовательных ступок заключается в том, что все частные критерии располагают и нумеруют в порядке их относительной важности; максимизируют первый, наиболее важный критерий; затем назначают величину допустимого снижения значения этого критерия и максимизируют второй по важности частный критерий при словии, что значение первого критерия не должно отличаться от максимального более чем на величину становленного снижения (уступки); снова назначают величину ступки, но же по второму критерию и находят максимум третьего по важности критерия при словии, чтобы значения первых двух критериев не отличались от ранее найденных максимальных значений больше чем на величины соответствующих уступок; далее подобным же образом поочередно используются все остальные частные критерии; оптимальной обычно считают любую стратегию, которая получена при решении задачи отыскания условного максимума последнего по важности критерия.

Таким образом, при использовании метода последовательных ступок многокритериальная задача сводится к поочередной максимизации частных критериев и выбору величин ступок. Величины ступок характеризуют отклонение приоритета од них частных критериев перед другими от лексикографического: чем ступки меньше, тем приоритет жестче.

ПОРЯДОК РЕШЕНИЯ ДЕТЕРМИНИРОВАННЫХ МНОГОКРИТЕРИАЛЬНХа ЗАДАЧ МЕТОДОМ ПОСЛЕДОВАТЕЛЬНЫХ СТУПОК

При решении многокритериальной задачи метондом последовательных уступок вначале производитнся качественный анализ относительной важности частных критериев; на основании такого анализа критерии располагаются и нумеруются в порядке бывания важности, так что главным является критерий K₁, менее важен. K₂, затем следуют остальные частные критерии К₃, К₄..., K_S. Максимизируется первый по важности критерий K₁ и определяется его наибольшее значение Q₁. Затем назначается величина допустимого снижения (уступки) D₁>0 критерия K₁ и ищется наибольшее значение Q₂ второго критерия K₂ при условии, что значение первого критерия должно быть не меньше, чем Q₁ЧD₁. Снова назначается величина ступки D₂>0, но же по второму критерию, которая вместе с пернвой используется при нахождении словного максинмума третьего критерия, и т. д. Наконец, максиминзируется последний по важности критерий Ks при словии, что значение каждого критерия К_r из SЧ1 предыдущих должно быть не меньше соответствуюнщей величины Q_rЧD_r ; получаемые в итоге стратенгии считаются оптимальными.

Таким образом, оптимальной считается всякая стратегия, являющаяся решением последней задачи из следующей последовательности задач:

1) найти Q₁=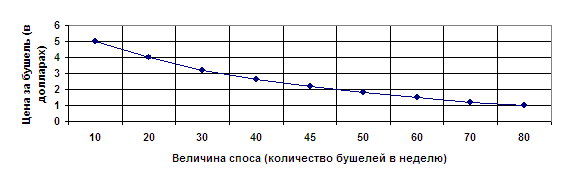а

(1)

2) найти Q₂=а

..

3) найти Q_S=а

Если критерий K_S на множестве стратегий, довнлетворяющих ограничениям задачи S), не достигает своего наибольшего значения Q_s, то решением мнонгокритериальной задачи считают максимизируюнщую последовательность стратегий {u^k} из казаого множества (lim K_S(u^k) = Q_S).

k->¥

Практически подобные максимизирующие послендовательности имеет смысл рассматривать и для тонго случая, когда верхняя грань в задаче S) достингается, так как для решения экстремальных задач широко применяются итеративные методы.

Величины уступок, назначенные для многонкритериальной задачи, можно рассматривать как своеобразную меру отклонения приоритета (степени относительной важности) частных критериев от жесткого, лексикографического.

Величины ступок D_r последовательно назначанются в результате изучения взаимосвязи частных критериев.

Вначале решается вопрос о назначении величинны допустимого снижения D_r первого критерия от его наибольшего значения Q₁. Практически для этонго задают несколько величин ступок D¹₁, D²₁, D³₁Е и путем решения 2) в задаче (1) определяют соответствующие макс. значения Q₂(D¹₁), Q₂(D²₁), Q₂(D³₁), и второго критерия. Иногда, если это не слишком сложно, отыскивается функция Q₂(D₁). Результаты расчетов для наглядности Представляем графически (Рис 1)

	Рис 1

Он показывает, что вначале даже небольшие величины ступок позволяют получить существенный выигрыш по втонрому критерию; с дальнейшим величением ступки выигрыш растет все медленнее. На основе анализа полученных данных и решают вопрос о назначении величины ступки D₁, а затем находят Q₂(D₁).

Далее рассматривают пару критериев K₂ и K₃ вновь назначают пробные величины ступок Q₂(D²₂),, ... и, решая 3) в задаче (1), отыскивают наибольшие значения третьего критерия Q₃(D¹₂), Q₃(D²₂),... Полученные данные анализируют, назначают D₂, переходят к следующей паре критеринев К₃, K₄ и т. д.

Наконец, в результате анализа взаимного влиянния критериев K_S-1 и K_S выбирают величину понследней ступки D_S-1 и отыскивают оптимальные стратегии, решая S) в задаче 1 (обычно ограничиванются нахождением одной такой стратегии).

Таким образом, хотя формально при использонвании метода последовательных ступок достаточно решить лишь S задач (1), однако для назначенния величин ступок с целью выяснения взаимосвянзи частных критериев фактически приходится реншать существенно большее число подобных задач.

ИССЛЕДОВАНИЕ МЕТОДА ПОСЛЕДОВАТЕЛЬНЫХ СТУПОК

Во введении при изучении отношения предпочнтения ³, порождаемого векторным критерием, бынло выяснено, что в качестве оптимальных вообще могут выступать лишь эффективные стратегии. Понэтому возникают естественные вопросы: всегда ли использование метода последовательных ступок приводит к получению эффективных стратегий, если не всегда - то в каких случаях (при выполннении каких словий) можно гарантировать полунчение лишь эффективных стратегий?

Оказывается, что метод последовательных стунпок не всегда приводит к выделению лишь эффекнтивных стратегий, т. е. решениями S) из задачи (1) могут быть и неэффективные стратегии. Это легко подтвердить простым примером.

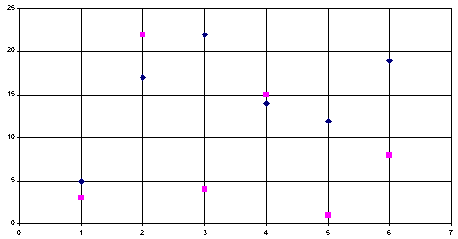
Пример 1. Пусть множество UÌR³ Ч многогранник, изображенный на рис.2, K₁(u)=u1, K₂(u)=u_2, K₃(u)=u₃. Здесь решением 3 из задачи (1) является любая точка треугольника ABC (на рисунке он заштрихован), но эффекнтивны лишь точки отрезка АС.

Справедливо, однако, тверждение: если u* - единственная (с точностью до эквивалентности) стратегия, являющаяся решением S) из задачи (1), то она эффективна.

Действительно, предположим, что стратегия u* неэффективна, так что существует стратегия u'>u*. Но стратегия u' также довлетворяет всем огранниченияма S) задачи (1) и доставляет кринтерию K_S значение Q_s; иначе говоря, u' оказыванется решением этой заданчи, что противоречит снловию единственности u*. тверждение доказано.

Рис 2

Можно доказать такна же, что если UÌRⁿ занмкнуто и ограничено, К_r непрерывны на U, стратегия, являющаяся решенниема S) задачи (1), единственна с точностью до эквивалентности, то любая максимизирующая последовательность, служащая решением S), эффективна.

Пример 2. Пусть UÌRⁿ Ч выпуклое множество,

все К_rа квазивогнуты. При этих словиях множество стратегий, удовлетворяющиха ограничениям r) задачи (1), также выпукло (r=1,2,..., S), так что каждая из задач 1), 2),..., S)а является задачей квазивогнутого программирования. Если Ks строго квазивогнут, то решением задачи S) может служить лишь единственная и потому эффективная стратегия;а если же |при этом U замкнуто и ограничено, все К_r непрерывны на U, то любая максимизирующая последовательность, являющаяся решением S), эффективна.

Пример 3. Предположим, что из многогранника U задачи, описанной в примере 1, далена вся грань А'В'С', но оставлена точка В. Теперь эта точка оказывается единственным решениема 3) задачи (1). Здесь точка В, конечно, эффективна. Любая сходящаяся к ней последовательность внутренних точек многогранника, довлетворяющих ограниченниям задачи 3), будет максимизирую щей для Ks, но не будет эффективной. Указанное положение - следствие не замкнутости рассматриваемого в данном примере множества U.

В связи с тем, что не всегда стратегия, получеая с помощью метода последовательных ступок, является эффективной, возникает и такой вопрос: обязательно ли среди множества стратегий, выденляемых этим методом, существует хотя бы одна эффективная?

В общем случае на этот вопрос положительный ответ дать нельзя, однако имеет место такое тверждение: если UÌRⁿ - множество замкнутое и ограниченное, все К_r непрерывны, то решениема S) задачи (1) служит по крайней мере одна эффективная стратегия.

Действительно, при выполнении словий этого утверждения множество U^s стратегий-решений S) оказывается непустым, замкнутым и огранниченным. Следовательно, существует точка u*ÎU^S, в которой функция достигает наибольшего на U^s значения. Нетрудно убедиться в том, что u* эффективна.

Таким образом, при решении почти всякой принкладной многокритериальной задачи метод последонвательных ступок выделяет в качестве оптимальнных и эффективные стратегии. Однако необходимо отметить, что выделенные эффективные стратегии не обязаны быть эквивалентными (см. пример 1); но нетрудно проверить, что это возможно лишь при S³3.

Если нельзя гарантировать, что при решении рассматриваемой многокритериальной задачи метод последовательных ступок приводит к получению лишь эффективных стратегий (в частности, если по выполняется вышеприведенное словие единстнвенности), то для выделения эффективной стратенгии среди решений задачи S) достаточно, как поканзывает только что проведенное доказательство,

найти (2)

Однако апрактически более добно применять такой прием : заменить ва S) критерий K_s на а,

где À - положительное число;

в результате получится задача:

(3)

Нетрудно доказать, что любая стратегия, являющаяся решением задачи (3), эффективна; более того, всякая максимизирующая последовательность, служащая решением этой задачи, также эффективна.

Смысл казанного приема заключается в том, что при достаточно малом числе À>0 для любой полученной в результате решения задачи (3) стратегии w значение критерия K_S(w) будет весьма близким к Q_s^*) и эта стратегия эффективна, в то время как при решении S) задачи (1) может быть получена стратегия и, которую выгодно заменнить некоторой эффективной стратегией v>u, сунщественно лучшей, чем и, но одному или даже ненскольким частным критериям. А поскольку величинны ступок А, на практике станавливаются принближенно, то замена Ks н K*_s при малых À>0 в силу казанной причины оказывается допустимой и оправданной.

Таким образом, понятие эффективной стратегии позволило точнить вычислительную процедуру отыскания оптимальных стратегий методом послендовательных ступок.

С другой стороны, метод последовательных ступок позволяет казать характеристическое свойство эффективных стратегий.

Теорема 1.

Для любой эффективной стратегии u* существуют такие числа D^*_r, что эту стратегию можно выделить методом последовательных ступок, т. е.
при D_r=D^*_r, r=1, 2,...,SЧ1, стратегия u* являетнся единственным (с точностью до эквивалентности) решениема S) задачи (1).

Теорема 1 характеризует эффективные странтегии с помощью последовательности задач (1). В частности, она показывает, что метод последовантельных ступок можно использовать для построенния множества эффективных стратегий.

Более того, теорема 1 позволяет исследовать и сам метод последовательных ступок. Действинтельно, она показывает, что при любом фиксироваом расположении частных критериев, по степени относительной важности одним лишь выбором венличин ступок можно обеспечить выделение любой эффективной стратегии в качестве оптимальной (так что проблема отыскания оптимальной стратенгии, т. е. проблема выбора эффективной стратегии из всего множества U

Следовательно, для решения многокритериальнной задачи нужно так ранжировать критерии, чтобы потом добнее было выбирать величины ступок. учитывая вышеизложенное и внимательно рассмонтрев порядок назначения величин ступок, можно сделать следующий вывод: метод последовательных ступок целесообразно применять для решения тех многокритериальных задач, в которых все частные критерии естествеым образом упорядочены по степени важности, причем каждый критерий настолько существенно более важен, чем последующий, что можно огранинчиться четом только попарной связи критериев и выбирать величину допустимого снижения очереднного критерия с учетом поведения лишь одного слендующего критерия.

Особенно удобным является случай, когда же в результате предварительного анализа многокритериальной задачи выясняется, что можно допустить ступки лишь в пределах линженерной точности (Ч10% от наибольшей величины критерия).

Решение многокритериальной задачи методом последовательных ступок - процедура довольно трудоемкая, даже если заранее выбраны величины всех ступок. Поэтому большой интерес представляет вопрос: можно ли при заданных D_i получить оптимальную стратегию за один этап, сведя послендовательность задач (1) к одной экстремальной задаче?

Мы можем казать лишь приближенный способ одноэтапного решения для S=2. Он основан на следующем тверждении:

Лемма 1.

Пусть множество UÌR^p замкнуто и ограничено, K₁и К₂ непрерывны на U, D₁³0 и À£ D₁/M¹₂, где

Тогда для любой стратегии u*, доставляющей функции L=K₁+ÀК₂ наибольшее на U значение, справедливо неравенство Q₁-K₁(u*)£ D₁ причем если K₁(u*)£ Q₁, то

Эт лемма, показывает, что если решить задачу максимизации на U функции L=K₁+ÀК₂, в котонрой число À назначено казанным образом, то для полученной стратегии u* (она обязательно эффекнтивна)а значение K₁(u*)а будет отличаться от максимального Q₁ не более, чем на D₁, a K₂(u*) будет тем ближе к Q₂, чем точнее назначена оценка М¹₂.

Однако даже если взять число М¹₂, удовлетворяюнщее (4) как равенству, и положить À = D₁/M¹₂, то все равно нельзя гарантировать, что K₂(u*)=Q₂, так что рассматриваемый способ действительно является приближенным.

Пример 4. Пусть U - четверть единичного круга, ленжащая в положительном квадранте: U={u: uÎR₂, u²₁+u²₂£1, u₁³0, u₂³0} K₁(u)=u₁, K₂(u)=u₂. Здесь Q₁ = l и М¹₂=1, если исходить из (4) как равенства. Примем D₁=0,2; À=0,2.

Функция u₁ + 0,2u₂ достигает максимума на U в единственной точке 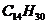а, однако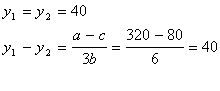

Пример 5. U={u: uÎR_{2 ,} 0£u₂£1, (1+d)u₂£1-u₁} где d Ч положительное число, K₁(u)=u₁, K₂(u)=u₂ . Испольнзуя (4) как равенство, находим: М¹₂ = 1. Положим D₁=1; À=1. Функция u₁+u₂ достигает на U максимума в единнственной точке (1, 0). Возьмем теперь ; À=1 + e. где eЧ любое сколь годно малое положительное число. Тогда при d<e функция u₁+(1+e)u₂ будет достигать максимума на U в точнке (-d, 1), так

что Q₁-K₁(-d, 1) = 1+d >D₁=1.

Примечание. Для решения многокритериальных задач иногда применяют метод выделения основного частного кринтерия. Этот метод состоит в том, что исходная многокритеринальная задача сводится к задаче оптимизации по одному частному критерию К_L, который объявляется основным, или главным, при словии, что значения остальных частных кринтериев К_r должны быть не меньше некоторых становленных величин (лтребуемых значений) b_r, т. е. к задаче

найти (5)

причем оптимальной считается обычно всякая стратегия, явнляющаяся решением задачи (5).

Выделение критерия K_t в качестве основного и назнанчение пороговых величин b_r, для остальных частных критериев фактически означает, что все стратегии разбиваются на два класса. К одному относятся стратегии, которые довлетворяют всем SЧ1 ограничениям K_r(u)³b_r; такие стратегии можно назвать допустимыми. К другому классу относятся такие стратегии, которые не довлетворяют хотя бы одному из казаных SЧ1а неравенств. Наконец, среди допустимых стратегий предпочтительнее считается та, для которой значение Критерия K_l больше.

Необходимо отметить, что становившееся название Ч лоснновной, или главный критерий - по существу весьма словно. Действительно, критерий K_l амаксимизируется на множестве лишь допустимых стратегий; иначе говоря, если для стратегии u значение некоторого второстепенного частного критерия K_r оказывается хоть немного меньше, чем b_r, то она же не может претендовать н роль оптимальной, сколь бы большим ни было для нее значение основного критерия. Сравнение (5)а и (1) показывает, что метод послендовательных ступока формально можно рассматривать как особую разновидность метод выделения основного частного критерия, отличающуюся наличием специфической процедуры назначения величин ограничений для задачи максимизации K_S (это обстоятельство фактически же использовалось при доказательстве теоремы 1).

Поэтому все полученные выше результаты, связанные с вопросами выделения эффективных стратегий методом последовательных ступок, переносятся и на рассматриваемый метод. В частности, этот метод выделяет лишь эффективные стратегии, когда решение задачи (5) единственно с точностью до эквивалентности; если же справедливость казанного словия единственности не становлена, то целесообразно в (5) заменить K_l на

À>0 - достаточно малое число.

Выбор конкретной эффективной стратегии из множества U⁰ формальнно эквивалентен назначению надлежащих величин b_r, причем в качестве основного можно выбрать любой частный критенрий.

Это означает, с одной стороны, что рассматриваемый метод ниверсален в том смысле, что он позволяет для каждой ммногокритериальной задачи выделить в качестве наилучшей любую эффективную стратегию.

Это же означает, с другой стороны, что вопросы о выборе одного из частных критериев в качестве основного и назначении минимально допустимых величин b_r для остальных критериев нужно решать совместно, ибо какой бы частный критерий ни был выбран основным, только лишь назначением величин ограничений на остальные критерии можно обеспенчить получение в качестве оптимальной любой (намеченной) эффективной стратегии.

Таким образом, предварительное выделение одного из чанстных критериев основным еще никак не меньшает свободы выбора эффективной стратегии (так что название лосновной, или главный критерий действительно весьма словно). Слендовательно, при качественном анализе конкретной многокринтериальной задачи вопрос о выделении одного из частных критериев в качестве основного следует решить так, чтобы облегчить назначение величин ограничений на остальные частные критерии.

Практически назначается серия наборов {b_r} пороговых значений и для каждого набора отыскивается соответствуюнщее наибольшее значение основного критерия (при этом слендует учитывать данные выше рекомендации, относящиеся к обеспечению (получения лишь эффективных стратегий, а такнже иметь в виду, что при произвольно назначенных числах b_r может случиться, что задача (5) вообще не имеет смыснла, так как ни одна стратегия не довлетворяет входящим в нее ограничениям).

Далее на основании анализа полученной серии значений всех частных критериев (т. е. асерии значений векторного кринтерия) производится окончательное назначение величин огранничений, чем определяется и выбор стратегии, которая и бундет считаться оптимальной.

Рассмотрение казанной процедуры назначения величин ограничений показывает, что расчет серии значений всех частных критериев фактически имеет целью получение представления о множестве эффективных стратегий (или некоторонго его подмножества) с помощью ряда отдельных точек, зантем эта информация служит для окончательного выбора странтегии (производимого на основании интуиции, здравого смыснла и т. п.).

Следовательно, метод выделения основного частного критерия стоит применять лишь в том случае, когда имеются соображения о примерных значениях величин b_r, (или о донвольно зких пределах этих значений), позволяющие огранничиться рассмотрением сравнительно небольшой части всего множества эффективных стратегий.

Список использованной литературы.

1) Подиновский В.В., Гаврилов В. М. Оптимизация по последовательно применяемым критериям. М., Сов. радио, 1975, 192 стр.