Читайте данную работу прямо на сайте или скачайте

Метод моментов в определении ширины линии магнитного резонанса

Оглавление

.Введени..2

з1.Локальное пол2

з2.Общая теория магнитного поглощения2

Б. Уширение, вызванное взаимодействием между одинаковыми спинамиЕЕ.5

з3.Диполь-дипольное взаимодействи...5

з4.Определение моментов6

з5.Метод вычисления моментов.7

В. Кинетические свойствЕ.10

з6.Кинетическое уравнени10

з7.Электропроводность...11

. ВВЕДЕНИЕ

Линия магнитного резонансного поглощения системы спинов, находящихся в неоднородном магнитном поле, обладает некоторой шириной, обусловленной разбросом ларморовских частот. Аналогичное ширение может иметь место в неидеальных кристаллах благодаря взаимодействию ядерных квадрупольных моментов с малыми градиентами электрического поля, значения которых изменяются от одного зла решетки к другому случайным образом. В обоих случаях ширина линии обусловливается различием резонансных частот отдельных спинов, не взаимодействиями между ними. Соответствующее ширение линии называется неоднородным ширением.

Положение существенно изменяется, если уширение линии обусловлено взаимодействием между соседними спинами. Эта задача и рассматнривается в настоящей работе.

з 1. ЛОКАЛЬНОЕ ПОЛЕ

Энергия взаимодействия между двумя ядерными спинами зависит от величины и ориентации их магнитных моментов, также от длины и направления вектора, описывающего их относительное расположение. Влияние такого взаимодействия на ширину линии поглощения сущестнвенным образом зависит от того, зафиксирован ли этот вектор в пространнстве или его положение быстро меняется со временем вследствие относинтельного движения ядер.

Последний случай, как правило, встречающийся в жидкостях и ганзах, будет рассмотрен позднее. В этой главе мы ограничимся случаем жестнкой решетки, в которой ядра можно считать неподвижными. Такое принближение разумно для многих твердых тел при комнатной температуре, в частности для ионных кристаллов.

Энергия диполь-дипольного взаимодействия двух магнитных моментов m₁=g₁ЮI₁ и m₂=g₂ЮI₂а описывается хорошо известным выражением

(1)

которое можно переписать в виде

W₁₂ = - m₂ ∙H₁₂ = - g₂ЮI₂∙H₁₂,

где H₁₂ - локальное поле, созданное первым спином в месте расположенния второго спина. (Введение в рассмотрение понятия локального поля очень добно.) Поскольку ядерные магнитные моменты имеют порядок 10^-3 магнетона Бора, или 10^-23 CGS, между ядерные расстояния порядка нескольких ангстрем, то локальные поля в жесткой решетке в общем случае имеют порядок нескольких эрстед.

Взаимодействие двух одинаковых диполей в сильном поле Н₀ может быть описано с классической точки зрения следующим образом. Первый диполь m₁ прецессирует с ларморовской частотой вокруг поля Н₀ и, следовантельно, обладает постоянной составляющей вдоль этого поля и составляюнщей, которая вращается в плоскости, перпендикулярной полю. Постояя составляющая m₁ создает в месте расположения диполя m₂ слабое постоянное поле, ориентация которого относительно Н₀ зависит от взаимнного расположения спинов. Если поле Н₀ сильное, то на него заметно влияет только параллельная или антипараллельная ему составляющая слабого поля. Так как каждый спин в решетке имеет несколько соседей с различными относительными положениями и ориентациями, постоянная составляющая локального поля имеет разные значения в различных местах, что приводит к разбросу ларморовских частот и ширению линии.

Вращающаяся составляющая m₁ создает в месте расположения m₂ локальное магнитное поле, вращающееся с ларморовской частотой m₁, которая совпадает с ларморовской частотой для m₂. В свою очередь она имеет составляющую в плоскости, перпендикулярной Н₀ и, следовательно, может заметно изменять ориентацию m₂ благодаря явлению резонанса. Соответствующая ширина линии должна быть порядка величины вращающегося поля. В рассматринваемом случае оно того же порядка величины, что и локальное постоянное поле и, следовательно, вносит в ширение вклад сравнимой величины.

Необходимо отчетливо понимать, что механизмы, обусловливающие эти вклады в ширину линии, в действительности различны. Если два спина не являются одинаковыми, то вращающееся поле, созданное m₁, не является резонансным для m₂а и оказывает на него пренебрежимо малое влияние, в то время как постоянное поле, созданное m₁, в месте располонжения m₂ является столь же эффективным, как и в случае одинаковых спиннов. При прочих равных словиях одинаковые соседние спины оказывают более сильное влияние на ширение резонансной линии, чем неодинанковые.

з 2. ОБЩАЯ ТЕОРИЯ МАГНИТНОГО ПОГЛОЩЕНИЯ

Для количественного описания формы линии, обусловленной дипольным ширением, необходимо развить формализм.

Когда все спины образца связаны друг с другом дипольным взаимондействием, представление об отдельных независимых спинах, находящихся в стационарных состояниях, становится неверным. Этот вывод следует хотя бы из того факта, что вращающееся локальное поле, созданное одним спином, приводит к переориентации его соседей. Поэтому образец принходится рассматривать как единую большую систему спинов, переходы, вызванные радиочастотным полем, - как переходы между различными энергетическими ровнями этой системы. Соответственно изменяется и стантистическое описание с использованием матрицы плотности. Вместо стантистического ансамбля спинов, описываемых (2I +1) ´ (2I +1) матринцей плотности, весь образец, содержащий N спинов, теперь становится одним элементом статистического ансамбля и описывается (2I +1)^N ´ (2I +1)^N матрицей плотности. Такое видоизменение никоим образом не ограничивается ядерным магнетизмом, напротив, оно весьма часто встренчается в статистической физике именно всякий раз, когда переходят от описания систем со слабыми взаимодействиями, например, таких, как молекулы газа при низком давлении, к описанию сильно взаимодействуюнщих систем, таких, как атомы Кристалла. Первый подход соответствует методу Максвелла - Больцмана, второй - методу Гиббса.

Стационарное состояние, следуя методу Гиббса, можно описать слендующим образом. Если к системе спинов приложено линейно поляризоваое вдоль оси Ох радиочастотное поле Н₁ cos wt, то при стационарных словиях система приобретает намагниченность, составляющая которой вдоль этой же оси равна

М_х = H₁ {c' (w) cos wt +c'' (w) sin wt}. (la)

Условие линейности или отсутствия насыщения предполагает, что c' и c'' не зависят от H₀. c' и c'' можно измерить отдельно, c'' пропорционально скорости поглощения радиочастотной энергии образцом.

Выведем общую формулу для c'' (w). Выше было показано, что в линейнной теории резонанса между c' (w) и c'' (w) существуют независимо от принроды рассматриваемой системы общие соотношения (соотношения Крамерса - Кронига), позволяющие вычислить одну из этих величин, когда для всех значений частоты известна другая.

Ниже, чтобы избежать путаницы, мы будем обозначать через М макронскопическое значение намагниченности образца и через M - соответнствующий квантовомеханический оператор. Между ними имеет место соотношение

М = <M> = Sp {rM}, (2)

где r - статистический оператор, или матрица плотности, описывающая систему спинов. Пусть ħH - полный гамильтониан системы в отсутствие внешнего радиочастотного поля. Если до приложения радиочастотного поля система находится в тепловом равновесии при температуре Т, то ее статистический оператор определяется выражением

(3)

которое просто означает, что статистическое поведение системы можно описать, если ее энергетическим ровням ħE_n приписать населенности, пропорциональные exp(ЧħE_n/kT).

При наличии радиочастотного поля равнение движения для r имеет вид

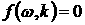(4)

где V - объем образца. Чтобы решить (4) относительно r, сделаем подстановку

r* = e^{i H t}r e ^{- i H t} , (5)

которая преобразует (4) в равнение

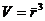. (6)

Предположим, что радиочастотное поле было включено в момент, когда образец находился в тепловом равновесии и

r (Ц¥) = r = r* (Ц¥).

В момент t решение (6) в линейном приближении относительно Н₁ имеет вид

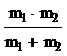( 7)

Поэтому, возвращаясь к r [см. (5)], находим

(8)

Если предположить, что до включения радиочастотного доля намагнинченность вдоль оси x была равна нулю, т. е.

М_х (Ц¥) = Sp {r₀M_x} =0,

то

(9)

и, согласно определению (1 а),

(10)

Учтем, что температура обычно достаточно высока для того, чтобы для равнновесной матрицы плотности (3) можно было использовать линейное разложение

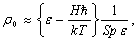
где e - единичный оператор; тогда восприимчивость c²(w) становится равной

(11)

откуда, интегрируя по частям, получаем

(12)

Выражение (12) можно преобразовать к более компактной форме двумя способами.

В первом способе, вводя в рассмотрение оператор Гейзенберга

M_x (t) = e ^{iH t} M_x e ^{Ц iH t}, (12a)

можно переписать (12) в виде

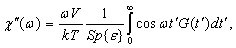(13)

где

G(t) = Sp{M_x(t) M_x }, (13a)

Функцию G(t) назовем функцией корреляции, или функцией релаксации намагниченности системы.

Во втором способе выражение (12) можно переписать в виде

Отсюда после применения хорошо известной формулы для d-функции

получаем

(14)

где суммирование S¢ производится только по тем энергетическим ровням, для которыха | E_n ЧE_n' | = ħw. Обычно, вводя в рассмотрение вероятнности переходов, выражение (14) используют как отправную точку для вывода (13) с помощью интегрального представления d-функции. Из равенства (14) в общем виде следует, что функция формы f(w), определяющая форму линии, пропорциональна сумме S¢ |< п | M_x | nТ >|². Точная зависимость этого выражения от co вытекает из условия, ограничинвающего суммирование только по тем ровням, для которых | E_n ЧE_n' | = ħw. Формулы (13) и (14) являются весьма общими и справедливы в случае, когда спектр магнитного поглощения системы содержит одну или несколько острых резонансных линий, т. е. в случае ядерного магннитного резонанса. Математически это словие может быть сформулиронвано следующим образом.

Гамильтониан ħH системы представляет собой сумму главной части ħH₀ аи малой возмущающей части, которую добно записать в виде ħeH₁, где e - параметр малости возмущения. В отсутствие H₁ спектр поглощенния системы состоит из одной или нескольких бесконечно острых линий c частотами w_a , a восприимчивость c"(w) может быть записана в форме

c¢¢(w) = S A_ad(w-w_a); (15)

при этом функция релаксации G(t), пропорциональная фурье-преобразованию c¢¢(w), имеет вид

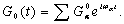(15a)

Если существует возмущение ħeH₁, то функция релаксации принимает вид G(e, t) и может быть в принципе вычислена вплоть до любого порядка по e методом возмущений; восприимчивость c¢¢(w, e) получается как фурье-преобразование G(e, t).

Прежде чем производить детальный расчет, кратко рассмотрим соотнношение между c¢¢(w) аи поведением намагниченности после окончания действия радиочастотного импульса. Хорошо известно и достаточно оченвидно, что для линейных систем стационарная реакция на возбуждение coswt представляется фурье-преобразованием нестационарной реакции на бесконечно острый импульс d(t). Однако на практике для аппроксиманции такого импульса к системе спинов необходимо приложить кратковренменно действующее магнитное поле, значительно большее постоянного поля Н_о.

Для системы взаимодействующих ядерных спинов в магнитном поле, характеризующейся острой резонансной линией на частоте w₀, действие бесконечно острого импульса постоянного поля можно аппроксимировать радиочастотным импульсом частоты w = w₀ со значительно большей длительностью t и меньшей амплитудой H₁. Поскольку в системе координат, вращающейся с частотой w, отлично от нуля только постоянное поле H₁, то для аппроксимации бесконечно острого импульса конечной амплитуды достаточно того, чтобы H₁ было значительно больше локального поля; последнее представляет собой гораздо менее жесткое условие.

Б. ШИРЕНИЕ, ВЫЗВАННОЕ ВЗАИМОДЕЙСТВИЕМ

МЕЖДУ ОДИНАКОВЫМИ СПИНАМИ

з 3. ДИПОЛЬ-ДИПОЛЬНОЕ ВЗАИМОДЕЙСТВИЕ

Полный гамильтониан системы одинаковых взаимодействующих спиннов в сильном внешнем поле может быть записан в виде

ħH = ħ(H₀ + H₁). (16)

Основной гамильтониан

ħH₀ = S_j Z^j = - għH₀ S_j I^j_z (16a)

описывает энергетические ровни, определяемые выражениема ħE⁰_M = - għН₀M, где M - собственное значение оператора

I_z = S_j I^j_zа

Гамильтониан возмущения ħ H₁, ответственный за ширение, имеет вид

а(16б)

Прежде всего, рассмотрим несколько подробнее взаимодействие между двумя спинами, которые будем обозначать для краткости i и iТ. Пусть q и j - полярные координаты вектора r, описывающего их взаимное положение, причем ось z направлена параллельно внешнему полю. Тогда W_ii можно записать в виде

W_ii'а = а{i×i' - 3[i_z cos q + sin q (i_x cos j + i_y sin j)]x[i'_z cos q + sin q (i'_x cos y + +i'_ysinj)]}g²ħ²/r³ = {i×i' - 3[i_z cos q + sin q (i₊ e^{- ij} + i_- e^ij)/2]x[i'_z cos q + sin q (i₊e^{- ij}+ + i_-e^ij)/2)]}g²ħ²/r³ = (A+B+C+D+E+F)g²ħ²/r³, (17)

где

A = i'_zi_z (l - 3cos² q),

B = - (l - 3cos² q) (i₊i'_Ц + i _Цi'₊) = (l - 3cos² q)(i_zi'_z - i×i')/2,

C = - 3sinq cosq e^{- ij} (i_zi'₊ + i ₊i'_z)/2, (18)

D = С* = - 3sinq cosq e ^ij (i_zi'_Ц + i _Цi'_z)/2,

E = - 3sin² q e^{-2 ij} i₊i'₊ /4,

F = E* = - 3sin² q e^{-2 ij} i _- i'_Ц /4,.

Запись W в такой форме вызвана следующими причинами. Согласно формуле (14),

c¢¢(w) ~ S¢ |< п | M_x | nТ >|².

Это приводит к необходимости определить изменение в положении энернгетических ровней, отвечающих ħH₀ , обусловленное наличием ħH₁. Операторы А, В, С, D, E, F дают качественно различным вклады в это изменение. помянутые операторы, действуя на состояние невозмущенного гамильтониана, характеризующееся значениями i_z=т, i'_z=т', принводят к следующему изменению этого состояния:

(19)

Рассмотрим теперь энергетический ровень ħE⁰_M = - għH₀M, соотнветствующий гамильтониану (16a). Этот ровень сильно вырожден, так как существует много способов, которыми можно скомбинировать отдельные значения I^j_z=m_j, чтобы получить величину M = S m_j. Таким образом, ровень ħE⁰_M соответствует вырожденному множеству состояний |М>, причем вырождение снимается (по крайней мере частично) возмущением, описываемым гамильтонианом ħH₁, который расщепляет ровень ħE⁰_M на много подуровней. Согласно первому приближению теонрии возмущений, вклад первого порядка в расщепление ровня ħE⁰_M дают лишь те члены гамильтониана возмущения, которые обладают отличнными от нуля матричными элементами внутри множества |М>, т. е. те, которые, действуя на состояние |М>, не вызывают изменения величины М. Обращаясь к формуле (19), мы видим, что только те части W, которые отвечают операторам А и В, удовлетворяют этому словию и должны быть сохранены для вычисления энергетических ровней ħH аметодом возмунщений.

Член А имеет тот же вид, что и выражение для взаимодействия двух классических диполей и описывает помянутое в разделе А взаимодействие одного диполя со статическим локальным полем, создаваемым другим дипонлем. Член В описывает взаимодействие, при котором возможно одновренменное переворачивание двух соседних спинов в противоположных направнлениях. Эта часть гамильтониана, названная переворачивающей частью, соответствует описанному в разделе А резонансному действию вращанющегося локального поля. Влияние такого члена, как С, заключается в примешивании к состоянию |М> с невозмущенной энергией ħE⁰_M = - għH₀M малой доли состояния |МЧ1>. Таким образом, точное собнственное состояние ħH₀ следует представить в виде

| М > + a | М - 1 > + Е,

где a - малая величина. Взаимодействие системы спинов с радиочастотнным полем, приложенным вдоль оси ох, пропорционально I_x = SI^j_x и может индуцировать только переходы с DМ = 1. Слабые переходы знежду состоянием, скажем, |M - 2> + малая примесь, энергия которого приблизительно равна - għH₀(M Ч2), и состоянием | М > + a | М - 1 > + Е становятся возможными с вероятностью порядка a². Разность энергии между этими состояниями приблизительно равна 2ħw₀. Следовательно, таким переходам на частоте 2w₀ соответствует очень слабая линия, котонрую обычно трудно наблюдать экспериментально. Легко видеть, что линии сравнимых интенсивностей появляются на частотах 0 и 3w₀.

Доказательство справедливости сохранения в гамильтониане ħH₁ только членов А и В, которые коммутируют с H₀ обычно называются адиабатической или секулярной частью ħH₁ и которые впредь будут обонзначаться как ħHТ₀, может быть также дано следующим способом. Так как c¢¢(w) пропорционально фурье-преобразованию G(t)=Sp{M_x(t)M_x}, то оно может быть вычислено, если известно M_x(t) = е^iHtM_xе^ЦiHt. В этом случае M_x(t) удовлетворяет равнению

(1/i) dM/dt = [H₀ +H₁, M_x(t)]. (20)

з 4. ОПРЕДЕЛЕНИЕ МОМЕНТОВ

Для резонансной кривой, описываемой нормированной функцией формы f(w) с максимумом на частоте w₀, n-й момент M_n относительно w₀ опреденляется выражением

М_n = ∫ (w - w₀)ⁿf(w)dw.

Если f(w) симметрична относительно w₀, то все нечетные моменты равны нулю. Знание моментов дает некоторую информацию о форме резонансной кривой и, в частности, о скорости, с которой она спадает до нуля на крыльях вдали от w₀.

Достоинство метода моментов состоит в том, что моменты могут быть вычислены на основании общих принципов без определения собственных состояний общего гамильтониана ħH. Прежде чем останавливаться на вычислении моментов, рассмотрим два примера резонансных кривых разном формы. Гауссова кривая описывается нормированной функцией

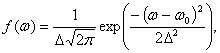(24)

для которой легко найти

М₂ = D², M₄ =3D⁴,

М_2n = 1, 3, 5,..., (2n - 1) D²ⁿ,

причем нечетные моменты равны нулю. Полуширина на половине высоты d определяемая соотношением f(w₀ + d) = f(w₀)/2, или ехр( - d²/2D²) = 1/2 оказывается равной

Отсюда видно, что значение второго момента M₂ = D² для гауссовой кринвой обеспечивает довлетворительное приближение для ширины линии d.

Другой формой линии, которая часто наблюдается в магнитном резоннансе, является лоренцева форма, опинсываемая нормированной функцией

а(25)

где d - полуширина на половине высоты.

В этом случае ни второй, ни более высокие моменты не могут быть определены, так как соответствующие интегралы расходятся. Однако иногда теория дает конечные значения для второго и четвертого моментов линий, которые в экспериментально наблюдаемой области имеют лоренцеву форму. В соответствии с конечными значениями M₂ и М₄ далеко на крыльях линии, где невозможно произвести достаточно точные измерения поглонщения вследствие его малой величины, линия должна изменяться более быстро, чем это следует из лоренцевой формы.

Грубая, но добная пробная модель состоит в описании кривой по формуле (25) внутри интервала |w - w₀|£a, где a>>d и в преднположении о том, что она равна нулю вне этого интервала. Тогда, прененбрегая членами порядка d/a, найдем

M₂ = D² = 2ad /p, M₄ = 2a³d /(3p), (IV.25a)

откуда, если известны M₂ и M₄ можно вычислить d и a. Поскольку

M₄ /( M₂)² = pa /6d,

упомянутая модель может быть использована лишь, когда теоретическое отношение M₄ /( M₂)² аоказывается большим числом., В этом случае

(IV.25б)

Ширина на половине высоты значительно меньше, чем среднеквадратичная ширина. С другой стороны, предположение о гауссовой форме линии может быть разумным всякий раз, когда отношение M₄ /( M₂)² апорядка 3.

з 5. МЕТОД ВЫЧИСЛЕНИЯ МОМЕНТОВ

Основной недостаток метода моментов состоит в том, что важный вклад в значение момента (вклад тем существеннее, чем выше момент) дают крылья кривой, которые на практике не наблюдаются. Необходимо из вычисленных моментов линии магнитного резонанса с центром на ларморовской частоте w =w₀ исключить вклады от сопутствующих линий на частотах w = 0, 2w₀, 3w₀ о которых упоминалось ранее. Легко видеть, что, несмотря на их малую интенсивность (благодаря даленности от центральной частоты w₀) вклад во второй момент сравним с вкладом от главной линии и тем больше, чем выше порядок момента. Для исключения вкладов от них следует рассматринвать в гамильтониане возмущения ħH₁ ответственного за ширение, только его секулярную часть ħH¢₀, которая коммутирует с H₀ и, следовантельно, не может отвечать перемешиванию состояний с различными полнными М; такое смешивание является причиной появления побочных линий. Таким образом, сокращение дипольного гамильтониана до его секулярной части

не только упрощает вычисление моментов, но и делает его более точным.

Прежде чем начать расчет, отметим, что линия магнитного резонанса симметрична относительно центральной частоты w₀. бедимся в правильнности этого тверждения. Если | > и | b > Ч два собственных состояния ħ(H₀+H¢₁) с разностью энергии ħ(Е_а - Е_b) = ħw₀ + d_ab, то два состоянния | а^~ > и | b^~ >, полученные из | > и | b > соответственно путем повонрота всех спинов в обратном направлении, будут также собственными состояниями ħ(H₀+H¢₁) с ħ(Е_b~ - Е_a~) = ħw₀ + d_ab. Таким образом, каждонму переходу с частотой w₀ + u соответствует переход равной интенсивности с частотой w₀ Ц u. Если f(w) - функция формы, то h (u) = f(w₀ + u)Ч четная функция u. Поскольку моменты кривой пропорциональны пронизводным в начале координат от их фурье-преобразования, мы будем применять для их вычисления формулу (13). Вследствие зости линии ядерного магнитного резонанса можно пренебречь изменением величины w в пределах ширины линии и предположить, что форма линии описывается c¢¢(w)/w, так же как и c¢¢(w). Тогда, поскольку f(w) - нормированная функция формы, (13) может быть переписано в виде

f(w) = A∫ G(t) cos wt dt, (IV.26)

где постоянная A определяется из словия нормировки f(w), опреденленная ранее четная функция G (t) равна Sp{M_x(t)M_x}. Обратно

G(t) = 2/(pA)∫ f(w) cos wt dw, (IV.27)

Согласно вышеизложенному, в выражении

M_x(t) = е^iHtM_xе^ЦiHt.

следует вместо H = H₀+H₁а подставить H = H₀+H¢₁а что значинтельно прощает вычисления. Поскольку H₀ и H¢₁а коммутируют, можно записать

exp{i(H₀+H¢₁)t} = exp(iH₀t) exp(iH¢₁t).

Учитывая, что зеемановский гамильтониан ħH₀ равен ħw₀I_z функцию G (t) можно переписать в виде

(IV.28)

Шпур произведения операторов инвариантен относительно циклической перестановки, поэтому

(IV.28a)

В этом выражении оператор exp(iw₀I_zt) определяет поворот на гол w₀t вокруг оси z, и, следовательно, можно записать

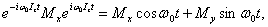
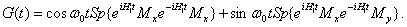а(29)

Легко видеть, что второй член в (29) равен нулю, так как поворот спинов на 180

Заменяя в (27) G (t) на G₁(t)cosw₀t, где

G₁(t)=Sp{еxp(iHС₁t)M_xе(ЦiHС₁t)M_x}

называется сокращенной функцией автокорреляции, и вводя обозначение

h (u) = f(w₀ + u),

получаем

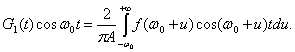
Заменяя нижний предел на - ¥, что допустимо для зких линий, найдем

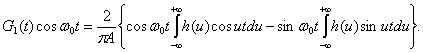
Поскольку h (и) является четной функцией, второй интеграл равен нулю и

G₁(t)=Sp{еxp(iHС₁t)M_xе(ЦiHС₁t)M_x}

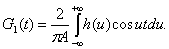(30)

Различные моменты кривой распределения h (и) относительно резонансной частоты w =w₀ определяются выражением

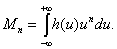
Нечетные моменты равны нулю, четные определяются формулой

(31)

Таким образом, для вычисления моментов резонансной кривой достаточно разложить G₁ (t) в выражении (30) по степеням t. При этом коэффициенты разложения представляют собой шпуры от операторов, которые являются полиномами от H¢₁ и M_x.

Сущность метода заключается в том, что значения помянутых шпуров не зависят от выбора основных состояний и могут быть вычислены, напринмер, в представлении, где значения m^j = I^j_z аотдельных спинов (поэтому представление называется m^j-представлением) являются хорошими кваннтовыми числами. Таким образом, нет необходимости решать проблему отыскания собственных состояний | n > полного гамильтониана. Из опренделения (30) функции G₁(t) вытекает, что значение ее р-й произнводной в момент t = 0 определяется выражением

а(IV.32)

Формула (32) просто находится из дифференциального равнения

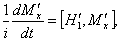(33)

которому удовлетворяет зависящий от времени оператор

M¢_x(t) = е(iH₁¢t)M_xе(ЦiH₁¢t)^t.

Решение этого уравнения может быть представлено в виде ряда

M¢_x(t) = M_x + M¢ ⁽¹⁾_x(t) + M¢ ⁽²⁾_x(t) + Е+ M¢ ⁽ⁿ⁾_x(t),

отдельные члены, которого получаются методом индукции с помощью соотнношения

из последнего сразу же следует (32). Из (31) и (32) для первых двух четных моментов находим

(34)

(34a)

B (34) M_x заменено полным спином I_x, пропорциональным M_x. Понскольку мы определили гамильтониан в виде ħH, следует помнить, что эти моменты соответствуют ширинам линии, измеренным в единицах w = 2pn.