Читайте данную работу прямо на сайте или скачайте
Механические колебания в дифференциальных равнениях
Министерство образования Российской Федерации
Магнитогорский государственный технический ниверситет им. Г.И. Носова
РЕФЕРАТ
на тему:
УМЕХАНИЧЕСКИЕ КОЛЕБАНИЯ В ДИФФЕРЕНЦИАЛЬНЫХ РАВНЕНИЯХФ
Выполнил: студент гр. МХТ-02
Казаков Василий Васильевич
Проверила:
Абрамова Ирина Михайловна
Магнитогорск 2003
Содержание
1) Гармонические колебания
2) Затухающие колебания
3) Вынужденные колебания без чета сопротивления среды
4) Вынужденные колебания с четом сопротивления среды
Колебаниями называются процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качания маятника часов, переменный электрический ток и т.д. При колебательном движении маятника изменяется координата центра масс, в случае переменного тока колеблются напряжение и сила тока. Физическая природа колебаний может быть разной, однако различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми равнениями. Рассмотрим механические колебания.
Гармонические колебания.
Гармоническими колебаниями называются колебания, при которых изменяющаяся величина изменяется по закону синуса (косинуса).
Пусть груз весомподвешен на вертикальной пружине, длина которой в естественном состоянии равна 
|
М |
|
Р |
|
х |
|
l |
|
lст |
|
х |
|
О |
 Решение
Решение
Направим ось Ох вниз по вертикальной прямой, проходящей через точку подвеса груза. Начало координат О выберем в положении равновесии груз, то есть в точке, в которой вес груза уравновешивается силой натяжения пружины.
|
О |
 Пусть l означает длинение пружины ав данный момент, lстЧстатическое длинение, т.е.
расстояние от конца нерастянутой пружины до положения равновесия. Тогда l=lст+х, или l-lст=х.
Пусть l означает длинение пружины ав данный момент, lстЧстатическое длинение, т.е.
расстояние от конца нерастянутой пружины до положения равновесия. Тогда l=lст+х, или l-lст=х.
Дифференциальное равнение получим из второго закона Ньютона: F=ma, где m=P/gЧмасса груза Чускорение движения и FЧравнодей-ствующая приложенных к грузу сил. В данном случае равнодействующая слагается из силы натяжения пружины и силы тяжести.
По закону Гука сила натяжения пружины пропорциональна её длинению: Fупр=-сl, где с - постоянный коэффициент пропорциональности называемый жесткостью пружины.
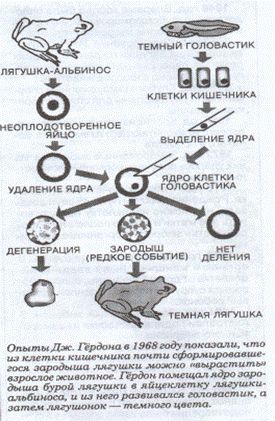
Так как в положении равновесия сила равновесия сила натяжения пружины равновешивается весом тела, то P= сlст. Подставим в дифференциальное уравнение выражениеи заменим аl-lст через х, получится равнение в виде:
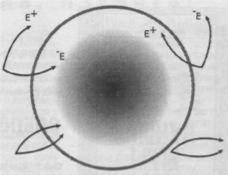
или, обозначив с/m через k2,
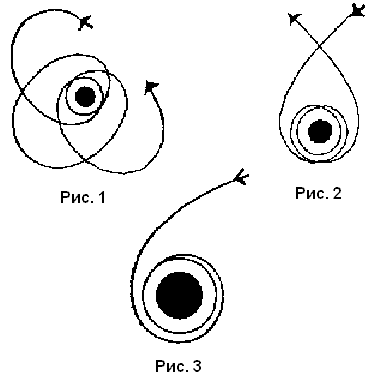 (1)
(1)
Полученное равнение определяет так называемые свободные колебания груза. Оно называется равнением гармонического осциллятора. Это линейное дифференциальное равнение второго порядка с постоянными коэффициентами. Его характеристическое равнение:
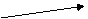
имеет мнимые корни 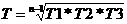 ,
соответственно этому общее решение
,
соответственно этому общее решение
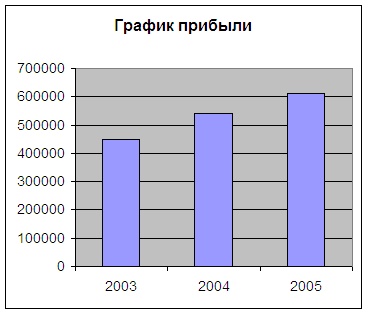
Для выяснения физического смысла решения добнее привести его к другой форме, введя новые произвольные постоянные.
Умножив и разделив на 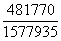
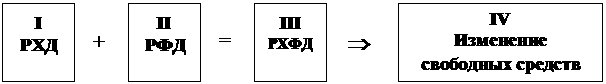
Если положить
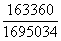 а
а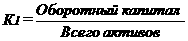 а
а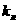
то
 (2)
(2)
График гармонических колебаний имеет вид:
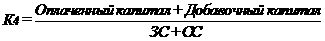
Таким образом, груз совершает гармонические колебания около положения равновесия.
Величину А называют амплитудой колебания,
а аргунмент 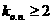 Ч фазой колебания. Значение фазы при t=o т.e. авеличина а
Ч фазой колебания. Значение фазы при t=o т.e. авеличина а ,
называется начальной фазой колебания.
Величина
,
называется начальной фазой колебания.
Величина 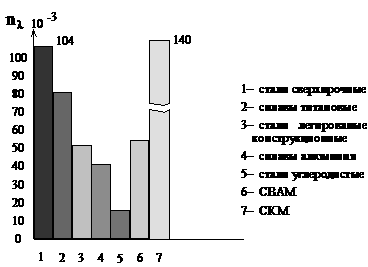 аесть частота колебания. Период коленбания
аесть частота колебания. Период коленбания  и частота k зависят только от жесткости пружины и от массы системы. Так как с = Р/lст = mg/lст,
то для периода можно получить также формулу:
и частота k зависят только от жесткости пружины и от массы системы. Так как с = Р/lст = mg/lст,
то для периода можно получить также формулу:
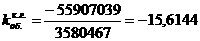
Скорость движения груза получается дифференцированнием решения по t:

Для определения амплитуды и начальной фазы необхондимо задать начальные словия. Пусть, например, в начальнный момент t = 0 положение груза x=x0 и скорость u=u0. Тогда 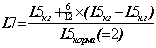 а
а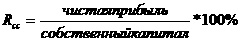 ,
откуда
,
откуда
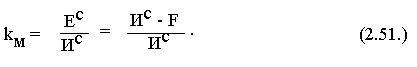 ,
, 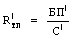
Из формул для амплитуды и начальной фазы видно, что в отличие от частоты и периода собственных коленбаний они зависят от начального состояния системы. При отсутствии начальной скорости (u0=0) амплитуда А=х0, начальная фаза a=p/2 и, таким образом,
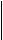 а или
а или 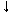
Затухающие колебания.
Затухающими колебаниями называются колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени меньшают-ся. Найдем закон движения груза в словиях предыдущей задачи, но с четом сопротивления воздуха, которое пропорционально скорости движения.
Решение
К силам, действующим на груз, прибавнляется здесь сила сопротивления воздуха 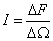 а(знак минус показывает,
что сила R направлена противопонложно скорости u).
Тогда дифференциальное уравнение движения в проекции на ось Ox имеет вид
а(знак минус показывает,
что сила R направлена противопонложно скорости u).
Тогда дифференциальное уравнение движения в проекции на ось Ox имеет вид

или если положить 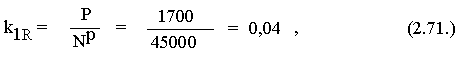
 (3)
(3)
Это равнение также является линейным однородным уравнением второго порядка с постоянными коэффициеннтами. Его характеристическое равнение:
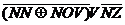
имеет корни
 (4)
(4)
Характер движения целиком определяется этими корннями.
Возможны три различных случая. Рассмотрим снанчала случай, когда 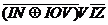 .
Это неравенство имеет место, когда сопротивление среды невелико. Если полонжить
.
Это неравенство имеет место, когда сопротивление среды невелико. Если полонжить
 ,
то корни (4) имеют вид
,
то корни (4) имеют вид 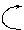
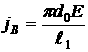
или, преобразовав, множая и деля на 
положим, что
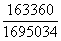 а
а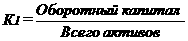 а
а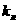
тогда
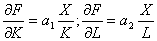 (5)
(5)
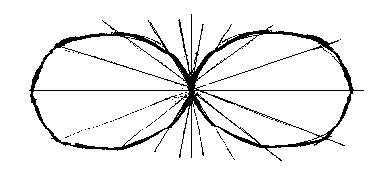
График зависимости отклонения от положения равновесия от времени имеет вид:
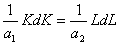
Если заданы начальные словия: 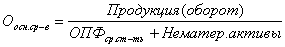 апри t = 0, то можно определить А и a. Для этого находим
апри t = 0, то можно определить А и a. Для этого находим

и подставляема t
= 0а ва выражения для 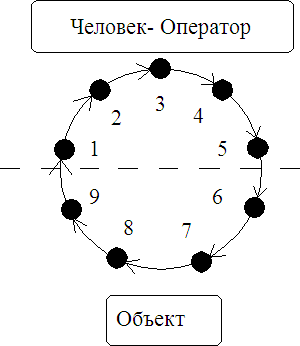
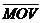 аполучим систему уравнений
аполучим систему уравнений
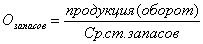
Разделелив обе части второго равнения на соответствующие части первого получим

откуда
 или
или 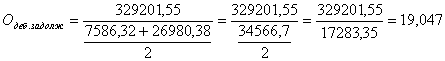
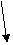
Так как
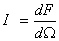
то
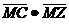
Решение (5) показывает, что имеют место затухающие колебания. Действии-тельно, амплитуда колебания  азавинсит от времени и является монотонно убывающей функцией, причем
азавинсит от времени и является монотонно убывающей функцией, причем  апри
апри  .
.
Период затухающих колебаний определяется по формуле

Моменты времени, в которые груз получает максимальнное отклонение от начала координат (положения равновенсия), образуют арифметическую прогрессию с разностью, равной полупериоду Т/2. Амплитуды затухающих коленбаний образуют бывающую геометрическую прогрессию со знаменателем, равным 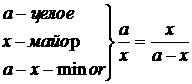 аили
аили 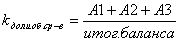 .
Эта величина называется декрементом затухания и обычно обозначается буквой D. Натуральный логарифм декремента lnD = - пТ/2 называется логарифмическим декрементом затухания.
.
Эта величина называется декрементом затухания и обычно обозначается буквой D. Натуральный логарифм декремента lnD = - пТ/2 называется логарифмическим декрементом затухания.
Частота колебаний 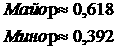 в этом случае меньше, нежели в предыдущем (
в этом случае меньше, нежели в предыдущем (
Если сопротивление среды велико и 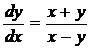 ,
то, положив
,
то, положив 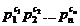 ,
получим корни (4) в виде
,
получим корни (4) в виде 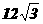 Так как
Так как 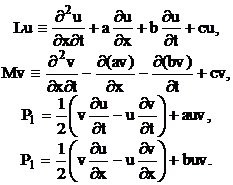
 (6)
(6)
Отсюда видно, что движение апериодическое и не имеет колебательного характера. Аналогичный характер будет иметь движение и в случае 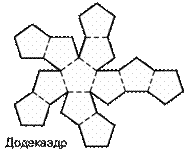 ,
когда общее решение имеет вид
,
когда общее решение имеет вид
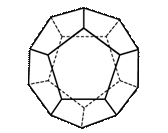 (7)
(7)
Легко заметить, что в обоиха последниха случаях при  аимеем
аимеем  .
.
Если заданы начальные словия 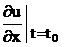 аи
аи 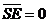 , то в случае, когда
, то в случае, когда 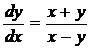 ,
имеем
,
имеем 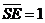

 аи
аи 

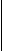
и, следовательно

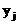
В случае же, когда  получаем
получаем 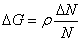
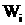 аи следовательно,
аи следовательно,

Вынужденные колебания без учета сопротивления среды.
Вынужденными колебаниями называют колебания, вызванные внешней периодической возмущающей силой.
Пусть груз весомподнвешен на вертикальной пружине, длина которой в ненангруженном состоянии равна  . На груз действует периондическая возмущающая сила
. На груз действует периондическая возмущающая сила 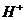 агде Q и р - постояые.
Найдем закон движения груза, пренебрегая массой пружины и сопротивлением среды.
агде Q и р - постояые.
Найдем закон движения груза, пренебрегая массой пружины и сопротивлением среды.
Решение
Как и для гармонических колебаний, получаем уравнение

Полагая, как и прежде, 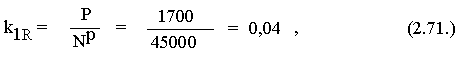 аи, кроме того,
аи, кроме того,  аперенпишем равнение в виде
аперенпишем равнение в виде
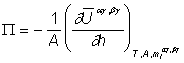 (8)
(8)
ЭтоЧнеоднородное линейное равнение второго порядка с постоянными коэффициентами, причем однородным равннением,
соответствующим равнению (8), является
(1). Поэтому 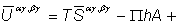 х. Если преднположить, что
х. Если преднположить, что 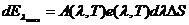 то частное решение х, нужно искать в виде
то частное решение х, нужно искать в виде 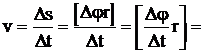 М и N - коэфнфициенты, подлежащие определению. Итак,
М и N - коэфнфициенты, подлежащие определению. Итак,
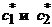
Производя вычисления, получаем
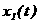
откуда М=0 и 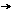 Полученное таким образом частное решение
Полученное таким образом частное решение
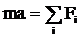 (9)
(9)
определяет так называемые вынужденные колебания,
созданные возмущаю-щей силой 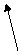 k>p,
либо отличаются на p, если k<p,
т. е. если N<0.
k>p,
либо отличаются на p, если k<p,
т. е. если N<0.
Закон движения представляется общим решением
 (10)
(10)
Оно слагается из собственно вынужденных колебаний (9), которые определяются внешней возмущающей силой, и собственных колебаний (2), обусловленных исключительно внутренними причинами: жесткостью пружины и массой груза.
Если заданы начальные словия: 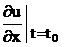 аи
аи 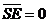 , то можно определить произвольные постоянные А и u. Для этого продифференцируем функцию (10):
, то можно определить произвольные постоянные А и u. Для этого продифференцируем функцию (10):

и подставима в выражения х и
 азначениеа аргумента t = 0; получима систему равненийа относительно
A и a:
азначениеа аргумента t = 0; получима систему равненийа относительно
A и a:

Преобразуем её так:
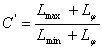
возведем в квадрат обе части каждого из этих уравнений и сложим. Тогда

Для нахождения a разделим обе части первого равннения на соответствую-щие части второго; получим
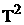
откуда

при этом 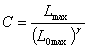 а а
а а
Итак, искомыма частным решением, довлетворяющим заданным начальным словиям, является функция
или

Частное решение (9), характеризующее собственно выннужденные колебания, было получено в предположении, что 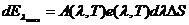
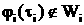
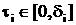 (11)
(11)
Частное решение следует искать в форме
 ,
,
где М и N - коэффициенты, подлежащие определению. Итак,
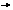
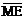
откуда получаем 
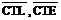

Общее решение в этом случае
 (12)
(12)
Найдем  и подставима ва выражения х и
и подставима ва выражения х и  значение t=0; получим
значение t=0; получим
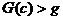

 или
или 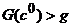
Из последних двух равенств находим
 а
а 
откуда

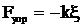

Перепишем общее решение так:
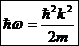
тогда искомоеа частное решение, довлетворяющее задаым начальным словиям, запишется в виде.
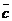
Выражение (12) показывает, что амплитуда вынуждеых колебаний  ав этом случае может стать неогранниченно большой даже тогда, когда q невелико. Иначе говоря, возможно получение сколь угодно больших амплинтуд при малых возмущающих силах. Это явление называется резонансом. Таким образом,
резонанс наступает тогда, когда частота возмущающей силы совпадает с частонтой собственных колебаний.
ав этом случае может стать неогранниченно большой даже тогда, когда q невелико. Иначе говоря, возможно получение сколь угодно больших амплинтуд при малых возмущающих силах. Это явление называется резонансом. Таким образом,
резонанс наступает тогда, когда частота возмущающей силы совпадает с частонтой собственных колебаний.
Впрочем, в действительности точное совпадение этих частот не является необходимым. Выражение (9) для вынужденного колебания показывает, что при близости частот амплитуда 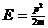 аможет быть очень большой, хотя и ограниченной при фиксированных частотах k и р. Возможностью создания колебаний с значительной амплинтудой часто пользуются в различных силителях,
например в радиотехнике. С другой стороны, в большом числе слунчаев появление больших амплитуд является вредным, ибо может приводить к разрушению конструкций
(скажем, мостов или перекрытий).
аможет быть очень большой, хотя и ограниченной при фиксированных частотах k и р. Возможностью создания колебаний с значительной амплинтудой часто пользуются в различных силителях,
например в радиотехнике. С другой стороны, в большом числе слунчаев появление больших амплитуд является вредным, ибо может приводить к разрушению конструкций
(скажем, мостов или перекрытий).
Вынужденные колебания с учентом сопротивления среды.
Найдем закон движенния груза в словиях предыдущей задачи с четом сопронтивления среды, пропорционального скорости движения.
Решение
Как и выше, имеем

или положив
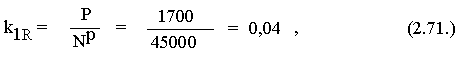

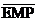 а (13)
а (13)
Однородным равнением, соответствующим (13),
является равнение (3) с корнями характеристического равнения (4).
Предположим, что сопротивление среды невелико, т. е. 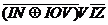 .
При этом общее решение однородного равннения имеет вид (5):
.
При этом общее решение однородного равннения имеет вид (5):

где 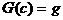 .
Это решение определяет свободные колебания, которые будут затухающими. Для отыскания вынужденных колебаний ищем частное решение в виде
.
Это решение определяет свободные колебания, которые будут затухающими. Для отыскания вынужденных колебаний ищем частное решение в виде
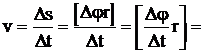
Имеем:
 а
а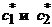
Сравнивая коэффициенты, получаем систему

Так как
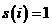 а
а 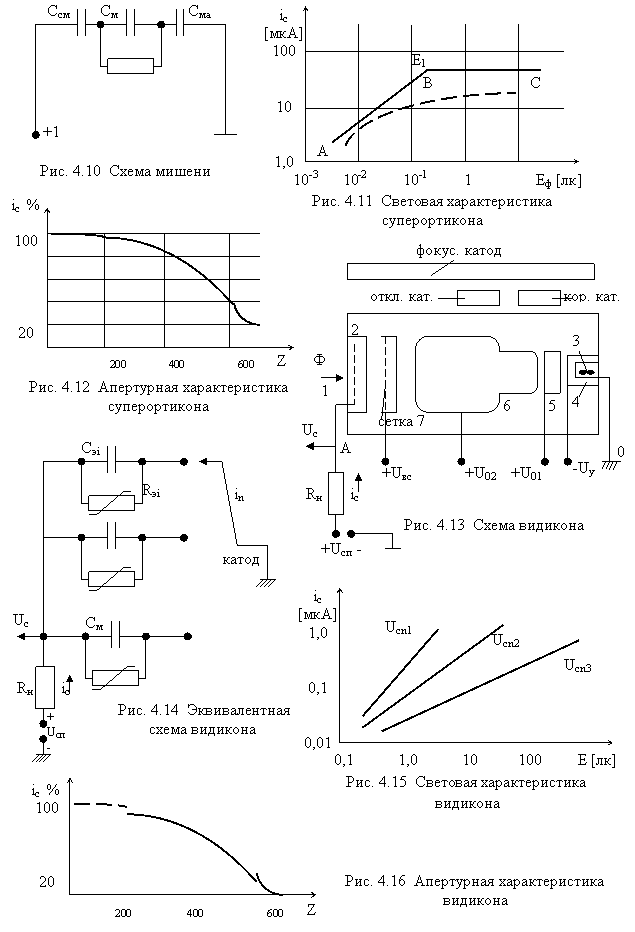

 а
а 
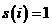 а
а


то
 аи
аи 
и мы находим частное решение
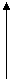
Преобразуем выражение 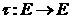 аследующим образом:
аследующим образом:
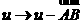
Обозначив
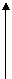
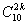
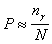 (14)
(14)
перепишем 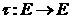 авиде
авиде
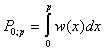 (15)
(15)
Выражение
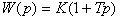 (16)
(16)
носит название сдвига фазы. Общее решение, как и в прендыдущей задаче, слагается из свободных колебаний [см. формулу (5)] и собственно вынужденных колебаний (15):
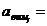 (17)
(17)
Первое слагаемое, как было сказано выше,
определяет затухающие колебания, которые, особенно при большом  Q
периодического возмущения, так как
Q
периодического возмущения, так как  . Она отлинчается от q множителем
. Она отлинчается от q множителем
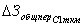 (18)
(18)
характеризующима зависимость амплитуды вынужденного колебания от частоты возмущающей силы.
Определим максимум этой амплитуды. Для этого найндем производную функции (18)

Положив  , получим равнение
, получим равнение 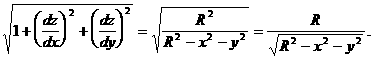 а(случай р = 0а отбрасывается кака невозможный), корень которого дает частоту внешних сил:
а(случай р = 0а отбрасывается кака невозможный), корень которого дает частоту внешних сил:

при которой, как показывает проверка достаточных условий экстремума, амплитуда вынужденных колебаний будет максимальной. Максимальное значение амплитуды равно
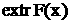 (19)
(19)
Формула (19) показывает, что амплитуда колебаний тем больше, чем меньше п. При малых п частота р близка к частоте собственных колебаний k.
Решение а(15) существует всегда, когда
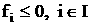
В случае 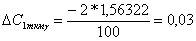 получаем
p=k и n= 0, и равнение (13)
превращается в равнение (11). Здесь вновь наступает явление резонанса, при котором, как было рассмотрено выше, вынужденные колебания имеют вид (12).
получаем
p=k и n= 0, и равнение (13)
превращается в равнение (11). Здесь вновь наступает явление резонанса, при котором, как было рассмотрено выше, вынужденные колебания имеют вид (12).

