Читайте данную работу прямо на сайте или скачайте
Матриц та системи нйних рвнянь (матрица системных линейных равнений)
ДРОГОБИЦЬКИЙ ДЕРЖАВНИЙ ПЕДАГОГ
ЧНИЙ УН
ВЕРСИТЕТ
МЕН
ВАНА ФРАНКА
О.Л.ГОРБАЧУК, Л.
.КОМАРНИЦЬКА, Ю.П.МАТУР
Н
МАТРИЦ
ТА СИСТЕМИ Л
Н
ЙНИХ Р
ВНЯНЬ
НАВЧАЛЬНО-МЕТОДИЧНИЙ ПОС
БНИК
Дрогобич - 2007
УДК 512.64(09)
К 63
Матриц та системи нйних рвнянь: Навчально-методичний посбник / Горбачук О.Л., Комарницька Л.
., Матурн Ю.П. - Дрогобич: Редакцйно-видавничий вддл ДДПУ, 2007. - 50 с.
Посбник написано вдповдно до програми навчально
Розрахований на студентв-математикв, як вивчають курс алгебри в педагогчних та класичних нверситетах, на вчителв математики та старшокласникв, як цкавляться математикою.
Бблографя 5 назв.
Рекомендовано до друку Вченою радою Дрогобицького державного педагогчного нверситету мен
вана Франка
(протокола № 8а вда 29 червня 2007 р.)
Вдповдальний за випуск:а доцент Галь Ю.М.
Редактор:а Невмержицька
рина Михайлвна
Рецензенти:
Пташник Б.Й., доктор фзико-математичних наук, професор, член-кореспондент НАН кра
Зарчний М.М., доктор фзико-математичних наук, професор, декан механко-математичного факультету Льввського нацонального нверситету мен
вана Франка.
й Горбачук О.Л.,
Комарницька Л.
.,
Матурн Ю.П.
ЗМ
СТ
Вступ.4
1. Матриц та дÿ над ними.........................................................................5
Означення матриць 5
Види матриць..5
Означення дй над матрицями ..8
1.4. Властивост додавання матриць
та множення матриць на числа 10
1.5. Символ суми...11
1.6. Властивост множення матриць..12
1.7. Властивост транспонування...14
1.8. Обернена матриця у випадку квадратних матриць
адругого порядку. 15
1.9. Приклади матриць, елементами яких
вектори.18
1.10. Числовий n-вимрний простр.. 20
1.11. Подбн матриц. 21
1.12. Вправи 21
2. Системи нйних рвнянь23
2.1. Система двох нйних рвнянь з двома невдомими 23
2.2. Системи нйних рвнянь: основн означення 25
2.3. Елементарн перетворення системи нйних рвнянь.. 27
2.4. Схдчаст системи 30
2.5. Зведення системи нйних рвнянь до схдчастого вигляду
(Метод Гаусса).. 33
2.6. Вправи.. 36а
3. Жорданова форма матриць та матричн рвняння37
3.1. Слд квадратно
3.2. Жорданова форма квадратних матриць. Основна теоремЕ. а38
3.3. Зведення до жорданово
3.4. Власн значення власн вектори квадратно
3.5. Зведення квадратно
3.6. Загальний випадок43
3.7. Однозначнсть визначення жорданово
3.8. Спектр квадратно
3.9.
Рвняння  а
а
3.10. Вправи49
Список тератури. 50
Вступ
Метою даного навчального посбника
ознайомлення читач з елементами теорÿ матриць та систем нйних рвнянь. Цей матерал
доступним не лише для студентв-першокурсникв, але й для старшокласникв. а
Серед розглядуваних питань найважлившими
властивост дй над матрицями, рвносильн перетворення систем лнйних рвнянь, жорданова форма матриць та матричн рвняння. Останн питання мають поглибити знання студентв в галуз теорÿ матриць, користуючись при цьому тльки елементарними засобами.
Кожний з роздлв закнчу
ться вправами, як люструють й доповнюють теоретичний матерал.
Теоря матриць вдгра
важливу роль не тльки у всх галузях математики, але й ау фзиц. Тому ? вивчення повинно бути дуже ретельним. Матриц з числовими елементами
природнм загальненням чисел широко використовуються в алгебр, як приклади алгебра
РозвТязування систем нйних рвнянь методом Гаусса фактично зводиться до певних перетворень над
Вивчення теми про жорданову форму матриць дозволить досить просто розвТязувати деяк типи матричних рвнянь.
Джерела з списку тератури допоможуть зацкавленим студентам продовжити вивчення тем, викладених у посбнику.
Роздл 1. Матриц та дÿ над ними
1.1. Означення матриць
Матрицею назива
ться прямокутна таблиця, що заповнена певними математичними обТ
ктами, як називаються елементами матриц. Тут будемо розглядати лише так матриц, елементами яких
числа. Елементи матриц будемо позначати однúю буквою з двома ндексами, де перший ндекс вказу
номер рядка елемента матриц, а другий нЦ номер його стовпця.
Таким чином, матриця запису
ться у форм:

 або
або 





Якщо матриця ма
k рядкв n стовпцв, то про таку матрицю кажуть, що вона ма
розмр k × n.
Якщо кльксть рядкв кльксть стовпцв матриц рвн, то така матриця назива
ться квадратною, кльксть ? рядкв (стовпцв) назива
ться ? порядком.
Матрицю також позначають великими латинськими терами або за допомогою вдповдних малих тер з двома ндексами:
=  а=а
а=а  В =
В =  а=
а= 
Дв матриц однакових розмрв називають рвними, якщо
Наприклад, матриц
A =  В =
В = 
не
рвними ( А ≠
В ), оскльки 
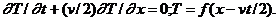
1.2. Види матриць
Матриця, що склада
ться з одного рядка [стовпця], назива
ться матрицею-рядкома [матрицею-стовпцем].
Матрицю-рядок також називають рядком, матрицю-стовпець - стовпцем. Використовуються також наступн термни: вектор-рядок, вектор-стовпець. Вектор, що склада
ться з n елементв, назива
ться n-вимрним.
Матриця О довльних розмрв, вс елементи яко
О = 
Рядок [стовпець], вс елементи якого
нул, назива
ться нульовим рядком [стовпцем] або нуль-вектором.
Одиничною матрицею назива
ться квадратна матриця Е n-го порядку наступного вигляду:
Е = 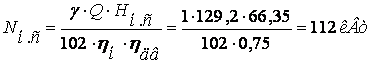 а= [
а= [ ij],
ij],
де  ij =
ij =  Ц символ Кронекера.
Ц символ Кронекера.
Квадратна матриця D назива
ться дагональною, якщо вона ма
наступний вигляд:
тобто dij = 0, якщо ¹ j. Таку матрицю також позначають наступним чином:
D = diag  .
.
Наприклад, 
Квадратна матриця А назива
ться нижньою трикутною, якщо вона ма
вигляд:
А = ,
,
тобто аij = 0, якщо < j.
Квадратна матриця А назива
ться верхньою трикутною, якщо вона ма
вигляд: 

=  ,
,
тобто аij = 0, якщо > j.
Матриця, яка
або нуль-матрицею, або матрицею виду
 а,
а,
де  а0,
а0,  а0,...,
а0,...,  0
називають верхньою трапецúподбною матрицею.
0
називають верхньою трапецúподбною матрицею.
Приклади:
1).  а нуль-матриця;
а нуль-матриця;
2). 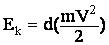 а―
вектор-стовпець;
а―
вектор-стовпець;
3).  а― дагональна матриця;
а― дагональна матриця;
4).  а― одинична матриця;
а― одинична матриця;
5).  а― нижня трикутна матриця;
а― нижня трикутна матриця;
6). 
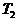
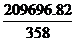
 а― верхн трапецúподбн матриц.
а― верхн трапецúподбн матриц.
Схдчастою називають матрицю А, яка ма
наступн властивост:
1). Якщо -ий рядок нульовий, то (ί+1)-ийа рядок також нульовий;
2). Якщо перш ненульов елементи ί-го (ί+1)-го рядкв
в стовпцях К К+1 вдповдно, то К < К+1.
Приклад.
 а― схдчаста матриця, де
а― схдчаста матриця, де 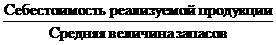


1.3. Означення дй над матрицями
Сумою двох матриць однакових розмрв А В називають матрицю С, кожний елемент яко
С=А+В=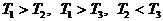
(або 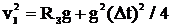 адля всх i, аj).
адля всх i, аj).
Добутком матриц А на число λ називають таку матрицю В, кожний елемент яко
В =
λ А = λ  а=
а=  а=
а= 
(або  адля всх
адля всх 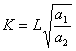
Матрицю (-1) А позначатимемо через ЦА називатимемо ? матрицею, протилежною до матриц А.
Пд рзницею матриць А В (А - В) будемо розумти суму А + (-В). Зрозумло, що А - А = О, А + О = О +А = А для всяко
Транспонованою до матриц А розмрв k аn назива
аn назива
ться така матриця Ва розмрв n  аk, що
аk, що
 адля всх,
j. Тобто матриця В ма
адля всх,
j. Тобто матриця В ма
за рядки вдповдн стовпц матриц А.
Транспоновану матрицю позначають через АT, елементи ? через 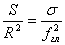 ( = а
( = а ).
).
Приклад:
= 
 T=
T= 
Для введення добутку двох матриць визначимо спочатку добуток рядка стовпця однаково
 а
а а=
а= 
У результат одержимо квадратну матрицю першого порядку, яку можна ототожнити з ?
диним елементом  Добуток АВ матриць А В визнача
Добуток АВ матриць А В визнача
мо тльки тод, коли кльксть стовпцв матриц А дорвню
клькост рядкв матриц В.
Нехай матриця А ма
розмр  В - n
В - n .
.
Добутком матриць А В назива
ться матриця С = АВ, що ма
розмр k r, ? елемент
r, ? елемент  адорвню
адорвню
добутку -го рядка матриц А j-го стовпця матриц В:
cij = 

 а=
а= 
i =1,..., k; j =1, ..., r.
Приклади:
1).  а
а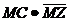 а=
а= 
2). 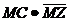 а
а а
а
3).  а
а а=
а= 
4).  а
а
Нехай А - квадратна матриця n-го порядку, Е - одинична матриця n-го порядку, О - квадратна нуль-матриця n-го порядку. Тод легко переврити, що:
Е = е = А,
О = ОА = О.
Слд зауважити, що добуток двох ненульових матриць може бути нульовою матрицею (нуль-матрицею).
Справд,  а
а
Квадратна матриця В n-го порядку назива
ться оберненою до квадратно
В = ВА = Е.
Обернену матрицю до матриц А позначають через 
Приклад.
Нехай А =  В =
В =  Ц обернена матриця до матриц А.
Ц обернена матриця до матриц А.
1.4. Властивост додавання матриць та множення матриць на числа
Додавання матриць та множення матриць на числа мають наступн властивост:
1. А + (В + С) = (А + В) + С (асоцативнсть);
2. + О = О + А = А;
3. + (-А) = (-А) + А = О;
4. А + В = В + А (комутативнсть);
5.
 А;
А;
6.
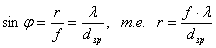 А + В) =
А + В) = 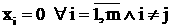 А +
А + 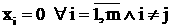 В;
В;
7.
(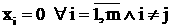 а+
а+  А =
А = 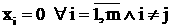 А +
А +  А;
А;
8.
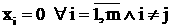
 А) = (
А) = ( А
А а
а
(для довльних матриць А, В, С однакових розмрв для довльних чисел 

Доведемо властивост 1 7. Вс нш властивост доводяться аналогчно залишаються для самостйного доведення читачу.
1. А + (В + С) =  а+
а+ 

=  =
=
= 
(тут ми використали асоцативнсть додавання чисел).
7. 
=
(тут ми використали дистрибутивнсть множення вдносно додавання для чисел).
1.5. Символи суми
Суму  апозначають через
апозначають через
 назива
назива
ться ндексом пдсумовування його позначення рол не вдгра
, тобто його можна замнити будь-якою ншою буквою:
1). 
Очевидними також
й нш властивост символу суми:
2).  а(адитивнсть);
а(адитивнсть);
3).  а(однорднсть);
а(однорднсть);
де  Ц будь-яке число (яке не залежить вд ).
Ц будь-яке число (яке не залежить вд ).
Часто використовуються так зван подвйн суми, як необхдн для пдсумовування доданкв з двома ндексами.
 а
а
тобто для знаходження суми всх елементв прямокутно

Тут, j називаються першим другим ндексами пдсумовування вдповдно.
Очевидно, що сума S всх елементв дано
S = 
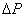
 а
а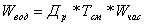
де 
Тому 
(Знаходимо суму всх сум елементв рядкв).
З другого боку,
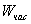

(Знаходимо суму всх сум елементв стовпцв).
Таким чином, ма
мсце наступна властивсть символу подвйно
4). 
Взагал кажучи, символ суми може записуватися у найрзномантнших ситуацях. Його ж змст може бути зрозумлим з контексту.
Тепер нам легко буде оперувати з матрицями. Наприклад, елемент добутку  аматриць
аматриць  а
а 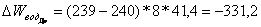 арозмрв
арозмрв 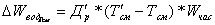 а
а 

1.6. Властивост множення матриць
1. Множення матриць не
комутативним, тобто снують так матриц А В, для яких АВ ≠ ВА.
Наприклад,
 а
а
2. (АВ)С = А(ВС) для довльних матриць А, В, С, для яких снують добутки АВ ВС (асоцативнсть).
Справд, нехай А ма
розмр  Покладемо АВ = U
ВС = V. Зрозумло, що U ма
Покладемо АВ = U
ВС = V. Зрозумло, що U ма
розмр 
 UС = АV. Доведемо це.
UС = АV. Доведемо це.
Елемент добутку UС дорвню

ле 
 UС
(використана властивсть 3 символу суми).
UС
(використана властивсть 3 символу суми).
Знайдемо тепер елемент добутку АV.

(використана властивсть 3 символу суми).
Використавши властивсть 4 подвйних сум, матимемо, що UС = АV.
3. 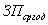 аякщо
аякщо 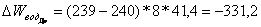 а
а 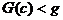 амають однаковий розмр та сну
амають однаковий розмр та сну
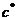 ;
;
 , якщо А В мають однаковий розмр та сну
, якщо А В мають однаковий розмр та сну
АС
(дистрибутивнсть).
Доведемо першу рвнсть за вказаних мов. Нехай А ма
розмр 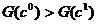 В С -
В С -  А
(В + С) дорвню
А
(В + С) дорвню
 а
а
Елементи добуткв АВ, АС дорвнюють вдповдно,
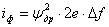 .
.
Тому елемент матриц АВ + АС дорвню

(тут була використана властивсть 2 символу суми - адитивнсть).
Отже, вдповдн елементи матриць А (В + С), АВ + АС рвн. Тому перша рвнсть доведена. Друга рвнсть доводиться аналогчно.
4. АЕ = е = А,
де А - квадратна матриця, Е - одинична матриця того ж порядку n.
Справд, елемент добутку АЕ дорвню
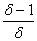
елемент добутку е дорвню

5. Якщо квадратна матриця А ма
обернену матрицю, то обернена матриця
дина.
Справд, нехай В С - обернен до А матриц. Тод
 АВ = ВА
= Е АС = СА = Е.
АВ = ВА
= Е АС = СА = Е.
Тод
С = СЕ = С (АВ) = (СА) В = ЕВ = В
(тут використан властивост 4, 2 множення матриць).
6. Якщо квадратн матриц А В мають обернен, то
 а
а 
(переврити самостйно !)
1.7. Властивост транспонування
1.
для довльно
2.

де А В - довльн матриц однакових розмрв (адитивнсть);
3.

для довльно
4.

для довльних матриць А В, для яких сну
добуток АВ;
5.

Доведемо ц властивост.
1. Очевидно.
2. Справд, 
 а=
а= 
3. Справд,
4. Нехай U = АВ. Тод

тобто  а=
а=  .
.
5. Доведемо першу з рвностей. Використа
мо попередню першу властивост:

Матриця А, для яко
Таким чином, матриця  азавжди симетрична.
азавжди симетрична.
Приклад:
 Ц симетрична матриця.
Ц симетрична матриця.
1.8. Обернена матриця у випадку квадратних матриць другого порядку
Приклад.
Розглянемо матрицю 



 аотрима
аотрима
мо дв системи:
 а
а 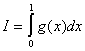
Оскльки 

 тобто
тобто 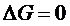 Очевидно, що така рвнсть друга рвнсть системи виконуватися одночасно не можуть. Отже ма
Очевидно, що така рвнсть друга рвнсть системи виконуватися одночасно не можуть. Отже ма
мо протирччя. Таким чином, матриця А обернено
Приклад.
Нехай матриця 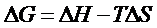 А ма
А ма
обернену матрицю знайдемо ?.
снування матриц, обернено

Припустимо, що такий розвТязок справд сну
, тод з 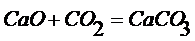 аотрима
аотрима
мо системи:
 а
а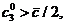
Зрозумло, що тод 
Отже, з снування розвТязку виплива
, що вн дорвню
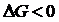
Легко переконатися, що справд
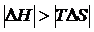
Таким чином  асну
асну
дорвню

Для кожно
Визначником матриц  аназива
аназива
ться число

Зрозумло,
що 
Лема. Якщо А В - дв квадратн матриц другого порядку, то

Доведення. Справд,
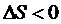
=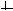 а=
а=
Ц
Ц
= а
а
Лему доведено.
Твердження. Для того, щоб квадратна матриця А другого порядку мала обернену матрицю, необхдно достатньо, щоб  а
а
Доведення. Нехай матриця А ма
обернену матрицю В. Тод АВ = ВА = Е, де 
За лемою 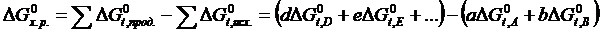


 а
а
Навпаки, нехай  Покажемо, що матриця
Покажемо, що матриця
 а
а
оберненою до А. Справд,
 а
а
 а
а
Твердження доведено.
Приклад.
Нехай  Тод
Тод 
Отже, А ма
обернену матрицю

Приклад.
Нехай 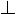 Тод
Тод 
Отже,  асну
асну
дорвню
матриц 
Квадратна матриця А другого порядку назива
ться особливою
(або виродженою), якщо  а неособливою (невиродженою),
якщо
а неособливою (невиродженою),
якщо 
1.9. Приклади матриць, елементами яких
вектори
До цього часу ми розглядали лише так матриц, елементами яких
числа. Проте в математиц використовуються також матриц, елементами яких
сам матриц. Неявно ми вже використовували
 (1)
(1)
де  а- рядок матриц А,
а- рядок матриц А, 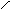 Ц стовпець матриц
Ц стовпець матриц  АВ ми визначали, як
АВ ми визначали, як
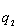 (2)
(2)
де 
Якщо б  ав (1) ми вважали б звичайними числами визначали б добуток А
В звичайним способом (за означенням добутку матриць, елементами яких
ав (1) ми вважали б звичайними числами визначали б добуток А
В звичайним способом (за означенням добутку матриць, елементами яких
числа), то ми також одержали б добуток АВ, визначений формулою (2). - мркування можна поширити на бльш загальний випадок матриць, елементами яких
матриц. Проте тут ми цього робити не будемо, лише обмежимося конкретними прикладами.
Приклад 1.
Нехай  а- двовимрн вектори,
а- двовимрн вектори,  а- числа. Тод
а- числа. Тод

Справд, 
Приклад 2.
Нехай  Ц двовимрн вектори,
Ц двовимрн вектори,  Ц матриця з числовими елементами. Тод
Ц матриця з числовими елементами. Тод  а
а
(тут на А можна дивитися як на матрицю  аз елементом А, при цьому, очевидно, добутки
аз елементом А, при цьому, очевидно, добутки  абудуть визначен).
абудуть визначен).
Справд, 
Приклад 3.
Нехай  Ц матриця з числовими елементами,
Ц матриця з числовими елементами,  а
а Ц двовимрн вектори.
Ми не можемо визначити
Ц двовимрн вектори.
Ми не можемо визначити  аподбно до того, що було в приклад 2, оскльки
аподбно до того, що було в приклад 2, оскльки  а
а


Справд, 
Доведемо тепер одне твердження, яке буде потрбне нам дал.
Твердження. Нехай А - матриця  Ц двовимрн вектори
виконуються рвност:
Ц двовимрн вектори
виконуються рвност:
 (3)
(3)
де  Ц деяк числа
Ц деяк числа  Якщо
Якщо 

де 
Доведення. Використа
мо попередн приклади. З рвностей (3) отрима
мо, що

Тод з прикладв (2) - (3) ма
мо, що
 атобто
атобто 
З твердження про необхдну достатню мову снування обернено
1.10. Числовий n - вимрний простр
Множину сх n - вимрних векторв

з дйсними [комплексними] елементами позначають через
 а називають дйсним [комплексним] n - вимрним простором.
а називають дйсним [комплексним] n - вимрним простором.
Властивост дй 1 - 9 числового n - вимрного простору (що подан нижче) випливають з вдповдних властивостей 1 - 8 додавання множення матриць на числа:
1.
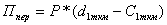
2.
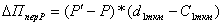
3.
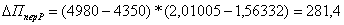
4.
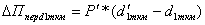
5.
6.

7.

8.

9.

(для довльних  а
а 
Лнйною комбнацúю векторв  аназива
аназива
ться вектор 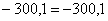
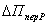 Ц числа.
Ц числа.
В числовому n - вимрному простор кожен вектор 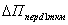 аможна представити у вигляд нйно
аможна представити у вигляд нйно

де 
Дал всюди ми використовуватимемо позначення  атльки для вказаних векторв.
атльки для вказаних векторв.
1.11. Подбн матриц
Будемо говорити, що квадратна матриця А порядку n
подбною до квадратно


В цьому випадку пишуть наступне: 
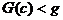
Властивост подбност:
1.
 а~
а~  а(рефлексивнсть).
а(рефлексивнсть).
Справд,
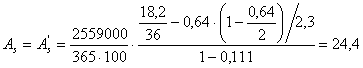 а
а
2.
Якщо  а~
а~ 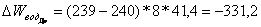
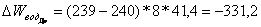 а~
а~  а(симетричнсть).
а(симетричнсть).
Справд,
якщо 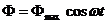


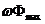
3.
Якщо  а~
а~ 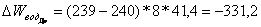 а
а 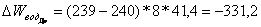 а~
а~ 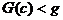

Справд,
якщо  а~
а~  а
а  а~
а~ 
 ащо
ащо 


Класом подбних матриць будемо називати вс матриц, що
подбними до дано
1.12. Вправи
1. Матрицю  аподати, як нйну комбнацю матриць:
аподати, як нйну комбнацю матриць:
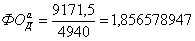
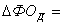






2. Нехай  Тязково
Тязково  ?
?
3. Обчислити 

4. Коли справджуються рвност  а
а 
5. Довести, що добуток двох симетричних матриць
симетричною
матрицею тод й тльки тод, коли ц матриц комутують.
6. Квадратна матриця  аназива
аназива
ться кососиметричною, якщо 
Довести, що всяку квадратну матрицю можна представити як суму
симетрично
7. Обчислити 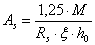
8. Довести: якщо 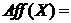
порядку.
9. Довести формулу 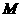
10. Довести, що добуток двох верхнх (нижнх) трикутних матриць
однакового розмру
верхньою (нижньо
Роздл 2. Системи нйних рвнянь
2.1. Система двох нйних рвнянь з двома невдомими
Нехай ма
мо систему двох нйних рвнянь з двома невдомими 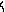
 (1)
(1)
В даному пункт розглядатимемо лише так системи.
РозвТязком тако

Система може не мати розвТязкв, може мати
диний розвТязок, або мати бльше одного розвТязку.
Приклади:
1). 
Дана система розвТязкв не ма
.
2). 
Дана система ма
диний розвТязок 
3). 
Дана система ма
безлч розвТязкв  аде
аде  Ц довльне число.
Ц довльне число.
Справд,  а
а 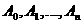 адля довльного числа
адля довльного числа 
Дв системи рвнянь називаються рвносильними (екввалентними), якщо вони мають однаков множини розвТязкв. Система рвнянь назива
ться сумсною, якщо вона ма
хоча б один розвТязок.
Система рвнянь назива
ться несумсною, якщо вона не ма
жодного розвТязку, тобто множина розвТязкв
порожня множина Ø.
Матриця  аназива
аназива
ться матрицею системи (1). Систему (1) зручно записувати в матричному вигляд
 (2)
(2)
де 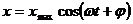
Форму (2) запису системи (1) називають матричною. Крм тако


 а (3)
а (3)
також у векторнй форм:
 (4)
(4)
де
 Ц стовпц матриц
Ц стовпц матриц 
Доведемо ряд важливих тверджень про розвТязки систем двох нйних рвнянь з двома невдомими.
Лема 1. Якщо матриця  а
а
неособливою, то система (1) ма
диний розвТязок.
Доведення.
Оскльки матриця  а
а
неособливою, то для не
Зрозумло, що вектор  Ц розвТязок системи
(1). Справд,
Ц розвТязок системи
(1). Справд, 
Покажемо, що це
диний розвТязок системи (1). Справд, нехай  а- аякийсь розвТязок системи (1). Тод
а- аякийсь розвТязок системи (1). Тод 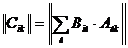
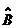


Лему доведено.
Лема 2. Якщо матриця  а
а
особливою, то система 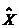 ама
ама
ненульов розвТязки.
Доведення.
1). Нехай А ннЦ нуль-матриця, тод 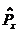
Отже,  а- ненульовий розТязок системи
а- ненульовий розТязок системи 
2). Нехай А - не
нуль-матрицею. Тому не вс  адорвнюють нулю.
адорвнюють нулю.
Зрозумло, що
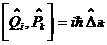
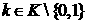

Оскльки не вс  адорвнюють нулю, то з останнх двох рвностей виплива
адорвнюють нулю, то з останнх двох рвностей виплива
, що система 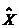 ама
ама
ненульов розвТязки.
Лему доведено.
Теорема. Система (1) ма
диний розвТязок тод тльки тод, коли матриця ц㺿 системи неособлива.
Доведення. З леми 1 виплива
, що якщо А неособлива, то система (1) ма
диний розвТязок.
Навпаки. Нехай система (1) ма
диний розвТязок  Покажемо, що тод система
Покажемо, що тод система 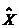 ама
ама
теж
диний розвТязок (нуль-вектор).
Справд,
припустимо, що ненульовий вектор  арозвТязок
арозвТязок 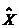 а Тод
а Тод  Ц розвТязок системи
(1). Справд,
Ц розвТязок системи
(1). Справд,  Зрозумло, що
Зрозумло, що 

Отже, система (1) ма
принаймн два рзн розвТязки. Суперечнсть.
Отже, наше припущення хибне. Тому 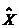 ама
ама
лише один розвТязок. За лемою 2 А - неособлива матриця.
Теорему доведено.
Наслдок. Система 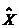

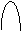 ама
ама
лише нульовий розвТязок тод тльки тод, коли 
2.2. Системи нйних рвнянь: основн означення
Нехай ма
мо систему з  алнйних рвнянь з
алнйних рвнянь з 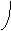 аневдомими
аневдомими 
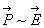 (1)
(1)
де  Ц деяк числа.
Зокрема, можливо, що
Ц деяк числа.
Зокрема, можливо, що 
РозвТязком системи (1) назива
ться будь-яка впорядкована сукупнсть чисел 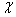 аяка задовольня
аяка задовольня
систему, що означа
наступне: якщо в кожне рвняння системи замсть 
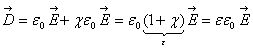 ато одержимо k
правильних числових рвностей. Отже, розвТязок системи можна вважати вектором з
n компонентами.
ато одержимо k
правильних числових рвностей. Отже, розвТязок системи можна вважати вектором з
n компонентами.
Систему називають сумсною, якщо вона ма
хоча б один розвТязок; у протилежному випадку система назива
ться несумсною (тобто коли не сну
жодно
Приклади:
1. Система
 а
а
сумсною, оскльки  Ц ? розвТязок.
Ц ? розвТязок.
Справд,
 а
а  Ц сукупнсть правильних числових рвностей.
Ц сукупнсть правильних числових рвностей.
2. Система

несумсною.
Справд,
якби вектор  абув ? розвТязком, то тод б
абув ? розвТязком, то тод б 

Введемо позначення:


Тод систему (1) можна записати у матричному вигляд:
 (2)
(2)
Матриця  аназива
аназива
ться матрицею системи (1). При
днавши до матриц А стовпець вльних членв 



 (3)
(3)
Зрозумло, що система нйних рвнянь однозначно визнача
ться сво
ю розширеною матрицею.
Дв системи називаються рвносильними (екввалентними), якщо множини
Зауважимо, що нод систему нйних рвнянь (1) зручно записувати у векторнй форм:
 (4)
(4)
де 
 Ц стовпц матриц
Ц стовпц матриц 
2.3. Елементарн перетворення системи нйних рвнянь
Сумою лнйних рвнянь 

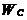
Добутком лнйного рвняння  ана число
ана число 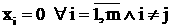 аназива
аназива
ться нйне рвняння 
Нехай ма
мо дв системи з однаковим числом невдомих. Кажуть, що друга система творена з першо

cистема 1 а~ cистема 2.
cистема 2.
Кажуть, що друга система творена з першо

система 1 ~ система 2.
Зауваження. Легко бачити, що якщо з першо
Приклад.
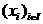 ~а а
~а а

~ 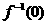
Теорема. Елементарн перетворення переводять систему нйних рвнянь в рвносильну
Перед доведенням ц㺿 теореми доведемо допомжну лему.
Лема. Якщо друга система нйних рвнянь одержу
ться з першо
Доведення. У випадку елементарного перетворення типу А твердження леми очевидне.
Нехай перша система нйних рвнянь ма
вигляд
 (1)
(1)
де 

 Ц розвТязок першо
Ц розвТязок першо
 (2)
(2)
Помножимо почастинно 
 а одержимо правильну числову рвнсть
а одержимо правильну числову рвнсть
Додамо почастинно до -то
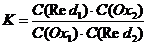
тобто
 (3)
(3)
Отже, правильними
наступ числов рвност
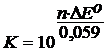 (4)
(4)
Вс рвност в (4) т сам, що в (2), лише -та рвнсть замнена рвнстю (3). Отже,  а
а
також розв¢язком то
Лему доведено.
Доведення теореми.
Нехай друга система нйних рвнянь одержу
ться з першо
Теорему доведено.
2.4. Схдчаст системи
Схдчастою назива
ться така система нйних рвнянь, матриця яко
 (1)
(1)
де 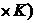 а
а а
а а
а
бо система вигляду

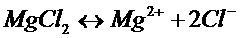

тобто система назива
ться схдчастою, якщо у розширенй ? матриц  аматриця А схдчаста.
аматриця А схдчаста.
Приклади схдчастих систем:
1). 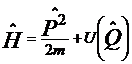 Ц схдчаст система, що склада
Ц схдчаст система, що склада
ться з одного рвняння (тут 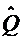 а
а ).
).
2). 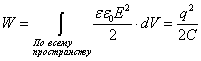 Ц схдчаста систем (тут
Ц схдчаста систем (тут 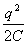 ).
).
3). 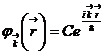 Ц схдчаста система (тут
Ц схдчаста система (тут  ).
).
Системи виду  амають множину розв¢язкв, що склада
амають множину розв¢язкв, що склада
ться з сх векторв 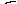 аде
аде  а- довльн числа, якщо
а- довльн числа, якщо  асистеми виду
асистеми виду  а
а
несумсними,
якщо хоч одне з чисел 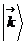 авдмнне вд 0.
авдмнне вд 0.
Тому розглянемо системи виду (1).
В такй систем невдом
 аназиваються головними невдомими, вс нш невдом - вльними невдомими.
аназиваються головними невдомими, вс нш невдом - вльними невдомими.
Розглянемо два випадки:
. Нехай серед чисел  ахоч одне вдмнне вд 0. Тод система (1) мстить рвняння
ахоч одне вдмнне вд 0. Тод система (1) мстить рвняння
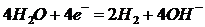
де  .
.
Зрозумло, що жодна сукупнсть чисел 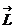 ане задовольня
ане задовольня
рвняння. Отже, система (1) розв¢язкв нема
. Тобто (1) - несумсна система.
². Нехай  Для зручност подальших мркувань зробимо перепозначення невдомих
Для зручност подальших мркувань зробимо перепозначення невдомих  абуквами
абуквами  , так щоб головн невдом
, так щоб головн невдом 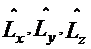 абули позначен вдповдно через
абули позначен вдповдно через  , вс нш (тобто вльн невдом) через нш
, вс нш (тобто вльн невдом) через нш 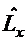 .
.
У вдповдност до цього елементи матриц А системи (1) будуть перепозначен на елементи матриц С, тобто система (1) матиме наступний вигляд:
 (2)
(2)
де 
(Рвняння системи (1),
починаючи з 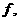 -го мали вигляд
-го мали вигляд  а тому ми
а тому ми
Надамо вльним невдомим  адовльним чином конкретн числов значення
адовльним чином конкретн числов значення  Тод з останнього рвняння однозначно визнача
Тод з останнього рвняння однозначно визнача
ться  , саме:
, саме:

 (3)
(3)
Тод з попереднього рвняння ( -го рвняння) можна однозначно визначити
-го рвняння) можна однозначно визначити  а т. д.
а т. д.
Якщо вже визначен  ато з -го рвняння
ато з -го рвняння

 авизнача
авизнача
ться однозначно

Так,
рухаючись вгору по систем, будуть однозначно визначен  атобто будуть однозначно визначен с головн невдом через числа
атобто будуть однозначно визначен с головн невдом через числа  .
.
Отже, система (2), тому система (1)
сумсними, причому при  асистема ма
асистема ма
диний розв¢язок, при  абльше, нж один розв¢язок. Зрозумло, що с розв¢язки системи (2) отримуються вказаним методом. Тобто ми можемо знайти вс розв¢язки системи.
абльше, нж один розв¢язок. Зрозумло, що с розв¢язки системи (2) отримуються вказаним методом. Тобто ми можемо знайти вс розв¢язки системи.
Приклад. Нехай ма
мо систему
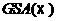
Ця система схдчаста ма
вигляд (1) ( аголовн невдом;
аголовн невдом; 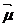 авльн невдом). Нехай
авльн невдом). Нехай  аде
аде  адовльн числа.
Тод з останнього рвняння системи ма
адовльн числа.
Тод з останнього рвняння системи ма
мо

тод можна визначити 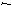 аз першого рвняння
аз першого рвняння

тобто 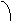 а
а
Таким чином,  Ц множина сх розв¢язкв дано
Ц множина сх розв¢язкв дано
2.5. Зведення системи лнйних рвнянь до схдчастого вигляду (метод Гаусса)
В пункт 2.4 було наведено метод розв¢язання схдчастих система (обернений хд методу Гаусса - послдовне знаходження головних невдомих 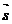 ачерез вльн невдом). В цьому пункт ми покажемо, що кожна система нйних рвнянь за допомогою скнченного числа елементарних перетворень може бути зведена до системи схдчастого вигляду (прямий хд методу Гаусса). Враховуючи те, що елементарн перетворення переводять систему в рвносильну
ачерез вльн невдом). В цьому пункт ми покажемо, що кожна система нйних рвнянь за допомогою скнченного числа елементарних перетворень може бути зведена до системи схдчастого вигляду (прямий хд методу Гаусса). Враховуючи те, що елементарн перетворення переводять систему в рвносильну
Теорема. Кожна система нйних рвнянь за допомогою скнченного числа елементарних перетворень зводиться до системи схдчастого вигляду.
Доведення теореми для випадку системи з трьох рвнянь з чотирма невдомими.
Спочатку ми доведемо цю теорему для випадку системи, що склада
ться з 3-ох рвнянь ма
4-и невдом. Справд, нехай ма
мо систему:
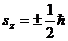 (S1)
(S1)
Будемо вважати, що матриця дано
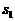 (S1¢)
(S1¢)
Причому можна вважати,
що  Цього можна завжди домогтися перестановкою рвнянь (елементарне перетворення), оскльки стовпець
Цього можна завжди домогтися перестановкою рвнянь (елементарне перетворення), оскльки стовпець  ненульовий. Для того, щоб коефцúнт при
ненульовий. Для того, щоб коефцúнт при 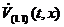 ав другому
в третьому рвняннях зробити рвним 0, додамо до другого рвняння перше,
помножене на
ав другому
в третьому рвняннях зробити рвним 0, додамо до другого рвняння перше,
помножене на  , до третього додамо перше, помножене на
, до третього додамо перше, помножене на  . Таким чином, здйснивши дан елементарн перетворення, ми одержимо систему, в якй
. Таким чином, здйснивши дан елементарн перетворення, ми одержимо систему, в якй  авходить тльки до першого рвняння:
авходить тльки до першого рвняння:
 (S2)
(S2)
Можлив випадки 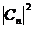 бо
бо  . Якщо
. Якщо  , то система (S2) ма
, то система (S2) ма
схдчастий вигляд. Тому вважатимемо, що 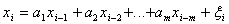
Якщо матриця

нульова, то система (S2) вже ма
схдчастий вигляд. Розглянемо випадок, коли така матриця  аненульова. Тод в матриц
аненульова. Тод в матриц 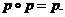 ахоча б один стовпець ненульовий. Номери стовпцв матриц
ахоча б один стовпець ненульовий. Номери стовпцв матриц  азмнюються вд
азмнюються вд  адо 4. Серед усх ненульових стовпцв матриц
адо 4. Серед усх ненульових стовпцв матриц  авиберемо стовпець з найменшим номером
авиберемо стовпець з найменшим номером  . Тод система (S2) ма
. Тод система (S2) ма
вигляд
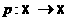 (S2¢)
(S2¢)
Причому можна вважати,
що  . Цього можна завжди домогтися перестановкою рвнянь
(елементарне перетворення), оскльки стовпець
. Цього можна завжди домогтися перестановкою рвнянь
(елементарне перетворення), оскльки стовпець 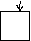 аненульовий. Для того, щоб у третьому рвнянн системи (S2¢) коефцúнт при
аненульовий. Для того, щоб у третьому рвнянн системи (S2¢) коефцúнт при 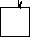 азробити рвним
0, додамо до третього рвняння друге, помножене на
азробити рвним
0, додамо до третього рвняння друге, помножене на 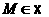 . Таким чином, здйснивши елементарне перетворення над системою (S2¢), ми одержимо систему схдчастого вигляду.
. Таким чином, здйснивши елементарне перетворення над системою (S2¢), ми одержимо систему схдчастого вигляду.
Теорему для даного випадку доведено.
Доведення теореми для загального випадку.
Доведення проводимо ндукцúю за числом рвнянь дано
1). Якщо система склада
ться лише з одного рвняння  , то вона
, то вона
схдчастою.
2). Припустимо, що система з числом рвнянь  а
а ашляхом елементарних перетворень зводиться до схдчасто
ашляхом елементарних перетворень зводиться до схдчасто
3). Покажемо, що тод
система з числом рвнянь 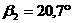 ашляхом елементарних перетворень зводиться до схдчасто
ашляхом елементарних перетворень зводиться до схдчасто
Справд, нехай ма
мо систему, що ма
 рвнянь
рвнянь
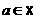 (1)
(1)
Якщо матриця дано
 (2)
(2)
Можна вважати, що  . Цього можна завжди домогтися шляхом елементарного перетворення перестановки рвнянь системи, оскльки
. Цього можна завжди домогтися шляхом елементарного перетворення перестановки рвнянь системи, оскльки  Ц ий стовпець матриц системи ненульовий.
Ц ий стовпець матриц системи ненульовий.
Зробимо над системою (2) так елементарн перетворення (типу В), щоб в сх рвняннях,
починаючи з 2-го, коефцúнти при  астали нульовими:
астали нульовими:
 до
2-го рвняння додамо перше, помножене на
до
2-го рвняння додамо перше, помножене на 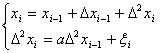
до 3-го рвняння додамо перше,
помножене н  а т. д.,
а т. д.,
до 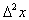 го рвняння додамо перше, помножене на
го рвняння додамо перше, помножене на 
Отрима
мо таку систему:
 (3)
(3)
Використовуючи до системи з останнх  го рвняння наше припущення, отрима
го рвняння наше припущення, отрима
мо що та система шляхом елементарних перетворень зводиться до схдчастого вигляду:
 (4)
(4)
де 
Тому вся система (3) зведеться до схдчастого вигляду:
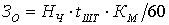 (5)
(5)
де  а
а а
а
Теорему доведено.
2.6. Вправи
1. Дослдити систему рвнянь знайти ? розвТязки в залежност вд значень
параметра 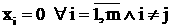
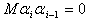
2. Переконатися, що елементарн перетворення 
одержати, помноживши ? злв на одиничну матрицю k-го порядку, над
якою виконано вдповдне перетворення.
3. Довести, що будь-яку матрицю, елементами яко
елементарними перетвореннями до схдчастого вигляду (при цьому рядки
можна множити лише на цл числа).
4. Якщо кльксть невдомиха нйно
то система не може мати
диного розвТязку. Довести.
Роздл 3. Жорданова форма матриць та матричн рвняння
3.1. Слд квадратно
Слдом квадратно
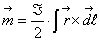
де n - порядок матриц А.
Лема. Нехай А В - дв квадратн матриц 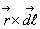 го порядку. Тод
го порядку. Тод 
Доведення. Справд, елемент  адобутку С = АВ дорвню
адобутку С = АВ дорвню
 елемент
елемент  адобутку
адобутку  адорвню
адорвню
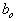 Тод
Тод  а
а За властивостями знаку суми ма
За властивостями знаку суми ма
мо право перейменувати i на 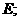 а
а 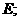 ана i
одночасно:
ана i
одночасно:

Дал за властивстю подвйних сум

Отже, 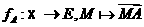
Лему доведено.
Очевидними властивостями слду
наступн:
1.
 адля довльних квадратних матриць однакового порядку.
адля довльних квадратних матриць однакового порядку.
2.
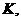 адля довльно
адля довльно
3.
 , якщо А
В подбн матриц.
, якщо А
В подбн матриц.
Справд, нехай сну
квадратна матриця X того ж порядку, як А, що  Тод за лемою
Тод за лемою 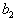
Приклад. Нехай А - квадратна матриця n-го порядку, Е - одинична матриця n-го порядку, X - невдома квадратна матриця n-го порядку. Тод рвняння  ане ма
ане ма
розв¢язкв. Справд, нехай 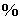 розв¢язок рвняння. Тод
розв¢язок рвняння. Тод
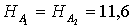 а
а 
Отже, n = 0. Суперечнсть.
3.2. Жорданова форма квадратних матриць.
Основна теорема
Тут розглядаються матриц, як, взагал кажучи, мають комплексн елементи. Жордановим блоком  арозмру
арозмру  аназива
аназива
ться  матриця
матриця
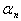
Жордановою матрицею назива
ться матриця, яка склада
ться з
жордановиха блоква
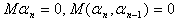 ана головнй дагонал
нулв поза цими блоками, тобто це матриця виду
ана головнй дагонал
нулв поза цими блоками, тобто це матриця виду
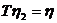 |
|
|
О |
|
О |
|
О |
|
|
О |
|
|
|
|
|
|
О |
О |
|
|
Приклад. Жорданова матриця
|
2 |
0 |
0 0 |
0 |
|
0 |
3 |
0 0 |
0 |
|
0 0 |
0 0 |
0 0 1 0 |
0 0 |
|
0 |
0 |
0 0 |
-1 |


утворена жордановими блоками:
 .
.
Основна теорема. Кожна квадратна матриця А
подбною до деяко
Доведення ц㺿 теореми ми пода
мо лише для квадратних матриць другого порядку.
3.3. Зведення до жорданово
трикутних матриць другого порядку
Будемо використовувати результати пункту 1.9. Нехай ма
мо матрицю виду
 .
.
Зведемо ? до жорданово
Тод 
Розглянемо наступн випадки:
1.
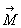
Вдповдно до твердження п. 1.9 нам потрбно знайти так  а
а 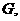 , для яких
, для яких 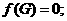 а матриця
а матриця  ама
ама
жорданову форму. Для цього необхдно зробити  бо
бо  . Покажемо, що
. Покажемо, що  аможна зробити рвним 0. Оскльки верхнй рядок матриц А в такому раз змнювати не потрбно, то покладемо
аможна зробити рвним 0. Оскльки верхнй рядок матриц А в такому раз змнювати не потрбно, то покладемо  Нам потрбно знайти такий вектор
Нам потрбно знайти такий вектор 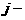 ащоб
ащоб  а
а 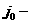
Оскльки  ато
ато  ане повинно дорвнювати 0. Дал,
ане повинно дорвнювати 0. Дал, 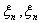
Дал, 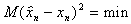 а
а
Тод 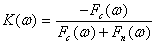
Оскльки  то з останнього рвняння системи ма
то з останнього рвняння системи ма
мо, що 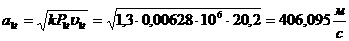 Тод з першого рвняння виплива
Тод з першого рвняння виплива
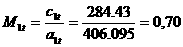
Отже, 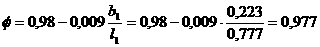 Оскльки
Оскльки 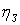 ато можемо покласти
ато можемо покласти 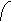 атод
атод  Тому
Тому  Отже, на пдстав твердження п. 1.9
Отже, на пдстав твердження п. 1.9 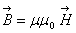 аде С визнача
аде С визнача
ться з рвностей
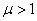
тобто 
 .
.
2.
Нехай  .
.
Випадки:
2.1.
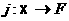 .
.
Тод матриця А вже ма
жорданову форму.
2.2.
 . Тода
. Тода
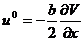
Помножимо останн
рвняння на число а
а
Тод 
Якщо ввести перепозначення:
 ато
ато 
 На пдстав твердження п 1.9 матимемо, що
На пдстав твердження п 1.9 матимемо, що  аде
аде 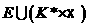
3.4. Власн значення та власн вектори квадратно
Число  а(комплексне)
назива
а(комплексне)
назива
ться власним числом квадратно
 .
(1)
.
(1)
Ненульовий вектор 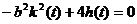 аназива
аназива
ться власним вектором матриц А, якщо

для деякого власного значення 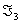 аматриц А.а
аматриц А.а
Рвнсть (1)
екввалентна рвност 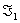 аде
аде  аяка екввалентна такй рвност
аяка екввалентна такй рвност
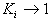
де  .
.
Теорема.
Для того, щоб число 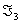 абуло власним значенням, необхдно достатньо виконання рвност
абуло власним значенням, необхдно достатньо виконання рвност 
Необхднсть. Нехай
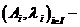 а- власне значення, тод
а- власне значення, тод  адля деякого власного вектора
адля деякого власного вектора 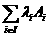 , тобто
, тобто 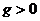 Оскльки
Оскльки 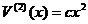 ато це означа
ато це означа
, що система
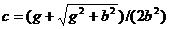
ма
ненульовий розв¢язок. Тому 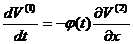 Оскльки визначник при транспонуванн не змню
Оскльки визначник при транспонуванн не змню
ться, то  а
а
Достатнсть. Доведення достатност проводиться в зворотному порядку.
Проведть його самостйно! (Див. наслдок п. 2.1).
Теорему доведено.
Рвняння
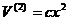 авдносно невдомого
авдносно невдомого  аназива
аназива
ться характеристичним рвнянням матриц А. З нього знаходимо власн значення. Зрозумло, що

Отже, характеристичне рвняння можна записати так
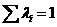
Для знаходження власних векторв матриц А потрбно розв¢язати систему

тобто 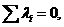
для кожного власного значення 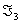 , вибрати ненульов розв¢язки, як снують в силу
, вибрати ненульов розв¢язки, як снують в силу 
Зауваження 1. Оскльки кожне квадратне рвняння ма
два комплексн розв¢язки, якщо врахувати
Зауваження 2. Характеристичн рвняння подбних матриць однаков. Справд, нехай 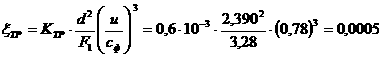 Тод
Тод
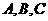 Приклад. Нехай
Приклад. Нехай 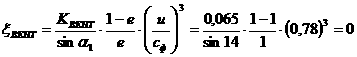 Тод
Тод  Ц характеристичне рвняння. Зрозумло, що
Ц характеристичне рвняння. Зрозумло, що 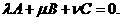 Ц множина сх власних значень матриц А.
Ц множина сх власних значень матриц А.
3.5. Зведення квадратно
Нехай 
Згдно з попереднм завжди сну
ненульовий вектор  а(власний вектор для А), для якого
а(власний вектор для А), для якого  апри деякому
апри деякому  а(власне значення).
а(власне значення).
Нам потрбно звести А до нижньо
 а
а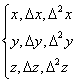
Тому за 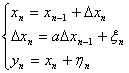 аможна взяти власний вектор
аможна взяти власний вектор 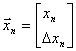 аматриц А. Тод зрозумло, що
аматриц А. Тод зрозумло, що  Ц вдповдне власне значення. Тод для визначення
Ц вдповдне власне значення. Тод для визначення 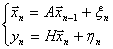 адосить так пдбрати
адосить так пдбрати  а
а 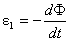 , щоб
, щоб 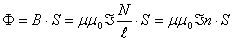 а(другий рядок матриц С може бути довльним - це не порушу
а(другий рядок матриц С може бути довльним - це не порушу
нижньо
1.
 , тод для того, щоб
, тод для того, щоб  аможна взяти
аможна взяти 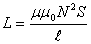 атобто
атобто 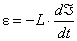 Тод
Тод 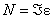 аде
аде 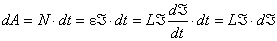 .
.
2.
 атод для того, щоб
атод для того, щоб 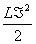 аможна взяти
аможна взяти  атобто
атобто 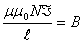 Тод
Тод 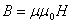 аде
аде 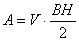
3.6. Загальний випадок
Довльна квадратна матриця  а
а
подбною до деяко
Приклад. Нехай ма
мо матрицю 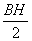 Тод
Тод 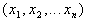 Тому
Тому  Ц характеристичне рвняння. Воно ма
Ц характеристичне рвняння. Воно ма
два однаков корен 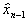 Знайдемо власн вектори з системи
Знайдемо власн вектори з системи
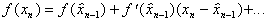
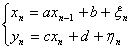 а- один з ненульових розв¢язкв (тут
а- один з ненульових розв¢язкв (тут 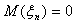 ).
).
Оскльки  ато згдно з попереднм
ато згдно з попереднм  аздйсню
аздйсню
перехд до трикутно
Оскльки 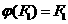 а
а  ато вдповдно до попереднього за Y можна взяти матрицю
ато вдповдно до попереднього за Y можна взяти матрицю  Тод знову вдповдно до попереднього
Тод знову вдповдно до попереднього  а
а  Тому
Тому  аде
аде  .
.
Отже, 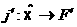
3.7. Однозначнсть визначення жорданово
з точнстю до порядку слдування дагональних блокв
Лема.
(). Для довльних чисел a1, а2, с1, с2
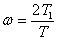 бо
бо  .
.
(ó). Для довльних чисел а1, а2, u

(㳳). Для довльних чисел u v
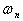
Доведення.
) 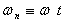 Нехай
Нехай

Тод характеристичн рвняння цих матриць однаков (бо матриц подбн)
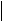 .
.
Отже, множини

тобто 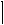 бо
бо 
У випадку, коли множина коренв одноелементна останн
твердження очевидне.
 Якщо
Якщо  ато очевидно, що
ато очевидно, що

Якщо жа 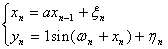 ато
ато
 аоскльки
аоскльки  а(переврити!).
а(переврити!).
ó). Припустимо, що для деяких а1, а2, u

Тод характеристичн рвняння цих матриць

спвпадають, отже, спвпадають множини
Оскльки  ато сну
ато сну
така неособлива матриця Т, що
 ле
ле  .
.
ле тод  Суперечнсть.
Суперечнсть.
㳳).  Очевидно.
Очевидно.
 Якщо
Якщо  ато характеристичн рвняння цих матриць
ато характеристичн рвняння цих матриць

однаков, отже спвпадають множини
Лему доведено.
Зауваження. Жорданова матриця  аможе складатися або з двох жорданових блокв
аможе складатися або з двох жорданових блокв  , або з одного жорданового блока
, або з одного жорданового блока  .
.
Ми вже показали, що квадратна матриця А другого порядку
подбною до деяко
Доведемо тепер, що справедливе наступне твердження.
Твердження. Жорданова матриця J, що
подбною до матриц А, визнача
ться однозначно з точнстю до порядку слдування дагональних жорданових блокв.
Доведення.
Нехай матриця А подбна до жорданово
Твердження доведено.
3.8. Спектр квадратно
Множина сх власних значень квадратно
Теорема. Квадратна матриця А другого порядку з простим спектром подбна до дагонально
Доведення. Оскльки така матриця А
подбною до жорданово
Суперечнсть.
Теорему доведено.
3.9. Рвняння 
.
Розглянемо спочатку рвняння  , в якому
, в якому  Х - невдома квадратна матриця другого порядку. Нехай Х0 - якийсь розвТязок цього рвняння. Тод сну
Х - невдома квадратна матриця другого порядку. Нехай Х0 - якийсь розвТязок цього рвняння. Тод сну
(згдно попереднх пунктв) матриця Т, для яко
1).  бо 2).
бо 2).  аде а1, а2, - числа
(комплексн).
аде а1, а2, - числа
(комплексн).
1). Нехай  Тод
Тод  Тому
Тому 
Отже,  Тод
Тод  .
.
Отже,  .
.
Переврка показу
, що О справд
розвТязком рвняння.
2). Нехай  Тод
Тод  Тому
Тому 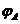 . Отже,
. Отже,  . Тод
. Тод  . Отже,
. Отже, 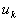
Нехай Т - довльна неособлива матриця, тод 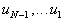 а- розвТязок рвняння.
а- розвТязок рвняння.
Справд, 
Таким чином, множина всх розвТязкв рвняння 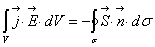 асклада
асклада
ться з усх матриць 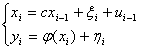 аде Т - довльна неособлива матриця, з
аде Т - довльна неособлива матриця, з 
Зауваження. Якщо задано деяке матричне рвняння  аяке ма
аяке ма
наступну властивсть: якщо Х0
- розвТязок, Т - довльна неособлива матриця, то  Ц теж розвТязок, то для його розвТязання, зрозумло, достатньо знайти розвТязок S в кожному з сх рзних класв подбних матриць (якщо такий розвТязок сну
Ц теж розвТязок, то для його розвТязання, зрозумло, достатньо знайти розвТязок S в кожному з сх рзних класв подбних матриць (якщо такий розвТязок сну
). Вс матриц в клас подбних будуть розвТязками рвняння, якщо хоч один розвТязок з цього класу сну
. Представники ж класв подбних матриць краще брати у жордановй форм, оскльки над такими матрицями легше виконувати обчислення, крм того, так матриц
диними в кожному клас подбних матриць з точнстю до порядку слдування жорданових блокв. Прикладами рвнянь з такою властивстю
 а
а 
².
РозвТяжемо тепер рвняння 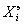 аде
аде  Х - квадратна матриця другого порядку,
використавши це зауваження.
Х - квадратна матриця другого порядку,
використавши це зауваження.
Нехай  атод
атод  атобто або
атобто або  бо
бо  бо
бо  бо
бо  Дал використову
Дал використову
мо п. 3.7. Зрозумло тод, що

Отже, 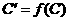 а- представники рзних класв подбних матриць, як
а- представники рзних класв подбних матриць, як
розвТязками рвняння.
Дал,
нехай 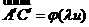 атод
атод  Отже,
Отже,  а
а 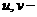 ащо неможливо.
ащо неможливо.
Отже,
вс розвТязки рвняння  атак:
атак:

де Т - довльна неособлива матриця.
 3.10. Вправи
3.10. Вправи
1. Знайти спектр матриц 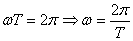 ата звести ? до дагонально
ата звести ? до дагонально
2. РозвТязати матричне рвняння 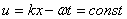 ав квадратних матрицях другого
ав квадратних матрицях другого
порядку.
3. Звести до жорданово
4. РозвТязати матричне рвняння  ав квадратних матрицях другого
ав квадратних матрицях другого
порядку, де  , використавши попередню задачу.
, використавши попередню задачу.
5. РозвТязати матричне рвняння 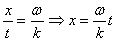 ав квадратних матрицях другого
ав квадратних матрицях другого
порядку.
6. РозвТязати матричне рвняння  ав квадратних матрицях другого
ав квадратних матрицях другого
порядку
Список тератури
1. Скорняков Л.А. Элементы алгебры. - Москва. - Наука. - 1980. - 240 с.
2. Мальцев А.И. Основы линейной алгебры. - Москва.Ц Наука. - 1970. - 400 с.
3. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. Ц
Москва. - МГУ. - 1980. - 320 с.
4. Ланкастер П. Теория матриц. - Москва. - Наука. - 1978. - 280 с.
5. Горбачук О.Л., Воробець Б.Д. Вступ до вищо