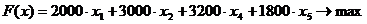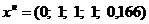Читайте данную работу прямо на сайте или скачайте

Лабораторная работ №7 по "Основам теории систем" (Решение задачи коммивояжера методом ветвей и границ)

Телешовой Елизаветы, гр. 726,

Решение задачи коммивояжера методом ветвей и границ.

1. Постановка задачи.

Испекла бабка колобок и поставила его остывать на окошко. И решил колобок, что пока он остывает, он вполне может обежать лес, посмотреть на лесных жителей и снова вернуться к деду и бабке. Сказано - сделано. Спрыгнул колобок из окошка и покатился в лес. Помогите колобку найти кратчайший маршрут его движения по лесу, если расстояния между норами лесных жителей, также домом деда и бабки даны в таблице.

	Дед и бабка	Заяц	Волк	Медведь	Лиса
Дед и бабка	0	6	4	5	2
Заяц	6	0	3	3,5	4,5
Волк	4	3	0	5,5	5
Медведь	5	3,5	5,5	0	2
Лиса	2	4,5	5	2	0

2. Математическая модель задачи.

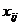
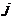Для решения задачи присвоим каждому пункту маршрута определенный номер: дед и бабка - 1, заяц - 2, волк Ц 3, медведь - 4 и лиса - 5. Соответственно общее количество пунктов альтернативных переменных i-того пункта в j-тый не входит в маршрут и 1 в противном случае. словия прибытия в каждый пункт и выхода из каждого пункта только по одному разу выражаются равенствами (1) и (2).

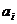(1)

(2)

Для обеспечения непрерывности маршрута вводятся дополнительно n переменных аи адополнительных ограничений (3).

(3)

Суммарная протяженность маршрута F, которую необходимо минимизировать, запишется в следующем виде:

(4)

В нашем случае эти словия запишутся в следующем виде:

а (1); а (2);

(3)

а(4)

3. Решение задачи методом ветвей и границ.

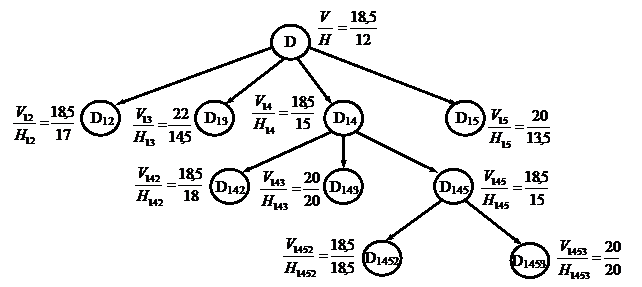
1) Анализ множества D.

Найдем оценку снизу Н. Для этого определяем матрицу минимальных расстояний по строкам (1 где расстояние минимально в строке).

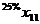а=>

налогично определяем матрицу минимальных расстояний по столбцам.

а=>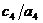

;

Выберем начальный план:

Очевидно, что 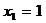аозначает переход из первого пункта в j-тый. Рассмотрим эти подмножества по порядку.

2) Анализ подмножества D₁₂.

;

3) Анализ подмножества D₁₃.

;

4) Анализ подмножества D₁₄.

;

5) Анализ подмножества D₁₅.

;

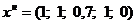
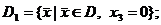
6) Отсев неперспективных подмножеств.

Подмножества D₁₃ и D₁₅ неперспективные. Т.к. 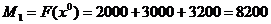D₁₄.

.

7) Анализ подмножества D₁₄₂.

;

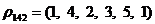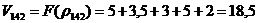
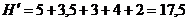
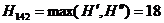
8) Анализ подмножества D₁₄₃.

;

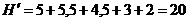
9) Анализ подмножества D₁₄₅.

;

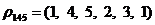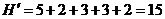
10) Отсев неперспективных подмножеств.

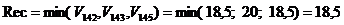
Подмножество D₁₄₃ неперспективное. Т.к. D₁₄₅.

.

9) Анализ подмножества D₁₄₅₂.

;

9) Анализ подмножества D₁₄₅₃.

;

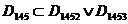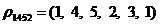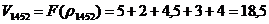
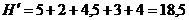
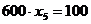
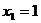
Оптимальное решение:

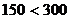
Таким образом, маршрут колобка: дед и бабка - медведь - лиса - заяц - волк - дед и бабка.

D

D12

D13

D14

D15

D142

D143

D145

D1452

D1453