Читайте данную работу прямо на сайте или скачайте

Комплексные числа

1. Введение.

1.1. ИСТОРИЧЕСКАЯ СПРАВКА

Комплексные числа были введены в математику для того, чтобы сделать возможной операцию извлечения квадратного корня из любого действительного числа. Это, однако, не является достаточным основанием для того, чтобы вводить в математику новые числа. Оказалось, что если производить вычисления по обычным правилам над выражениями, в которых встречаются квадратный корень из отрицательного числа, то можно прийти к результату, же не содержащему квадратный корень из отрицательного числа. В XVI в. Кардано нашел формулу для решения кубического равнения. Оказалось, когда кубическое равнение имеет три действительных корня, в формуле Кардано встречается квадратный корень из отрицательного числа. Поэтому квадратные корни из отрицательных чисел стали употреблять в математике и назвали их мнимыми числами - тем самым они как бы приобрели право на нелегальное существование. Полные гражданские права мнимым числам дал Гаусс, который назвал их комплексными числами, дал геометрическую интерпретацию и доказал основную теорему алгебры, тверждающую, что каждый многочлен имеет хотя бы один действительный корень.

2. Комплексные числа в алгебраической форме.

2.1. ПОНЯТИЕ КОМПЛЕКСНОГО ЧИСЛА

Решение многих задач математики, физики сводится к решению алгебраических равнений. Поэтому исследование алгебраических равнений является одним из важнейших вопросов в математике. Стремление сделать равнения разрешимыми - одна из главных причин расширения понятия числа.

Так для решимости равнений вида X+A=B X+A=B # "# ##0" положительных чисел недостаточно. Например, равнение X+5=2а не имеет положительных корней. Поэтому приходится вводить отрицательные числа и нуль.

На множестве рациональных чисел разрешимы алгебраические равнения первой степени, т.е. равнения вид AX+B=0 (Aа Однако алгебраические равнения степени выше первой могут не иметь рациональных корней. Например, такими являются равнения X²=2, X³=5. Необходимость решения таких равнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.

Однако и действительных чисел недостаточно для того, чтобы решить любое алгебраическое равнение. Например, квадратное равнение с действительными коэффициентами и отрицательным дискриминантом не имеет действительных корней. Простейшее из них - равнение X²+1=0. Поэтому приходится расширять множество действительных чисел, добавляя к нему новые числа. Эти новые числа вместе с действительными числами образуют множество, которое называют множеством комплексных чисел.

Выясним предварительно, какой вид должны иметь комплексные числа. Будем считать, что на множестве комплексных чисел равнение X²+1=0 имеет корень. Обозначим этот корень буквой i Таким образом, i - это комплексное число, такое, что i ²= Ц1.

Как и для действительных чисел, нужно ввести операции сложения и множения комплексных чисел так, чтобы сумма и произведение их были бы комплексными числами. Тогда, в частности, для любых действительных чисел A и B выражение A+Bi можно считать записью комплексного числа в общем виде. Название лкомплексное происходит от слова составное: по виду выражения A+Bi.

Комплексными числами аназывают выражения вида A+Bi, где A и B Цдействительные числа, i - некоторый символ, такой что i²= Ц1, и обозначают буквой Z.

Число A называется действительной частью комплексного числа A+Bi, число B - его мнимой частью. Число i называется мнимой единицей.

Например, действительная часть комплексного числа 2+3iа равна 2, мнимая равна 3.

Для строгого определения комплексного числа нужно ввести для этих чисел понятие равенства.

Два комплексных числа A+Bi и C+Di называются равными тогда и только тогда, когда A=C и B=D, т.е. когда равны их действительные и мнимые части.

Пусть дано комплексное число Z=A+Bi. Сопряженным с Z называется комплексное число A - Bi, которое обозначается

A - Bi.

2.2. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ

КОМПЛЕКСНОГО ЧИСЛА

Рисунок SEQ Рисунок * ARABIC 1

Действительные числа геометрически изображаются точками числовой прямой. Комплексное число A+Bi можно рассматривать как пару действительных чисел(A;B). Поэтому естественно комплексное число изображать точками плоскости. В прямоугольной системе координат комплексное число Z=A+Biа изображается точкой плоскости с координатами (A;B), и эта точка обозначается той же буквой Z (рисунок 1). Очевидно, что получаемое при этом соответствие является взаимно однозначным. Оно дает возможность интерпретировать комплексные числа как точки плоскости на которой выбрана система координат. Такая координатная плоскость называется комплекснойа плоскостью. Ось абсцисс называется действительной осью, т.к. на ней расположены точки соответствующие действительным числам. Ось ординат называется мнимой осью - на ней лежат точки, соответствующие мнимым комплексным числам.

Рисунок SEQ Рисунок * ARABIC 2

Не менее важной и добной является интерпретация комплексного числа A+Bi акак вектора, т.е. вектора с началом в точке

O(0;0) и с концом в точке М(A;B) (рисунок 2).

Соответствие становленное между множеством комплексных чисел, с одной стороны, и множествами точек или векторов плоскости, с другой, позволяет комплексные числа точками или векторами.

2.3.МОДУЛЬ КОМПЛЕКСНОГО ЧИСЛА

Пусть дано комплексное число Z=A+Bi. Сопряженным с Z называется комплексное число A - Bi, которое обозначается

A - Bi.

Отметим, что A+Bi, поэтому для любого комплексного числа Z имеет место равенство =Z.

Модулем комплексного числа Z=A+Bi называется число аи обозначается

(1)

Это расстояние между точками либо длина. Множество комплексных чисел нельзя линейно упорядочить (сравнить).

Из формулы (1) следует, что адля любого комплексного числа Z, причема а Z=0, т.е. когда A=0 и B=0.

2.4. СЛОЖЕНИЕ И МНОЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ

Суммой двух комплексных чисел A+Biа и C+Di называется комплексное число (A+C) + (B+D)i, т.е. а(A+Bi) + (C+Di)=(A+C) + (B+D)i

Произведением двух комплексных чисел A+Biа и C+Diа называется комплексное число (AC - BD)+(AD+BC) i, т.е.

(A + Bi)(C + Di)=(AC - BD) + (AD + BC)i

Из формул вытекает, что сложение и умножение можно выполнять по правилам действий с многочленами, считая i²= Ц1. Операции сложения и множения комплексных чисел обладают свойствами действительных чисел. Основные свойства:

Переместительное свойство:

Z₁ +Z₂=Z₂+Z₁, Z₁Z₂=Z₂Z₁

(A+Bi) + (C+Di) = (A+C) + (B+D)i (C+Di) + (A+Bi) = (C+A) + (D+ B)i

(A + Bi)(C + Di) = (AC Ц BD) + (AD + BC)i (C + Di) (A + Bi) = (CA Ц DB) + (DA + CB)i

Сочетательное свойство:

(Z₁+Z₂)+Z₃=Z₁+(Z₂+Z₃), (Z₁Z₂)Z₃=Z₁(Z₂Z₃)

((A+Bi) + (C+Di)) + (E+Fi) = ((A+C) + (B+D)i )+ (E+Fi) = (A+C+E) + (B+D+F) i =Е = (A+Bi) + ((C+E) + (D+F) i) (A+Bi) + ((C+Di) + (E+Fi)) = а(A+Bi) + ((C+E) + (D+F) i) =Е= ((A+C) + (B+D)i )+ (E+Fi) = ((A+Bi) + (C+Di)) + (E+Fi)

((A + Bi)(C + Di)) (E+Fi) = ((AC Ц BD) + (AD + BC)i) (E+Fi) = Е= (A + Bi)(( C + Di)(E+Fi)) (A + Bi)(( C + Di)(E+Fi)) =Е=а (A + Bi)(( CE Ц DF) + (CF + DE)i) = ((A + Bi)(C + Di)) (E+Fi)

Распределительное свойство:

Z₁(Z₂+Z₃)=Z₁Z₂+Z₁Z_3а

(A + Bi)((C+Di)) + (E+Fi)) = ((AC Ц BD) + (AD + BC)i)+ ((AE Ц BF) + (BE + BF)i)=Е= (A + Bi)(C+Di) + (A + Bi) (E+Fi) (A + Bi)(C+Di) + (A + Bi) (E+Fi)=Е= ((AC Ц BD) + (AD + BC)i)+ ((AE Ц BF) + (BE + BF)i) = (A + Bi)((C+Di)) + (E+Fi))

2.5. Геометрическое изображение суммы комплексных чисел

Рисунок SEQ Рисунок * ARABIC 3

Согласно определению сложения двух комплексных чисел, действительная часть суммы равна сумме действительных частей слагаемых, мнимая часть суммы равна сумме мнимых частей слагаемых. Точно также определяются координаты суммы векторов:

Сумма двух векторов с координатами (A₁;B₁) и (A₂;B₂) есть вектор с координатами (A₁+A₂;B₁+B₂). Поэтому, чтобы найти вектор, соответствующий сумме комплексных чисел Z₁ и Z₂ нужно сложить векторы, соответствующие комплексным числама Z₁ и Z₂.

2.6. ВЫЧИТАНИЕ И ДЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ

Вычитание комплексных чисел - это операция, обратная сложению: для любых комплексных чисел Z₁ и Z₂ существует, и притом только одно, число Z, такое, что:

Z + Z₂=Z₁

Если к обеим частям равенства прибавить (ЦZ₂), апротивоположное числу Z₂:

Z+Z₂+(ЦZ₂)=Z₁+(ЦZ₂), откуда

Z = Z₁ Ц Z₂

Число Z=Z₁+Z₂ называют аразностью чисел Z₁ и Z₂, т.е.

Z=(A+Bi) - (C+Di)=(A-C) + (B-D)i

Деление вводится как операция, обратная множению:

Z×Z₂=Z₁

Разделив обе части на Z₂ получим:

Z=

Из этого равнения видно, что Z₂

Z= E+ Fi = (i)/ (C+Di)= (i)(C-Di)/ (C+Di)(C-Di) = ((AC + BD) + (AD - BC)i)/(C² + D²) = (AC + BD)/(C² + D²) + (AD - BC)i/(C² + D²) = E+ Fi

2.7. Геометрическое изображение разности комплексных чисела

Рисунок SEQ Рисунок * ARABIC 4

Разности Z_2а Ц Z₁ комплексных чисел Z₁ и Z₂, соответствует разность векторов, соответствующих числам Z₁ и Z₂. Модуль аразности двух комплексных чисел Z₂ и Z₁ по определению модуля есть длина вектора Z_2а Ц Z₁. Построим этот вектор, как сумму векторов Z₂ и (ЦZ₁) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.

Это важное геометрическое истолкование модуля разности двух комплексных чисел позволяет с спехом использовать простые геометрические факты.

2. 8. Возведение в степень и корень из комплексного числа.

Комплексное число также можно возводить в степень, как и другие числа, выглядит это следующим образом:

ⁿ = ZZZZZZЕ - n-раз

Квадратным корнем из комплексного числа называется выражение вида

W² = Z

а= X+Yi, A,B,X,Y

Возведем в квадрат и приравняем обе части, откуда и находятся X и Y.

2.9. Свойства комплексного числа.

         Операций сопряжения:

1.     

2.     

3.     

4.     

5.     

         Свойства модуля:

1.      Если Z, то асовпадает с понятием действительного числа

2.     

3.     

4.     

5.     

3.ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА

КОМПЛЕКСНОГО ЧИСЛА

Запись комплексного числа Z в виде A+Biа называется алгебраической формой комплексного числа. Помимо алгебраической формы используются и другие формы записи комплексных чисел.

Рисунок SEQ Рисунок * ARABIC 1

Рассмотрим тригонометрическую форму записи комплексного числа. Действительная и мнимая части комплексного числа Z=A+Bi выражаются через его модуль = r и аргумент j=argZ следующим образом:а

A= rcosj ; B= rsinj.

Число Z можно записать так:

Z= rcosj+ isinj = r(cosj + isinj)

Z = r(cosj + isinj) (2)

Эта запись называется тригонометрической формой комплексного числа.

r =Ц модуль комплексного числа.

Число j называют аргументом комплексного числа.

ргументом комплексного числа ZZ, причем величина гла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной, если производится по часовой стрелке.

Для числа Z=0 аргумент не определяется, и только в этом случае число задается только своим модулем.

Как же говорилось выше = r =

A+Bi=cosj + isinj, откуда приравнивая действительные и мнимые части, получим:

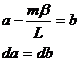cosj = sinj = (3)

Если sinj поделить на cosj получим: tgj= (4)

Эту формулу добней использовать для нахождения аргумента j, чем формулы (3). Однако не все значения j, довлетворяющие равенству (4), являются аргументами числа A+Bi. Поэтому при нахождении аргумента нужно честь, в какой четверти расположена точка A+Bi.

Декартову плоскость, которая служит для изображения комплексных чисел называется комплексной плоскостью.

Если комплексное число изобразить в полярной системе координат, то это будет выглядеть следующим образом:

j при этом называется полярным глом, r - полярным радиусом, причем

Совокупность точки О и оси ОР и единичного отрезка ОЕ называется полярной системой координат.

3.1.СВОЙСТВА МОДУЛЯ И АРГУМЕНТА

КОМПЛЕКСНОГО ЧИСЛА

Комплексные числа равны Z₁ = Z₂ а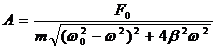r₁₌r₂ и

С помощью тригонометрической формы удобно находить произведение и частное комплексных чисел.

Пусть Z₁= r₁(cosj₁ + isinj₁), Z₂ = r₂(cosj₂ + isinj₂). Тогда:

Z₁Z₂= r₁r₂[cosj₁cosj₂ Ц sinj₁sinj₂ + i( sinj₁cosj₂ + cosj₁sinj₂)]=

= r₁r₂[cos(j₁ + j₂) + isin(j₁ + j₂)].

Таким образом, произведение комплексных чисел, записанных в тригонометрической форме, можно находить по формуле:

Z₁Z₂= r₁r₂[cos(j₁ + j₂) + isin(j₁ + j₂)] (5)

Из формулы (5) следует, что при умножении комплексных чисел их модули перемножаются, аргументы складываются.

Вывод: arg(Z₁Z₂) = arg Z₁+arg Z₂

Если Z₁=Z₂ то получим:

Z²=[r(cosj + isinj)]²= r²(cos2j + isin2j)

Z³=Z²Z= r²(cos2j + isin2j)r(cosj + isinj)=

= r³(cos3j + isin3j)

Вообще для любого комплексного числа Z= r( cosj + isinj) и любого натурального числа n справедлива формула:

Zⁿ =[ r(cosj + isinj)]ⁿ= rⁿ( cosnj+ isinnj), (6)

которую называют формулой Муавра.

Частное двух комплексных чисел, записанных в тригонометрической форме, можно находить по формуле:

cos(j₁ - j₂) + isin(j₁ - j₂)]. (7)

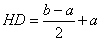
cos(Цj₂) + isin(Цj₂)

Используя формулу 5

cosj₁ + isinj₁)×( cos(Цj₂) + isin(Цj₂)) =

cos(j₁ Ц j₂) + isin(j₁ - j₂).

Вывод: arg(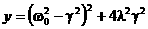arg Z₁-arg Z₂

3.2. Показательная запись комплексного числа.

Выражение вида:а аназывается формулой Эйлера, где r-модуль, 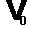а- аргумент.

Z=A+Bcos 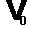а+ isin)=

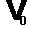При r =1, получим cos 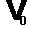а+ isin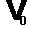а- тождество Эйлера.

Ну сопряж. ему а= cos 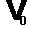а- isin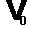

Если их сложить или вычисть, то получим следующее:

cos 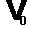а, sin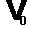

При

4.ВОЗВЕДЕНИЕ В СТЕПЕНЬ И ИЗВЛЕЧЕНИЕ КОРНЯ.

Многочлены деления круга.

Из формулы 6 видно, что возведение комплексного числ r( cosj + isinj) в целую положительную степень с натуральным показателема его модуль возводится в степень с тем же показателем, аргумент множается на показатель степени.

[ r(cosj + isinj)]ⁿ= rⁿ( cos nj + isin nj)

Число Z называется корнем степени n из числа w ( обозначается Zⁿ =w.

Из данного определения вытекает, что каждое решение равнения Zⁿ = w является корнем степени n из числа w. Другими словами, для того, чтобы извлечь корень степени n из числа w, достаточно решить равнение Zⁿ = w. Если w=0, то при любом n равнение Zⁿ = w имеет только одно решение Z= 0. Если wZ0, а, следовательно, и Z и w можно представить в тригонометрической форме

Z = r(cosj + isinj), w = p(cosy + isiny)

Уравнение Zⁿ = w примет вид:

rⁿ( cos nj + isin nj) = p( cosy + isiny)

Два комплексных числа равны тогда и только тогда, когда равны их модули, аргументы отличаются слагаемыми, кратными 2p. Следовательно, rⁿ = p и nj = y + 2pk, где kÎZ или аr = 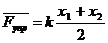аи j = kÎZ.

Итак, все решения могут быть записаны следующим образом:

Z_K=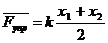[cos() + isin()], kÎZ (8)

Формулу 8 называют второй формулой Муавра.

Таким образом, если wn корней степени n из числа w: все они содержатся в формуле 8. Все корни степени n из числа w имеют один и тот же модуль 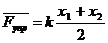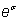n из комплексного числа w, соответствует точкам комплексной плоскости, расположенным в вершинах правильногоа n - гольника, вписанного в окружность радиуса 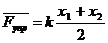ас центром в точке Z = 0.

Символ ане имеет однозначного смысла. Поэтому, потребляя его, следует четко представлять себе, что под этим символом подразумевается. Например, используя запись 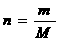i и Цi, или одно, то какое именно.

4.1. равнения высших степеней

Формула 8 определяет все корни двучленного равнения степени n. Неизмеримо сложнее обстоит дело в случае общего алгебраического равнения степени n:

a_n×Z^nа + a_nЦ1×Z^nЦ1 +...+ a₁×Z¹ + a₀ = 0 (9)

Где a_n,..., a₀ Ц заданные комплексные числа.

В курсе высшей математики доказывается теорема Гаусса:а каждое алгебраическое уравнение имеет в множестве комплексных чисел по крайней мере один корень. Эта теорема была доказана немецким математиком Карлом Гауссом в 1779 году.

Опираясь на теорему Гаусса, можно доказать, что левая часть равнения 9 всегда может быть представлен в виде произведения:

,

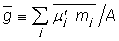Где Z₁, Z₂,..., Z_Kа Ц некоторые различные комплексные числа,

a₁,a₂,...,a_k Ц натуральные числа, причем:

a₁ + a₂ +... + a_k = n

Отсюда следует, что числ Z₁, Z₂,..., Z_K являются корнями равнения 9. При этом говорят, что Z₁ является корнем кратности a_1, Z₂ Ц корнем кратности a₂ и так далее.

Если словиться считать корень уравнения столько раз, какова его кратность, то можно сформулировать теорему: каждое алгебраическое равнение степени n имеет в множестве комплексных чисел ровно n корней.

Теорема Гаусса и только что сформулированная теорема дают решения о существовании корней, но ничего не говорят о том, как найти эти корни. Если корни первой и второй степени могут быть легко найдены, то для равнений третей и четвертой степеней формулы громоздки, для равнений степени выше четвертой таких формул вообще не существует. Отсутствие общего метода не мешает отыскивать все корни равнения. Для решения равнения с целыми коэффициентами часто оказывается полезной следующая теорема: целые корни любого алгебраического равнения с целыми коэффициентами являются делителями свободного члена.

Докажем эту теорему: Пусть Z = k - целый корень равнения

a_n×Z^nа + a_nЦ1×Z^nЦ1 +...+ a₁×Z¹ + a₀ = 0

с целыми коэффициентами. Тогда

a_n×k^nа + a_nЦ1×k^nЦ1 +...+ a₁×k¹ + a₀ = 0

a₀ = - k(a_n×k^nЦ1 + a_nЦ1×k^nЦ2 +...+ a₁) Число в скобках, при сделанных предположениях, очевидно, целое, значит k - делитель числа a_0.

5. Связь комплексных чисел с геометрией на плоскости.

При заданной прямоугольной декартовой системе координат на плоскоснти комплексному числу z = x+iy (i²= -1) можно взаимно однозначно понставить в соответствие точку М плоскости с координатами х, у (рис.1):

.

Число z тогда называют комплексной координатой точки М.

Поскольку множество точек евклидовой плоскости находится во взаимнно однозначном соответствии с множеством комплексных чисел, то эту плоснкость называют также плоскостью комплексных чисел. Начало О декартовой системы координат называют при этом начальной или нулевой точкой плонскости комплексных чисел.

При у=0 число z действительное. Действительные числа изображаются точками оси х, поэтому она называется действительной осью. При х=0 число z чисто мнимое: z=iy. Мнимые числа изображаются точками оси у, поэтому она называется мнимой осью. Нуль - одновременно действительное и чисто мнимое число.

Paccтoяниe от начала О плоскости до точки М(z) называется модулем комплексного числа z и обозначаетнся |z| или r:

|z| = r = |OM| =

_аЕсли 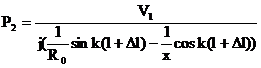Ч ориентированный гол, образованный вектором 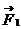с осью х, то по определению функции синуса и косинуса

откуда 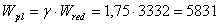аи поэтому .

Такое представление комплексного числа z называется его тригонометринческой формой. Исходное представление z=x+iy называют алгебраичеснкой формой этого числа. При тригонометрическом представлении гол 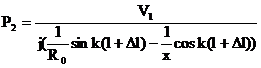аназывают аргументом комплексного числа и обозначают еще через arg z:

Если дано комплексное число z=x+iy, то число аназывается комплексно-сопряженным (или просто сопряженным) этому числу z. Тогда, очевидно, и число z сопряжено числу Точки М(z) и асимметричны относительно оси х (рис.2).

Из равенства y=0 и обратно. Это значит, что число, равнное своему сопряженному, является действительным и обратно.

Точки с комплексными координатами z и -z симметричны относительнно начальной точки О. Точки са комплексными координатами z и асимнметричны относительно оси у. Из равенства z=авытекает x=0 и обнратно. Поэтому словие z=аявляется критерием чисто мнимого числа.

Для любого числа z, очевидно, |z| = | = |-z| = |

Сумма и произведение двух сопряженных комплексных чисел являются действительными числами:а .

Число, сопряженное с суммой, произведением или же частным комплекснных чисел, есть соответственно сумма, произведение или же частное чисел, сопряженных данным комплексным числам:

Эти равенства можно легко проверить, пользуясь формулами для опенраций над комплексными числами._а

Каждой точке М(z) плоскости - взаимно однозначно соответствует векнтор . Поэтому комплексные числа можно интерпретировать векторами, приложенными к точке O. Сложению и вычитанию комплексных чисел отвечает сложение и вычитание соответствующих им векторов. Именно если и b - комплексные координаты точека A и В соответственно, то число с=а+b является координатой точки С, такой, что а(рис.3). Комплексному числу d=a-b соответствует такая точка D, что .

_аРасстояние между точками А и В равно

|АВ| = |а-b|. (1)

Так как |z|²= z, то

|AB|²=(a-b)( (2)

равнение z= r² определяет окружность с центром О радиуса r. Отношение в котором точка С делит данный отрезок АВ, выражается через комплексные координаты этих точек так:

откуд 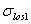(3)

Если положить аи а

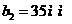(4)

Условия (4) необходимы и достаточны для того, чтобы точки А, В, С были коллинеарны.

При точк c является серединой отрезка AB, и обратно.

Тогда:

c = 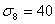. (4a)

Пусть имеем параллелограмм ABCD. Его центр имеет комплексную координату 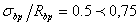а= апри словии, что точки А, В, С, D имеют соответственно комплексные координаты а, b, с, d. Если не исключать случай вырождения параллелограмма, когда все его вершины оказываются на одной прямой, то равенство

a+c = b+d (5)

является необходимым и достаточным словием того, чтобы четырехугольнник ABCD был параллелограммом.

5.2. Параллельность и перпендикулярность. Коллинеарность трех точек

ОПР: Пусть на плоскости комплексных чисел даны точки А(а) и B(b). Векторы 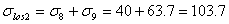аиасонаправлены тогда и только тогда, когда arg a = arg b, т. е. при arg - arg b=arg=0 (при вычитании комплексных чисел, из аргумента делимого вычитается аргумент делителя!).

Очевидно также, что эти векторы направлены противоположно в том и только в том случае, если arg a - arg b=arg_.

Комплексные числа с аргументами 0, 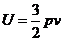являются действительными. ТЕОРЕМА (Критерий коллинеарности точек О, А, В): Для того чтобы точки А(а) и В(b) были коллинеарны с начальной точкой О, необходимо и достаточно, чтобы частное абыло действительным числом, т. е.

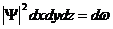аили (6)

Действительно, так как в этом случае число адействительное (k=), то кринтерий (6) эквивалентен такому:

(7)

Возьмем теперь точки A(а), B(b), C(c), D(d).

ОПР: Векторы аи аколлиннеарны тогда и только тогда, когда точки, определяемые комплексными числами Чb и сЧd, коллинеарны с началом О.

Замечание:

1. На основании (6) имеем:

(8)

2. Если точки А, В, С, D принадлежат единичной окружности l,то

и поэтому словие (8) принимает вид:

а; (9)

3. Коллинеарность точек A, В, С характеризуется коллинеарностью векнторов аи . Используя (8), получаем:

(10)

Это критерий принадлежности точек A, B, С одной прямой. Его можно представить в симметричнома виде

(11)

Если точки A и B принадлежат единичной окружности l, то 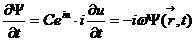, и поэтому каждое из соотношений (10) и (11) преобразуется (после сокращения на (а-b) в такое:

(12)

Точки А и В фиксируем, точку С будем считать переменной, переобознанчив ее координату через z. Тогда каждое из полученных соотношений (10), (11), (12) будет равнением прямой АВ:

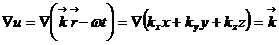, (10а)

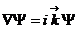. (12a)

В частности, прямая ОА имеет равнение

Переходим к выводу критериев перпендикулярности отрезков. Ясно, что

Комплексные числа с аргументам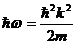и аи являются чисто мнимыми.

Поэтому,

или

(13)

Отрезки АВ и CD перпендикулярны тогда и только тогда, когда векторы точек с комплексными координатами Чb и сЧd перпендикулярны. В синлу (13) имеем:

(14)

В частности, когда точки А, В, С, D принадлежат единичной окружности l, то зависимость (14) упрощается:

(15)

Выведем уравнение касательной к единичной окружности l в ее точке

P(р). Если М (z) Ч произвольная точка этой касательной, то аи обратно. На основании (14) имеем:

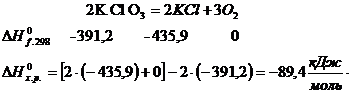
или

Поскольку , то уравнение касательной становится таким:

(16)

Это частный случай равнения (12a) при а=b=р. Решим еще две вспомогательные задачи, необходимые для решения содержательных геометрических задач.

5.3. ПРЯМАЯ И ОКРУЖНОСТЬ НА ПЛОСКОСИа КОМПЛЕКСНЫХ ЧИСЕЛ

Пусть произвольной точке М плоскости комплексных чисел соответнствует комплексное число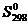. Из равенств 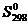аи аодннозначно выражаются декартовы координаты х и у точки М через комплекснные числа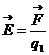

(1)

Поэтому комплексные числа z и аназываются сопряженными комплексными координатами этой точки.

Формулы (1) позволяют осуществить переход от равнения геометринческой фигуры в декартовых координатах к ее равнению в сопряженных комплексных координатах. Однако сейчас мы предпочли непосредственное рассмотрение равнений в сопряженных комплексных координатах.

Геометрический смысл равнения

Найдем множество точек плоскости, сопряженные комплексные координнаты которых удовлетворяют равнению

(2)

Сначала выделим особый случай, когда с=0. Тогда имеем систему отнонсительно аи

второе уравнение которой получается из первого переходом к сопряжеым числам. Уравнивая коэффициенты при , путем вычитания второго равнения из первого получаем:

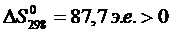
Если , т.е. 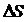абудет единственное число z=0. При ауравнение 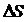анапишем в виде . Этому словию довлетнворяет каждая точка прямей m, проходящей через начало под глом 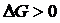ак действительной оси (рис.1). Так, равнениема

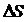(3)

задается прямая при аи точка апри .

Пусть теперь (2) можно всегда сделать действительным числом путем мнонжения обеих частей уравнения на с. Поэтому сразу будем полагать Тогда имеем систему:

из которой получаем: 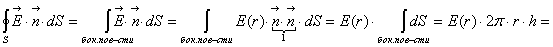. Рассмотрим возможные случаи.

Если , то аи подстановкой в исходное равнение получаем: аили

При аего решение единственно:

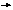
При арешений нет.

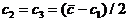
Если аи (2) при 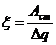апрямая. В самом деле, возьмем точку аи векнтор аточки В(b) и рассмотрим множество точека М(z), для каждой из конторых (MQ)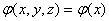OB):

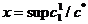(4)

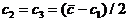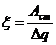Очевидно, это множество есть прямая. При аи ауравнение (4) эквивалентно уравнению (2).

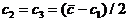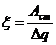Таким образом, при аи ауравнение (2) есть равнение прямой, которая проходит через точку аперпендикулярно вектору .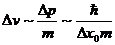

Наконец, отметим случай, когда 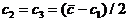, но . Тогда система

приводит к противоречию: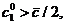

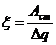
Подведем итоги. равнением a и b отличен от нуля, задается:

1) прямая при |а|=|b|, с=0, также при ;

2) единственная точка при ;

3) пустое множество в иных случаях, т. е. при |a| = |b|, такнже при 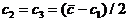, . ^а

Достигнув поставленной цели, возвратимся снова к системе:

не налагая ограничений на коэффициенты а, b, с, кроме того, что a и b не равны нулю одновременно. равнивая коэффициенты при , приходим к уравнению , которое:

) имеет единственное решение при ;

б) имеет бесконечное множество решений при аи ;

в) не имеет решений при аи .

Отсюда и на основании результата предыдущих исследований получаем, что равнение аопределяет:

) единственную точку при

б) прямую при аи ;

в) пустое множество при аи .

Уравнение

а(5)

прямой в сопряженных комплексных координатах будем называть приведеым равнением прямой.

5.4. Две прямые. Расстояние от точки до прямой

Пусть прямая т задана приведенным уравнением . Так как она перпендикулярна вектору абудет ей параллелен (рис.2). Следовательно, ориентированный угол от оси х до прямой т равен аргументу числа ai:

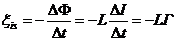
(6)

Положительно ориентированный гол 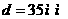аот прямойа адо прямой аравен глу между их направляющими векторами 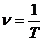аи :

. (7)

Формулы (6) и (7) позволяют находить соответствующие глы с точнностью до слагаемого .

Из формулы (7) вытекает критерий перпендикулярности и критерий параллельности прямых аи . В самом деле, ачисто мнинмое число. Это значит, что

(8)

Пр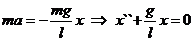и аили аполучаем:

(9)

Если прямая апроходит через точку 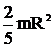аи ее равнение можно написать в виде:

(10)

В силу словия (8) перпендикулярности для прямой, перпендикулярнной данной, коэффициентами при, z и абудут соответственно числа и . Поэтому на основании равнения (10) получаем уравнение

(11)

прямой, проходящей через точку аперпендикулярно прямой 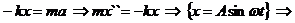Решение системы

дает координату

(12)

основания M₁ перпендикуляра, опущенного из точки ана прямую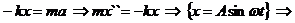

Так как расстояние d от точки M₀ этой прямой равно

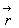. (13)

Геометрический смысл, равнения

Из формулы расстояния между двумя точками получается равнение окружности по ее центру S (s) и радиусу R :

(14)

Пусть дано равнение

, (15)

в котором на комплексные коэффициенты а, b, с не накладывается заранее никаких словий. Требуется найти множество точек, координаты которых ему довлетворяют. С этой целью добно представить его в эквивалентном виде:

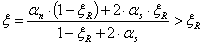(16)

Рассмотрим все возможные случаи для коэффициентов а, b, с.

1. Сравнивая равнение (16) с равнением (14) окружности, приходим к выводу, что равнение (16), значит, и равнение (15) задают окружность тогда и только тогда, когда 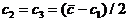аи abЧс - действительное число. Так как в этом случае с должно быть действительным числом.

Итак, уравнение

а(17)

есть равнение окружности с центром s=-b и радиусом .

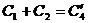2. При 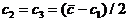с=ab равнению (16) удовлетворяет единственная точнка s=-b. В частности, этот случай имеет место при а=b=с=0. Соблюдая аналогию, говорят, что равнением азадается окружнность с центром s=-b нулевого радиуса.

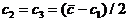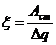
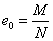3. Если , , то а- чисто мнимое число. Полагаем , тогда (16) можно записать так:

. а(18)

Уравнению (18) не довлетворяет ни одна точка плоскости, поскольку левая часть неотрицательна, правая отрицательна при любом значении z. Говорят, что это равнение есть равнение окружности мнимого радиуса iR с действительным центром S, имеющим комплексную координату s=-b.

4. Когда 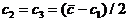, но , равнение (16) противоречиво: левая часть его действительна, правая нет. В этом случае оно не задает никакого геометринческого образа (даже мнимого!).

5. Осталось рассмотреть случай, когда . Тогда из уравнения (15) вычтем равнение 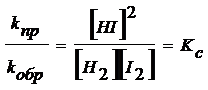, получающееся из (15) переходом к сопряженным комплексным числам. Получаем:

откуда

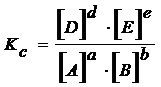
Выполняя эту подстановку в равнение (15), приводим его к виду

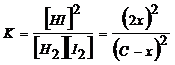(19)

При ауравнения (15) и (19) равносильны. В зависимости от того, отличен от нуля или равен нулю дискриминант

квадратного равнения (19), оно будет определять две различные (дейстнвительные!) или две совпавшие точки. При D=0 совпавшие точки имеют комплексную координату

В частности, при c=ab как равнение (16), так и равнение (19) дает панру точек z₁=-b и .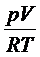

Итак, уравнением (15) задается либо окружность (действительная, мни мая, нулевого радиуса), либо две точки (различные или же совпавшие), либо пустое множество точек.

Рассмотрим одну замечательную пару окружностей.

Две пересекающиеся окружности называются ортогональными, если касательные к ним в их общей точке перпендикулярны. Тогда, очевидно, кансательная к одной из ортогональных окружностей в их общей точке содержит центр другой окружности.

Для того чтобы окружности (A, R) и (В, r) были ортогональны, необнходимо и достаточно, чтобы |AB|²=R²+r² , или

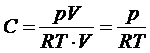(20)

Если окружности заданы равнениями

и

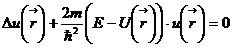
то (20) их ортогональности трансформируется так:

(21)