Читайте данную работу прямо на сайте или скачайте

Комплексные числа

Брянский городской лицей № 1

Учебно-исследовательская работа

по математике на тему:

Комплексные числа

Выполнил

ученик 10 физико-

математического класса

Петрухин Вячеслав

Учитель: Тюкачева О.И.

Брянск, 2003

Оглавление:

1.Комплексные числ 3

2.Свойства операций над комплексными числами 3

3. Комплексная плоскость 3

4. Модуль комплексного числ 4

5. Геометрический смысл сложения, вычитания и модуля разности двух комплексных чисел 5

6. Аргументы комплексного числ 5

7.Алгебраическая и тригонометрическая формы. комплексного числ 6

8. множение и деление комплексных чисел в тригонометрической форме 8

9. Возведение в степень и извлечение корня 8

10.Квадратные уравнения 10

11.Использованная литератур 14

В элементарной математике изучаются действительные числа. С начала в процессе счёта возникает так называемый натуральный ряд чисел 1, 2,Е n,Е В арифметике вводятся действия сложения и множения над натуральными числами. Что де касается операций вычитания и деления, то они же оказываются не всегда возможными во множестве натуральных чисел.

Та же потребность измерения величин и проведения таких операций, как извлечения корня, решение алгебраических равнений, приводит к дальнейшему расширению запаса рассматриваемых чисел: появляются иррациональные и, наконец, комплексные числа.

1.Комплексные числа

Комплексными числами называются выражения вида a + ib, где a и b - любые действительные числа, i - некоторый символ, для которых вводятся понятия равенства и операции сложения и множения:

) два комплексных числа a + ib и c + id равны тогда и только тогда, когда

a=c и b=d;

б) суммой чисел a + ib и c + id называется число

a + c + i(b +d);

в) произведением чисел a + ib и c + id называется число

ac - bd +i(ad+bc).

Комплексные числа принято обозначать одной буквой (чаще всего буквой z или w). Равенство z= a + ib означает, что комплексное число a + ib обозначено буквой z.

Действительное число a называется действительной частью комплексного числа z = a + ib и обозначается Re z; пишут Re z =a или Re z=aа или Re(a + ib) = a. Число b называется мнимой частью числа z= a +ib и обозначается Im z, пишут Im z = b или Im(a +ib) = b. Символ I называется мнимой единицей.

Заметим, что операции сложения и умножения над числами a+ i0 проводятся так же, как над действительными числами.

Таким образом, отождествив число a + i0 с действительным числом a, получим, что каждое действительное число содержится во множестве комплексных чисел, именно a =a+i0.

Числа вида 0 +ib называю чисто мнимыми и обозначаются ib.

На основании формулы (2) найдём значение выражения i²=ii:

i² = ii =(0+i1)(0+i1)= -1+i0=-1.

Таким образом,

i²=-1.

2.Свойства операций над комплексными числами.

1.          Коммутативность сложения: z₁ + z₂ = z₂ + z₁.

2.          Ассоциативность сложения (z₁ + z₂)+z₃ = z₁ +(z₂ + z₃)

3.          z+0=z.

4.          Коммутативность множения: z₁ z₂= z₂ z₁.

5.          Ассоциативность множения: z₃₍ z₁ z₂) =z₁₍ z₂ z₃).

6.          Дистрибутивный закон: z₁₍ z₂ + z₃) =z₁ z₂ + z₁ z₃.

7.          1*z=z.

8.          z₁ и z₂, где z₁, существует такое число z

такое, что z₁z = z₂. Это число называется частным комплексных чисел z₁ и z₂ и обозначается а.Деление на 0 невозможно.

y

M(a;b) z = a +ib

x

0

a

b

а 3. Комплексная плоскость. Рассмотрим прямоугольную систему координат на плоскости. Каждому комплексному числу z = a + ib поставим в соответствие точку M(a,b) координатной плоскости, т.е. точку, абсцисса которой равна Re z = a, ордината равна Im z = b. Обратно, каждой точке плоскости с координатами (a,b) поставим в соответствие комплексное число z = a + ib.Сама координатная плоскость называется при этом комплексной плоскостью. Ось абсцисс называется действительной осью, ось ординат - мнимой.

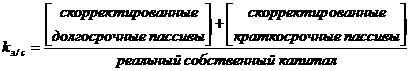
Не менее важной и добной является интерпретация комплексного числа a + ib как вектор .

4. Модуль комплексного числа. Модулем комплексного

числа z = a +ib называется длина вектора, соответствующего

этому числу. Модуль обозначается аили буквой r. Применяя

теорему Пифагора, получим, что а=_.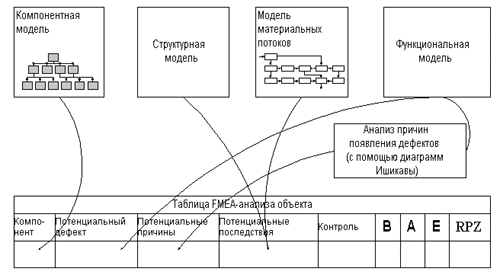

Пусть z = a +ib. Число a - ib называется комплексно сопряжённым с числом z = a +ib и обозначается а= a - ib. Заметим, что = =, z² + b²=² =²,

Пример 1. Запишите z в алгебраической форме, если

)

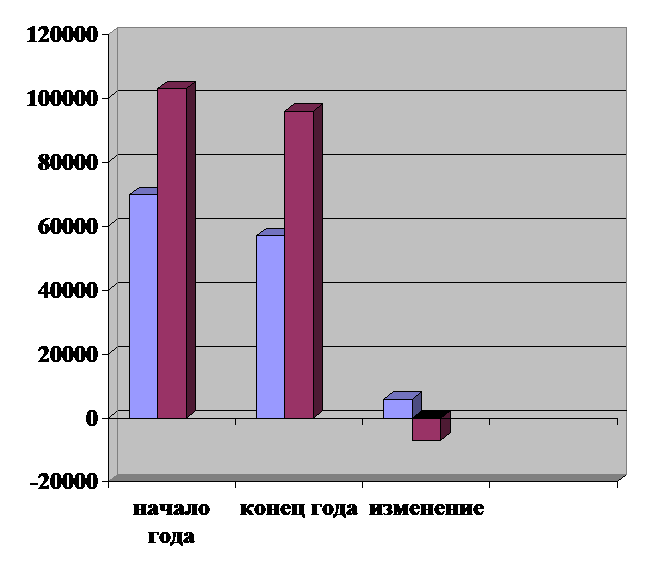
б)

Пример 2. Запишите решения системы

)а б)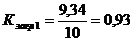

в алгебраической форме.

Решение:

)

б)

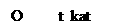а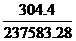

Пример 3.Существуют ли такие действительные числ x и y, для которых числа z₁ и z₂ являются сопряжёнными

) z₁=8x² - 20i¹⁵, z₂=9x² - 4+ 10yi³;

б)z₁=4x + y+(1+I)y, z₂=8 + ix.

Решение:

) z₁=8x² - 20i¹⁵=8x² + 20i; z₂=9x² - 4+ 10yi³=9x² - 4 - 10yi;

Используя определение сопряжённых комплексных чисел, получим систему:

откуда такие сопряжённые числ существуют.

б)z₁=4x + y + (1+i)y = 4x +2y+yi;

z₂=8+ix.

Используя определение сопряжённых комплексных чисел, получим систему:

аоткуда такие сопряжённые числ существуют.

5. Геометрический смысл сложения, вычитания и модуля разности двух комплексных чисел.

z1

M1

y

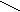
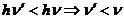
z₁=a₁ + ib₁ и z₂=a₂ + ib₂.Им соответствуют векторы с координатами (a₁,b₁) и (a₂,b₂). Тогда числу z₁+z₂=a₁ + a₂ + i(b₁ + b₂) будет соответствовать вектор с координатами (a₁ + a₂,b₁+b₂).Таким образом, чтобы найти вектор, соответствующий сумме комплексных чисел z₁ и z₂, надо сложить векторы, отвечающие комплексным числам z₁ и z₂.

z2-z1

M

z2

-z1

M

M2

x

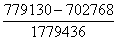
z₁- z ₂ комплексных чисел z₁ и z₂ соответствует разность векторов, Соответствующих числам z₁ и z₂.Модуль адвух комплексных чисел z₁ и z₂ по определению модуля есть длина вектора z₁- z ₂.Построим вектор, как сумму двух векторов z₂ и (- z₁). Получим вектор , равный вектору .Следовательно, аесть длина вектора ,то есть модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.

b

z=a+ ib

y

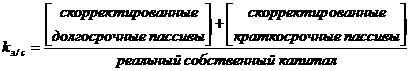
6. Аргументы комплексного числа. Аргументом комплексного числа z= a + ib z; величина гла считается положительной если отсчет производится против часовой стрелки, и отрицательной, если отсчет производится по часовой стрелке.

Для обозначения того факта, что число j является аргументом числа z= a+ ib, пишут j=arg z или j=arg (a+ib).

j-2p

a

j

x

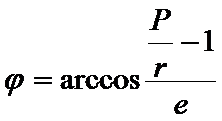z=0 аргумент не определяется. Поэтому во всех последующих рассуждениях, связанных с понятием аргумента будем считать, чтоz=0 Ц единственное число, которое определяется заданием только его модуля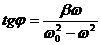

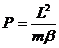
С другой стороны, если задано комплексное число, то, очевидно, модуль этого числа всегда определён единственным образом в отличие от аргумента, который всегда определяется неоднозначно: если j - некоторый аргумент числа z,то глы j+2pk, 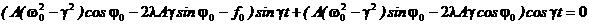z.

Из определения тригонометрических функций следует, что если j=arg (a+ib),то имеет место следующая система

аили

Пример 4. Сколько решений имеет система равнений

)аб) в)

Решение:

1

i

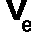
найдём модуль1-i:а .

Заметим, что никакая точка большей окружности не

приближена к меньшей на расстояние, равное

i

1

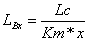
i только одной точки меньшей окружности мы получаем что эта точка попадает на

другую окружность.

i

корень

корни

	1

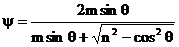
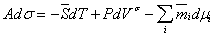
7.Алгебраическая и тригонометрическая формы комплексного числа. Запись комплексного числа z в виде a +ib называется алгебраической формой комплексного числа.

Рассмотрим другие формы записи комплексных чисел. Пусть r- модуль, j - какой-либо из аргументов комплексного числа z= a+ ib, то есть r = j=arg (a+ib). Тогда из формулы (5) следует, что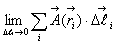

Запись комплексного числа в виде тригонометрической формой.

Для того чтобы перейти от алгебраической формы комплексного числа a+ib к тригонометрической, достаточно найти его модуль и один из аргументов.

Пример 5. Какое множество точек комплексной плоскости задаётся словием

)

б)

в)

)

д)

1

i

1

i

б)

iа и вправо на 1 поучались бы равноудалёнными от начала координат, откуда

чтобы построить множество точек, довлетворяющих данному словию, мы должны:

1)     

2)      а влево и на i вверх

в)

а -i чем к 2i, эти точки казаны на рисунке.

ip/3 i

p/3

i

г)

1

д)

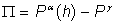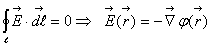
а это будут точки далённые от начала координат не более чем на 1 и при этом исключая число 0. учитывая второе и третье словие, получим:

е)

е) Чтобы построить точки, довлетворяющие первому условию, надо сдвинуть точки, далённые на расстояние 1,

на 1 вправо. При этом, учитывая другие словия, получим

искомое множество точек.

Пример 6. Будет ли тригонометрической формой числа

)

б)

в)

Решение:

Тригонометрической формой записи числа атолько будет выражение а), так как только оно довлетворяет определению тригонометрической формы записи числа(

8. множение и деление комплексных чисел в тригонометрической форме. Пусть

Тогда

модуль и произведение двух комплексных чисел равен произведению модулей сомножителей, сумма аргументов сомножителей является аргументом произведения.

Пусть

Таким образом, модуль частного двух комплексных чисел равен частному модулей делимого и делителя, разность аргументов делимого и делителя является аргументом частого.

9. Возведение в степень и извлечение корня. Формула (6) для произведения двух комплексных чисел может быть обобщен на случай

а

Отсюда, как частный случай, получается формула, дающая правило возведение комплексного числа 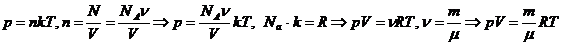ав целую положительную степень:

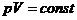а (8)

Таким образом, при возведении комплексного числа в степень с натуральным показателем его модуль возводится в степень с тем же показателем, аргумент множается на показатель степени.

Формула (8) называется формулойа Муавра.

Число аиз числа w (обозначается

Если w=0, то при любом n равнение z=0.

Пусть теперь z и w в тригонометрической форме:

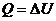
Тогда равнение апримет вид

Два комплексных числа равны тогда и только тогда, когда равны их модули, аргументы отличаются на число, кратное 2p. Следовательно,

или

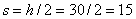
Таким образом, все решения уравнения

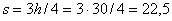
В самом деле, придавая числу k в формуле (9)целые значения, отличные от 0, 1, Е, (n-1), мы не получаем других комплексных чисел.

Формула (9) называется второй формулой Муавра.

Таким образом, если n корней степени n из числа w: все они содержатся в формуле(9).

В частности, если а равнение аимеет два корня:

то есть эти корни симметричны относительно начала координат.

Также из формулы (9) нетрудно получить, что еслиn-угольника, вписанного в окружность с центром в точке z=0 и радиусом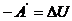

Из сказанного выше следует, что символ i и-i,или одно, и, если одно, то какое именно.

Пример 7. Запишите в тригонометрической форме:

)

б)

в)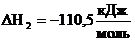

Решение:

)

б) Так как

Так как

в) Так как

10.Квадратные равнения. В школьном курсе алгебры рассматривались квадратные равнения

(10)

с действительными коэффициентами a, b, c. Там было показано, что если дискриминант равнения (10) неотрицателен, то решения такого равнения даются формулой

(11)

В случае, если

Для вывода формулы (11) использовался приём выделения квадрата трёхчлена с последующим разложением левой части на линейные множители:

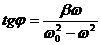
откуда и получалась формула (11). Очевидно, что все эти выкладки остаются справедливыми и в том случае, когда a, b, c являются комплексными числами, корни равнения отыскиваются во множестве комплексных чисел.

Таким образом, во множестве комплексных чисел равнение

всегда разрешимо. Если

где под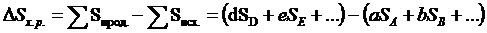аподразумеваются все значения корня.

Пример 8. Решить уравнение

)

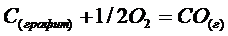
б)

Решение:

) Данное равнение является квадратным.

По формуле корней квадратного уравнения имеем:

Для определения всех значений аположим

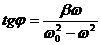
Тогда

и, следовательно, x и y довлетворяют системе

причём x и y действительные числа. Решим систему:

Заметим, что x=0 решением системы не является.

При :

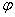
Решим равнение (*): x⁴+15x²-16=0 Цквадратное равнение относительно x², откуда

Вернёмся к системе:

Поэтому

б) Данное равнение является квадратным.

По формуле корней квадратного уравнения имеем:

Для определения всех значений аположим

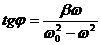
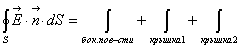
Тогда

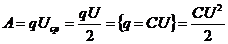
и, следовательно, x и y довлетворяют системе

причём x и y действительные числа. Решим систему:

Заметим, что x=0 решением системы не является.

При :

Решим равнение (*): x⁴-16x²-225=0 Цквадратное равнение относительно x², откуда

Вернёмся к системе:

Поэтому

Пример 9. Решить уравнение

)

б)

Решение:

) Пусть

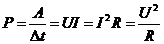
Возвращаясь к z, получим

1) а вторую формулу Муавра, получим:

1) а вторую формулу Муавра, получим:

Следовательно,

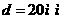
2) а вторую формулу Муавра, получим:

Следовательно,

б)Преобразуем уравнение:

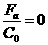
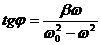
Заметим, что а вторую формулу Муавра, получим:

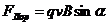
Пример10. Решите равнение:

Решение:

Решим уравнение как квадратное относительно z²: D=

Пусть z=a+ib, тогда

Пусть

Пусть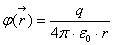

Ответ:

Использованная литература:

1. Пособие по математике для поступающих в вузы: пособие/ Кутасов А.Д., Пиголкина Т.С., Чехлов В.И., Яковлев Т.Х. - под редакцией Яковлева Г.Н.-3-е издание М.: Наука, 1998, Глава X.
2. Лекции и задачи по элементарной математике / Болтянский В.Г., Сидоров Ю.В., Шабунин М.И., - М.: Наука, 1971. ГлаваIV.