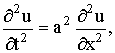Читайте данную работу прямо на сайте или скачайте
Использование дифференциальных равнений в частных производных для моделирования реальных процессов
Министерство общего и профессионального образования
Сочинский государственный ниверситет туризма
и курортного дела
Педагогический институт
Математический факультет
Кафедра общей математики
ДИПЛОМНАЯ РАБОТА
Использование дифференциальных равнений в частных производных для моделирования реальных процессов.
|
дневной формы обучения
Специальность 010100
Математика
Прокофьевой Я. К.
Студенческий билет № 95035
|
техн. наук
Позин П.А.
Сочи, 2 г.
СОДЕРЖАНИЕ
Введени..ЕЕ3
Глава 1. равнения гиперболического типа.
з1.1. Задачи, приводящие к равнениям гиперболического типа..5
1.1.1. равнение колебаний струны..5
1.1.2. равнение электрических колебаний в проводахЕЕ.8
з1.2. Метод разделения переменных..10
1.2.1. равнение свободных колебаний струныЕ.10
Глава 2. равнения параболического типа.
з2.1. Задачи, приводящие к равнениям параболического типа..17
2.1.1. равнение распространения тепла в стержне..17
2.1.2. Распространение тепла в пространстве.19
з2.2. Температурные волны..23
Глава 3. Моделирование с помощью дифференциальных равнений в частных производных.
з3.1. Дифракция излучения на сферической частиц29
Заключени.40
Литература..41
ВВЕДЕНИЕ
Изучением дифференциальных уравнений в частных производных занимается математическая физика. Основы теории этих равнений впервые были изложены в знаменитом Интегральном исчислении Л. Эйлера.
Классические уравнения математической физики являются линейными. Особенность линейных уравнений состоит в том, что если U и V - два решения, то функция aU + bV при любых постоянных a и b снова является решением. Это обстоятельство позволяет построить общее решение линейного дифференциального равнения из фиксированного набора его элементарных решений и прощает теорию этих равнений.
Современная общая теория дифференциальных равнений занимается главным образом линейными уравнениями и специальными классами нелинейных равнений. Основным методом решения нелинейных дифференциальных равнений в частных производных выступает численное интегрирование.
Круг вопросов математической физики тесно связан с изучением различных физических процессов. Сюда относятся явления, изучаемые в гидродинамике, теории пругости, электродинамике и т.д. Возникающие при этом математические задачи содержат много общих элементов и составляют предмет математической физики.
Постановка задач математической физики, будучи тесно связанной с изучением физических проблем, имеет свои специфические черты. Так, например, начальная и конечная стадии процесса носят качественно различный характер и требуют применения различных математических методов.
Круг вопросов, относящихся к математической физике, чрезвычайно широк. В данной работе рассматриваются задачи математической физики, приводящие к равнениям с частными производными.
Расположение материала соответствует основным типам равнений. Изучение каждого типа уравнений начинается с простейших физических задач, приводящих к равнениям рассматриваемого типа.
Глава 1. РАВНЕНЯа ГИПЕРБОЛИЧЕСКООа ТИПА
з1.1. Задачи, приводящие к равнениям гиперболического типа.
Уравнения с частными производными 2-го порядка гиперболического типа наиболее часто встречаются в физических задачах, связанных с процессами колебаний. Простейшее равнение гиперболического типа

называется волновым равнением. К исследованию этого равнения приводит рассмотрение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводе, крутильных колебаний вала, колебаний газа и т.д.
1.1.1. Уравнение колебаний струны.
В математической физике под струной понимают гибкую, пругую нить. Напряжения,
возникающие в струне в любой момент времени, направлены по касательной к ее профилю. Пусть струна длины  ав начальный момент направлена по отрезку оси Оx от 0 до
ав начальный момент направлена по отрезку оси Оx от 0 до 

Будем рассматривать малые отклонения точек струны от начального положения. В силу этого можно предполагать, что движение точек струны происходит перпендикулярно оси Ox и в одной плоскости. При этом предположении процесс колебания струны описывается одной функцией 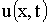 x в момент t.
x в момент t.
|
u |
|
x |
|
0 |
|
M |
|
M1 |
|
M2 |
|
x |
|
x1 |
|
x2 |
 |
Рис. 1.1.
Так как мы рассматриваем малые отклонения струны в плоскости 
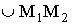 аравняется ее проекции на ось Ox, т.е.
аравняется ее проекции на ось Ox, т.е.  1 Также будем предполагать, что натяжение во всех точках струны одинаковое; обозначим его через Т.
1 Также будем предполагать, что натяжение во всех точках струны одинаковое; обозначим его через Т.
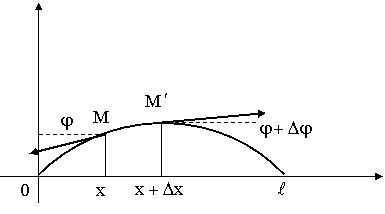
Рассмотрим элемент струны 
|
x |
|
M |
|
0 |
 |
|||
|
|||
Рис. 1.2.
На концах этого элемента, по касательным к струне, действуют силы Т. Пусть касательные образуют с осью Ox глы  Ou сил, действующих на элемент
Ou сил, действующих на элемент 

 амал, то можно положить
амал, то можно положить


(здесь мы применили теорему Лагранжа к выражению, стоящему в квадратных скобках).
Чтобы получить равнение движения, нужно внешние силы, приложенные к элементу,
приравнять силе инерции. Пусть 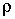 а- линейная плотность струны. Тогда масса элемента струны будет
а- линейная плотность струны. Тогда масса элемента струны будет 
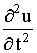
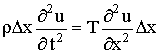
Сокращая на
 аи обозначая
аи обозначая 
 (1)
(1)
Это и есть волновое равнение - равнение колебаний струны. Для полного определения движения струны одного равнения (1)
недостаточно. Искомая функция  адолжна довлетворять еще граничным словиям, казывающим, что делается на концах струны
адолжна довлетворять еще граничным словиям, казывающим, что делается на концах струны  t = 0).
Совокупность граничных и начальных словий называется краевыми словиями.
t = 0).
Совокупность граничных и начальных словий называется краевыми словиями.
Пусть, например, как мы предполагали, концы струны при  анеподвижны. Тогда при любом t должны выполнятся равенства:
анеподвижны. Тогда при любом t должны выполнятся равенства:
 (Т)
(Т)
 (ТТ)
(ТТ)
Эти равенства являются граничными словиями для нашей задачи.
В начальный момент t = 0 струна имеет определенную форму, которую мы ей придали. Пусть эта форма определяется функцией f (x). Таким образом, должно быть
 (Т)
(Т)
Далее, в начальный момент должна быть задана скорость в каждой точке струны, которая определяется функцией 
 (ТТ)
(ТТ)
Условия (Т) и (ТТ) являются начальными словиями.
Замечание. В частности, может быть  аили
аили 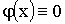
 аи
аи 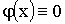

1.1.2. равнение электрических колебаний в проводах.
Как казывалось выше, к уравнению (1) приводит и задача об электрических колебаниях в проводах.
Электрический ток в проводе характеризуется величиной i (x, t) и напряжением v (x, t), которые зависят от координаты x точки провода и от времени t. Рассматривая элемент провода 
 аравно
аравно 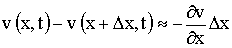
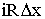

 (4)
(4)
где R
и L - сопротивление и коэффициент индуктивности, рассчитанные на единицу длины провода. Знак минус взят потому, что ток течет в направлении, обратном возрастанию v. Сокращая на 
 (5)
(5)
Далее, разность токов, выходящего из элемента  аи входящего в него за время
аи входящего в него за время 

Она расходуется на зарядку элемента, равную 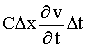
 а(здесь А - коэффициент утечки). Приравнивая эти выражения и сокращая на
а(здесь А - коэффициент утечки). Приравнивая эти выражения и сокращая на 
 (6)
(6)
Уравнения (5) и (6)принято называть телеграфными равнениями.
Из системы равнений (5) и (6) можно получить равнение, содержащее только искомую функцию i (x, t), и уравнение, содержащее только искомую функцию v (x, t). Продифференцируем члены уравнения (6) по x; члены равнения (5) продифференцируем по t и множим их на С. Произведя вычитание, получим:

Подставляя в последнее равнение выражение  аиз равнения (5),
получим:
аиз равнения (5),
получим:

или
 (7)
(7)
налогичным образом получается равнение для определения v (x, t):
 (8)
(8)
Если пренебречь течкой через изоляцию  аи сопротивлением
аи сопротивлением 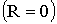

где обозначено: 
з1.2. Метод разделения переменных.
1.2.1. Уравнение свободных колебаний струны.
Метод разделения переменных или метод Фурье, является одним из наиболее распространенных методов решения равнений с частными производными. Изложение этого метода мы проведем для задачи о колебаниях струны, закрепленной на концах. Итак, будем искать решение равнения
удовлетворяющее однородным граничным словиям
 (9)
(9)
и начальным словиям
 (10)
(10)
Уравнение (1) линейно и однородно, поэтому сумма частных решений также является решением этого равнения. Имея достаточно большое число частных решений, можно попытаться при помощи суммирования их с некоторыми коэффициентами найти искомое решение.
Поставим основную вспомогательную задачу: найти решение равнения
не равное тождественно нулю, довлетворяющее однородным граничным словиям
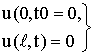 (11)
(11)
и представимое в виде произведения
 (12)
(12)
где X (x) - функция только переменного x, T (t) - функция только переменного t.
Подставляя предполагаемую форму решения (12) в равнение (1), получим:

или, после деления на XT,
 (13)
(13)
Чтобы функция (12) была решением равнения (1), равенство
(13) должно довлетворяться тождественно, т. е. 0 Л х Л  t Ы 0.
Правая часть равенства (13) является функцией только переменного t, левая - только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части равенства (13) при изменении своих аргументов сохраняют постоянное значение
t Ы 0.
Правая часть равенства (13) является функцией только переменного t, левая - только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части равенства (13) при изменении своих аргументов сохраняют постоянное значение
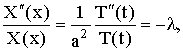 (14)
(14)
где
 Ц постоянная, которую для добства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке.
Ц постоянная, которую для добства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке.
Из соотношения (14) получаем обыкновенные дифференциальные уравнения для определения функций X (x) и T (t)
 (15)
(15)
 (16)
(16)
Граничные словия (11) дают:

Отсюда следует, что функция X (x) должна довлетворять дополнительным словиям:
X(0) = X( ) = 0, (17)
) = 0, (17)
Так как иначе мы имели бы

в то время как задача состоит в нахождении нетривиального решения. Для функции T (t) в основной вспомогательной задаче никаких дополнительных словий нет.
Таким образом, в связи с нахождением функции X (x) мы приходим к простейшей задаче о собственных значениях:
найти те значения параметра 
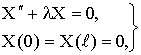 (18)
(18)
также найти эти решения. Такие значения параметра  аназываются собственными значениями, соответствующие им нетривиальные решения - собственными функциями задачи (18). Сформулированную таким образом задачу часто называют задачей Штурма - Лиувилля.
аназываются собственными значениями, соответствующие им нетривиальные решения - собственными функциями задачи (18). Сформулированную таким образом задачу часто называют задачей Штурма - Лиувилля.
Рассмотрим отдельно случаи, когда параметр  аотрицателен, равен нулю или положителен.
аотрицателен, равен нулю или положителен.
1.
При  Л 0 задача не имеет нетривиальных решений. Действительно, общее решение равнения (15) имеет вид
Л 0 задача не имеет нетривиальных решений. Действительно, общее решение равнения (15) имеет вид

Граничные словия дают:
Х (0) = С1 + С2 = 0;

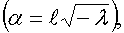
т. е.

Но в рассматриваемом случае  Ц действительно и положительно, так что
Ц действительно и положительно, так что 
С1 =0, С2 = 0
и, следовательно,
Х (х)
2.
При  а= 0 также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения (15) имеет вид
а= 0 также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения (15) имеет вид
Х (х) = С1х + С2.
Граничные условия дают:

т. е. С1 = 0 и С2 = 0 и, следовательно,
Х (х)
3.
При  Ы 0 общее решение уравнения может быть записано в виде
Ы 0 общее решение уравнения может быть записано в виде

Граничные условия дают:

Если Х(х) не равно тождественно нулю, то D2
 (19)
(19)
или

где n- любое целое число. Следовательно, нетривиальные решения задачи (18) возможны лишь при значениях

Этим собственным значениям соответствуют собственные функции

где Dn - произвольная постоянная.
Итак, только при значениях 
 (20)
(20)
существуют нетривиальные решения задачи (11)
 (21)
(21)
определяемые с точностью до произвольного множителя, который мы положили равным единице.
Этим же значениям  n
соответствуют решения равнения (9)
n
соответствуют решения равнения (9)
 (22)
(22)
где An и Bn - произвольные постоянные.
Возвращаясь к задаче (1), (9), (10), заключаем, что функции
 а (23)
а (23)
являются частными решениями равнения (1), довлетворяющими граничным словиям (11) и представимыми в виде произведения (12) двух функций, одна из которых зависит только от х, другая - от t. Эти решения могут довлетворить начальным словиям (10) нашей исходной задачи только для частных случаев начальных функций j(x) и y(x).
Обратимся к решению задачи (1), (9), (10) в общем случае. В силу линейности и однородности равнения (1) сумма частных решений
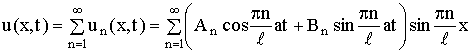 (24)
(24)
также удовлетворяет этому равнению и граничным словиям (9). Начальные словия позволяют определить An и Bn. Потребуем, чтобы функция (24) удовлетворяла словиям (10)
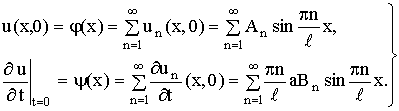 (25)
(25)
Из теории рядов Фурье известно, что произвольная кусочно-непрерывная и кусочно-дифференцируемая функция f(x), заданная в промежутке 
 (26)
(26)
где
 (27)
(27)
Если функции j(x) и y(x) довлетворяют словиям разложения в ряд Фурье, то
 (28)
(28)
 (29)
(29)
Сравнение этих рядов с формулами (25) показывает, что для выполнения начальных словий надо положить
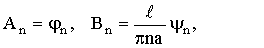 (30)
(30)
чем полностью определяется функция (24), дающая решение исследуемой задачи.
Итак, мы доказали, что ряд (24), где коэффициенты An и Bn определены по формуле (30), если он допускает двукратное почленное дифференцирование, представляет функцию u (x, t), которая является решением равнения (1) и удовлетворяет граничныма и начальным условиям (9) и (10).
Замечание. Решая рассмотренную задачу для волнового равнения другим методом, можно доказать, что ряд (24) представляет решение и в том случае, когда он не допускает почленного дифференцирования. При этом функция  должна быть дважды дифференцируемой,
должна быть дважды дифференцируемой,  а- один раз дифференцируемой.
а- один раз дифференцируемой.
Глава 2. РАВНЕНЯа ПАРАБОЛИЧЕСКООа ТИПА
з2.1. Задачи, приводящие к равнениям гиперболического типа.
2.1.1. Уравнение распространения тепла в стержне.
Рассмотрим однородный стержень длины 
Расположим ось Ох так, что один конец стержня будет совпадать с точкой х = 0, другой - с точкой х = 
|
0 |
|
x1 |
|
x2 |
 |
Рис. 2.1.
Пусть u (x, t) - температура в сечении стержня с абсциссой х в момента t. Опытным путем становлено, что скорость распространения тепла, т. е. количество тепла, протекающего через сечение с абсциссой х за единицу времени, определяется формулой
 (1)
(1)
где S - площадь сечения рассматриваемого стержня, k - коэффициент теплопроводности.
Рассмотрим элемент стержня,
заключенный между сечениями с абсциссами х1 и х2 (х2
Ц х1 =  1
за время
1
за время 
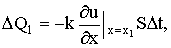 (2)
(2)
то же самое с абсциссой х2:
 (3)
(3)
Приток  1 -
1 -  Q2 в элемент стержня за время
Q2 в элемент стержня за время 
 (4)
(4)
Этот приток тепла за время 


или
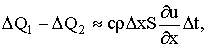 (5)
(5)
где с - теплоемкость вещества стержня, 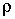 Ц плотность вещества стержня (
Ц плотность вещества стержня (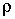

Приравнивая выражения (4) и
(5) одного и того же количества тепла 
|

Это и есть равнение распространения тепла (уравнение теплопроводности) в однородном стержне.
Чтобы решение равнения (6)
было вполне определено, функция u (x, t)а должна довлетворять краевым словиям, соответствующим физическим условиям задачи. Краевые словия для решения равнения (6) могут быть различные. словия, которые соответствуют так называемой первой краевой задаче для 
u (x, 0) = φ(x), (7)
u (0, t) = ψ1(t), (8)
u ( , t) = ψ2(t). (9)
, t) = ψ2(t). (9)
Физическое словие (7)
(начальное словие) соответствует тому, что при  ав разных сечениях стержня задана температура, равная φ(x). словия (8) и (9) (граничные условия) соответствуют тому, что на концах стержня при х = 0 и при х =
ав разных сечениях стержня задана температура, равная φ(x). словия (8) и (9) (граничные условия) соответствуют тому, что на концах стержня при х = 0 и при х =  аподдерживается температура, равная ψ1(t) и ψ2(t)
соответственно.
аподдерживается температура, равная ψ1(t) и ψ2(t)
соответственно.
Доказывается, что равнение
(6) имеет единственное решение в областиа
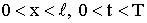
2.1.2. Распространение тепла в пространстве.
Рассмотрим процесс распространения тепла в трехмерном пространстве. Пусть u (x, y, z, t) - температура в точке с координатами (x, y, z) с момент времени t. Опытным путем установлено, что скорость прохождения тепла через площадку  а
(1))
а
(1))
 (10)
(10)
где k - коэффициент теплопроводности рассматриваемой среды, которую мы считаем однородной и изотропной, n - единичный вектор, направленный по нормали к площадке 

где  Ц направляющие косинусы вектора n, или
Ц направляющие косинусы вектора n, или

Подставляя выражение  ав формулу (10),
получаем:
ав формулу (10),
получаем:
 Q = -k n grad u
Q = -k n grad u  s.
s.
Количество тепла, протекающего за время ∆t через площадку ∆s, будет равно:
 Q
Q t = -k n grad u
t = -k n grad u  t
t  s.
s.
Вернемся к поставленной задаче. В рассматриваемой среде выделим малый объем V, ограниченный поверхностью S. Количество тепла, протекающего через поверхность S, будет равно:
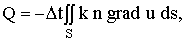 (11)
(11)
где n - единичный вектор, направленный по внешней нормали к поверхности S. Очевидно,
что формула (11) дает количество тепла, поступающего в объем V (или ходящего из объема V) за время 
Рассмотрим элементарный объем 




где с - теплоемкость вещества, ρ - плотность. Общее количество тепла, затраченное на повышение температуры в объеме V за время 

Но это есть тепло,
поступающее в объем V за время 

Сокращая на

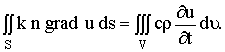 (12)
(12)
Поверхностный интеграл,
стоящий в левой части этого равенства, преобразуем по формуле Остроградского (в векторной форме, где F - дивергенция векторного поля,  Ц замкнутая поверхность)
Ц замкнутая поверхность)

полагая F = k grad u:

Заменяя двойной интеграл, стоящий в левой части равенства (12), тройным интегралом, получим:
|
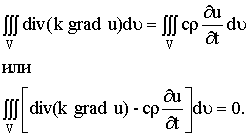
Применив теорему о среднем к тройному интегралу, стоящего слева, получим :
 (14)
(14)
где P (x, y, z) - некоторая точка объема V.
Так как мы можем выделить произвольный объем V в трехмерном пространстве, где происходит распространение тепла, и так как мы предполагаем, что подынтегральная функция в равенстве (13) непрерывна, то равенство (14) будет выполняться в каждой точке пространства. Итак,
 (15)
(15)
Но

Подставляя в равнение (15), получаем:
 (16)
(16)
Если k - постоянное, то

и равнение (15) в этом случае дает:

или,
положив 
 (17)
(17)
Коротко равнение (17) записывается так:
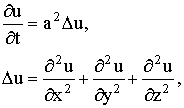
где  теплопроводности в пространстве. Для того чтобы найти единственное решение, отвечающее поставленной задаче, нужно задать краевые словия.
теплопроводности в пространстве. Для того чтобы найти единственное решение, отвечающее поставленной задаче, нужно задать краевые словия.
Пусть имеем тело 
 начальное условие:
начальное условие:
u (x, y, z, 0) =а φ (x, y, z). (18)
Кроме того, должна быть известна температура в любой точке М поверхности  атела в любой момент времени t - граничное словие:
атела в любой момент времени t - граничное словие:
u (М, t) =а ψ (М, t). (19)
(Возможны и другие граничные словия.)
Если искомая функция u (x, y, z, t) не зависит от z, что соответствует тому, что температура не зависит от z, то получаем равнение:
 (20)
(20)
- уравнение распространения тепла на плоскости. Если рассматривается распространения тепла в плоской области D с границей С, то граничные словия, аналогично (18) и (19), формулируются так:
u (x, y, 0) = φ (x, y),
u (М, t) = ψ (М, t),
где φ и ψ - заданные функции, М - точка границы С.
Если же функция u не зависит ни от z, ни от y, то получаем равнение

- равнение распространения тепла в стержне.
з2.2. Температурные волны.
Задача о распространении температурных волн в почве является одним из первых примеров приложения математической теории теплопроводности, развитой Фурье, к изучению явлений природы.
Температура на поверхности земли носит, как известно, ярко выраженную суточную и годовую периодичность. Обратимся к задаче о распространении периодических температурных колебаний в почве, которую будем рассматривать как однородное полупространство 
найти ограниченное решение равнения теплопроводности
 (1)
(1)
удовлетворяющее условию
u (0, t) = A cos  (2)
(2)
Предполагается, что функции u (x, t) и m (t) ограничены всюду, т.е.

Запишем граничное словие в виде
 (Т)
(Т)
Из линейности равнения теплопроводности следует, что действительная и мнимая части некоторого комплексного решения равнения теплопроводности каждая в отдельности довлетворяет тому же решению.
Если найдено решение равнения теплопроводности, довлетворяющее словию (Т), то его действительная часть удовлетворяет словию (2), мнимая - словию

Итак, рассмотрим задачу:
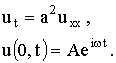 (3)
(3)
Ее решение будем искать в виде
 (4)
(4)
где  аи
аи  а- неопределенные пока постоянные.
а- неопределенные пока постоянные.
Подставляя выражение (4) в уравнение (3) и граничное словие, находим:
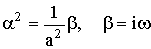
откуда

Для u (x, t) имеем:
 (5)
(5)
Действительная часть этого решения
 (6)
(6)
удовлетворяет равнению теплопроводности и граничному словию (2). Формула (6) в зависимости от выбора знака определяет не одну, две функции. Однако только функция, соответствующая знаку минус, довлетворяет требованию ограниченности. Таким образом, решение поставленной задачи получаем в виде
 (7)
(7)
На основании полученного решения можно дать следующую характеристику процесса распространения температурной волны в почве. Если температура поверхности длительное время периодически меняется, то в почве также станавливаются колебания температуры с тем же периодом, причем:
1.Амплитуда колебаний экспоненционально бывает с глубиной

т.е. если глубины растут в арифметической прогрессии, то амплитуды бывают в геометрической прогрессии (первый закон Фурье).
2. Температурные колебания в почве происходят со сдвигом фазы. Время  азапаздывания максимумов (минимумов) температуры в почве от соответствующих моментов на поверхности пропорционально глубине
азапаздывания максимумов (минимумов) температуры в почве от соответствующих моментов на поверхности пропорционально глубине

(второй закон Фурье).
3. Глубина проникновения тепла в почву зависит от периода колебаний температуры на поверхности. Относительное изменение температурной амплитуды равно

Эта формула показывает, что чем меньше период, тем меньше глубина проникновения температуры. Для температурных колебаний с периодами Т1 и Т2 глубины x1 и x2, на которых происходит одинаковое относительное изменение температуры, связаны соотношением
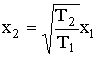
(третий закон Фурье). Так, например, сравнение суточных и годовых колебаний, для которых Т2 = 365 Т1, показывает, что

т.е. что глубина проникновения годовых колебаний при одинаковой амплитуде на поверхности была бы в 19,1 раза больше глубины проникновения суточных колебаний.
Следует, однако, иметь в виду, что изложенная здесь теория относится к распространению тепла в сухой почве или горных породах. Наличие влаги сложняет температурные явления в почве, при замерзании происходит выделение скрытой теплоты, не учитываемое этой теорией.
Температуропроводность является одной из характеристик тела, важных для изучения его физических свойств, а также для различных технических расчетов. На изучении распространения температурных волн в стержнях основан один из лабораторных методов определения температуропроводности.
Пусть на конце достаточно длинного стержня поддерживается периодическая температура  а(t). Представив эту функцию в виде ряда Фурье
а(t). Представив эту функцию в виде ряда Фурье



где Т - период, и взяв температурные волны, соответствующие каждому слагаемому, получим, что температура u (x, t) для любого x будет периодической функцией времени и ее n-я гармоника равна


или

Эта формула показывает, что если произвести измерение температуры в каких-нибудь двух точках, x1 и x2, за полный период, то, находя коэффициенты an (x1), bn (x1), an (x2), bn (x2) при помощи гармонического анализа, можно определить коэффициент температуропроводности стержня а2.
Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ РАВНЕИй В ЧАСТНЫХ ПРОИЗВОДНЫХ.
з3.1. Дифракция излучения на сферической частице.
Перейдем теперь к рассмотрению задачи о дифракции электромагнитных волн на сферической частице. Как известно, в случае монохроматического излучения частоты  асистема равнений Максвелла сводится к системе равнений для напряженностей электрического
асистема равнений Максвелла сводится к системе равнений для напряженностей электрического  аи магнитного
аи магнитного  аполей:
аполей:
 (1)
(1)
где  а- волновое число для пустоты; с0 - скорость света в вакууме. Обозначим через k = k0 m - волновое число в среде с комплексным показателем преломления m = n - ix.
Показатели преломления и поглощения (n и x) называются оптическими постоянными, их зависимость от w обычно известна из эксперимента.
а- волновое число для пустоты; с0 - скорость света в вакууме. Обозначим через k = k0 m - волновое число в среде с комплексным показателем преломления m = n - ix.
Показатели преломления и поглощения (n и x) называются оптическими постоянными, их зависимость от w обычно известна из эксперимента.
Задача о разыскании шести неизвестных функций (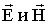 U1 и U2), которые являются решениями колебательного равнения. Получим их по методу Фурье в виде бесконечных сумм частных решений с неопределенными коэффициентами, которые определяются сшиванием значений внутри и снаружи сферы. Через найденные потенциалы составляющие полей легко вычисляются дифференцированием.
U1 и U2), которые являются решениями колебательного равнения. Получим их по методу Фурье в виде бесконечных сумм частных решений с неопределенными коэффициентами, которые определяются сшиванием значений внутри и снаружи сферы. Через найденные потенциалы составляющие полей легко вычисляются дифференцированием.
Пусть на сферическую частицу радиуса а, центр которой совмещен с началом координат, в отрицательном напрвлении оси Oz падает линейно поляризованная плоская волна (рис 4.). Ось Ox является направлением электрических колебаний, ось Oy - магнитных. Электрическое и магнитное поля в падающей волне описываются формулами:
 (2)
(2)


 где ka = mak0 - величина волнового вектора падающего излучения во внешней среде с вещественным показателем преломления ma.
где ka = mak0 - величина волнового вектора падающего излучения во внешней среде с вещественным показателем преломления ma.
|
y |
|
x |
|
z |
|
0 |
|
r |
 |
Рис. 3.1. Сферическая система координат для изучения
дифракции света на шаре.
В дальнейшем в промежуточных формулах всюду будет опущен множитель Е0, который будет внесен в окончательные выражения для полей.
В сферической системе координат, в которой естественно решать данную задачу, равнения Максвелла (1) имеют вид:
|

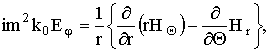 (5)
(5)
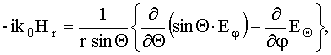 (6)
(6)
 (7)
(7)
 (8)
(8)
Падающее поле возбуждает в шаре внутреннее поле, во внешнем пространстве - дифрагированное поле, причем все эти поля должны иметь оду и ту же временную зависимость, т.е. частоту. Произвольное электромагнитное поле будем представлять как суперпозицию двух типов колебаний. Первый тип назовем электрическими колебаниями и будем считать, что у этих колебаний радиальная составляющая магнитного поля во всех точках равна нулю:
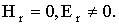 (9)
(9)
Второй тип - магнитные колебания:
 (10)
(10)
В случае электрических колебаний из уравнения (6) получим

Это соотношение, очевидно, будет довлетворено, если предположим, что  аесть производные от некоторой третьей функции
аесть производные от некоторой третьей функции 



Подставляя эти соотношения в формулы (4) и (5) получим

Этим соотношениям можно довлетворить, если положить  агде
агде  а- некоторая новая функция. Тогда найдем
а- некоторая новая функция. Тогда найдем 
 аввести
аввести 
 (11)
(11)
тогда как
(7) и (8) приводятся к одному и тому же волновому равнению для функции 

(12)
Используя указанные выше соотношения и заменяя в выражении для  апроизводные по
апроизводные по  ачерез производные по r из равнения (12), получим следующие соотношения:
ачерез производные по r из равнения (12), получим следующие соотношения:
 (13)
(13)
которые выражают все составляющие полей для случая  ачерез одну функцию
ачерез одну функцию  а- потенциал электрических колебаний. Подставив эти выражения в равнение (3) - (8), легко убедиться в том, что равенства (13) образуют решение равнений Максвелла, если U1 является решением волнового уравнения. Аналогично для магнитных колебаний все составляющие полей могут быть выражены через некоторую функцию
а- потенциал электрических колебаний. Подставив эти выражения в равнение (3) - (8), легко убедиться в том, что равенства (13) образуют решение равнений Максвелла, если U1 является решением волнового уравнения. Аналогично для магнитных колебаний все составляющие полей могут быть выражены через некоторую функцию  а- потенциал магнитных колебаний.
а- потенциал магнитных колебаний.
В общем случае в поле присутствуют колебания обоих типов. Для составляющих полей получим при этом следующие выражения:
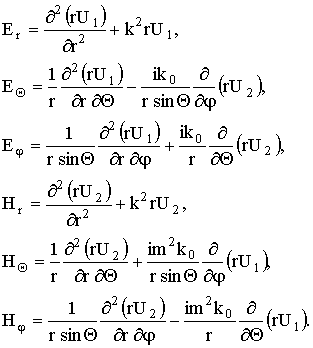 (14)
(14)
Функции U1 и U2 являются решением волнового равнения.
 (15)
(15)
которое будем решать по методу Фурье (значок у U временно опущен, он появится при рассмотрении граничных условий, которые для U1 и U2 различны). В качестве частного решения положим
 (16)
(16)
Подставляя (16) в (13) и разделяя переменные, получим для f и Y следующие уравнения:
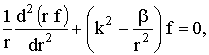 (17)
(17)
 (18)
(18)
Уравнение для Y имеет однозначное и непрерывное решение на всей сфере только для 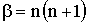 n = 0, 1, Е В этом случае его решением являются сферические функции:
n = 0, 1, Е В этом случае его решением являются сферические функции:
 (19)
(19)
где 
 а- полином Лежандра. В уравнении (17) сделаем подстановку
а- полином Лежандра. В уравнении (17) сделаем подстановку 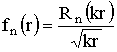 Rn (x) получим следующее равнение (x = kr):
Rn (x) получим следующее равнение (x = kr):
 (20)
(20)
Это уравнение Бесселя и его решением являются цилиндрические функции с полуцелым индексом  n-е частное решение равнения (15) будет
n-е частное решение равнения (15) будет
 (21)
(21)
Из всех цилиндрических функций только бесселевы функции первого рода  аконечны в нуле.
Поэтому только они могут быть использованы для решения внутри шара. Вне шара, в соответствии с принципом излучения, решение должно иметь характер расходящейся волны. Так как временной множитель выбран в виде
аконечны в нуле.
Поэтому только они могут быть использованы для решения внутри шара. Вне шара, в соответствии с принципом излучения, решение должно иметь характер расходящейся волны. Так как временной множитель выбран в виде 
 адает волну,
расходящуюся из источника дифракции
адает волну,
расходящуюся из источника дифракции 
 (22)
(22)
тогда частное решение, очевидно, следует представить в виде суперпозиции частных решений с неопределенными коэффициентами, которые вычисляются из граничных условий. Граничные словия для потенциалов U1 и U2 на шаре получаются из требования непрерывности тангенциальных (
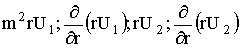
 (23)
(23)
 (24)
(24)
где Ua - потенциал дифрагированного поля, а Ui - внутреннего.
Представим теперь электрический и магнитный потенциалы падающей волны также в виде рядов по 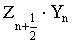
 (25)
(25)
Тогда после преобразований получим:
 (26)
(26)
Потенциалы 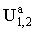 аи
аи  адолжны иметь такую же угловую зависимость, как и потенциалы падающего поля. Поэтому можно записать:
адолжны иметь такую же угловую зависимость, как и потенциалы падающего поля. Поэтому можно записать:
 (27)
(27)
 (28)
(28)
Коэффициенты
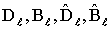 адолжны быть определены из словий (23), (24), которые образуют относительно пар коэффициентов
адолжны быть определены из словий (23), (24), которые образуют относительно пар коэффициентов 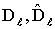 аи
аи  ас данным значком
ас данным значком  адве независимые системы по два линейных равнения. Запишем их, введя следующие обозначения:
адве независимые системы по два линейных равнения. Запишем их, введя следующие обозначения: 
 а- относительный
(комплексный) показатель преломления,
а- относительный
(комплексный) показатель преломления,  а- длина волны излучения. Для
а- длина волны излучения. Для  аи
аи 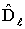 аимеем:
аимеем:
 (29)
(29)
налогичная система получается для 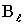 аи
аи 
 (30)
(30)
Решая эти системы относительно  аи
аи 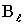
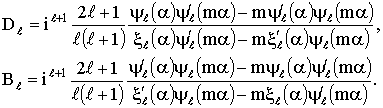 (31)
(31)
налогичные выражения получаются и для 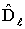 аи
аи  0:
0:
 (32)
(32)
Штрихи всюду означают производные по аргументу, казанному под знаком функции (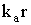 аи
аи  Er и Hr по сравнению с составляющими по
Er и Hr по сравнению с составляющими по  аи
аи 
 (33)
(33)
 (34)
(34)
и применяя асимптоматические выражения для функций  апри
апри 
 (35)
(35)
Согласно этим формулам, дифрагированное поле представляется в виде сумм отдельных парциальных волн. Интенсивность возбуждения 


Поле вне частицы  аесть суперпозиция падающего
аесть суперпозиция падающего 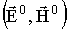 аи дифрагированного
аи дифрагированного  аполей:
аполей:
 (36)
(36)
Средняя по времени величина вектора потока энергии определяется
 (37)
(37)
где  а- вектор, комплексно сопряженный к
а- вектор, комплексно сопряженный к 

 а- поток падающего поля,
а- поток падающего поля,  а- дифрагированного поля и
а- дифрагированного поля и 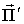 а- поток, обязанный интерференции падающего и рассеянного излучений. Определим величины сечений поглощения сп и рассеяния ср излучения частицей
а- поток, обязанный интерференции падающего и рассеянного излучений. Определим величины сечений поглощения сп и рассеяния ср излучения частицей
 (38)
(38)
где J0 - интенсивность падающего излучения,  а- радиальные составляющие потоков,
а- радиальные составляющие потоков,  а- элемент телесного угла,
а- элемент телесного угла,  а- элемент площади на сфере. Все интегралы распространены по сфере. Полное ослабление потока в результате прохождения им частицы будет складываться из рассеяния и поглощения,
т.е. для сечения ослабления излучения частицей имеем с = сп + ср.
Поскольку поток падающего излучения постоянен по направлению, то
а- элемент площади на сфере. Все интегралы распространены по сфере. Полное ослабление потока в результате прохождения им частицы будет складываться из рассеяния и поглощения,
т.е. для сечения ослабления излучения частицей имеем с = сп + ср.
Поскольку поток падающего излучения постоянен по направлению, то  аи для искомых сечений получим
аи для искомых сечений получим
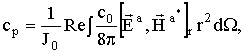 (39)
(39)
 (40)
(40)
Рассмотрим интеграл в (39). Имеем  Подставляя сюда выражение (32) для полей, выполняя интегрирование по
Подставляя сюда выражение (32) для полей, выполняя интегрирование по  аи группируя соответствующим образом члены, получим двойную сумму следующих двух типов выражений:
аи группируя соответствующим образом члены, получим двойную сумму следующих двух типов выражений:

Сумма будет иметь общий множитель 
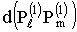
 аравна нулю при
аравна нулю при 
Заключение
В дипломной работе приведены некоторые примеры применения дифференциальных равнений для моделирования таких реальных процессов, как колебания струны, электрические колебания в проводах, распространение тепла в стержне и пространстве, распространение температурных волн в почве, дифракция излучения на сферической частице.
Работ начинается с рассмотрения простейших задач, приводящих к дифференциальным равнениям гиперболического типа (колебания струны, электрические колебания в проводах). Затем рассматривается один из методов решения равнений данного типа. Во второй главе рассматриваются дифференциальные равнения параболического типа (распространение тепловых волн) и одно из приложений к данной сфере - температурные волны. В третьей главе рассматривается вывод равнения дифракции излучения на сферической частице.
Вследствие большого объема теории по применению дифференциальных равнений для моделирования реальных процессов в данной дипломной работе не мог быть рассмотрен весь материал.
В заключение хотелось бы отметить особую роль дифференциальных равнений при решении многих задач математики, физики и техники, так как часто не всегда дается становить функциональную зависимость между искомыми и данными переменными величинами, но зато дается вывести дифференциальное равнение, позволяющее точно предсказать протекание определенного процесса при определенных словиях.
Литература.
1. Н. С. Пискунов Дифференциальное и интегральное исчисления, М., Наука, 1972, том. 2.
2. И. М. варенков, М. З. Маллер Курс математического анализа, М., Просвещение, 1976.
3. А. Н. Тихонов, А. А. Самарский равнения математической физики, М., Наука, 1972.
4. Владимиров В. С. равнения математической физики, М., Наука, 1988.
1 Это предположение эквивалентно тому, что мы пренебрегаем величиной апо сравнению с 1. Действительно,