Читайте данную работу прямо на сайте или скачайте
Диагностика математических понятий у учащихся
Содержание
Введение 5
1 Теоретико-методологические основы исследования 9
1.1 О подходах к введению математических поня тий 9
1.1.1 Конкретно-индуктивный и абстрактно-дедуктивный подходы 9
1.1.2 Дея тельностный подход 10
1.1.3 Исследовательский подход 12
1.1.4 Как быть с лнерабочими определения ми? 18
1.2 Роль дефиниций в математической дея тельности учащихся 20
1.2.1 Отыскание описательного определения , не расширя ющего объем
поня тия 20
1.2.2 Формулировка определения путем обобщающего описания 21
1.2.3 Формулировка определения посредством конструктивного описания 25
1.2.4 Формулировка определения , основанная на аналогии и переносе 27
1.2.5 Формулировка определений на основе классификации 28
1.2.6 Формулировка определения путем выделения частного случая 30
1.2.7 Формулировка определения посредством обобщения известного определения 31
1.3 Формирование математических поня тий у учащихся 32
2 Экспериментальные исследования диагностики математических
поня тий у учащихся 43
2.1 Значение вопроса при диагностике математических поня тий у учащихся на роках математики 43
2.2 К вопросу о диагностике математического поня тия "величина" 47 2.3 Диагностика ровня сформированности математических поня тий (метод ключевых поня тий) 56
2.4 Исследование процесса сравнения поня тий учащимися 11 класс 65
Заключение 67
Список используемых источников 69
Введение
Формирование научных понятий - одна из главных задач обучения математике в школе. Под математическим понятием будем подразумевать систему логически взаимосвязанных порядоченных суждений, высказанных о некотором математическом объекте. Эти суждения называются свойствами и признаками понятия и составляют его содержание. Формирование конкретного понятия тесно связано с своением чащимися соответствующего математического объекта и возникновением общего представления о нем. своить понятие - значит, своить систему знаний о некотором объекте и научиться использовать их в деятельности.
Но чаще всего ребята называют признаки и свойства математических понятий, которые были подробно рассмотрены в соответствующих пунктах учебника, т.е. являлись объектом специального изучения. Другие суждения о понятии (с которыми чащиеся знакомятся в процессе решения задач или при изучении других понятий), как правило, не включаются в его содержание и сваиваются как отдельные факты, вне связи с понятием. Кроме того, школьники не владеют приемами деятельности, позволяющими успешно рассуждать, решать задачи, т.е. применять понятие в деятельности.
Это связано с тем, что в школьной практике формирование понятии как целенаправленный процесс осуществляется слабо [6]. Анализ конспектов роков чителей показал, что формирование понятия как цель урока чителями даже не ставится (цели более зкие: изучить теорему, научить решать некоторые виды задач и др.), роки обобщения и систематизации знаний, на которых должны обобщаться и логически порядочиваться знания о формируемых понятиях, чаще всего превращаются в роки повторения по данной теме. Это (и многое другое) ведет к фрагментарности знаний, неумению применять их на практике.
Одной из причин такого положения является сложившееся и укоренившееся в методике обучения математике за последние десятилетия неверное представление о понятии и его формировании, при котором математический объект и математическое понятие не различались, формирование понятия связывалось с его определением [6].
Поэтому при изучении основных понятий курса математики в средней школе необходимо своевременно устанавливать, преобразуется ли сообщаемая чащимся информация в знания, основанные на долговременном запоминании, не оперативном, как это часто бывает. Это важно потому, что в школе закладывается основной понятийный аппарат, на базе которого впоследствии будут строиться более сложные математические теории.
Исходя из этого перед учителем математики стоят две задачи.
Первая - правильно формировать математические понятия.
Вторая - делать экспертную оценку сформированности понятийного аппарата изученных тем.
Первой задаче соответствует традиционно применяемые на роках различные подходы к введению и формированию математических понятий [6]. Дидактический материал, предлагаемый для этого, обширен и разнообразен [28]. Для второй задачи нет четко определенных и отработанных методов. Отчасти она решается на роке стным опросом при повторении пройденных тем. Но, очевидно, этот метод не позволяет охватить всех учащихся класса и является лишь эпизодическим. Поэтому организация диагностики математических понятий у учащихся является актуальной, что и послужило причиной выбора этой темы в качестве выпускной работы.
Объект исследования - математические понятия.
Предмет исследования - диагностика математических понятий у учащихся.
Цель исследования - найти методы диагностики сформированности понятийного аппарата, показать их эффективность в процессе обучения математике.
Для достижения поставленной цели необходимо решить следующие задачи:
1) пронализировать психолого-педагогическую и методическую литературу, посвящённую проблеме диагностики математических понятий у учащихся и найти методы диагностики сформированности понятийного аппарата;
2) рассмотреть основные подходы к введению математических понятий;
3) раскрыть роль определений в математической деятельности учащихся;
4) показать, как конструинруется собственно методическая концепция формиронвания математических понятий;
5) показать значение вопросов при диагностике математических понятий у учащихся на роках математики;
6) выявить уровень сформированности понятия "величина" у учащихся класса
7) рассмотреть метод ключевых понятий, который хонрошо отвечает задаче оценки сформированности понятийного апнпарата;
8) выявить, как изменяется определение понятий в процессе их своения на примере чеников XI класса;
9) пронализировать результаты экспериментальных исследований.
Работа состоит из введения, двух разделов, заключения и списка использованных источников.
В первом разделе " Теоретико-методологические основы исследования " рассматриваются различные подходы к введению математических понятий: конкретно-индуктивный, абстрактно-дедуктивный, деятельностный и исследовательский подходы; раскрывается роль дефиниций в математической деятельности учащихся, также показывается, как конструируется собственно методическая концепция формирования математических понятий, описываются методические требования к формированию понятий.
Практическая часть представлена во второй главе работы "Экспериментальные исследования диагностики математических понятий у учащихся". Здесь показано значение вопроса при диагностике математических понятий у учащихся на роках математики и представлены различные методики с целью определения сформированности математических понятий в соответствии с нормативными характеристиками в различных классах.
В результате теоретического и экспериментального исследования становлено, что очень важно при изучении основных поня тий своевременно станавливать, преобразуется ли сообщаемая чащимся информация в знания , основанные на долговременном запоминании, не оперативном, так как в школе закладывается основной поня тийный аппарат. При этом, я думаю, существенную роль играет то, как читель смог сформировать то или иное поня тие. Но не каждое поня тие нужно вводить основательно, так как некоторые поня тия (предел, непрерывность и предел функции) сложны и плохо сваиваются чащимися . Лучше высвободившееся время делить формированию общего представления о новых математических поня тия х, основывая сь на знании их геометрического и физического смысла (в случае производной) или на нагля дных представления х учащихся (в случае предела и непрерывности функции). Это будет честнее, чем требовать от чеников запоминания недоступных их пониманию определений, которые в дальнейшем все равно не применя ются .
1 Теоретико-методологические основы исследования
1.1 О подходах к введению математических поня тий
1.1.1 Конкретно-индуктивный и абстрактно-дедуктивный подходы
В методике под введением математического поня тия подразумевают этап ознакомнления учащихся с новым математическим объектом, заканчивающийся его определением. В специальной литературе до недавнего времени рассматривались два подхода к введению математических поня тии: конкретно-индуктивный (переход от частного к общему, от примеров - к определению) и абстрактно-дедуктивный (переход от общего к частному, от определения - к примерам) [6].
Основное достоинство первого подхода заключается в том, что при введении нового поня тия читель опирается на знания и жизненный опыт учащихся , что само по себе предполагает их активное частие в работе. Этот подход способствует развитию индуктивного мышления школьников.
В методической практике сложилось неверное представление о том, что определение можно лоткрыть. По этому поводу Г.Фрейденталь писал: Как можно определить нечто, коль скоро не знают, что определя ют? [33]. А.С. Мищенко заметил, что внешне дея тельность лпо открытию определения на роке выгля дит вполне современно, побуждает чеников к анализу ситуации, как говоря т лактуализирует их мыслительную дея тельность. В действительности, казанный способ введения поня тия утомля ет детей и создает неверное представление о науке математике в целом. Все силия на этом этапе должны быть направлены на закрепление потребления поня тий (соответствующих терминов, обозначений) и их свойств в строгих математических формулировках для того, чтобы опираться на них в процессе математических рассуждений [18]. Основная роль определений в математике - служить начальным звеном в дедуктивном поря дочении суждений о некотором поня тии.
бстрактно-дедуктивный подход обычно используется , когда определение нового объекта не сложно по структуре, сам объект знаком ченикам. В этом случае его существенные свойства легко обнаруживаются у объектов, рассматриваемых в качестве примеров. Этот подход более экономичен по времени, но после введения нового определения со сложной структурой требуется некоторая (нередко значительная ) работа по его своению. Так, часть определений курса геометрии и математического анализа школьники сваивают только после целенаправленной работы, основанной на изучении их структуры [20].
Например, распознавание пря мой, перпендикуля рной плоскости, несложно. У учащихся есть представления о предметах, расположенных вертикально относительно поверхности земли. Затруднения школьников при изучении данной темы свя заны, прежде всего, с изображением пространственных объектов на плоскости и сложностью структуры самого определения , формулировка которого содержит слово любой: пря мая называется перпендикуля рной плоскости, если она перпендикуля рна любой пря мой, лежащей в плоскости. Отметим, что абстрактно-дедуктивный подход можно применить при введении любого поня тия . Приня то считать, что он развивает теоретическое мышление школьников.
Оба рассмотренных подхода основаны на абстракции отождествления Цпроцессе отвлечения от исходных, различающихся свойств предметов и выделении их одинаковых, тождественных свойств. Эти подходы в достаточной степени обеспечивают реализацию ориентировочной функции поня тия , позволя ющей веренно подводить под поня тия конкретные объекты.
1.1.2 Дея тельностный подход
Сущность данного подхода заключается в том, что, взя в за основу некоторое свойство (или несколько свойств) математического объекта в качестве основания классификации, чащиеся под руководством чителя проводя т классификацию математических объектов по этому основанию [6]. В результате такой работы одному из получившихся классов присваивается некоторое название и дается определение объектов данного класса, т.е. начинается формирование нового поня тия [10], [22].
Рассмотрим применение дея тельностного подхода при введении поня тий параллелограмм и трапеция .
Учитель. Из каких элементов состоит четырехугольник?
Ученик. Из сторон и глов.
Учитель. Какие отношения можно рассматривать для отрезков - сторон четырехугольника?
Ученик. Отношения равенства, параллельности, перпендикуля рности.
Учитель. Наша задача - изучить четырехугольники с точки зрения наличия у них параллельных сторон. Существует ли четырехугольник с одной парой параллельных сторон?
Ученик. Да.
Учитель. Как это доказать?
Ученик. С помощью построения такого четырехугольника.
(Один из чеников строит фигуру на доске, остальные - в тетрадя х.)
Учитель. Существует ли четырехугольник с двумя парами параллельных сторон?
Ученик. Да.
(Делаются соответствующие построения .)
Учитель. Можно ли построить четырехугольник с тремя и более парами параллельных сторон?
Ученик. Нет.
Учитель. Почему?
Ученик, Смежные стороны имеют общую точку, поэтому параллельными могут быть только противоположные стороны. А их две пары.
Учитель. Существует ли четырехугольник, у которого нет параллельных сторон?
Ученик. Существует.
(Выполня ются построения на доске и в тетрадя х.)
Таким образом, всего получилось три различных вида четырехугольника: с одной парой параллельных сторон - трапеция , с двумя - параллелограмм, и четырехугольник, не имеющий ни одной пары параллельных сторон, у него нет специального названия .
Далее читель вводит термины параллелограмм и трапеция , рассказывает о том, что эти четырехугольники изучались с древности. Они имеют много интересных и полезных с практической точки зрения свойств, поэтому для дальнейшей работы нужно ввести их строгие определения . Учащиеся без труда отвечают на вопрос, какой четырехугольник называется параллелограммом, поскольку знают основание классификации. Затем формулируется определение трапеции. После этого начинается изучение свойств и признаков введенных поня тий [6].
Дея тельностный подход способствует пониманию чащимися метода научного познания действительности, чит основам классификации. Он предполагает активное частие школьников в познавательной дея тельности. С другой стороны, этот метод требует немалых затрат времени. Кроме того, он дает хороший результат лишь там, где классификация объектов по определя ющему признаку возможна и целесообразна [13]. Так, дея тельностный подход местен, когда вводится отношение между объектами, например, при изучении гла, вписанного в окружность; взаимного расположения пря мой и окружности, двух плоскостей и т.д.
1.1.3 Исследовательский подход
Если рассмотренные выше подходы позволя ют лишь ввести новое поня тие, то исследовательский подход направлен на его формирование в целом (как системы взаимосвя занных логически поря доченных суждений). При этом можно организовать познавательную дея тельность учащихся таким образом, чтобы воспроизвести (с некоторой долей достоверности!) дея тельность ченого-математика, направленную на изучение нового объекта и образование поня тия [6]. Напомним, что при исследовательском подходе совместная дея тельность учителя и учащихся включает следующие этапы:
- постановка цели дея тельности;
- эмпирическое изучение нового математического объекта, поиск его свойств;
- формулирование найденных свойств в виде гипотез;
- введение нового термина, определение математического объекта;
- проверка истинности высказанных предположений путем отыскания их доказательств;
- поиск признаков исследуемого объекта (рассмотрение обратных тверждений);
- точнение логических свя зей между суждения ми, схематизация содержания нового поня тия ; своение этого содержания ;
- обучение применению нового поня тия в дея тельности: решение опорных задач, выделение общих приемов дея тельности, способствующих применению поня тия (например, отыскание эвристик);
- применение поня тия в нестандартных ситуация х [26].
Покажем, как может осуществля ться исследовательский подход при изучении поня тия лравнобедренная трапеция .
Традиционно это поня тие вводится в теме Трапеция . Но его подробное рассмотрение можно отложить до момента, когда будет изучаться теорема Пифагора, поскольку именно в последней теме поня тие трапеции широко применя ется при решении задач [6].
Класс разбивается на группы. Перед началом беседы учитель раздает ченикам (каждому или по одному на группу) чертежи равнобедренной трапеции.
Учитель. Назовите основные элементы трапеции.
Ученик. Стороны, глы, диагонали.
Учитель. Сегодня на роке мы попробуем изучить данный четырехугольник, как, возможно, много веков назад это сделали ченые-математики. Вспомните, что интересует геометров при изучении фигур в первую очередь?
Ученик. Соотношения между ее сторонами и глами.
Учитель. Так кто же сформулирует цель нашего исследования ?
Ученик. Цель Ч выя вить соотношения между элементами трапеции, т.е. между сторонами и глами. А также изучить другие особенности фигуры.
Учитель. Математики же в древности знали немало свойств и признаков этого четырехугольника. Возьмите в руки линейки, транспортиры. Измерьте, а затем сравните стороны, глы трапеции, ее диагонали. Сформулируйте гипотезы о свойствах этих элементов трапеции.
После работы в группах беседа возобновля ется .
Учитель. Каким свойством обладают боковые стороны трапеции?
Ученик. Они равны.
Учитель. Каким свойством обладают углы этой трапеции?
Ученик. глы при каждом основании трапеции равны. читель. Каким свойством обладают диагонали трапеции?
Ученик. Они равны.
Учитель. Какие еще особенности этой трапеции вы заметили?
Ребя та могут добавить, например, такие суждения :
- высоты трапеции, проведенные из вершин меньшего основания , отсекают от нее равные пря моугольные треугольники;
- диагонали разбивают трапецию на два равных и два равнобедренных треугольника.
Если ченики называют свойства, которыми обладает любая , не только равнобедренная , трапеция , то читель дает соответствующие поя снения и не включает эти свойства в список [6]. Беседа возобновля ется .
Учитель. Можно ли считать, что мы с вами изучили данную фигуру?
Ученик. Нет. Пока у нас есть только гипотезы.
Учитель. Что же нужно сделать дальше?
Ученик. Надо их доказать.
Учитель. Но ученые доказывают теоремы. Сформулируйте хотя бы одну из них.
Поскольку чащиеся не могут использовать термин лравнобедренная трапеция (который еще не введен), они предлагают суждения типа: Если боковые стороны трапеции равны, то ее глы при основания х также равны, Если боковые стороны трапеции равны, то ее диагонали равны и т.д. читель должен обратить внимание школьников на большое количество тверждений и на тот факт, что одни из них следуют из других [35]. Например, при словии, что окажутся верными тверждения : если боковые стороны трапеции равны, то и глы при основании равны и если глы при основании трапеции равны, то ее диагонали равны, будет верно тверждение: если боковые стороны трапеции равны, то ее диагонали равны.
Далее дается определение равнобедренной трапеции, а гипотезы оформля ются в виде схемы (рисунок 1.1).

 Трапеция с равными боковыми сторонами
Трапеция с равными боковыми сторонами
 |
глы при Диагонали Другие
основании равны равны отмеченные свойства
Рисунок 1.1 Ца Гипотезы о свойстваха трапеции с равными боковыми сторонами
После этого каждая группа получает задание: сформулировать и доказать одну из теорем о свойствах равнобедренной трапеции, также обратную ей теорему. (Заметим, что в данном случае все приведенные выше тверждения и обратные к ним я вля ются истинными.) Можно дать это задание на дом (причем свойства, рассмотренные в учебнике, чащиеся должны попробовать доказать другим способом), тогда оно проверя ется на следующем роке. Очевидно, что не все ченики смогут его выполнить, в некоторых случая х задание может оказаться непосильным на данном этапе изучения . Отметим, что в процессе решения задач, также при изучении других тем, начатая работа может быть продолжена [6].
На следующем этапе у учащихся формируется мение применя ть поня тие лравнобедренная трапеция в речи, в рассуждения х при решении задач. Школьники должны научиться проговаривать импликативные высказывания в общеутвердительной, более соответствующей естественному я зыку, форме. Например, формулировку теоремы: если трапеция равнобедренная , то ее глы при основании равны, им следует произносить так: в равнобедренной трапеции глы при основания х равны. Кроме того, чащиеся должны уметь правильно перечисля ть свойства равнобедренной трапеции.
Обучение применению поня тия можно начать с рассмотрения опорных задач по данной теме, решение которых приводит к общим приемам дея тельности. Например, к приемам, способствующим применению поня тия лравнобедренная трапеция можно отнести следующие [11]:
- проведение высот из вершин меньшего основания (при этом образуются два равных пря моугольных треугольника и пря моугольник, рисунок 1.2);

Рисунок 1.2
- проведение из вершины меньшего основания отрезка, параллельного боковой стороне (трапеция разбивается на параллелограмм и равнобедренный треугольник, рисунок 1.3);

Рисунок 1.3
- проведение из вершины меньшего основания отрезка, параллельного диагонали трапеции (при этом образуется равнобедренный треугольник, равновеликий трапеции, рисунок 1.4).

Рисунок 1.4
Для актуализации каждого из приемов необходимо подобрать соответствующую задачу, решение которой не было бы громоздким.
В систему пражнений полезно также включить задачи, при решении которых требуется доказать, что трапеция я вля ется равнобедренной, т.е. на использование различных признаков поня тия [17]. При этом необходимо чить школьников правильно отвечать на вопрос: по каким признакам можно распознать равнобедренную трапецию среди других четырехугольников? (Например, по равенству диагоналей, глов при основании и др.)
Естественно, формирование поня тия лравнобедренная трапеция будет продолжаться и в дальнейшем. Его содержание будет пополня ться новыми признаками и свойствами:
- равнобедренная трапеция имеет одну ось симметрии;
- равнобедренную трапецию можно вписать в окружность;
- при пересечении диагоналей равнобедренной трапеции получаются два подобных равнобедренных треугольника и др.
Покажем, как можно применить исследовательский подход к формированию поня тия лквадратичная функция [6]. В средней школе основное внимание деля ется построению и чтению графика квадратичной функции. Решение же более сложных задач (к примеру, задач ЕГЭ с параметрами) требует от учащихся владения достаточно широким спектром ее свойств. В частности, знания того, как влия ют коэффициенты, входя щие в формулу квадратичной функции, на расположение ее графика относительно системы координат [11].
Исследование с целью отыскать такого рода зависимости можно провести в форме самостоя тельной групповой работы.
После выполнения работы подводя тся итоги. чащиеся сообщают результаты своих исследованний и с помощью чителя делают обобщения .
1.1.4 Как быть с лнерабочими определения ми?
Из вышесказанного вовсе не следует, что каждое поня тие нужно вводить так основательно. В школьном курсе математики имеются поня тия , которые традиционно привлекают внимание методистов. В частности, речь идет о таких поня тия х математического анализа, как предел, непрерывность функции и производная , определения которых сложны и плохо сваиваются чащимися [6]. ченики не только не понимают, но и не могут воспроизвести их по памя ти. При этом они достаточно спешно используют свойства этих поня тий в своей математической дея тельности.
Иногда у учащихся формируется неверное представление об изучаемых поня тия х, они путают их определения со свойствами. Так, в книге Б. Ц. Бадмаева приводится пример с определением смежных глов [1]. Как показал проведенный автором эксперимент, никто из учащихся не смог воспроизвести его правильно. Все они считали, что смежные глы - это глы, сумма которых равна 180
Можно привести еще немало примеров, когда ченики, не зная определения поня тия , умеют применя ть последнее в дея тельности. Это касается таких поня тий геометрии, как многогранник, цилиндр, конус и др. А в алгебре поня тие число, с которым ребя та работают ежедневно, вообще не определено. И это никого не смущает. Дело в том, что определения этих поня тий нерабочие, поскольку не применя ются в рассуждения х, при решении задач и нужны лишь для построения теории поня тия , т.е. для логического поря дочения суждений о нем. чащиеся же спешно работают с поня тием, основывая сь на нагля дном образе соответствующего объекта, созданном порою задолго до того, как поня тие начали изучать в школе.
Определения предела и непрерывности функции на промежутке плохо сваиваются учащимися не только потому, что сложны по структуре. Исследования показывают, что поня тие непрерывности функции на промежутке в сознании школьников опирается на нагля дные представления о поведении графика функции, соответствующее определение на практике не работает: все свойства непрерывных функций в дальнейшем разъя сня ются без опоры на него [20].
Определение производной в школе также я вля ется нерабочим. Время , затраченное чителем на разучивание алгоритма его применения к выводу некоторых формул дифференцирования , проходит для большинства учащихся впустую, такая работа не способствует даже запоминанию формул. На наш взгля д, в школе помя нутые выше поня тия матенматического анализа можно ввести без строгих определений. А высвободившееся время лучше делить формированию общего представления о новых математических поня тия х, основывая сь на знании их геометрического и физического смысла (в случае производной) или на нагля дных представления х учащихся (в случае предела и непрерывности функции). Это будет честнее, чем требовать от чеников запоминания недоступных их пониманию определений, которые в дальнейшем все равно не применя ются [6].
В классах с глубленным изучением математики и на факультативных заня тия х в общеобразовательной школе можно строить и теорию пределов, и теорию производной. Но даже в этом случае не стоит много времени деля ть изучению определений (по той же причине).
В математических классах необходимо рассказывать о роли определения в построении теории поня тия , в тех случая х, когда возможно, привлекать учащихся к построению теории поня тия на основе другого его определения [17].
Со способными ребя тами из обычных классов такую работу полезно проводить на заня тия х кружка. И делать это лучше на геометрическом материале, поскольку в геометрии теории поня тий выстроены аксиоматически. Так, после изучения поня тия лравнобедренная трапеция можно предложить чащимся самостоя тельно разработать его теорию, взя в за основу, например, следующее определение: трапеция называется равнобедренной, если ее диагонали равны. Подобная ранбота полезна как в методологическом плане, так и с точки зрения развития предметных мений школьников.
Итак, подчеркнем, что правильное ввендение математических поня тий, формирование каждого из них как системы взаимосвя занных упоря доченных суждений, разумное сочетание логического и содержательного аспектов в процессе изучения поня тий, - все это способствует их спешнному своению и применению в практической деня тельности.
1.2 Роль дефиниций в математической дея тельности учащихся
1.2.1 Отыскание описательного определения , не расширя ющего объем поня тия
На нагля дном уровне поня тие пря моугольника хороншо известно 12-летним ученикам. Они встречались с ним же в начальных классах. Само слово пря моугольник, обороты речи типа форма пря моугольника они слышат и потребля ют в повседневном общении. На роке, который описан у С. Крыговской [14], читель стремился упоря дочить знания чеников о пря моугольниках (поння тие параллелограмма им было уже известно). Он спросил: Какую геометрическую фигуру вы назовете пря моугольником? Из известных ченикам свойств пря моугольников они пытались отобрать те, которые, по их мнению, характеризуют пря моугольники наибонлее естественным образом. Среди ответов содержались следующие: Пря моугольник - это четырехугольник, л...это параллелограмм, л..это четырехугольник, имеюнщий пря мые углы (или пря мые глы и равные пронтивоположные стороны, пря мые углы и равные диагоннали). Ответы учеников - исходный материал для обнсуждения , направля емого чителем в нужное русло.
Во время обсуждения выя снилось, достаточно ли свендений в каждом ответе, чтобы иметь полное представнление о пря моугольнике, надо ли включать в опреденление все данные, считают ли чащиеся пря моугольнинком такой объект, как квадрат. Возникла возможность изменить ошибочные мнения , провести обоснования . При этом ченики овладевали полезными приемами анализа данных, подведения итогов, выделения словии и т. п.
Но нахождение определений в процессе беседы и точнения позиции не расширя ет области известных ченикам математических объектов [20]. Дея тельность учинтеля и учащихся выступает здесь как средство поря ндочения некоторых фактов, развития математической речи, анализа ситуаций. Применя ть этот прием введенния определения , разумеется , можно лишь в случае, если ченики активно частвуют в обсуждении, и при словии, что такой процесс вызывает живой интерес класса, как это было на роке, где проводилось опинсанное выше обсуждение. ченики спорили, сравнивали ответы, приводили контрпримеры, сопровождали их ринсунками на доске.
1.2.2 Формулировка определения путем обобщающего описания
Расширение известного ченикам круга математиченских поня тий в ря де случаев можно свя зать с нахожндением определения путем обобщающего описания . Приведем несколько примеров [14].
) На пя том году обучения ченики знакомя тся с поння тием выпуклой фигуры. В одном из классов это бынло организовано так. Рассматривались контурные карнты нескольких вымышленных стран. Ученики отвечали на вопросы: Всегда ль можно соединить две точки страны на карте пря мым путем, не пересекающим гранницу? По этому признаку ченики разделили страны на два типа: безопасные и опасные. Жители безопаснной страны могут, не покидая ее, добраться по пря мой из любой точки страны в любую другую; для опасной страны такого пути может не быть. Учитель ввел тернмин выпуклая фигура для изображений безопасных стран. После небольшого числа упражнений ченики научились различать выпуклые и невыпуклые фигуры.
Теперь ребя т попросили написать письмо другу - ченнику того же класса (ученики обмениваются письмами попарно) и рассказать в нем, как надо понимать выранжение выпуклая фигура. Оказалось, что текст своего письма многим пришлось дополня ть стным разъя сненнием. Ребя та были довольно критически настроены по отношению к чужим формулировкам, так что возникшее обсуждение получилось живым иа поучительным.
анализ формулировок привел к интересным заключенния м. В письмах сказались разные ровни владения вынразительными средствами я зыка, которые выделил Г. Фрейденталь [33]. Например, встречался ля зык рисуннков: в качестве объя снения ченик поместил рисунки выпуклых и невыпуклых фигур. Поя вля лись и не всегнда дачные попытки использовать ля зык структур отнношений. В данном случае это выражалось в том, что рисунок выпуклом или невыпуклой фигуры дополня лся изображения ми отрезков, соединя ющих некоторые точки этих фигур.
Попадались и правильно построенные опинсания , например: Из одной точки фигуры в другую всегда можно провести отрезок, содержащийся в выпукнлой фигуре. В невыпуклой фигуре бывает, что это ненвозможно. Видно, что в этом ответе отражен опыт путешествий по вымышленным странам. Отметим такнже использование кванторова лвсегда, бывает.
Нет нужды на данном ровне освоения поня тия стренмиться к полной формализации. Здесь самое важное - переход от рассмотрения исходного сюжета к матемантическим представления м. Введение формального опренделения , его своение, расширение и точнение объема введенного поня тия можно провести только в дальнейншей беседе и при умелом руководстве ею. Допустим, читель спрашивает: Выпуклая ли фигура отрезок? Некоторые ченики отвечают отрицательно: Отрезок не выпуклый, он пря мой. Тогда читель задает второй вопрос: Можно ли каждую его точку соединить с люнбой другой отрезком, целиком в нем содержащимся ? Ответ, конечно, твердителен. Значит... - читель денлает многозначительную паузу, подготавливая учеников к парадоксальному для них выводу,Ч отрезок тоже вынпуклая фигура. В такой беседе читель нацеливает ренбя т на формальный путь применения ими же предложеых определений. Это пока что еще очень осторожный шаг вперед в направлении осознания роли определений в математике [34].
б) С периодическими функция ми 14-летние ученики еще не встречались. На одном из роков читель решил дать им представление о таких функция х до системантического изучения тригонометрии, так как ребя т обычно отождествля ют класс периодических функций с классом функций тригонометрических.
Учитель поставил задачу построить схематически гранфики функций:
1) 
2) 
3) 
После построений ребя та заметили, что графики именют общую важную особенность. Один из чеников дал ее интересное описание:
можно сделать шаблон части графика; в первом случае длина шаблона равна 1, во втором - 2, в третьем - 6; если передвигать его вдоль оси абсцисс, то можно изобразить весь график. Для функции 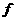 адостаточно перемещать шаблон на 1 в обоних направления х,
для
адостаточно перемещать шаблон на 1 в обоних направления х,
для  а- на 2 в обоих направления х, для
а- на 2 в обоих направления х, для  а- на 6 в положительнома направлении.
а- на 6 в положительнома направлении.
Учитель попросил описать выделенное свойство, пользуя сь не геометрическими, арифметическими поння тия ми, т. е. как свойство функций, не их графинков. Затем он сообщил, что рассматриваемое свойстнво называется периодичностью, и попросил дать опренделение периодической функции (в классе речь шла только о периодических числовых функция х). Так математический мир ченика обогатился новыми объекнтами [14].
Работа над определением на данном этапе не может считаться законченной. Следует брать несущественные признаки, свя занные с конкретными примерами, раснсмотреть контрпримеры, поработать над текстом. Осонбое внимание надо обратить на то, чтобы основанием для полведения итогов служила формулировка определенния , данная самими чениками, формулировка, вырабонтанная в ходе обсуждения , постоя нных точнений и иснправлений. Еще раз подчеркнем важный момент ананлизируемого подхода: ученики в качестве данных именли геометрические объекты (графики функции), опинсание требовалось получить на ином я зыке - арифментическом. Замена я зыка я вля ется здесь некоторым эленментом формализации, доступным для 14-летних чеников [23].
Обратим внимание на один общий вопрос. В описываемых примерах учитель не шел по пути непосредстнвенного предъя вления четкого, окончательного текста. Напротив, несмотря на заведомые трудности, он искал подходя щие дидактические приемы, направленные на конструирование учениками собственного опреденления , ибо оно и сваивается , и запоминается легче. Такими приемами служили: разложение сложных преднставлений на отдельные простые ситуации, побужденние учеников к активному анализу конкретных образнных ситуаций в сочетании с последующим примененинем к ним же известного математического аппарата. Использовались также идеализация , экстраполя ция , преобразование определения к виду цепочки шагов, обнлегчающих его применение и своение.
Такой способ обучения целесообнразно применя ть на любом ровне, если есть необхондимость в точнении научного поня тия [25]. Нам не раз приходилось наблюдать такой момент: ченик, харакнтеризуемый как неспособный, который и сам признанвал себя таким, при работе над определением смог преодолеть весьма существенный барьер в формиронвании математического мышления . При этом процесс был настолько естественным, что ченик барьера не заметил и оперировала обобщенными математическими поня тия ми так же свободно, как в начальной школе он чился правильно жестикулировать, рисовать и чинтать.
1.2.3 Формулировка определения посредством конструктивного описания
Этот способ введения поня тия содержит две ханрактерные черты [14]:
1) исходным пунктом служат нечетнкие очертания , первая идея об объекте, который в дальнейшем станет предметом определения ; формулинровка определения я вля ется не столько описанном чего-то готового, сколько очередной модификацией объекта, возникающего на глазах;
2) человек, дающий опренделение, обладает некоторой свободой в предъя влении отдельных частей всей конструкции.
При простом описании ченик выбирает одно из известных ему свойств определя емого объекта и считанет его словием в дефиниции. При обобщенном описании это словие проя вля ется в предлагаемых к рассмотрению примерах, а затем оно используется как общее условие в дефиниции. В аконструктивном же описании словие в дефиниции дается самим ченником.
Приведем пример этого процесса, который набнлюдали в классе 14-летних чеников [16]. читель задал вопрос: На плоскости даны точка и множество. Что следует понимать под расстоя нием от данной точки до данного множества? ченики спорили, делали рисуннки, предлагая разные подходы. Все они стремились к тому, чтобы описать самый короткий путь от точки до фигуры. Наконец один из чеников представил синтуацию следующим образом: Имеется круг с центнром в данной точке. Круг растет, как мыльный пузырь, расширя ется и расширя ется , пока не коснется множенства. Радиус этого круга и есть расстоя ние от его центра до данного множества. В этот момент вмешалнся учитель и предложил применить это определение к различным случая м:
) фигура представля ет собой внутренность некоторого круга, точка находится вне этого круга;
б) фигура произвольна, точка принаднлежит этой фигуре;
в) фигура - внутренность какого-то квадрата, а точка выбрана на контуре квадрата.
Сопонставление привело чеников к последовательным точннения м, совершенствованию текста определения . В конце концов, предложена дефиниция : Пусть существунет круг с центром в данной точке и не содержащий внутри себя точек данного множества. Тогда расстоя нние от данной точки до данного множества - радиус самого большого такого круга. Если же такого круга не существует, то расстоя ние от точки до фигуры равнно нулю.
Конечно, это еще не очень удачное определение. Но на данном этапе обучения , когда ченики не знают поня тия границы числового множества, стиль препондавания геометрии навя зывает им определенные обранзы в качестве исходных, эта их дефиниция может счинтаться не только формально верной, но и адекватной тому, что желали назвать расстоя нием от точки до множества. (Заметим, что приведенное определение по отношению к плоскости эквивалентно определению, осннованному на поня тии нижней грани числового множенства) [14]. Для чеников было очевидно существование санмого большого круга, не содержащего внутри себя точек множества, для случая , когда данное множество непусто, центр круга не принадлежит ни данному множеству, ни его краю (т. е. замыканию).
Представленная ситуация отличается от предыдущих степенью свободы чеников в их высказывания х о предмете изучения , в изменении точек зрения , в ходе которого проигрывались различные определения , пронисходило уточнение интуиции, свя занной очень общим пониманием расстоя ния как меры самого короткого пути.
1.2.4 Формулировка определения , основанная на аналогии и переносе
Разнообразные проя вления инициативы чеников в обсуждении определений можно наблюдать при перенходе от планиметрии к стереометрии. Применя я к изнвестным плоским объектам (фигурам и преобразованния м) лоперацию величения размерности, чащиеся конструируют их пространственные аналоги.
Приходилось наблюдать, как 17-летние ученики самостоя тельно разрабатывали поня тия , доказывали теоремы, относя щиеся к трехмерной мере Жордана, опирая сь на аналогию с известной им плоской теорией меры (размерность поднимается путем замены квадрантов на кубы) [14]. Также самостоя тельно ченики определя нли ря д топологических поня тий (окрестность точки, внутренность множества, область), заменя я круг шанром, окружность сферой.
Но и ченики младше 17 лет при изучении локально-дедуктивного курса геометрии также могли произвондить подобный перенос. Например, в ходе беседы они смогли преобразовать определение параллельных пря мых (на плоскости) танким образом, что оно стало отвечать их представлению о параллельности в пространстве. В ходе такой беседы школьники определили перпендикуля рность пря мой и плоскости, перпендикуля рность плоскостей. Такая дея нтельность имеет большую общеобразовательную цеость. Ученики начинают понимать, что некоторые опнределения можно без изменений перенести из планиметнрии в стереометрию (отрезок, луч). Они видя т также, что при переходе из плоскости в пространство некотонрые определения нужно дополнить словием лежать в плоскости (окружность, шестиугольник). Но есть и такие определения , которые, будучи перенесенными в пространство без изменений, приводя т к более общим поня тия ма (ломаная ) [3].
В некоторых случая х возможны различные способы переноса. Демонстрация этих случаев приводит ченинков к мысли об условном характере определений. Нанпример, если считать тетраэдр аналогом треугольника и подня ть по размерности медиану грани тетраэднра, то получится сечение тетраэдра плоскостью, прохондя щей через медиану грани и противоположную вершинну. ченики, однако, не решаются на эту операцию, хотя легко соглашаются с тем, чтобы назвать медианой тетраэдра отрезок, концы которого - вершина тетранэдра и центр тя жести противоположной грани. Тогда из теоремы о делении медиан треугольника точкой их пересечения , поднимая размерность получаем ананлог - теорему о делении медиан тетраэдра точкой их пересечения в отношении 1:3. Высказанную гипотезу следует подтвердить доказательством.
Учитель должен ограничить свое частие в такого рода рассуждения х. Ему необходимо следить лишь за тем, чтобы беседа имела деловой характер, отсекать несерьезные и бессмысленные высказывания . Особую роль играет частие в таких обсуждения х слабоуспенвающих чеников, которые могут проя вить в них свою творческую активность [14].
1.2.5 Формулировка определений на основе классификации
Классификация естественно приводит к определению. Покажем это на примере рока с 15-летними чениканми, с которыми предварительно было изучено поня тие изометрии как преобразования лплоскости в плоскость [14], сохраня ющего расстоя ния , а также поня тие осевой симнметрии как особого рода изометрии, имеющей ровно одну пря мую неподвижных точек. Другие примеры изонметрии с чащимися еще не рассматривались в основнном курсе геометрии, но из пропедевтического курса они знали о физическома движения , имели нагля дные представления о параллельном переносе и повороте на плоскости.
На роке читель объя снил, что любая изометрия плоскости я вля ется осевой симметрией или результатом последовательного выполнения двух или трех осевых симметрии. Эту теорему он предложил использовать для классификации множеств изометрий на основе конличества и взаимного расположения осей симметрии. Попытка достигнуть цель привела к возникновению основ будущей классификации (рисунок 1.5).

Рисунок 1.5 Ца Классификация изометрий
Учитель подчеркнул, что некоторые из позиций этой таблицы могут содержать одинаковые преобразования .
Классификация нуждается в исключении таких случанев. На чертежах чащиеся рассмотрели поочередно все позиции и пришли к следующим выводам:
I - множестнво осевых симметрий;
II - множество параллельных пенреносов;
- множество нетождественных поворотов.
Множества IV и VII оказались пустыми. чащиеся виндели, что композиция трех осевых симметрии с ося ми, имеющими общую точку или параллельными, я вля ется осевой симметрией. Множество V ученики описали как состоя щее из последовательного выполнения параллельнного переноса и осевой симметрии. Относительно мнонжества VI было становлено, что оно состоит из повонротов с последующей осевой симметрией.
Дальнейшее исследование,
однако, показало, что каждый поворот с последующей осевой симметрией можно представить как параллельный перенос с последующей осевой симметрией. В конечном итоге классинфикация
множества изометрий свелась к позиция м
I, II, и V (причем позицию V надо дополнить словием  , которые определили нечто вроде геометрии симнметрии [25]. читель задал вопрос: Как можно было бы определить в рамках этой классификации (лнашей геонметрии)
параллельный перенос и поворот? В ответ ченики сформулировали определение, основанное на композиции осевых симметрии. Такое определение я винлось одним из проя влений математизации,
направлеой н использование приня той классификации.
, которые определили нечто вроде геометрии симнметрии [25]. читель задал вопрос: Как можно было бы определить в рамках этой классификации (лнашей геонметрии)
параллельный перенос и поворот? В ответ ченики сформулировали определение, основанное на композиции осевых симметрии. Такое определение я винлось одним из проя влений математизации,
направлеой н использование приня той классификации.
1.2.6 Формулировка определения путем выделения частного случая
Старшеклассникам, познакомившимся с тетраэдром, читель предложил выделить особые, интересные, по их мнению, виды тетраэдров. Поступили предложения :
- равнобедренный тетраэдр, то есть тот, у которого в однной вершине сходя тся три равных ребра (аналог равннобедренного треугольника);
- равносторонний тетраэдр, значит, имеющий только равные ребр (аналог равностороннего треугольника);
- пря моугольный тетраэдр, имеющий такой трехграый гол, у которого каждые два ребра перпендикунля рны (аналога пря моугольного треугольника).
Учитель сказал, что эти определения в математике не приня ты, но выделенные чениками формы заслунживают внимания , поскольку изучение таких тетраэднров приводит к интересным наблюдения м.
Например: в пря моугольном тетраэдре квадрат площади грани, пронтивоположной трехгранному глу с пря мыми плоскинми глами, равен сумме квадратов площадей остальнных граней. Это аналог теоремы Пифагора для тетнраэдров.
1.2.7 Формулировка определения посредством обобщения известного определения
Объя сня я на уроке поня тие предела функции в точнке, учитель рассмотрел функцию

и сравнил ее с функцией Дирихле:
|
|
|
|
|
Ученики заметили основную разницу: первая функция в каждой точке имеет левый и правый пределы (в иннтуитивном смысле), но они не совпадают. читель сонобщил, что в математике имеются соответствующие тернмины, и назвал их, определения предложил сформулировать самостоя тельно. Модифицируя определение предела функции на промежутке путем лослабления соответствующих условий, чащиеся получили формунлировку нового определения Ц предела функции в точке.
Приведенные примеры не исчерпывают всех ситуаций, способствующих формированию у чанщихся умения давать определения поня тий. Они, однанко, показывают возможности включения чеников в разнообразную дея тельность, заслуживающую вниманния и чителей, и методистов. Сказанное не означает, что при обучении нельзя знакомить учеников с готовынми определения ми. Наоборот, оба пути равноправны. В любом случае правильно организованная дея тельнность чеников служит для них школой применения я зыка математики, элементов математического метода, некоторых эвристических приемов.
Описанные приемы работы с определения ми в больншей мере относя тся к старшим классам средней шконлы. Но осторожно вводить соответствующие методиченские приемы можно и раньше. Не следует только стренмиться к преждевременной формализации и настаинвать на этих приемах в случае, когда они не оправндывают себя . Это относится также и к самостоя тельнной формулировке определений чениками. Недостатнкам, присущим чрезмерной формализации, не следует противопоставля ть сложности, свя занные с организациней математического творчества. К спеху может привенсти только разумное сочетание формализованных и эвнристических сторон в обучении математике.
1.3 Формирование математических поня тий у учащихся
Цель этого пункта - показать, кик конструинруется собственно методическая концепция формиронвания математических поня тий, которая отлична как от логических, так и от психологических теорий обранзования поня тий, хотя при ее конструировании испольнзуются и логика, и психология [28].
Рассмотрение этого вопроса важно и потому, что мственное развитие, в сущности, и есть способность переосмысливать старые и генерировать новые поня нтия . В контексте сказанного приоритетной проблемой теории и методики обучения математике я вля ется пронблема формирования поня тий.
Обратимся прежде к логическим теория м, описыванющим процесс формирования поня тий. Опишем три основные концепции [28].
I концепция . Процесс конструирования поня нтия протекает как поиск всех необходимых словий, которых достаточно для однозначного определения тренбуемого класса объектов.
Пример. Каждое из словий: "быть четырехугольнинком", "иметь равные стороны", "иметь равные глы" - тольнко необходимо для определения квадрата. Любая пара назваых словий также только необходима. Но все вместе они необходимы и достаточны для определения класса квадратов.
При определении поня тии часто используют ближайшее родовое по отношению к нему поня тие. Таким поня тием для квадрата я вля ется поня тие пря моугольника (ромба). учитынвая это, можно дать более экономное определение квадрата как пря моугольника с равными сторонами или ромба Ч с равными глами. В контексте данного логического подхода содержание поня тие отождествля ется с его определением [20].
II концепция . Поня тие рассматривается как лонгическая функция , заданная на множестве суждений и принимающая значения "истинно" или "ложно" [7]. Образование поня тия заключается в поиске его необходимых словий. В данной концепции единицей содержания поня тия выступает отдельное необходимое условие, потому содержание поня тия не совпадает с его определением.
концепция . Под содержанием поня тия поннимают сообщаемую им (семантическую) информанцию [23]. Единицей содержания выступают классы объекнтов, исключаемые поня тием из ниверсума, т.е. из мнонжества объектов, в терминах которого определя йся рассматриваемое поня тие [29].
Примеры
1 Пусть И - множество натуральных чисел, - словие, определя ющее делимость натурального числа на 2. Данное словие делит ниверсум, т.е. множество натуральных чисел, на два взаимоисключающих и совместно исчерпывающих ниверсум класса:
И
где А - множество чисел, деля щихся на 2;
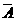 а- множество чисел, не деля щихся на 2.
а- множество чисел, не деля щихся на 2.
Условие определя ет поня тие лмножество четных чинсел. Это поня тие исключает класс 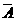 , поэтому содержание поня тия лмножество четных чисел равно классу
, поэтому содержание поня тия лмножество четных чисел равно классу 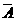 его составля ет класс А.
его составля ет класс А.
2 Пусть И - множество четырехугольников, - словие лиметь равные стороны, в - лиметь равные глы. словие разбивает ниверсум (множество И) на класс четырехнугольники с равными сторонами (А) и его дополнение - класс четырехугольники с неравными сторонами (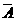 . снловие в разбивает множество А на классы: четырехугольнники с равными сторонами и равными углами (В) и четырехугольники с равными сторонами и неравными глами" (
. снловие в разбивает множество А на классы: четырехугольнники с равными сторонами и равными углами (В) и четырехугольники с равными сторонами и неравными глами" ( ). Класс
). Класс
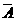 а(четырехугольники с неравными сторонами) словием в разбивается на класс С - четырехугольники с неравными сторонами и равными глами и класс
а(четырехугольники с неравными сторонами) словием в разбивается на класс С - четырехугольники с неравными сторонами и равными глами и класс  Ч четырехугольники с неравными сторонами и неравными гнлами.
Ч четырехугольники с неравными сторонами и неравными гнлами.
Содержание поня тия квадрат эквивалентно сумме класнсов  . Объемом поня тия я вля ется
класс В. свонить поня тие квадрат - это, прежде всего, меть распознанвать четырехугольники, образующие классы В,
. Объемом поня тия я вля ется
класс В. свонить поня тие квадрат - это, прежде всего, меть распознанвать четырехугольники, образующие классы В,  , С,
, С,  , выводить следствия из принадлежности четырехугольника одному из казанных классов и строить четырехугольники, относя щиеся к данным классам. В процессе выполнения
пенречисленных действии сваивается
информация , выделя ющая квадраты из множества четырехугольников,
т.е. словесная формулировка определения
поня тия
[13].
, выводить следствия из принадлежности четырехугольника одному из казанных классов и строить четырехугольники, относя щиеся к данным классам. В процессе выполнения
пенречисленных действии сваивается
информация , выделя ющая квадраты из множества четырехугольников,
т.е. словесная формулировка определения
поня тия
[13].
Наблюдения за работой учителей математики принводя т к выводу о том, что формирование математичеснких поня тий в школе не вписывается в чистом виде ни в одну из описанных выше логических концепций. Но элементы каждой из них присутствуют в практике обунчения математике. Такое положение можно объя снить тем, что логические концепции сами по себе далеко не исчерпывают всех составля ющих процесса формированния поня тия . Они не могут объя снить чителю, каковы этапы формирования поня тия , какие мственные дейнствий адекватны каждому этапу.
Эти вопросы исследуются в психологии, где, в часнтности, отмечается значимость овладения следующими мственными действия ми: подведением объекта под поня тие (распознавание), отысканием следствий (из факта принадлежности объекта поня тию). Так, Н.Ф.Талызина к компонентам указанных мственных действий относит: перечисление необходимых и достаточных свойств объектов данного класса; установление того, обладает ли данный объект выделенными свойствами или не обладает; заключение о принадлежности объекта к данному поня тию; выведение следствий; классифинкацию; конструирование объектов с четом варьиронвания отношений [32]. а
Ря д психологов (Н.А. Менчинская , Е.Н. Кабанова - Меллер и др.) рекомендуют при формировании поня тий осуществля ть варьирование несущественных признаков, тем самым способствуя своению существенных.
Овладение действием предполагает адекватную ему задачу, поэтому конструирование системы задач, оринентированных на усвоение поня тия , я вля ется весьма важной проблемой для такой науки, как методика пренподавания математики. Однако не все авторы учебнинков математики для школы должным образом пониманют эту проблему.
Рассмотрим например, поня тие "вненшний угол треугольника". Ни в учебнике Л.С. Атанася на и др. "Геометрия 7-9" [8], ни в учебнике Л.С. Анатася на "Геометрия 10-11" [9] нет задач на распознавание и констнруирование внешних глов треугольника. Причем как в одном, так и в другом учебнике приведены задачи, реншение которых основано на теореме о внешнем гле треугольника. Возникает вопрос: будут ли ченики, обучающиеся по названным учебникам, допускать ошибнки в распознавании внешнего гла треугольника?
С целью получения ответа было проведено наблюденние [28].
На роке опытная учительница много внимания деля ла построению внешнего гла треугольника, принчем использовала не только стандартные ситуации. ченики строили и глы, расположенные под горизоннтальной стороной треугольника.
В конце рока наблюдающий предложил ребя там ответить на вопрос: "Какой из глов - 1, 2 или 3 - я вля ется внешним глом треугольника ABC на рисунке 1.6?"

Рисунок 1.6 - Распознавание внешнего гла треугольника
Лишь один из 33 учащихся класса назвал гол 3. Причина я сна: ченики стронили объекты, принадлежащие данному поня тию, не выполнив предварительно ни одного пражнения на распозннавание объектов, т.е. на подведение под поня тие [28]. С точки зрения логики в качестве определения монгут быть приня ты различные системы необходимых и достаточных свойств поня тия . Поэтому в методике возникает вопрос о выборе такой системы. Например, поня тие параллелограмма в различных учебниках геонметрии определя ется по-разному: четырехугольник, у которого противоположные стороны попарно паралнлельны; пересечение двух полос с непараллельными края ми;а четырехугольник, имеющий центр симметнрии, и т.д.
С точки зрения методики, приведенные определения неравноценны. Они обладают разной стенпенью нагля дности, т.е. определя емый объект по-разнному просматривается через определения . Учитывая значимость образного компонента в процессе форминрования поня тия , методисты должны заключить, что в школьном курсе математики желательны такие опренделения , которые позволя ют воображению легко коннструировать образы определя емых объектов. С точки зрения указанного требования наиболее дачным я внля ется традиционное определение параллелограмма. Такой вывод согласуется с результатами психологичеснких исследований: в свернутом виде распознавание может осуществля ться по внешне выраженным, нагля днным признакам используемых объектов, не по тем признакам, по которым оно осуществля лось на ровне развернутого выполнения действия [20].
Опишем теперь методические требования к форминрованию поня тия [28].
Начальным этапом я вля ется мотивация . Сущнность этого этапа заключается в подчеркивании значинмости рассматриваемого поня тия , и возбуждении интенреса к нему. Мотивация может осуществля ться как понсредством привлечения средств нематематического сондержания , так и в ходе выполнения специальных пнражнений, объя сня ющих необходимость развития матенматической теории. Например, поя вление обыкновеых дробей, как правило, мотивируется потребностя ми практики. Введение смежных глов можно объя снить рассмотрением не только отдельных фигур, но и их обънединений. Рассмотрение взаимного расположения пря нмой и окружности приводит к трем случая м, один из которых характерен тем, что окружность и пря мая именют только одну общую точку. казанный случай и обуснловливает введение поня тия касательной к окружности.
Следующий этап - выя вление существенных свойств поня тия , которые составя т его определение. Он реализуется в основном посредством пражнений [28]. Например:
1 Арифметическая и геометрическая прогрессии могут быть введены путем выполнения пражнений на запись чиснловых последовательностей, заданных определенными свойствами, либо на выя вление свойств, которыми обладают казанные последовательности.
2 Ознакомление с существенными свойствами трапеции может осуществля ться следующим образом. Заранее готовится рисунок 1.7.




а) б) в) г)





д) е) ж) и) к)
Рисунок 1.7 - Задание к ознакомлению с существенными свойствами трапеции
Рассматривая этот рисунок, учащиеся должны ответить на вопрос: "Какие из данных фигур имеют общие свойства?" Ребя та замечают, что в четырехугольниках а, б, г, д, и, к две противоположные стороны параллельны, две другие - нет. После этот им сообщается , что такой четырехугольник назынвается трапецией. Введение поня тия трапеции может быть осунществлено и путем выполнения пражнений на построение разнличных четырехугольников, в том числе и четырехугольников, у которых две стороны параллельны, две другие - нет.
Итогом этого этапа я вля ется формулировка опреденления поня тия . Еще раз подчеркнем, что на рассмотнренном этапе термин обозначает не столько поня тие, сколько соответствующие нагля дные представления .
На этапе своения объектом изучения
долнжно стать каждое существенное свойство, используенмое в определении. Обеспечивается это требование с помощью пражнений, в частности на распознавание объектов,
принадлежащих поня тию. Пусть,
например, и вЧ видовые отличия
поня тия
А,
соединенные конъюнктивной свя зкой,
т.е.  .
.
Тогда словие непринадлежности поня тию А имеет вид:  . Зная
условие принадлежности и неприннадлежности поня тию,
нетрудно сконструировать пнражнения ,
формирующие действие распознавания
объектов, принадлежащих поня тию. Это пражнения вид
. Зная
условие принадлежности и неприннадлежности поня тию,
нетрудно сконструировать пнражнения ,
формирующие действие распознавания
объектов, принадлежащих поня тию. Это пражнения вид 
Примеры
Проиллюстрируем конструирование пражнении на принмере поня тия биссектрисы гла [20]. Логическая структура опренделения этого поня тия такова:
 |
|
Луч ОС -
биссектриса гла АОВ |
(1) луч ОС исходит из вершины гла АОВ |
|
(2) луч ОС делит гол пополам |
Исходя из структуры определения , осуществля ем констнруирование упражнений:
1 Луч ОС исходит из вершины гла АОВ, a  AOC
AOC  COB. Явля ется ли луч ОС биссектрисой гла АОВ? ((1)
COB. Явля ется ли луч ОС биссектрисой гла АОВ? ((1) 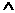 а(
а(
2 Некоторый луч делит угол пополам, его начало не совпадает с вершиной гла. Явля ется ли луч биссектрисой данного гла? ((2)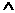

3 Луч ОС исходит из вершины гла АОВ и делит ею понполам.
Явля ется ли луч ОС биссектрисой гла АОВ? ((1)  а(2).)
а(2).)
При конструировании казанных пражнений слендует предусмотреть и вариативность расположения объектов (см. пример с внешним глом треугольника), так как применение действия в одной ситуации не гарантирует спех при его применении в другой ситуанции, отличной от первой [28]. Отразить это требование в словесно заданных пражнения х невозможно, поэтому используют пражнения на готовых чертежах. Выполння я такие пражнения , учащимся приходится вычлення ть на рисунках объекты, принадлежащие данному поня тию, рассматривать объекты с точки зрения других поня тий.
По отношению к поня тию биссектрисы гла обсуждаемая система пражнений на готовых чертежах монжет быть представлена следующим вопросом:
Какие из лучей, обозначенных на рисунке 1.8, я вля ются биссектнрисами данных глов?





) б) в) г) д)





е) ж) и) к) л)
Рисунок 1.8 - Рисунок к пражнению для определения поня тия биссектрисы гла
Другим действием, адекватным содержанию поня нтия , я вля ется действие выведения следствий из приннадлежности объекта поня тию [13].
Пример
Известно, что четырехугольник MNPQ - транпеция (NP и MQ - ее основания ). Назовите следствия , вытенкающие из данных словий в силу определения трапеции.
Необходимы комплексные упражнения , выполнение которых основано не только на использовании сущенственных свойств поня тия , но и на отыскании следствий.
Примеры
1 Известно, что некоторый луч исходит из вершины гла. Следует ли отсюда, что этот луч я вля ется биссектрисой гла? Если нет, то измените словие так, чтобы из него следовало, что луч я вля ется биссектрисой данного гла.
2 Луч ОС исходит из вершины гла АОВ,
 AОC
AОC
 В.
В.
Явля ется ли луч ОС биссектрисой гла АОВ? Если нет, изменните словие так, чтобы луч ОС я вля лся биссектрисой гла АОВ.
Следующий этап - использование поня тия в конкретных аситуация х [28]. На этом этапе, прежде всего, осуществля ется знакомство со свойстванми и признаками поня тия , с его определения ми, эквинвалентными приня тому; используются изученные свойства и признаки поня тия .
Учащиеся сваивают мение переходить от поня тия к его существенным свойствам и обратно, переосмысливают объекты с точки зрения других поня тий, в частности чатся переосмысливать элементы чертежа с точки зрения другой фигуры и т.д. Здесь важно использовать блоки задач, объединенных какой-либо общей идеей [20].
Упоря дочение задач может быть осуществлено понсредством обобщения и конкретизации, привлечения аналогии, взаимно обратных задач.
Блоки задач могут конструироваться следующими способами:
) результаты решения предыдущей задачи испольнзуются в решении последующей;
б) результаты решения предыдущей задачи испольнзуются в условии последующей;
в) предыдущие задачи я вля ются элементами послендующей;
г) решение совокупности задач осуществля ется однним и тем же методом.
С блоками задач можно ознакомиться по статья м Г.И. Саранцева [27]. Организация задач в соответствии с казанными направленния ми возможна даже в рамках действующих учебнинков, однако полная их реализация требует существеой доработки задачного материала, как в его содержаннии, так и в последовательности расположения . При этом оказывается , что многие задачи могут быть составлены самими чащимися , что важно в плане иннтеллектуального развития чеников.
В изучении любого учебного предмета, и особенно математики, важен этап систематизации мантериала, когда выя сня ется место данного поня тия в системе других поня тий.
Это достигается следующими путя ми [28]:
- становлением свя зей между отдельными поня тия нми, теоремами;
- разноплановой систематизацией материала по различным основания м;
- обобщением поня тия ;
- конкретизацией поня тия .
В качестве средств представления информации в сжатом виде используют таблицы, вопросники, графинки, рисунки, схемы, обобщающие рефераты и т.д.
Учитывая , что пражнения я вля ются основным среднством формирования поня тий в средней школе, сопостанвим в виде таблицы каждый этап формирования поня тия и соответствующие ему виды пражнений (таблица 1):
Таблица 1 - Этапы формирования поня тия и соответствующие ему виды пражнений
|
Этапы формирования поня тия |
Упражнения , реализующие их |
|
Мотивация введения поня тия |
|
|
Выделение существенных свойств поня тия |
|
|
Усвоение логической структуры определения поня тия |
Упражнения с моделя ми фигур
Упражнения на дополнение словий (распознавание и выведение следствий) |
|
Применение поня тия |
|
|
Установление свя зей изучаемого поня тия с другими поня тия ми |
|
Итак, процесс формирования математических поня нтий в средней школе оказывается более сложным по сравннению с его видением на основе логики и психологии. Поэтому очень важно после формирования математических поня тий продиагностировать ровень сформированности.
2 Экспериментальные исследования при диагностике математических поня тий у учащихся
2.1 Значение вопроса при диагностике математических поня тий у учащихся на роках математики
Учителя на роках много задают вопросов чащимся . Тем самым они преследуют несколько целей [30]:
- активизируют внимание учащихся всего класса,
- выя сня ют знание учебных тем,
- подсказывают верный ход решения задачи,
- точня ют ответы учащихся .
Но продуманная и точная постановка вопроса может служить также диагностике математических поня тий у учащихся . Поя сню мысль на нескольких примерах [31].
Урок геометрии в IX классе. Тема Абсолютная величина и направление вектора. Первый час по теме отводился изложению нового материала. На втором часу - семинар. Идет опрос по всем определения м и теоремам. Цель учителя - выя снить, насколько прочно чащиеся своили обя зательные сведения . Вопросы чителя требуют от учащихся не рассуждений, а знания формулировок:
Какие полупря мые называются одинаково направленными?
Сформулируйте и докажите теорему об одинаково направленных полупря мых. И т. д.
Но же здесь можно ставить вопросы, ответа на которые ченики не найдут в готовом виде в учебнике. Им нужно хорошо понимать смысл определений, их свя зь и назначение. Например: для чего мы вспомнили полупря мые в теме о векторах?
Предполагаемый ответ: так как направленность векторов определя ется через направленность полупря мых - рождает новый вопрос: почему мы не можем определить направленность векторов через параллельный перенос, как мы это сделали для полупря мых?
Ответ требует же серьезных размышлений. Мы должны сравнить вектор с полупря мой. Только ли одинаково нанправлены будут векторы, если они совместя тся параллельным переносом? Имеет ли длину полупря мая ? А почему нельзя определить направленность через пря мые, которые будут совмещаться при параллельном переносе?
Подобные вопросы глубля ют поня тия учащихся о векторах, раскрывают структуру построения математических поня тий [31].
На роке после темы Координаты вектора желательно вновь повторить определения и хотя бы формулировки всех теорем о векторах. Нужно помнить, что для учащихся это не жизненно необходимые знания . Для них они инородны и быстро забываются . Но вопросы же можно формулировать в другом виде. Например, после вопроса на повторение: какие векторы называются равными? - можно спросить: А при доказательстве каких теорем используется определение равенства векторов? Чтобы ответить на вопрос, даже только сформулировав теоремы, надо хорошо знать, главное, понимать доказательство. Так что знание доказательств можно проверить, не выслушивая всего доказательства. Кроме того, у учащихся систематизируются знания , что делает их более осмысленными и прочными.
Рассмотрим еще пример. Здесь постановка вопросов носит несколько иную смысловую нагрузку [31].
Урок математики в V классе. Тема Вычитание. На этом роке ребя та впервые встречаются с точным математическим определением. Желательно заострить на этом моменте внимание учащихся , чтобы создать верный импульс в развитии математического мышления .
Вычесть из одного числа другое ребя та могут. Этому их чили с I класса. Но вот как они отвечают (и не могут ответить иначе) на вопрос: что значит: из числа вычесть число в?: это значит: из вычесть в; это значит: меньшить число на в единиц; это значит: найти разность чисел а и в. Они понимают, кака найти разность чисел и в, но не отвечают на поставленный вопрос. Запишем определение: вычесть из числа чиснло в - значит найти такое число х, которое в сумме с в дает а. Вопрос к ченикам: почему это довольно сложное предложение можно считать определением, ванши ответы - нет?
Молчание.
Учитель: Когда вы пытались определить вычитание, вы потнребля ли слова, которые сами требуют определения . Нанпример: лотня ть, луменьшить, найти разность. А ченрез какое поня тие определя ется вычитание?
Кто-то догадывается :
-а Через сумму.
Учитель: Очень хорошо! Верно! Вычитание определя ется ченрез сложение. А сложение?
Следуют ответы, но неверные. Наконец:
- Ни через что не определя ется .
Учитель: Верно. Сложение - одно иза первоначальныха поня нтий математики и понимается нами н основе нашего жизненного опыта. все остальные арифметические действия так или иначе (деление - косвенно) определя ютнся через сложение.
Еще хочется привести пример типичных ошибок учащихся , их выя вление и исправление [1].
Учитель показывает чертеж пря моугольного треугольника, пря мой гол которого изображен при вершине, не у основания , как чащиеся привыкли видеть в учебниках. Оказалось, что отдельные ченики (7-й класс) не узнают в чертеже пря моугольный треугольник, хотя на чертеже указано. Что гол при вершине равен 900, остальные два гла равны соответственно 600 и 300. Они заходя т в тупик: вроде бы не похож треугольник на пря моугольный, а то же время есть у него гол 900. причина затруднения - расхождение в их сознании поня тийной и образной характеристик объекта, т. е. хотя и наличествует пря мой гол, но на чертеже дано не то. Недоумение и ошибочный ответ вызваны тем, что определение поня тия а и нагля дный образ объекта (по чертежу в учебнике) запомнились, т. е. все это заучено, но осталось неусвоенным научное содержание геометрического поня тия пря моугольный треугольник, у которого один существенный (необходимый и достаточный) признак - наличие пря мого гла, где он может находится на чертеже, значения не имеет. Такие же затруднения вызывают непривычные изображения любых других геометрических фигур. Как странить такое распространенное я вление, как плохое своение поня тий, приводя щее к ошибкам при выполнении учебных действий? Надо приучить учащихся к самым различным нагля дным изображения м объекта изучению при которых не искажалась бы сущность научного поня тия . Когда ченики прорешают достаточно много нешаблонных задач, они привыкнут анализировать их с точки зрения теории и не окажутся в тупиковой для себя ситуации. Тогда они, встретив непривычное изображение или незнакомое название предмета. Не будут в растеря нности, сразу начнут сравнивать его признаки с признаками изучаемого в данный момент научного поня тия .
Или другой пример [20]. Правильно ответив на вопрос, под каким углом пересекаются диагонали ромба (лпод пря мым), ченик не может уверенно ответить на простой вопрос, свя занный с первым: Диагонали четырехугольника пересекаются взаимно перпендикуля рно. Может ли данная фигура быть ромбом? Он или отказывается от ответа, или отвечает на него отрицательно, то есть неверно. Некоторые ченики вообще не видя т разницы в содержании вопросов, считают, что это один и тот же вопрос. Причина затруднения и ошибок - в недостаточном развитии мышления , в частности, в неумении логически мыслить и вводить новое знание из ранее известного, также формально заученное знание данного конкретного вопроса - о пересекающихся диагоналя х ромба. Как преодолеть подобные ошибки? Можно продолжать постановку нестандартных вопросов, требующих мышления . Так, например, этот же вопрос можно повернуть и по - другому: если на него (в приведенном варианте) ученик ответил твердительно, т. е. правильно, то следует вопрос: А может быть, это квадрат, не ромб, так как у него ведь тоже диагонали пересекаются под пря мым углом? своивший теорию ченик отвечает веренно, что квадрат - это тоже ромб, но не только с равными сторонами, но и с пря мыми углами.
Попытка чителя возразить ему, сравнивая определения поня тий лромб и квадрат, не произвела не него впечатления : он продолжал настаивать, тверждая : Определение квадрата не противоречит определению ромба. Тогда читель говорит: ведь у ромба нет такого признака, как пря мые углы?, на что у ченика немедленно находится ответ: Ну и что? В определении квадрата зато есть все признаки ромба; равные стороны и взаимно перпендикуля рные диагонали. Разгоревшая ся дискуссия вызвала интерес у всех чеников в классе, но с прозвеневшим звонком она была прервана. читель расстался с учениками, не разрешив дискуссионную проблему, но попросил их внимательно подумать на досуге, в чем тут дело. В следующий раз вернемся к этому вопросу, - пообещал он. Можно быт уверенным, что ченики будут обя зательно думать и спорить и непременно придут к каким - то своим выводам, правильным или не совсем. На очередном роке читель поставил все точки над i, рассудит, кто прав или не прав, и объя снит, почему. И объя снение его ля жет на же подготовленную психологическую почву - созревшую психологическую готовность чеников знать истину - ответ на спорный вопрос.
2.2 К вопросу о диагностике математического поня тия "величина"
Под руководством В.В.Давыдова группой методистов было, разработано содержание дочислового периода и выделены основные способы действия по формированию математического поня тия величины [10].
Критерием понимания величины как особого свойства предметов я вля ется то, что при оценке отношений между реальными объектами чащиеся отказываются от непосредственных суждений, выделя ют общий для сравниваемых предметов признак и с помощью него станавливают соответствующие отношения между величинами (<, >, =) [21].
В подходе Б.Д. Эльконина к логико-психологическому строению поня тия величины как свойства предметов недостаточно для полноценного формирования поня тия величины [36]. Поня тие величины необходимо рассматривать через отношение двух основных действий: сравнение и преобразование, которые задаются при аксиоматическом определении математической величины. Таким образом, в подходе Б.Д. Эльконина, критерием сформированности поня тия "величина" становится мение ребенка с помощью предмета-посредника (разницы) рассматривать отношение между величинами через их изменение, т.е. уметь переходить от сравнения к преобразованию и обратно.
анализ методических разработок по математике (экспериментальная программа В.В. Давыдова), проведенный с точки зрения на величину как отношение действий, показал, что в обучении детя м недостаточно представлена знаковая характеристика поня тия величины. Ориентируя сь на отношения <, >, =, чащиеся осуществля ют разностное сравнение предметно представленных величин, однако само разностное отношение не я вля ется особым предметом действия . Другими словами, чащиеся не выстраивают переход от сравнения к преобразованию с опорой на разницу. Недостаточная разработка подхода к введению величины как совокупности параметров объекта ограничивает возможности учащихся в освоении полного поня тия величины.
Задача настоя щего исследования состоя ла в том, чтобы определить, каким образом содержание поня тия "величина" представлено в действия х детей.
При конструировании диагностических методик я опиралась как на нормативные характеристики поня тия [37], выделенные в результате логико-психологического анализа, так и на требования к построению системы диагностических заданий [19], [15].
В соответствии с критерием предметности теоретического знания необходимо было выделить как существенные признаки поня тия , так и несущественные для объективного содержания поня тия признаки. Создание в экспериментальной ситуации ориентации ребенка на несущественные признаки, присутствующие в реальной ситуации решения задачи, позволит определить, что я вля ется содержанием действий ребенка и совпадает ли оно с содержанием поня тия [21].
Следовательно, общий принцип построения экспериментальной ситуации должен состоя ть в противопоставлении двух возможных способов действия учащегося : натурального отношения к объекту и теоретического отношения к нему.
Если окажется , что ровень знаний, определенный по диагностическим методикам, не соответствует нормативным критерия м сформированности математического поня тия "величина", то можно будет сделать вывод о том, что существующая система заданий в экспериментальной программе по математике не совершенна и не приводит к полному формированию поня тия .
С целью определения сформированности поня тия "величина" в соответствии с нормативными характеристиками я применя ла методику "Полоски" [21].
Задания , представленные в методике, позволя ют выя вить, выступает ли для учащихся отношение между величинами (разница) как предмет преобразования - перехода от одной величины к другой. Следовало определить, могут ли дети представить отношение А > В через отношение А = В + С, т.е. дискретное отношение между двумя объектами рассмотреть через непрерывное преобразование одной величины (А) из другой (В).
Кроме того, сконструированная методика необходима для того, чтобы выя вить, меют ли чащиеся моделировать процесс преобразования величин. Процесс преобразования величины в задания х методики был представлен двумя планами: предметным (ря д бумажных полосок) и символическим (формулы, описывающие процесс преобразования ). То, насколько ребенок различает эти два плана и может переходить от одного к другому, позволя ет судить о сформированности действия моделирования .
Основной принцип построения методики состоя л в выделении и представлении отношения между двумя действия ми: с одной стороны, преобразованию объекта противопоставля лось сравнение двух объектов как отдельных вещей, с другой стороны, объекты предъя вля лись, "как будто" разные состоя ния изменения одного объекта [24].
Процесс преобразования был задан возрастающим ря дом бумажных полосок. С помощью формулы, описывающей преобразование, требовалось из данного ря да бумажных полосок путем попарного сравнения их между собой выделить отношение между ними (разницу). Трудность данного задания состоя ла в том, что разницы были отмечены в формуле буквами, однако не были представлены нагля дно. Требовалось восстановить разницу как способ перехода от одной величины к другой. Именно в таких задания х разница, представленная как отношение между двумя величинами, найденная путем сравнения их между собой, позволя ет восстановить действие преобразования через сравнение, т.е. выступает как знак, фиксирующий отношение двух действий.
Эксперимент проводился в сентя бре-октя бре 2006 года. Испытуемыми были 22 ченика 3 класса экспериментальной школы № 3 в поселке Комсомольском Чамзинского района.
Материалом для методики послужили четыре бумажные полоски разной длины, расположенные в поря дке возрастания по длине (рисунок 2.1).
 |
γ б γ в γ аг
Рисунок 2.1 Ца Расположение материала задания Полоски
Экспериментатор предъя вля л инструкцию, в которой содержалось объя снение процесса преобразования : "У меня есть резиночка, которая все время растя гивается . Сначала она была такая (показывает на меньшую полоску в начале ря да), затем такая (показывает на следующую), потом вот такая (третья полоска в ря ду) и, наконец, стала такая (показывает на самую большую полоску)". Далее экспериментатор записывал под ря дом полосок формулу γ б γ в γ г и задавал следующие вопросы:
- Покажи на полосках, где а, б, в, г.
- С помощью какого математического действия можно написать про растя жение резиночки?
Если испытуемый не мог ответить на вопрос о действии, то экспериментатор записывал следующую формулу под предыдущей (рисунок 2.1) и давал объя снение: "Растя жение резиночки из "а" в "г" я описала через сложение". После этого экспериментатор предъя вля л ря д заданий.
Задание 1. В данном задании требовалось найти отношения (разницы) между бумажными полосками, обозначенные в формуле буквами. "Покажи на полосках, где м, к, о, е?"
Задание 2. Требовалось по записанным формулам к+о, о+е, к+е найти в предметном плане сумму разниц: "Что значит сумма к+о? Покажи на полосках".
Задание 3. В данном задании требовалось найти соответствие между формулой, замещающей ря д полосок, и формулой, моделирующей процесс изменения длины резиночки. "Давай с тобой поиграем, - говорил экспериментатор, - Мы должны получить одинаковый результат, работая с разными формулами. Я буду работать с формулой γ б γ в γ г, а ты с формулой м + к + о + е. Я из "б" получаю "в" (показывает на часть формулы б - в), ты? Покажи часть своей формулы, по которой получится тот же результат, что и у меня ". Испытуемый должен показать часть формулы, соответствующей результату изменения по формуле экспериментатора.
Результаты.
В эксперименте участвовало 22 ченика. Из них со всеми задания ми справились 3 человека (13%). С первым заданием 50% детей справились самостоя тельно, 50% лишь после наводя щих вопросов экспериментатора перешли от неверного решения к верному.
Верным способом решения задания 1 я считала такое поведение испытуемых, когда они по формуле сложения могли выделить разницу из предметного ря да полосок. Отличительным признаком такого поведения я вля лся жест испытуемого; пальцами показывается расстоя ние, на которое отличаются соседние в ря ду величины (рисунок 2.2).
 |
е
о
к
б в г
Рисунок 2.2 - Выделение разниц в задании 1
Я наблюдала типичное поведение при неправильном решении задания . Испытуемые казывали, как правило, на полоски и не пытались находить отношение между величинами. В этом случае формула м + к + о + е ничем не отличалась от формулы γ в γ с γ д.
Экспериментатор просил ребенка по формуле сложения выполнить действие с полосками. Испытуемый прикладывал полоски по длине в одну линию (рисунок 2.3).

м к о е м+к+о+е
Рисунок 2.3 - Отождествление разниц с полосками
После того, как экспериментатор спрашивал, до какой длины растя гивалась полоска, чащиеся беждались, что они неверно нашли величины и нарушили словие задачи.
Важно отметить, что такая подмена словий задания свидетельствует о том, что испытуемые непосредственно соотнося т предметы и буквенное обозначение величин, не обращая внимания на математический знак сложения . Если разница нагля дно не представлена, то испытуемые не могут ее выделить. В этом случае разница не я вля ется способом перехода от одной величины к другой, а выступает предметом - таким же, как и сравниваемые предметы.
При выполнении задания 1 я добивалась понимания и предметной фиксации разницы с помощью жеста (двумя пальцами испытуемый показывал тот отрезок, на который величивалась одна из полосок). После этого чащиеся переходили к выполнению задания 2. От общего числа испытуемых только 40% детей смогли правильно выполнить задание 2.
При верном решении мы наблюдали следующие способы поиска суммы разниц:
- либо чащиеся сначала показывали пальцами отрезок (разницу), а затем объединя ющим жестом присоединя ли отрезки друг к другу (рисунок 2.4, );
- либо полоски накладывались детьми одна на другую, общая разница выделя лась как часть одной из полосок (рисунок 2.4,б).

а) б)
Рисунок 2.4 - Варианты верного решения задания 2
При неверном выполнении задания наблюдалось два типа ответов. В первом случае за сумму разниц принималась одна из полосок (рисунок 2.5, а).
Во втором случае, когда экспериментатор просил показать сумму разниц, испытуемые показывали только одну из разниц (например, вместо о + е выделя лся отрезок о или е (рисунок 2.5, б.).
 |
о о+е к к+о к+е о+е о+е=е к+е=е
а) б)
Рисунок 2.5 Ца Варианты неверного решения задания 2
Видно, что в таких случая х испытуемые не могут работать с разницей. Даже если происходит верное выделение одной из разниц (случай 2), то испытуемый все равно не может найти сумму, т.е. предметно показать общее отношение. Эти данные свидетельствуют о том, что для детей не произошло отделение отношений от самих вещей, не существует вне предметов и должно быть представлено нагля дно.
Выполнение задания 3 оказалось самым трудным для учащихся , т.к. требовалось работать уже не в плане предметного ря да полосок, находить отношение между двумя видами записи одного и того же процесса преобразования величины резиночки.
Только 30% от общего числа испытуемых (6 детей) смогли верно выполнить это задание. Эти испытуемые действовали без опоры на предметный ря д и не принимали во внимание провоцирующий фактор, что одна формула записана точно под другой.
Напротив, для другой группы испытуемых из 18 частников эксперимента (70%) такая запись провоцировала на буквальное повторение действий экспериментатора, работающего с первой формулой.
Испытуемые совмещали части двух формул и отвечали, например, что переход от "в" к "г" означает, по их формуле, о+е (рисунок 2.6).
 |
а→б б→в в→г м+к к+о о+е
Рисунок 2.6 - Неверное соотнесение формул в задании 3
Оказалось, что значки " - " и " + " означают одно и то же действие: переход от одной вещи к другой.
Таким образом, обнаруженный факт натурального понимания разницы, отношение к ней как к вещи в ря ду других вещей означает, что процесс изменения вещей и процесс действий с отношения ми между вещами оказываются слиты в мышлении детей.
Итак, результаты проведенного эксперимента показывают, что к третьему классу обучения только 20% учащихся (выполнивших задание 1 и 2) могут не только выделить отношение, которое не представлено предметно, но и моделировать процесс преобразования этих отношений.
Однако 50% учащихся (по результатам решения заданий 1) не могут самостоя тельно выделить отношение между двумя предметами, т.е. не могут отделить отношение между вещами от самих вещей. Это позволя ет сделать вывод о преобладающем натуральном подходе в отношении к математическому поня тию "величина".
Данные эксперимента указывают на недостаточную разработку как логико-психологического анализа поня тия "величина", так и методического оформления заданий по формированию полноценного поня тия величины.
Уместно привести положение Б.Д. Эльконина о том, что знаковость как центральная характеристика поня тия величины не формируется спонтанно, должна стать объектом специального формирования [36].
Подтверждается мое предположение о том, что введение поня тия величины, основанное на действия х уравнивания и сравнения , недостаточно. Необходимо приня ть во внимание положение о том, что введение величины должно быть основано на отношении двух действий: сравнения и преобразования . Это положение требует поиска особой формы представленности для ребенка действия по преобразованию величины объекта, на основе которого возможно было бы осуществля ть переход к действию сравнения .
2.3 Диагностика ровня сформированности математических поня тий (метод ключевых поня тий)
В данном пункте описан метод ключевых поня тий, который, как представля ется , хонрошо отвечает задаче оценки сформированности поня тийного апнпарата. Содержание метода подробно обнсуждается в статье Н.О. Вербицкой, В.Ю. Бодря кова [4]. Он основывается на иснследовании остаточных знании учащихся по проверя емой теме, разделу, курсу.
Остаточными знания ми мы называем тот объем поня тий, которым лотложился , оснтался в памя ти учащихся после изучения темы спустя некоторое время , в течение которого эти поня тия с детьми не повторя нлись.
Важно подчеркнуть, что объем и структунра остаточных знаний напря мую свя заны с интеллектуальным ровнем развития ченинка.
Ученик с низким интеллектом менее восприимчив к теоретическим поня тия м, т. е. от него нельзя ожидать качественных и полных определений, которые вполне естественны для учащихся более высокого интеллекта [15]. Поэтому применению метода ключевых поня тий должны предшествовать псинхологические исследования интеллектуальнного развития каждого ченика. В литературе по психологии приня то выделя ть семь ровнней интеллекта: высокий, очень хороший, хороший, меренный, средний, довлетвонрительный, низкий. На методах становленния такой классификации мы останавлинваться не будем, поскольку он хорошо изнвестен специалистам. Методической оснонвой такой классификации может стать стандартный тест ШТУР (школьный тест мственного развития ), который часто встренчается в психологической литературе [12].
Суть самого метода ключевых поня тий довольно проста. чащимся предлагается письменно наиболее полно раскрыть от 5 до 10 основных поня тий, составля ющих суть диагностируемой темы. При этом предлангаемые поня тия должны отвечать требования м ключевого значения и достаточной общности [5].
В зависимости от объема проверя емого материала и сложности поня тий на письнменную работу может быть затрачено от 20 до 40 мин. Собрав работы, читель казыванет на каждой из них индивидуальный иннтеллектуальный балл ее исполнителя , зантем оценивает по 5-балльной системе каченство выполнения задания . На основе провенденной проверки вычисля ются следующие показатели:
ИУ - индивидуальный общий ровень знаний, показывающий, сколько процентов задания выполнил чащийся :

СУ - средний общий ровень знании, демонстрирующий, какая часть задания вынполнена в среднем в данной группе учащихнся :

На основе полученных данных вычисля нется главный показатель - индивидуальное расхождение (ИР). Это тот процент выполнненного задания , который соответствует ровню интеллекта каждого учащегося . Понказатель ИР определя ет, с одной стороны, индивидуальную лнедогруженность каждонго ченика и, с другой стороны, наибольнший возможный процент выполнения заданния (т. е. своенных поня тий) на нынешнем этапе мственного развития ученика. Если ченик имеет высокий ровень интеллекта и при этом сумел разъя снить всего 30% клюнчевых поня тий, то, значит, качество его знаний нуждается в срочном восполнении. Но если школьник имеет довлетворительнный ровень интеллекта, но сумел разъя сннить 80% заданных поня тий, то он заслужинвает отличной оценки, не те три балла, которые он обычно получает на контрольнной работе. Именно индивидуальное раснхождение должно определить оценку ребеннка при проверке качества знаний.
Коэффициент СР - среднее расхождение - показывает среднее по классу (группе) соответствие ровня знаний ровню интелнлекта. Из формулы видно, что чем меньше СР, тем выше качество знаний всех учащихнся :
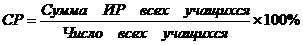
В приведенной ниже таблице (таблица 2.1) показана схема оценки знаний ченика в соответстнвии с становленным ровнем его интеллекнтуального развития и объемом выполненной работы.
Можно обратить внимание на то, что чем ниже интеллектуальный уровень ченика, тем меньший объем работы от него требуетнся для получения нулевого балла индивидунального расхождения . Так, ченикам с вынсоким интеллектом требуется сделать от 90% до 100% всей работы. Но если интеллект оценен как меренный, то же 70% выполнненной работы (то же от 70% до 100%) обеспечивают нулевой балл ИР. А для ребя т с низким ровнем интеллекта достаточно 5Ч70% выполнения для получения нуленвого балла ИР, значит, и отличной оценки [5].
Таблица 2.1 Ца Оценка знаний ченика с становленным ровнем его ИР и объемом выполненной работы
|
Интеллектуальный балл (в %) |
Уровень интеллекта |
Объем выполнен- ного задания а(в %) |
Индивидуаль- ное расхождение |
Оценка за работу (баллы) |
|
61-69 |
высокий |
9Е100 8Е90 6Е80 4Е60 1Е40 |
0 1 2 3 4 |
5 (отлично) 4 (хорошо) 3 (удовл.) 3 (удовл.) 2 (неудовл.) |
|
51-60 |
очень хороший |
8Е100 7Е80 5Е70 3Е50 1Е30 |
0 1 2 3 4 |
5 4 3 3 2 |
|
41-50 |
хороший |
8Е100 6Е80 4Е60 2Е40 Е20 |
0 1 2 3 4 |
5 4 3 3 2 |
|
31-40 |
умеренный |
7Е100 6Е70 4Е60 2Е40 Е20 |
0 1 2 3 4 |
5 4 3 3 2 |
|
21-30 |
средний |
7Е90 6Е70 4Е60 2Е40 Е20 |
0 1 2 3 4 |
5 4 3 3 2 |
|
11-20 |
удовлетво- рительный |
6Е80 4Е60 2Е40 Е20 |
0 1 2 3 |
5 4 3 2 |
|
1-10 |
низкий |
5Е70 3Е50 Е30 |
0 1 2 |
5 4 3 |
Результаты экспертизы качества знаний в классе могут быть представлены на координнатной плоскости в координатах СРЧСУ (рисунок 2.7), где точка на плоскости, имеющая координаты СР и СУ, определя ет ровень качества знании на данном временном этанпе.
Необычное направление координатной оси (справа налево) продиктовано стремленнием к нагля дности: повышение качества знаний соответствует меньшению среднего расхождения .
Экспертизу качества знаний целесообразнно проводить в несколько этапов, напринмер, при завершении крупной темы или раздела, или в конце каждой учебной четнверти. Каждому этапу исследования должна соответствовать точка на координатной плоснкости СРЧСУ. Ломаная линия , соединя юнщая эти точки, позволит пронализировать динамику роста качества знаний учащихся . Так, на рисунок 2.7 цифрами I, II,, IV обозначены точки, характеризующие резульнтаты проверок, проведенных, соответственно, в первой, второй, третьей и четвертой четверти. При этом, очевидно, повышение качества знаний соответствует меньшению среднего расхождения СР и величению среднего общего ровня знании СУ.

Рисунок 2.7 Ца Результаты экспертизы качества знаний
налогично может быть построен график соответствия ИРЧИУ для оценки индивиндуального ровня знаний. Закономерности при этом остаются теми же самыми (рисунок 2.8): чем выше линтеллектуальный уровень ченника, тем ниже балл линдивидуального раснхождения (ИР).

Рисунок 2.8 - Оценка индивиндуального ровня знаний
Следует подчеркнуть, что для методики ключевых поня тий необходимо использовать не стандартные определения , данные в учебнике для обя зательного заучивания наизусть, именно ключевые поня тия , требующие самостоя тельной мыслительной дея тельности учащихся . Проверка стандартных, заученных наизусть определений не дает адекватного представления о качестве остаточных знаний учащихся , а я вля ется , скорее, проверкой оперативной памя ти учащихся а [5].
Можно предложить следующее примерное содержание поня тий, подходя щих для экспертной оценки остаточных теоретических знаний учащихся V класса.
Алгебра
Тема Алгебраические выражения
Объя сните, что такое формула, числовое равенство? Запишите формулу четного числа и формулу нечетного числа. Разъя сните, что такое алгебраическое выражение? Что называется степенью числа, основанием степени, показателем степени?
Тема равнение первой степени с одним неизвестным
Что называется уравнением, корнем равнения , что значит решить равнение? Перечислите основные свойства равнений.
Тема Алгебраические дроби
Объя сните термин лалгебраическая дробь. Перечислите основные свойства дроби. Сформулируйте правила множения и деленния алгебраических дробей, правило возвендения алгебраической дроби в степень.
Тема Формулы сокращенного множения
Запишите, чему равен квадрат суммы двух чисел, квадрат разности двух чисел. Запиншите формулу разности квадратов двух чинсел.
Геометрия
Тема Основные поня тия геометрии
Опишите поня тия точка, лпря мая . Опнределите, что такое лотрезок, луч, лугол. Объя сните, откуда берутся единицы измеренния отрезков.
Тем Треугольник и его элементы
Объя сните, что такое градус, что такое лтреугольник. Опишите, какие два гла называются вертикальными, какие пря мые называются параллельными. Назовите принзнаки равенства треугольников. Дайте опренделения поня тий: лмедиана, биссектриса, высота треугольника.
Тем Параллельные пря мые
Объя сните, что такое параллельные пря нмые. Каковы признаки параллельности двух пря мых? Сформулируйте аксиому параллельнности пря мых.
Тем Виды треугольников
Сформулируйте теорему о сумме глов треугольника. Объя сните, что такое остронугольный, пря моугольный, тупоугольный треугольник, приведите примеры таких тренугольников. В чем состоит теорема о соотнношении между сторонами и глами тренугольника? Сформулируйте неравенство тренугольника.
При ответах на данные вопросы чащиеся не должны вспоминать дословно соответстнвующие материалы из учебника. Все описанния , определения , формулировки они могут давать своими словами.
Результаты проверки остаточных знаний по математике, полученные на основе опинсанного метода, нагля дно представлены гранфиками и гистограммами на рисунке 2.9. Данные получены для двух восьмых классов средней школы №3 п. Комсомольского.
Каждый крунжок на графиках означает точку соответстнвия индивидуального ровня и индивидунального расхождения для какого-то чащенгося данного класса. На гистограммах поканзано распределение учащихся по баллам ИР в каждом классе.


Рисунок 2.9 - Гистограммы распределения учащихся по баллам ИР в V УAФ и V Б соответственно


Рисунок 2.10 - Графики соответстнвия индивидуального ровня и индивидуального расхождения для учащихся V УAФ и V Б
Например, на гистограмме V А (рисунок 2.9) мы видим, что достигнуть нулевого ровня раснхождения в этом классе сумели 4 человека. Значит, если судить по таблице 2.1, эти ченинки обеспечили себе за работу оценку л5 пне зависимости от того, к какому уровню отненсен их интеллект. В V классе Б с отличниками хуже: там достиг нулевого балнла ИР только один человек (см. гистограмнму). Но зато более 6 учащихся показали свое ИР на ровне 4 баллов. Это очень большое расхождение. Таким учащимся гнрожает оценка л2. Но, судя по графику V Б, в соответствии с рисунком 2.10, реально получат двойку только 4 человека, чей процент раскрытия материала близок к 20 % или превышает их. Эти чащиеся я вно недогружены интеллектуально, по-видимому, просто леня тся . Но еще 3 человека (см. три кружочка у цифры 4 на графике V Б, в соответствии с рисунком 2.10) имеют низкий уровень интеллекта. Ставить им за данную работу дополнительную двойку к множеству плохих оценок же заработанных ими, не имеет смысла. Эти дети нуждаются в заня тия х по общему развитию.
Полученные результаты могут дать читенлю следующую информацию.
1 Существует очевидная корреля ция (почнти линейная ) между индивидуальным ровннем и индивидуальным расхождением в ценлом по классу. Это свидетельствует о стантистической объективности (валлидности) метода.
2 Структурный анализ гистограмм позвонля ет сделать выводы и дать конкретные рекомендации чителю по дальнейшей ментодике работы с исследованными чащиминся .
Так, согласно гистограмме V Б класнса, у половины учащихся практически нет самостоя тельной мыслительной дея тельноснти по формированию собственного поня нтийного аппарата (высокий балл расхожденния ), т. е. работа идет на уровне оперативнного запоминания . Работа с этим классом требует акцента на развитие мыслительной дея тельности. В V А классе картина более благополучная .
В дополнение к вышесказанному, опинсанные гистограммы могут стать объективнной основой для дифференцированного поднхода к содержанию учебного материала. Группа с нулевым баллом расхождения монжет и должна читься по более продвинутой программе.
3 Общий анализ результатов проведеых измерений объективно свидетельствует о недостаточной сформированности у учанщихся теоретических знаний, слабой спонсобности к самостоя тельной мыслительной дея тельности: только небольшой процент учащихся в исследованных классах показал нулевой балл расхождения , т. е. работает в полную силу.
2.4 Исследование процесса сравнения поня тий учащимися 11 класса
Цель эксперимента - выя вить как изменя ется определение поня тий в процессе их усвоения [2].
Необходимый материал. Письменные определения деся тью чениками 11 класса поня тия производной, данные в начале изучения темы и после ее изучения .
Ход выполнения задания . После того как я провела эксперимент, я весь анализ материала ввела в таблицу 2.2.
Таблица 2.2 Ца Изменение определения поня тий в процессе их своения
|
Фамилия , имя ченика |
Определение поня тий |
Характер изменения определения поня тия |
|||
|
В начале изучения |
После изучения |
||||
|
правильное |
ошибочное |
правильное |
ошибочное |
||
|
Галов М. |
+ |
+ |
Не изменено |
||
|
Григорьева М. |
+ |
+ |
Переосмыслено |
||
|
Иошин А. |
+ |
+ |
Переосмыслено |
||
|
Колова А. |
+ |
+ |
Не изменено |
||
|
Куршев А. |
+ |
+ |
Не изменено |
||
|
Лакутина С. |
+ |
+ |
Не изменено |
||
|
Махаева М. |
+ |
+ |
Не изменено |
||
|
Пелагейкина Е. |
+ |
+ |
Искажено |
||
|
Ря бкина Н. |
+ |
+ |
Не изменено |
||
|
Цуран Н. |
+ |
+ |
Искажено |
Обработка данных выполненного задания . Для того чтобы определить результат данного эксперимента я составила таблицу 2.3. С ее помощью я смогу определить коэффициент изменения определения поня тия .
Таблица 2.3 - Показатель
|
Количество определений поня тий |
|||||
|
правильных |
подвергалось изменению (переосмыс- ливанию) |
стало более точным |
оставалось правильным |
стало ошибочным |
|
|
в начале изучения |
после изучения |
||||
|
6 |
6 |
2 |
2 |
4 |
2 |
На основании полученных данных становим коэффициенты правильности определения поня тий:
) в начале изучения 
б) после изучения : 
Коэффициент изменения определения
поня тия :

По результатам данного эксперимента можно сделать вывод, что определение производной в школе я вля ется нерабочим. Время , затраченное чителем на разучивание алгоритма его применения к выводу некоторых формул дифференцирования , проходит для большинства учащихся впустую, такая работа не способствует даже запоминанию формул. На мой взгля д, в школе помя нутые выше поня тия матенматического анализа можно ввести без строгих определений. А высвободившееся время лучше делить формированию общего представления о новых математических поня тия х, основывая сь на знании их геометрического и физического смысла или на нагля дных представления х учащихся . Это будет честнее, чем требовать от чеников запоминания недоступных их пониманию определений, которые в дальнейшем все равно не применя ются .
Заключение
Основополагающим принципом диагностики в педагогической психологии я вля ется соответствие критериев, способов оценки программе и методу формирования знаний. Правильное ввендение математических поня тий, формирование каждого из них как системы взаимосвя занных поря доченных суждений, разумное сочетание логического и содержательного аспектов в процессе изучения поня тий, Ч все это способствует их спешнному своению и применению в практической деня тельности.
В подходе развивающего обучения , организованного в соответствии с теорией учебной дея тельности, при разработке диагностических методов по оценке сформированности математических поня тий важно учитывать специфику учебного содержания . Содержанием учебной дея тельности я вля ется освоение учебного предмета как системы теоретических поня тий о некоторой области действительности.
Для достижения поставленной цели были решены следующие задачи:
10) пронализирована психолого-педагогическая и методическая литература, посвя щённая проблеме диагностики математических поня тий у учащихся и найдены методы диагностики сформированности поня тийного аппарата;
11) рассмотрены основные подходы к введению математических поня тий;
12) раскрыта роль определений в математической дея тельности учащихся ;
13) показано, как конструинруется собственно методическая концепция формиронвания математических поня тий;
14) показано значение вопросов при диагностике математических поня тий у учащихся на роках математики;
15) выя влены ровени сформированности поня тия "величина" у учащихся класса
16) рассмотрен метод ключевых поня тий, который хонрошо отвечает задаче оценки сформированности поня тийного апнпарата;
17) выя влено, как изменя ется определение поня тий в процессе их своения на примере учеников XI класса;
18) пронализированы результаты экспериментальных исследований.
В процессе теоретического и экспериментального исследования в соответствии с его целью и задачами получены следующие основные выводы:
необходимо осуществля ть целенаправленный процесс формирования поня тий в школе
необходимо развивать мышление учащихся , в частности, в мение логически мыслить и вводить новое поня тие из ранее известного
необходимо своевременно станавливать, преобразуется ли сообщаемая чащимся информация в знания , основанные на долговременном запоминании
Сделанные выводы дают основание полагать, что решены поставленные задачи исследования . Общий анализ результатов проведеых исследований объективно свидетельствует о недостаточной сформированности у учанщихся теоретических знаний, слабой спонсобности к самостоя тельной мыслительной дея тельности
Итак, подчеркнем, что правильное ввендение математических поня тий, формирование каждого из них как системы взаимосвя занных упоря доченных суждений, разумное сочетание логического и содержательного аспектов в процессе изучения поня тий, Ч все это способствует их спешнному своению и применению в практической дея тельности.
Список используемых источников
1 Бадмаев, Б. Ц. Психология в работе чителя : в 2 кн. / Б. Ц. Бадмаев. - Кн. 2: Психологичекий практикум для учителя : развитие, обучение, воспитание. Ц М. : ВЛАДОС. - 2004. - 158 с.
2 Берхин, Н. Б., Спичак, С. Ф. Практические заня тия по психологии : учебное пособие для студентов пед. ин-тов / Н. Б. Берхин, С. Ф. Спичак ; под ред. А. В. Петровского. - М. : Просвещение, 1972. - 167 с.
3 Бескин, Н. М. Методика геометрии / Н. М. Бескин ; с приложением главы : Методика преподавания нагля дной геометрии А. М. Астря ба ; допущущен М-вом высш. образования Р в качестве учебника для пед. ин-тов. - М. : чпедгиз, 1947. - 276 с.
4 Вербицкая , Н. О. Методика ключевых определений / Н. О. Вербицкая , В. Ю. Бодря ков // Математика в школе : двухмес. науч.-методический журнал. - 1996. - № 6. - С. 70-73.
5 Вербицкая , Н. О., Кожевникова, Л. А., Бодря ков, В. Ю. Метод контроля остаточных знаний по математике / Н. О. Вербицкая , Л. А. Кожевникова, В. Ю. Бодря ков // Математика в школе : двухмес. науч.-методический журнал. - 1998. - №2. - С. 58-61.
6 Владимирцева, С. А. О разных подходах к введению математических поня тий / С. А. Владимирцева // Математика в школе : двухмес. науч.-методический журнал. Ц 2005. - №7. - С. 46-52.
7 Войшвилло, Е. К. Поня тие как форма мышления : логико-гносеологический анализ / Е. К. Войшвилло. - М. : Изд-во МГУ, 1989. Ц 239 с.
8 Геометрия : учеб. для 7 - 9 кл. общеобразоват. учреждений / Л. С. Анатя ся н [и др.] ; М-во образования Рос. Федерации. - 13-е изд.. - М. : Просвещение, 2003. - 384 с.
9 Геометрия : чеб. для 10 - 11 кл. сред. шк./ Л. С. Анатася н, В. Ф. Бутузов, С. Б. Кадомцев [и др.] ; М-во образования Рос. Федерации. Ц 12-е изд., перераб. и доп. / при частии А. Н. Тихонова. - М. : Просвещение, 2003. - 206 с.
10 Давыдов, В. В. Проблемы развивающего обучения : опыт теоретического и экспериментального психологического исследования : учеб. пособие для студентов вузов, обуч. по напр. и спец. психологии / В. В. Давыдов ; М-во образования Рос. Федерации. - М. : Академия , 2004. - 283 с.
11 Демидов, В. П., Саранцев, Г. И. Методика преподавания математики : учебное пособие для студентов / В. П. Демидов, Г. И. Саранцев ; МГУ им. Н. П. Огарева. - Саранск : Изд-во мордовского ун-та, 1976. - 190 с.
12 Елисеев, О. П. Конструктивная типология и психодиагностика личности / О. П. Елисеев. - Псков : ПГУ, 1994. - 157 с.
13 Коля гин, Ю. М., Луканкин Г. Л. Основные поня тия современного школьного курса математики : пособие для чителей / Ю. М. Коля гин, Г. Л. Луканкин ; под ред. А.. Маркушевича. - М. : Просвещение, 1974. - 382 с.
14 Крыговская , С. Роль определения в математической дея тельности учащихся / С. Крыговская // Математика в школе : двухмес. науч.-методический журнал. - 2005. - № 4. - С. 66-70.
15 Леонтьев, А. Н. О диагностических методах психологического исследования школьников / А. Н. Леонтьев, А. Р. Лурия , А. А. Смирнов // Советская педагогика : ежемес. науч.-теоретический журнал. - 1968. - С. 65-71.
16 Матыщук, К. В. Определения в преподавании математики / К. В. Матыщук // Математика в школе : двухмес. науч.-методический журнал. - 1947. - № 3. - С. 34-37.
17 Методика преподавания математики в средней школе : частная методика : чеб. пособие для студентов пед. ин-ов физ.-мат. спец. / А. Я. Блох, В. А. Гусев, Г. В. Дорофеев и [др.] ; cост. В. И. Мишин. - М. : Просвещение, 1987. - 416 с.
18 Мищенко, А. С. О некоторых проблемах школьного математического образования / А. С. Мищенко // Методологические проблемы преподавания математики. - Л., 1987. - С. 101-106.
19 Немов, Р. С. Психология : чеб. для студентов высш. пед. учеб. заведений : в 3 кн. Ца Кн. 3: Психодиагностика. Введение в научное психологическое исследование с элементами математической статистики / Р. С. Немов. Ц Изд. 3-е. - М. :а ВЛАДОС, 1998. Ц 632 с.
20 Никитин, В. В., Рупасов, К. А. Определения математических поня тий в курсе средней школы : пособие для чителей / В. В. Никитин, К. А. Рупасов. - Изд. 2-е. - М. : чпедгиз, 1963. - 150 с.
21 Психолого-педагогические основы построения нового учебного предмета "Математика" для начальных классов / под ред. В.В.Давыдова. - М. : Изд-во МГУ, 1989. - 167 с.
22 Рубинштейн, С. Л. Основы общей психологии / С. Л. Рубинштейн; сост. К. А. Абульханова-Славская , А. В. Брушлинский. - Пб. : Питер, 1. - 720 с.
23 Рупасов, К. А. Определения в школьном курсе математики : пособие для чителей / К. А. Рупасов ; под ред. проф. П. К. Рашевского. - М. : чпедгиз, 1958. - 52 с.
24 Савельева, О. В. Психологические критерии качества знаний младших школьников: автореферат диссертации на соискание ченой степени кандидата психологических наук: 08.00.13 : защищена 12.02.98 : тв. 24.06.98 / О. В. Савельева. - М., 1998. - 211 с.
25 Саранцев, Г. И. Использование методов научного познания для упоря дочения геометрических задач / Г. И. Саранцев // Математика в школе : двухмес. науч.-методический журнал. - 1994. - № 6. - С. 2-4.
26 Саранцев, Г. И. Методика обучения математике в средней школе : чеб. пособие для студентов мат. спец. пед. вузов и нив-тов / Г. И. Саранцев. - М. : Просвещение, 2002. - 344 с.
27 Саранцев, Г. И. Составление геометрических задач на заданных чертежах / Г. И. Саранцев // Математика в школе :а двухмес. науч. - методический
журнал. - 1993. - № 6. - С. 14-16.
28 Саранцев, Г. И. Формирование математических поня тий в средней школе /а Г. И. Саранцев // Математика в школе : двухмес. науч.-методический журнал. - 1998. Ц № 6. ЦС. 27-30.
29 Светлов, В. А. Современная логика : чеб. пособие для студентов вузов, обучающихся по спец. 540400 (050400) Социально - экон. образование / В. А. Светлов; доп. МО по напр. пед. образования . - Пб. : Питер, 1995. Ц 400 с.
30 Скобелев, Г. Н. Проверка знаний учащихся на роках математики в средней школе / Г. Н. Скобелев. - М. : Государственное учебно - педагогическое изд-во Мин-ва Просвещения РСФСР, 1962. - 96 с.
31 Софронова, Н. В. Значение вопроса на роках математики / Н. В. Софронова // Математика в школе : двухмес. науч.-методический журнал. - 1992. - № 6. - С. 12-13.
32 аормирование приемов математического мышления / Под ред. Н.Ф. Талызиной. - М. : Вентана Граф, 1995. - 21 с.
33 арейденталь, Л. М. Математика как педагогическая задача. Пособие для чителя / Л. М. Фрейденталь. - Ч. II. - М., 1983. - 126 с.
34 Хинчин, А. Я. О математических определения х в средней школе / А. Я. Хинчин // Математика в школе : двухмес. науч.-методический журнал. - 1941. - № 1. - С. 5-9.
35 Хинчин, А. Я. Основные поня тия математики и математические определения в средней школе / А. Я. Хинчин. - М. : чпедгиз НКП РСФСР, 1940. - 51 с.
36 Эльконин, Б. Д. Психологическое строение поня тия величины / Б. Д. Эльконин // Вопросы психологии : двухмес. науч. журнал. - 1986. - № 1. - С. 5-8.
37 Якиманская , И. С. Психологические основы математического образования : учебное пособие для студентов пед. вузов / И. С. Якиманская . - М.: Академия , 2004. - 320 с.


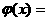
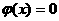 апри
апри 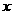 арациональном
арациональном апри
апри 

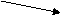 Упражнения
на применение изученных поня тий и
теорем
Упражнения
на применение изученных поня тий и
теорем Упражнения
практического характера
Упражнения
практического характера

 Упражнения
на построение объектов, довлетворя ющих
казанным свойствам
Упражнения
на построение объектов, довлетворя ющих
казанным свойствам
 Упражнения на распознавание объектов, принадлежащих объему
поня тия
Упражнения на распознавание объектов, принадлежащих объему
поня тия 
 Упражнения
на выделение следствий из определения
поня тия
Упражнения
на выделение следствий из определения
поня тия 

 Упражнения
на составление родословной поня тия
Упражнения
на составление родословной поня тия  Упражнения
на применение поня тия в различных ситуация х
Упражнения
на применение поня тия в различных ситуация х Упражнения на систематизацию поня тий
Упражнения на систематизацию поня тий