Ое обеспечение автоматизированных систем математического факультета кбгу, старший научный сотрудник нии информатики и проблем регионального управления кбнц ран
| Вид материала | Документы |
- А. Ж. Макашева викторов И. С., главный научный сотрудник нии проблем укрепления закон, 169.47kb.
- «горные экосистемы и их компоненты» посвящается памяти основателя иэгт кбнц ран, 98.22kb.
- Номер: за 1994 год, 300.09kb.
- 3 августа 1910 года, 146.02kb.
- -, 252.58kb.
- “Четвертая часть всех домохозяйств, 328.98kb.
- Качество жизни в информационном обществе, 629.78kb.
- О сотрудничестве по уголовным делам, 979.88kb.
- Самойленко Павел Романович, 52.67kb.
- Нп «сибирская ассоциация консультантов», 65.39kb.
Распределение баллов зависит от процента правильных ответов и может лежать в различных границах, например: "отлично" – более 95% правильных ответов, "хорошо" – 80–94%, "удовлетворительно" – 60–79%, "неудовлетворительно" – менее 60%. К каждой системе такого распределения баллов могут быть предъявлены замечания.
Для измерения "уровеня образованности" ("уровня знаний") лучше использовать логарифмическую шкалу, так называемые "логиты". Поясним эту шкалу.
Очень трудные задания снижают учебную мотивацию многих учащихся, как и очень легкие. Поэтому используется шкала, которую ввел датский математик Г. Раш (Г. Раск, G. Rasch), шкала "логитов". По Рашу определены два логита:
- "логит уровня знаний" – натуральный логарифм отношения доли правильных ответов испытуемого на все задания теста, к доле неправильных ответов;
- "логит уровня трудности задания" – натуральный логарифм отношения доли неправильных ответов на задание теста к доле правильных ответов на это задание по множеству испытуемых.
Необходимо на всех этапах тестирования учитывать, что первичные баллы – необъективны (в математико-статистическом смысле).
Результаты тестирования могут свидетельствовать иногда и о том, что есть интеллектуально развитые обучаемые, показывающие плохие результаты тестирования, как и слабые обучаемые с так называемым критическим складом ума и хорошей моторной памятью, показывающие неплохие результаты.
Необходимо учитывать дидактическую ограниченность проверки на совпадение с эталоном ответа, особенно, при компьютерной проверке знаний и умений.
Тестирование обычно завершается математико-статистической обработкой данных тестирования.
Рассмотрим вначале некоторые необходимые понятия математической статистики и теории вероятностей.
Пусть задан некоторый статистический ряд из элементов
 . Если эти элементы могут принимать все мыслимые допустимые значения, а объект с этими характеристиками рассматривается как единый (как система), то такую совокупность называют генеральной совокупностью; часто при этом предполагается, что она является конечной и упорядоченной по возрастанию:
. Если эти элементы могут принимать все мыслимые допустимые значения, а объект с этими характеристиками рассматривается как единый (как система), то такую совокупность называют генеральной совокупностью; часто при этом предполагается, что она является конечной и упорядоченной по возрастанию:  .
.Любое непустое подмножество генеральной совокупности называется выборкой. Если выборка осуществлена случайным образом, то она называется случайной выборкой.
Средняя величина генеральной совокупности в целом называется общей средней. Она отражает общие черты всей совокупности. Средняя величина для отдельной выборки называется средней по выборке или выборочной средней. Она отражает общие черты группы.
Существуют различные меры средних величин. Чаще используется средняя арифметическая характеристика:
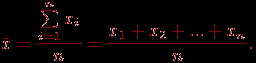
Она называется также выборочной средней или эмпирической средней.
Средняя гармоническая величина, как и средняя арифметическая, может быть простой и взвешенной. Если все веса равны между собой, то можно использовать среднюю гармоническую в виде:
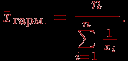
Средняя квадратичная взвешенная величина вычисляется по формуле:
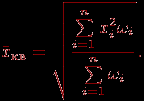
Если веса
 , для всех
, для всех 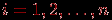 , то получаем просто среднее квадратичное. Эти величины характеризуют "концентрацию" данных выборки около среднего (или другой характерной тенденции).
, то получаем просто среднее квадратичное. Эти величины характеризуют "концентрацию" данных выборки около среднего (или другой характерной тенденции).К средним величинам, которые характеризуют структурные изменения, относятся мода и медиана. Они определяются лишь структурой распределения.
Мода – наиболее часто встречающееся значение признака у элементов данной совокупности. Она соответствует определенному значению признака.
Медиана - значение признака, которое делит элементы ранжированной выборки на две равные части. Это середина ранжированного ряда.
Исход – одно из возможных заключений о рассматриваемом процессе.
Выборочное пространство – множество всех исходов.
Событие – любое подмножество выборочного пространства. Пустое событие обозначают, как и в теории множеств, символом
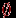 . Событием можно считать и всё выборочное пространство (универсальное событие).
. Событием можно считать и всё выборочное пространство (универсальное событие).Испытание – проверка всевозможных исходов события.
Два испытания независимы, если любое событие, определённое на основе только одного из них, не зависит от любого события, определённого на основе другого.
Так как событие – это множество, то для них должны быть выполнимы основные операции с множествами: объединение, пересечение и дополнение.
Два события
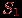 и
и 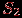 несовместимы, если
несовместимы, если 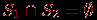 .
.События
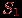 и
и 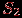 образуют полную группу, если
образуют полную группу, если 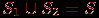 (всему выборочному пространству).
(всему выборочному пространству).События
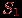 и
и 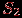 – противоположны, если они несовместимы и образуют полную группу.
– противоположны, если они несовместимы и образуют полную группу.Пусть
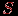 – событие,
– событие, 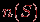 – число случаев (исходов), в которых произошло событие
– число случаев (исходов), в которых произошло событие 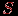 из проведенной серии
из проведенной серии 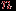 испытаний (в выборочном пространстве). Тогда
испытаний (в выборочном пространстве). Тогда 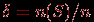 – относительная частота события
– относительная частота события 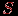 .
.При больших
 ,
,  . Эта предельная частота называется вероятностью события
. Эта предельная частота называется вероятностью события 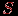 и обозначается как
и обозначается как 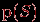 или просто
или просто 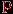 . Всегда
. Всегда 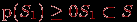 , а
, а 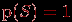 .
. Важно заметить, что указанный предел не может быть вычислен как предел функции (последовательности), так как её просто нет.
Изложим ряд наиболее часто решаемых и наиболее простых (специально упрощенных) задач, которые часто встречаются при подготовке к тестированию и математической обработке результатов тестирования, а также алгоритмы их решения. При этом мы не будем сильно вдаваться в обоснование используемых математических фактов, используя их, как принято в прикладных задачах, в качестве инструментария (это осуществляется и с целью расширить читательский состав).
Задача 1.
Пусть теперь даны результаты тестирования группы, состоящей из
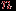 испытуемых для заданного теста из
испытуемых для заданного теста из 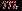 различных знаний. Обычно эти данные представляются в виде некоторой матрицы
различных знаний. Обычно эти данные представляются в виде некоторой матрицы 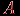 баллов (типа "тестируемый – задание") размерности
баллов (типа "тестируемый – задание") размерности 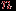 на
на 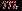 :
: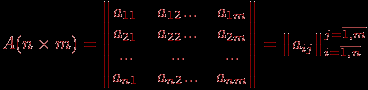
Элемент
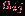 матрицы
матрицы 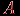 представляет собой результат выполнения
представляет собой результат выполнения 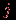 -го задания для
-го задания для 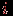 -го тестируемого.
-го тестируемого. Необходимо на основе имеющихся результатов
 тестирования для каждого из
тестирования для каждого из 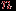 тестированных, вычислить основные статистические показатели тестирования (оценить "сырые" результаты) для выбранной случайным образом группы тестированных.
тестированных, вычислить основные статистические показатели тестирования (оценить "сырые" результаты) для выбранной случайным образом группы тестированных.Алгоритм решения этой задачи состоит из следующих этапов.
- Упорядочиваем ряд по возрастанию (находим генеральную совокупность):
 .
.
- Выбираем интересующее нас подмножество тестированных (выборку).
- Находим среднее арифметическое по выборке
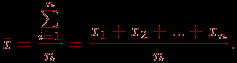
- Находим среднюю гармоническую величину выборки:
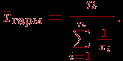
- Находим величины, характеризующие структурные изменения, например, моду и медиану. Для данных, имеющих "хорошее поведение", медиана всегда лежит в промежутке между средним арифметическим и модой. Эти величины выстраиваются по возрастанию следующим образом (напомним про упорядоченность по возрастанию выборки, предполагаемую нами далее для любого статистического ряда): среднее, медиана, мода, или же в обратном порядке. Прямой или обратный порядок их расположения можно определить, вычислив так называемый коэффициент асимметрии:
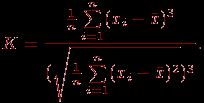
Этот коэффициент отражает относительную изменчивость данных.
- Находим меры рассеяния, разброса или вариации, показывающие, как остальные элементы совокупности (выборки) группируются около средних величин. Например,
- размах
- размах

- среднее абсолютное отклонение
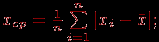
- среднеквадратичное отклонение
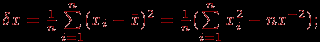
- дисперсия
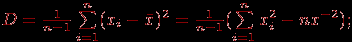
- стандартное отклонение:
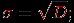
- коэффициент вариации:
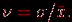
- Конец алгоритма.
| Задача 2. Даны результаты тестирования для каждого из n тестированных и теста длины 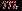 в виде матрицы в виде матрицы 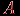 , а также вектор эталонных ответов , а также вектор эталонных ответов 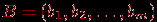 , где , где 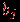 – эталонный ответ на задание номер – эталонный ответ на задание номер 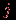 . Необходимо определить "вес" (меру сложности) конкретного задания теста. . Необходимо определить "вес" (меру сложности) конкретного задания теста.Простейший алгоритм решения этой задачи состоит из следующих этапов.
Задача 3. Даны результаты тестирования для каждого из 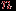 тестированных и теста длины тестированных и теста длины 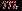 в виде матрицы в виде матрицы 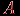 , а также вектор эталонных ответов , а также вектор эталонных ответов 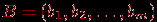 , где , где 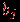 – эталонный ответ на задание номер – эталонный ответ на задание номер 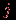 . Необходимо оценить валидность каждого задания теста. . Необходимо оценить валидность каждого задания теста.Простейший алгоритм решения этой задачи состоит из следующих этапов.
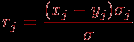
Задача 4. Даны результаты нормативно-ориентированного тестирования для каждого из 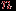 тестированных и теста длины тестированных и теста длины 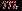 в виде матрицы в виде матрицы 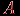 , а также вектор эталонных ответов , а также вектор эталонных ответов 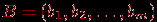 , где , где 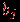 – эталонный ответ на задание номер – эталонный ответ на задание номер  . Необходимо оценить надежность теста (степень устойчивости результатов тестирования каждого испытуемого, если тестирование было проведено в совершенно одинаковых условиях). . Необходимо оценить надежность теста (степень устойчивости результатов тестирования каждого испытуемого, если тестирование было проведено в совершенно одинаковых условиях).Для вычисления надежности нормативно-ориентированного теста используем коэффициент корреляции между результатами двух параллельных тестов. Сравнивая коэффициенты корреляции, делаем заключение о надежности (внутренней) теста. Если две половины теста коррелированны, то и тест надёжен; в противном случае – не надёжен (или необходимо применить другой, более тонкий математический аппарат исследования надежности). Простейший алгоритм решения этой задачи состоит из следующих этапов.
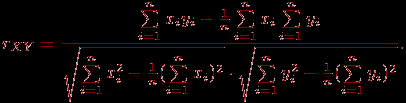
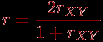
Задача 5. Необходимо на основе имеющихся результатов тестирования (матрица  ) получить для каждого из ) получить для каждого из 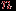 тестированных интегральный (обобщенный) показатель выполнения теста длины тестированных интегральный (обобщенный) показатель выполнения теста длины 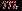 , а затем по вычисленным значениям этого интегрального показателя разбить всех тестированных на заданное количество , а затем по вычисленным значениям этого интегрального показателя разбить всех тестированных на заданное количество 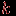 групп (задача классификации). групп (задача классификации).Алгоритм решения этой задачи состоит из следующих этапов.
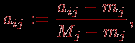 где 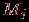 , , 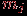 – наибольшее и наименьшее значения элементов – наибольшее и наименьшее значения элементов 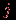 -го столбца и применяем преобразование вида -го столбца и применяем преобразование вида 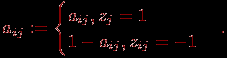
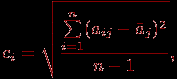 где 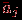 – среднее арифметическое элементов – среднее арифметическое элементов 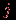 -го столбца. -го столбца.
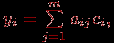 где  – значение интегрального показателя для – значение интегрального показателя для 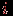 -го обучаемого -го обучаемого 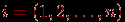 , – весовой коэффициент , – весовой коэффициент 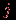 -го задания в тесте или в банке всех заданий, -го задания в тесте или в банке всех заданий, 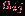 – элемент матрицы – элемент матрицы 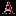 или его преобразованное (нормированное, например, по отношению к максимальному элементу или к норме матрицы). или его преобразованное (нормированное, например, по отношению к максимальному элементу или к норме матрицы).
Задача 6. Дана интегральная норма 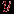 тестовых результатов. Необходимо разбить группу тестированных на несколько групп по их интегральным показателям (по отношению их к норме). тестовых результатов. Необходимо разбить группу тестированных на несколько групп по их интегральным показателям (по отношению их к норме).Приведем простейший алгоритм решения этой задачи. Первый алгоритм решения этой задачи состоит из следующих этапов.
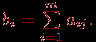
Задача 7. Необходимо отсеять первичные ("сырые") результаты в группах, т.е. по данным  (процент выполнения, валидность и т.д.) выяснить задания (тесты, результаты), которые не согласуются с общей картиной тестирования. (процент выполнения, валидность и т.д.) выяснить задания (тесты, результаты), которые не согласуются с общей картиной тестирования.Алгоритм решения задачи состоит из следующих этапов.

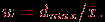
 |
 |
| |
| Случайная величина – числовая переменная (числовая функция), определённая на выборочном пространстве (или приписываемая некоторому выборочному пространству) таким образом, что каждой точке выборочного пространства соответствует одно и только одно значение этой переменной. Если множество всех теоретически возможных значений величины 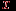 конечно или счётно, то её называют дискретной случайной величиной. конечно или счётно, то её называют дискретной случайной величиной.Функция 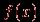 , которая для каждого возможного значения , которая для каждого возможного значения 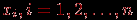 (или (или  ) дискретной случайной величины ) дискретной случайной величины 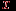 равна вероятности равна вероятности 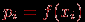 появления этого значения, задаёт распределение вероятностей случайной величины. Таким образом, эта функция задаёт множество значений, которые может принимать случайная величина, вместе с соответствующими им вероятностями. появления этого значения, задаёт распределение вероятностей случайной величины. Таким образом, эта функция задаёт множество значений, которые может принимать случайная величина, вместе с соответствующими им вероятностями.Величину 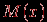 , определяемую формулой , определяемую формулой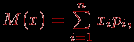 называют математическим ожиданием дискретной случайной величины 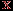 . .Величину, определяемую формулой 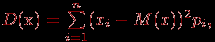 называют дисперсией этой случайной величины. Математическое ожидание характеризует центр распределения (аналог среднего выборки), а дисперсия – степень рассеяния значений случайной величины вокруг центра (аналог рассеяния в выборке). Эти формулы дают возможность получить оценку математического ожидания и дисперсии на основе опытных данных. Если случайная величина распределена непрерывно и задана некоторой функцией распределения 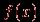 , то , то 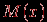 и и 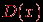 определяются по соответствующим формулам (для ограниченного и бесконечного множества изменения случайной величины): определяются по соответствующим формулам (для ограниченного и бесконечного множества изменения случайной величины): 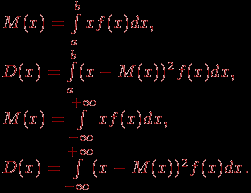 Основная цель статистических расчетов, как правило, состоит в том, чтобы по характеристикам выборки получить достоверную информацию о свойствах исходных генеральных совокупностей. Рассмотрим теперь укрупнено (не приводя, как выше, алгоритмы на уровне, достаточном для реализации, программирования) комплекс задач, который связан с обоснованием принятия гипотез тестирования. Есть процедуры, позволяющие отвергнуть проверяемую гипотезу как противоречащую имеющимся данным, либо убедиться в том, что гипотеза этим данным не противоречит. Располагая каким-то распределением данных тестирования, можно исследовать возможность описания этой совокупности каким-то типовым распределением, если тип распределения неизвестен, а затем найти неизвестный параметр распределения, а также эффективность описания. Наиболее часто рассматриваются гипотезы в основе которых лежат известные распределения: нормальное (Гаусса), 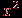 , Стьюдента и Фишера. Существуют различные процедуры проверки гипотезы о принадлежности заданного эмпирического распределения к некоторому теоретическому типу. , Стьюдента и Фишера. Существуют различные процедуры проверки гипотезы о принадлежности заданного эмпирического распределения к некоторому теоретическому типу.Рассмотрим нормальное распределение (распределение Гаусса). Это распределение – наиболее часто встречающееся непрерывное распределение (точнее было бы сказать, что это распределение, к которому "подгоняется" большинство изучаемых распределений). Такому закону или его различным модификациям подчиняются многие наборы случайных величин. Общий вид нормального распределения задаётся функцией: 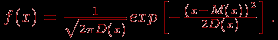 Часто используется стандартное нормальное распределение или распределение вероятностей нахождения (попадания) случайной величины в интервал 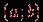 . Для вычисления значений такой функции используется интеграл (таблица значений этого, не берущегося в квадратурах, интеграла): . Для вычисления значений такой функции используется интеграл (таблица значений этого, не берущегося в квадратурах, интеграла):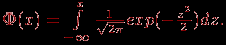 Необходимо на основе имеющихся результатов тестирования проверить гипотезу нормального распределения результатов тестирования, например, достижений (можно в качестве достижения принять среднее арифметическое по всем тестам) тестированных в зависимости от выборки. Самый простой, но математически менее надежный алгоритм – построения графика (эскиза) и его анализ. Процедура может быть следующей.
Оценку соответствия рассматриваемого распределения нормальному распределению можно осуществить также и по величине асиммет¬рии: 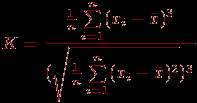 Если имеет место левая асимметрия (сдвиг влево), то это говорит о том, что в тесте были облегченные задания, на которые сумели правильно ответить подавляющее большинство испытуемых, а также были усложненные задания, с которыми не смогли справиться подавляющее большинство испытуемых. Если имеет место правая асимметрия (сдвиг вправо), то это говорит о том, что в тесте был очень низкий порог трудности для данного контингента испытуемых. Алгоритм проверки гипотезы о нормальном законе распределения с помощью коэффициента асимметрии может реализовываться следующими шагами.
Знание закона распределения баллов необходимо для выработки нормативной шкалы, которая позволит соотнести равные отрезки под кривой распределения равным количествам правильных ответов. Распределение можно получить следующей процедурой:
Необходимо искусственно приводить распределение первичных тестовых оценок к нормальному виду, так как она наиболее изучена (проста) в математической статистике и дает возможность описывать диагностические нормы в компактной форме. Обычно рассматриваются гистограммы распределения первичных тестовых оценок. Они позволяют выявлять лево- и правостороннюю асимметрию, положительный или отрицательный эксцесс и другие "ненормальности". Применение известных статистических программных пакетов позволяет автоматизировать подгонку требуемого преобразования первичных тестовых оценок к комбинациям различных базисных аналитических функций, что также позволяет стандартизировать тестовые оценки.  |
| |
 |

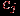 : знаменатель – количество тестированных, числитель – количество тестированных, давших правильные ответы на все задания.
: знаменатель – количество тестированных, числитель – количество тестированных, давших правильные ответы на все задания. 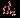 : знаменатель – количество всех тестированных, давших неправильный ответ на данное задание номер
: знаменатель – количество всех тестированных, давших неправильный ответ на данное задание номер 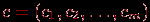 для заданного вектора
для заданного вектора 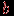 эталонных ответов.
эталонных ответов. 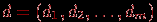 для заданного вектора
для заданного вектора  и стандартное отклонение
и стандартное отклонение 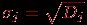 .
. 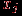 .
. 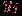 .
. 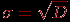 по всему тесту.
по всему тесту. 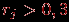 , то задание считаем валидным, иначе – не валидным (отметим, что с точки зрения критериальной валидности, задания, выполненные всеми или невыполненные никем, не являются валидными).
, то задание считаем валидным, иначе – не валидным (отметим, что с точки зрения критериальной валидности, задания, выполненные всеми или невыполненные никем, не являются валидными).  и
и  , например, по четным и нечетным номерам заданий. Этот метод называется методом расщепления теста. Таким образом, мы имеем данные по двум параллельным тестам
, например, по четным и нечетным номерам заданий. Этот метод называется методом расщепления теста. Таким образом, мы имеем данные по двум параллельным тестам  ,
,  , где
, где  всего теста по формуле (Спирмена-Брауна):
всего теста по формуле (Спирмена-Брауна): 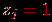 , а если свидетельствует об ухудшении – признак
, а если свидетельствует об ухудшении – признак  .
. 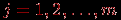 ) и для каждого испытуемого
) и для каждого испытуемого  и наибольшее
и наибольшее 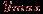 значения интегрального показателя (по всем тестированным). Отрезок
значения интегрального показателя (по всем тестированным). Отрезок 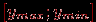 делим на заданное число
делим на заданное число 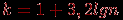 . Всех тестированных, для которых вычисленные значения интегрального показателя попадают в один и тот же интервал, отождествляем и относим к одному классу.
. Всех тестированных, для которых вычисленные значения интегрального показателя попадают в один и тот же интервал, отождествляем и относим к одному классу. 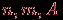 .
. 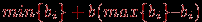 , группа 2 со средними баллами и группа 3 с низкими баллами (верхняя граница суммарного балла для попадающих в эту группу равна
, группа 2 со средними баллами и группа 3 с низкими баллами (верхняя граница суммарного балла для попадающих в эту группу равна 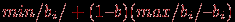 , где
, где 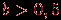 .
. 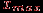 и наименьшее
и наименьшее  в группе.
в группе. 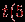 и
и 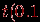 . Таблица Стьюдента имеется практически во всех справочниках по математической статистике.
. Таблица Стьюдента имеется практически во всех справочниках по математической статистике. 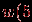 ,
, 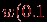 .
. 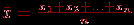 .
. 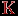 по вышеприведенной формуле.
по вышеприведенной формуле.  , где
, где 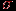 – среднеквадратичное отклонение; если же распределение не подчиняется нормальному закону, то либо изменяют тесты до тех пор пока не получим нормальное распределение, либо принудительно нормализуют распределение, либо используют шкалы, ориентированные на другие типы распределений.
– среднеквадратичное отклонение; если же распределение не подчиняется нормальному закону, то либо изменяют тесты до тех пор пока не получим нормальное распределение, либо принудительно нормализуют распределение, либо используют шкалы, ориентированные на другие типы распределений.