Geum.ru

Контрольні питання з курсу «Математичне програмування»

Вид материалаДокументы
Подобный материал:
Контрольні питання з курсу «Математичне програмування»

  1. Математична модель задачі лінійного програмування. Приклад.
  2. Графічне рішення задачі ЛП. Приклад.
  3. Визначення дифіцитних і недифіцитних ресурсів в задачі ЛП на основі її графічного рішення. Приклад.
  4. Визначення цінності ресурсів в задачі ЛП на основі її графічного рішення. Приклад.
  5. Визначення допустимого заміщення коефіцієнтів цільової функції в задачі ЛП на основі її графічного рішення. Приклад.
  6. Стандартна форма задачі ЛП. Приклад.
  7. Алгоритм рішення задачі ЛП симплекс-методом. Приклад.
  8. Рішення задачі ЛП симплекс-методом. Приклад.
  9. Знаходження початкового базисного рішення методом великих штрафів (М-метод). Приклад.
  10. Виродженність рішення задачі ЛП. Приклад.
  11. Альтернативне оптимальне рішення в задачі ЛП. Приклад.
  12. Необмежені рішення в задачі ЛП. Приклад.
  13. Відсутність допустимих рішень в задачі ЛП. Приклад.
  14. Аналіз задачі ЛП на відчутність за допомогою симплекс-таблиць.
  15. Подвійна задача ЛП. Приклад.
  16. Одержання оптимального рішення двоякої задачі ЛП за допомогою оптимальної симплекс-таблиці прямої задачі.
  17. Экономічна інтепрітація двоякості задачі ЛП.
  18. Подвійний симплекс-метод. Приклад.
  19. Рішення транспортної задачі. Приклад.
  20. Одержання початкового базисного рішення транспортної задачі методом північно-західного вузла. Приклад.
  21. Одержання початкового базисного рішення транспортної задачі методом найменшої вартості. Приклад.
  22. Рішення задачі о призначеннях. Приклад.
  23. Математична модель транспортних задач.
  24. Математична модель задачі о призначеннях.
  25. Математична модель задачі цілочисленного програмування.
  26. Метод відсікаючих площин Гомори. Графічна ілюстрація метода.
  27. Графічна ілюстрація метода.
  28. Модель динамічного програмування. Поняття стан системи. Приклад.
  29. Рекурентне співвідношення для процедури зворотньої прогонки. Приклад.
  30. Рішення задачі оптимального розподілення капіталу методом динамічного програмування.
  31. Знайти графічним методом рішення наступної задачі ЛП:

max L = 3x1+x2;

x1+2x24;

x1-x22;

x13;

x10; x20.
  1. Привести до стандартної форми наступну задачу ЛП:

min L = x1+3x2;

-2x1+5x2-5;

6x1-3x26;

x20; x1 – не обмежена в знаку.
  1. Вирішити симплекс-методом наступну задачу ЛП:

min L = x1+3x2;

x1+2x28;

x1-x26;

x14;

x10; x10.

61. Вирішити симплекс-методом наступну задачу ЛП:

max L = 3x1+x2;

3x1+x2=4;

4x1-3x26;

x1+2x24;

x10; x20.

62. Знайти двояку задачу до наступній задачі ЛП:

min L =4 x1+6x2;

2x1+3x2=6;

-2x1+8x25;

4x1+9x29;

x20; x1 – не обмежена в знаку.

63. Використовуючи двоякий симплекс-метод, знайти рішення наступної задачі ЛП:

max  = 3x1+x2;

3x1+x24;

4x1+3x28;

x10; x20.

64. Вирішити наступну збалансовану транспортную задачу:


a = |5, 3, 7, 15| : b = |2, 8, 9, 11|


c =


65. Вирішити наступну збалансовану задачу о призначеннях:


a = |1, 1, 1, 1, 1| : b = |1, 1, 1, 1, 1|


c =


66. Вирішити наступну незбалансовану транспортну задачу:


a = |5, 6, 3, 4| : b = |3, 7, 5, 6|


c =


67. Вирішити наступну збалансовану задачу о призначеннях:


a = |1, 1, 1, 1, 1| : b = |1, 1, 1, 1, 1|


c =


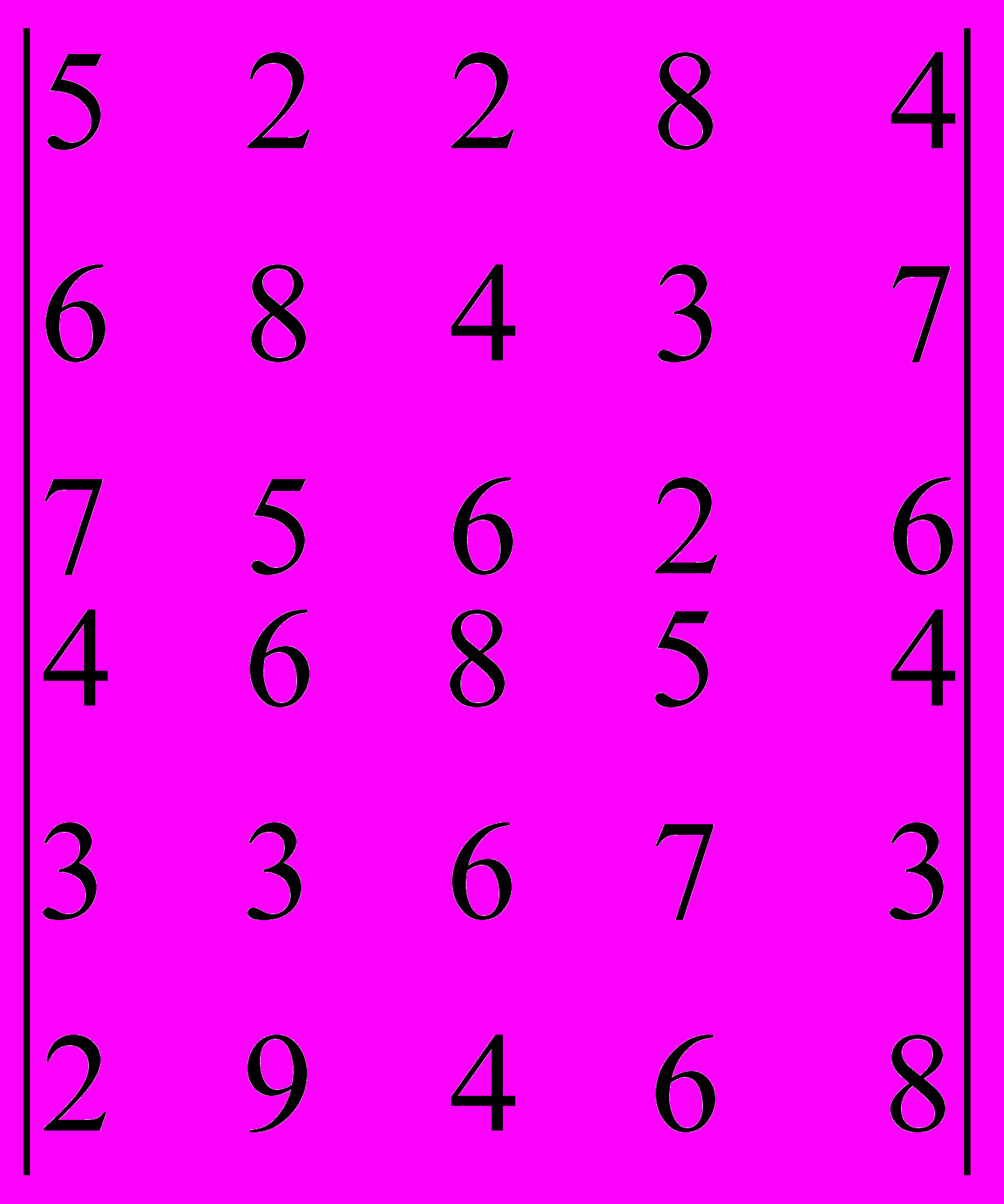
69. Вирішити графічним методом наступну задачу цілочисленного програмування:


max L = 5x1+8x2;

x1-x21;

7x1+5x235;

x1,x2 – невід’ємні цілі.


70. Вирішити, використовуючи дрібний алгоритм, наступну задачу цілочисленного програмування:

max  = x1+4x2;

x1+2x22;

3x1+5x26;

x1,x2 – невід’ємні цілі.


71. Використовуючи метод динамічного програмування знайти найкоротший шлях між пунктом А і В. Прокладання шляху можлива тільки на північ, захід і по діагоналі.





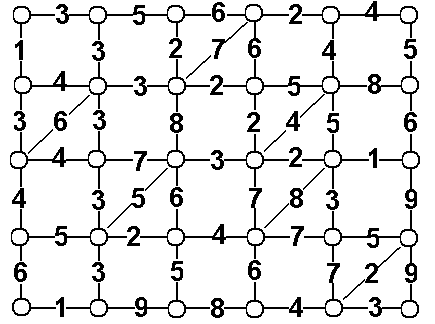
72. Використовуючи метод динамічного програмування розподілити оптимальним методом капітал К=6 тыс. грн. між трьома підприємствами (вкладаючи тільки цілі кількості засобів в тис. грн.). Функції прибутку fi(x) рівні.


x
F1(x)
F2(x)
F3(x)

0
0
0
0

1
0,3
0,1
0,6

2
0,6
1,2
1,2

3
1,2
2,4
2,4

4
2,0
2,8
3,0

5
3,4
3,0
3,1

6
4,0
3,6
3,2



73. Використовуючи метод динамічного програмування знайти оптимальний план загрузки автомобіля грузопід’ємністю 30 тонн. Вартість Сi окремих неподільних предметів і їх маса qi приведені в наступній таблиці


Номер предмету
П1
П2
П3
П4
П5
П6
П7
П8

Вага предмету, qi
4
6
8
10
12
16
18
20

Вартість предмету, тис. грн.
7
10
12
15
18
28
32
45