Творец арабского востока аль-хорезми
| Вид материала | Документы |
- «Жизнь и деятельность Ал Хорезми Мухаммед Бен Мусса (783 850)», 56.66kb.
- Около 825 года аль-Хорезми написал сочинение, в котором впервые дал описание придуманной, 46.75kb.
- Народам Арабского Востока принадлежит важное место в истории культуры человечества, 247.51kb.
- Методические указания и программа курса «история и культура народов арабского востока», 331.99kb.
- Известно, что слово алгебра произошло от названия сочинения "Китаб аль Джебр валь Мукабал", 63.82kb.
- Алгоритмизация и управление информационными процессами, 175.17kb.
- Среди всех великих мыслителей и ученых, которые обогатили область знаний периода раннего, 40.14kb.
- Махдавийат с точки зрения Ахл аль-Бейт Абд аль-Карим ал-Бахбахани, 928.02kb.
- Королевство Марокко, 167.81kb.
- "алгоритм" произошло от латинской формы имени среднеазиатского математика аль-Хорезми, 445.31kb.
ТВОРЕЦ АРАБСКОГО ВОСТОКА АЛЬ-ХОРЕЗМИ
Абдикаримова М.Б., Аринова Д.Б., Башкенова А.Г., Петрова Ю.С.
7 В, СШ23, г. Караганда
Руководитель Бухарицына Л.В.
Рождение математики и её первые шаги справедливо связывают с именами ученых Древней Греции. Но случалось и так, что свет знаний шёл из Азии, заставляя удивляться Европу. Велик вклад в средневековую науку Мухаммеда бен Мусы аль-Хорезми (787 – около 850) 1160-летие памяти которого в 2010 году.

Кстати, в самом его имени содержится определенная информация: Мухаммед, сын Мусы из Хорезма. Хорезм – земля древняя. За тысячу лет до новой эры там уже были построены магистральные оросительные каналы и искусные сооружения.
Когда в 622 г. пророк Мухаммед бежал из Мекки и стал проповедовать ислам (араб. “покорность”), ещё ничто не предвещало грядущего триумфа новой религии. Но уже к началу VIII в. арабские халифы (преемники пророка) покорили огромную территорию от Пенджаба и Хорезма на востоке до Геркулесовых столбов (Гибралтарского пролива) на западе. Первые халифы не жаловали светскую культуру и науку, в том числе – математику. И только халифы следующей династии, глубоко уважая ученость, стали приглашать в Багдат иноземных мудрецов, на арабский язык были переведены основные произведения Евклида, Архимеда, Аполлония, Герона, Птолемея и Диофанта. В VIII-IX вв. в Арабском халифате уже пользовались индийской десятичной позиционной системой. Трактат “Об индийском счете” – первый арабский труд, написанный выдающимся среднеазиатским учёным аль-Хорезми. И поскольку он был написан на общем для мусульманского мира языке – арабском, то за индийской нумерацией в Европе закрепилось неправильное название – “арабская”. Правила действий с десятичными числами получили название “алгоритм”. Это привычное для нас слово происходит от латинской формы имени аль-Хорезми.

Надо полагать, что потребность в точном сельскохозяйственном календаре, в регулировании стока воды, в планировании поливных земель заставило хорезмцев развивать математику с особым усердием, а потребности астрономии привели к бурному развитию алгебры и тригонометрии.
IX век стал временем подлинного расцвета науки в Средней Азии. Именно тогда были составлены первые тригонометрические и астрономические таблицы, проведены измерения величины Земли, строились обсерватории, появились научные труды по географии и первые географические карты. Поэтому нельзя сказать, что аль-Хорезми был одинок в своём отечестве, – он был на головы выше многих. Не зря библиотеку в Багдаде, которую он возглавлял, где были переведены труды ученых Древней Греции, Индии, Ирана назвали Домом Мудрости.
Основы алгебры как науки заложил труд аль-Хорезми “Китап аль-джебр валь-мукабала” (“Книга о восстановлении и противопоставлении”). Слово “аль-джебр” в математической литературе арабского Востока означало перенесение отрицательного члена из одной части уравнения в другую, чтобы получить в обеих частях положительные члены. Отсюда и произошло название науки – алгебра. “Аль-мукабала” переводится как “сравнение”, “противопоставление”, с точки зрения математики это операция приведения подобных членов в обеих частях уравнения. Для иллюстрации словесных алгебраических правил он использовал геометрию.
Аль-Хорезми – автор одиннадцати работ. Шесть из них дошли до нас в арабском оригинале, три – в переводах и пересказах, а две, к сожалению, были утеряны. Впрочем, аль-Хорезми занимался не только математикой. В списке его основных работ значится трактат и по астрономии, в котором он исследует движение Солнца, Луны и пяти планет, дает правило измерения геометрических широт и долгот, определяет размеры солнечного диска, рассказывает о солнечных и лунных затмениях. “Книга картины Земли” – труд географический. В нём даны координаты 2402 пунктов земной поверхности и изложена оригинальная географическая система с учетом климатических зон. К сожалению, эта книга не была известна европейцам, но её значение для развития географии на Востоке очень велико.
Историк Ибн-Халдун из Туниса писал в XIV в., что “ книга аль-Хорезми о шести типах алгебраических задач принадлежит к числу лучших книг, составленных в этой области ”. В 1145 г. алгебраический трактат был переведен на латынь. В 1842 г. сделан его перевод на французский язык. В 1857г. – перевод на немецкий, потом был сделан перевод на английский. А в XX в. эти сочинения опубликованы на русском языке. Аль-Хорезми дал классификацию линейных и квадратных уравнений и способы их решения, рассмотрев шесть видов уравнений, к которым путем алгебраических преобразований сводятся другие уравнения:
- ax2 = bx (в терминологии аль-Хорезми – “квадраты равны корням”),
- ax2 = c (“квадраты равны числу”),
- ax = c (“корни равны числу”),
- ax2 + bx = c (“квадраты и корни равны числу”),
- ax2 + c = bx (“квадраты и числа равны корням”),
- bx + c = ax2 (“ корни и числа равны квадратам”).
Здесь a, b, c > 0.
Надо признать, что труд великого ученого стал важной вехой в истории мирового математического сообщества. Но чем же еще привлекли нас, не умеющих решать квадратные уравнения, деяния гения арабского Востока?
А тем, что помимо алгебраического способа нахождения корня уравнения аль-Хорезми обычно предлагал и геометрический.
Вот, например, весьма изящное геометрическое решение уравнения
х2 + 10х = 39, относящееся к 4-му типу.
Рисуем квадрат, сторона которого обозначается неизвестной величиной х. Площадь такого квадрата х2. На сторонах квадрата строятся четыре прямоугольника со сторонами х и 10/4, а в углах – четыре квадрата со стороной 10/4 (рис.1).
Тогда площадь каждого из построенных прямоугольников будет равна
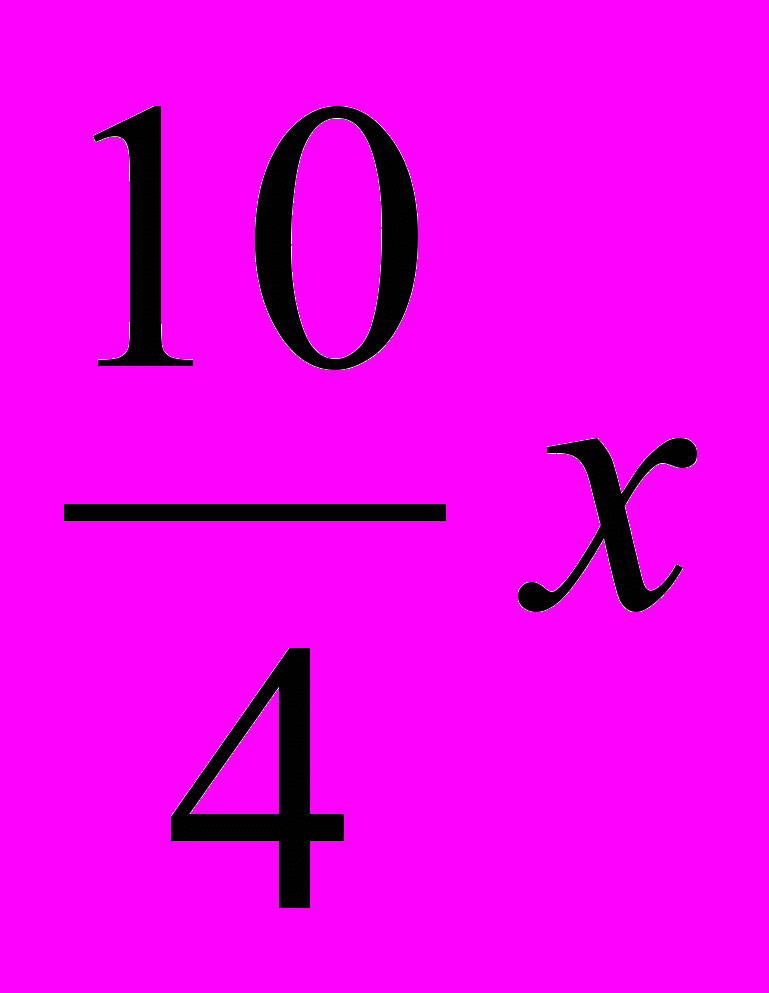 , а сумма их площадей 10х.
, а сумма их площадей 10х. Площадь каждого из четырех угловых квадратов равна
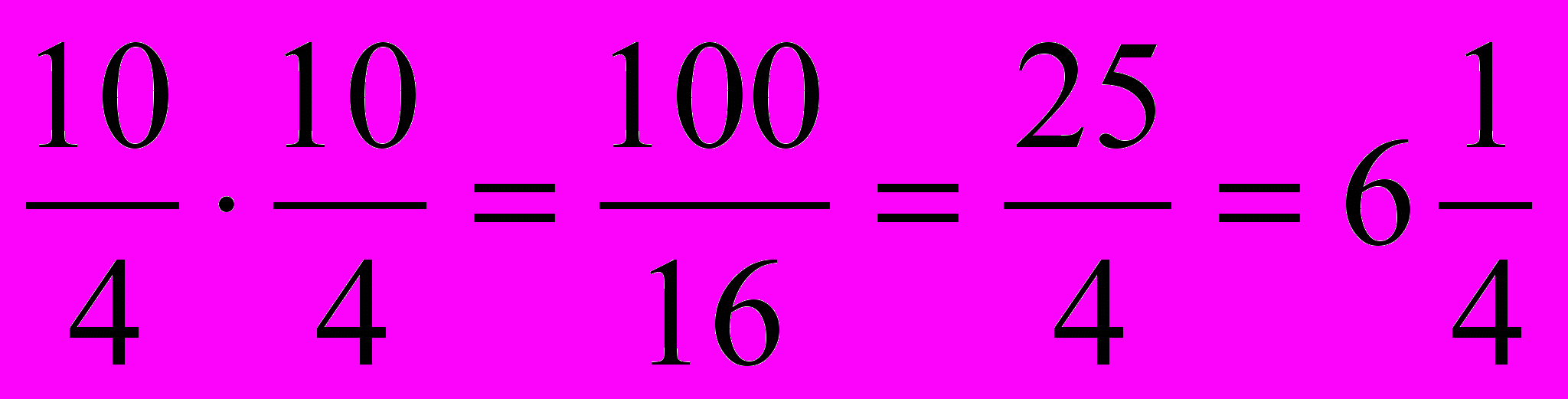 , а их сумма равна 25.
, а их сумма равна 25.Если сложить площади квадрата (х2) и четырёх прямоугольников (10х), то получится выражение, стоящее в левой части уравнения х2 + 10х = 39, т.е. суммарная площадь равна 39.
Отсюда находим, что площадь большого квадрата 39 + 25 = 64, а его сторона соответственно 8.
Из рисунка следует, что сторону большего квадрата можно выразить как сумму х +
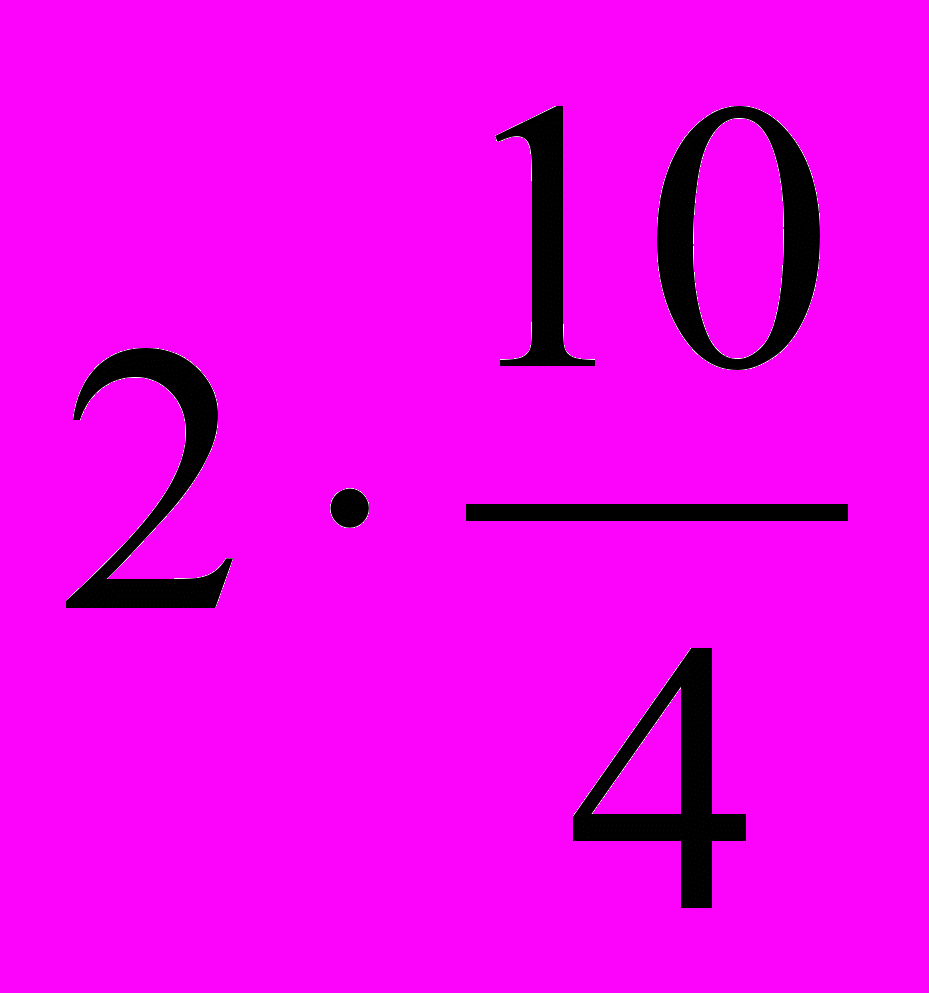 .
.Приравнивая х +
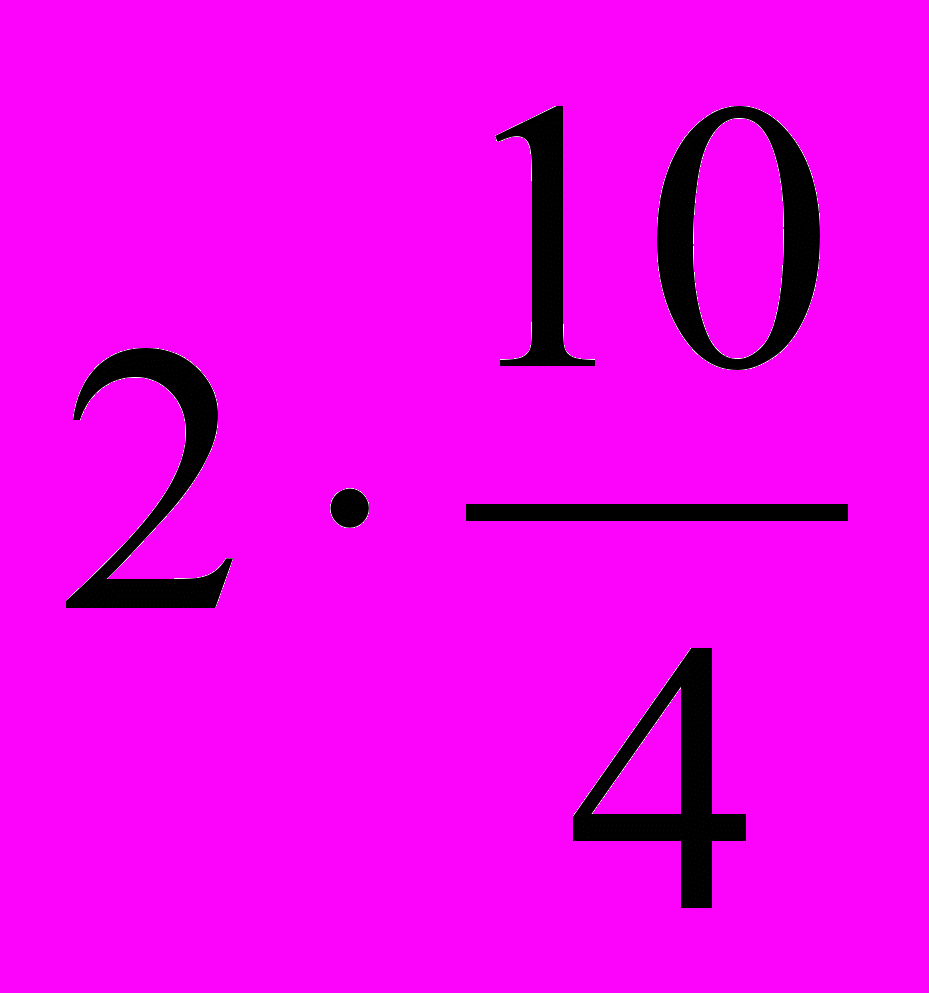 = 8, получаем х = 3.
= 8, получаем х = 3.Поверка: 32 + 10 . 3 = 39
9 + 30 = 39
39 = 39
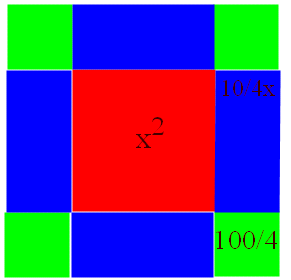
Рис.1
Математические труды аль-Хорезми высоко оценены во всём мире. Открытия творца арабского Востока подготовили почву для последующих исследований. Память человечества не сохранила, не донесла до нас имя изобретателя колеса или гончарного круга. Назвать же гения, впервые задавшего вопросом “сколько?”, тем более невозможно. Но человечество еще долго будет задавать вопросы, призванные ввести нас в таинственный и прекрасный мир математики, извлекать пользу и восхищаться её красотой!
Для этого “надо учиться, в мире люди учатся всю жизнь” [5].
Литература
- Энциклопедия для детей. Т.11. Математика/М.Д. Аксёнова. – М.: Аванта+, 2000
- Энциклопедический словарь юного математика/А.П. Савин. – М.: Педагогика, 1985
- Средняя Азия, / o.ru/heritage/horezmi?print=1-7кб
- Архив академика А.П. Ершова/ s.nsk.su/arcive/eandex.asp?did=940-9кб
- Послание Президента Республики Казахстан Н.А. Назарбаева народу “Через кризис к обновлению и развитию”/6 марта 2009года, г. Астана
