П. И. Бондаренко Планковские величины
| Вид материала | Документы |
- План: Характеристика основных видов относительной величины. Требования к статическому, 91.5kb.
- О. Ю. Бондаренко // Клинич перспективы гастроэнтерологии, гепатологии. 2006. N c. 24-27, 47.42kb.
- Строительные материалы, 207.69kb.
- Cols=2 gutter=93> Бондаренко, 94.59kb.
- 1 Оплата труда в бюджетном секторе, 3504.84kb.
- Правила оформления дипломной работы 9 Подготовка к защите и защита дипломных работ, 482.95kb.
- В. П. Астафьев «Пролетный гусь»: Рассказ, 80.18kb.
- Бухгалтерский отчёт План счетов Первичный документ Вкачестве регистраторов могут выступать, 109.43kb.
- Вопросы к экзаменам 3-й курс вмк вопросы для темы, 70.75kb.
- Хнуре видатні науковці Михайло Федорович Бондаренко Біобібліографічний покажчик Харків, 638.34kb.
П. И. Бондаренко
Планковские величины
Вернемся к статье Зельдовича и Новикова:
«Более принципиально важной проблемой теории строения Вселенной является проблема квантовых эффектов в сверхсильных гравитационных полях.
В какой области можно ожидать существенных эффектов? ОТО не вносит в теорию новых физических констант, кроме уже известных (Космологическая постоянная, если она отлична от нуля, существенна лишь в очень больших масштабах, где нет квантовых явлений.): скорости света с и ньютоновской постоянной G. Планк ввел свою знаменитую постоянную h в теорию излучения в 1899 г. (сейчас принято пользоваться величиной
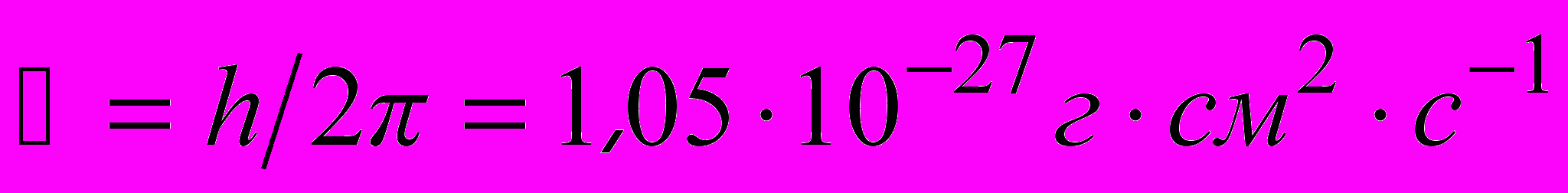). Он отчетливо понимал значение идеи квантования для всей физики, всего естествознания.Рассматривая
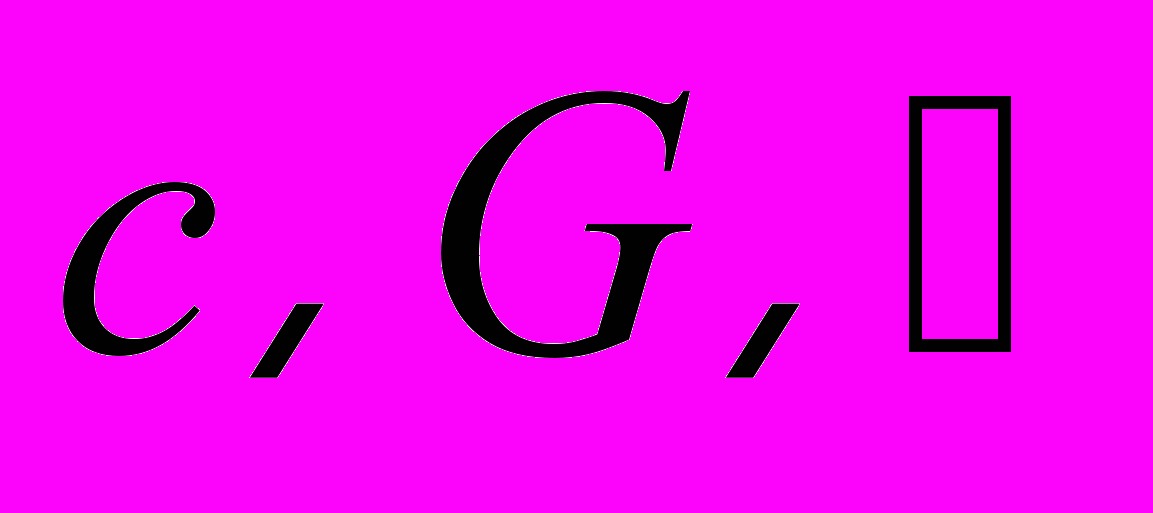как три равноправные фундаментальные величины, Планк показал, что через них могут быть выражены величины любой размерности. В частности, через 
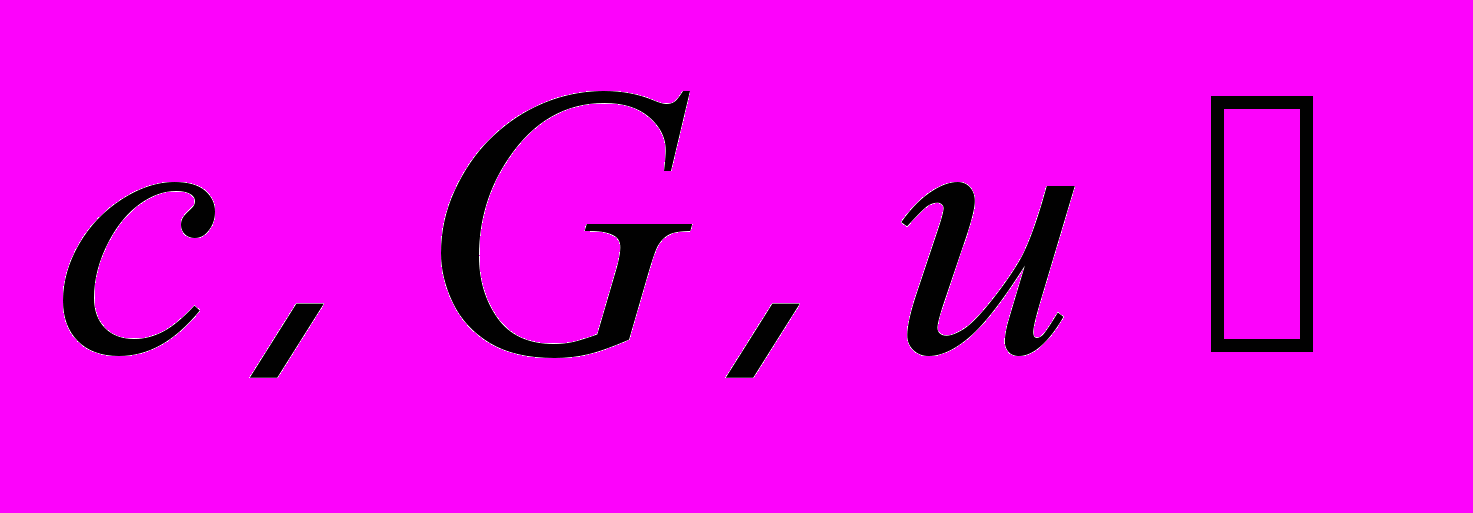можно выразить единицу длины 
, времени 
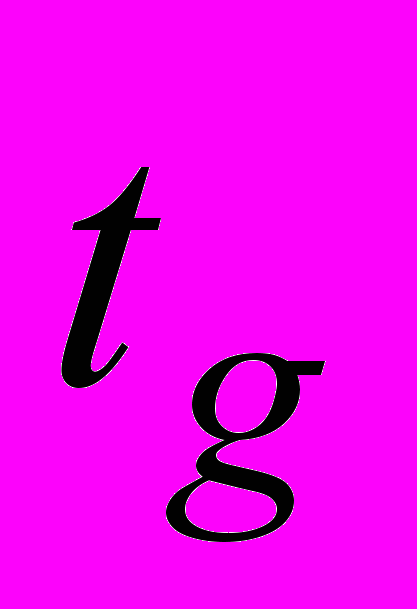, массы 
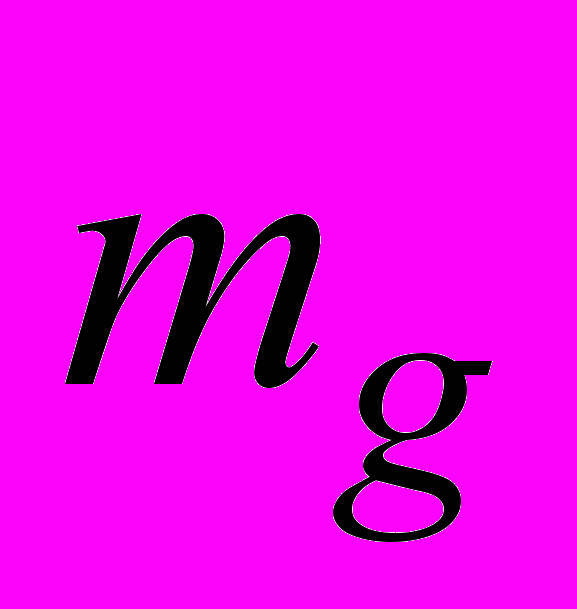, плотности 
:
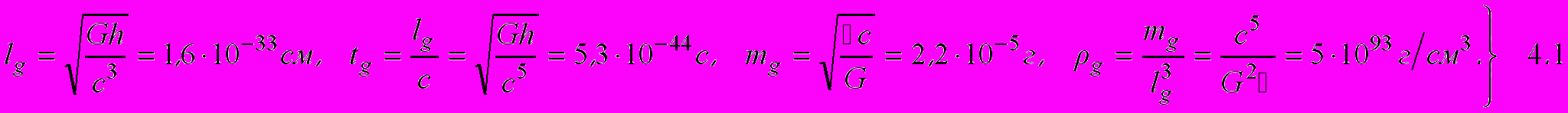Напомним, что для элементарных частиц 
, 
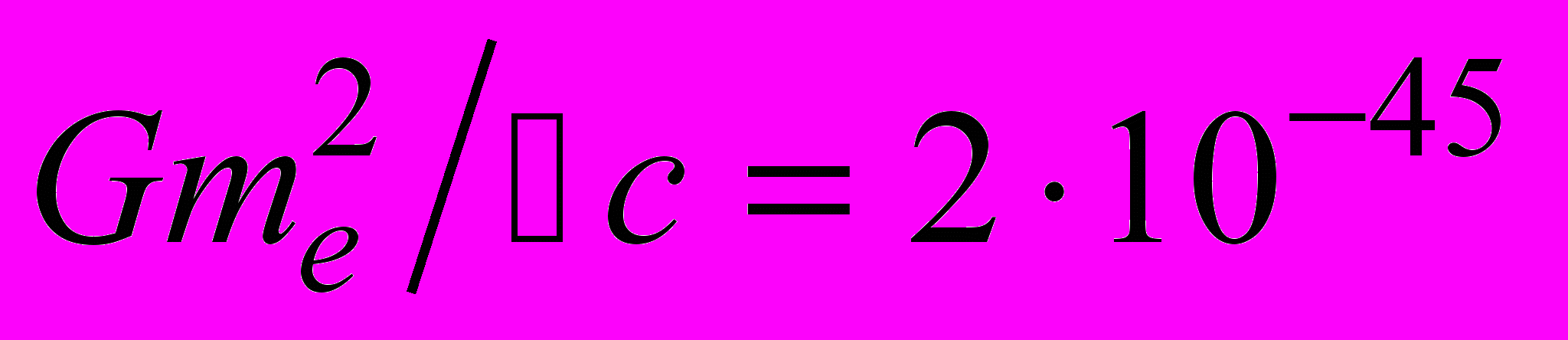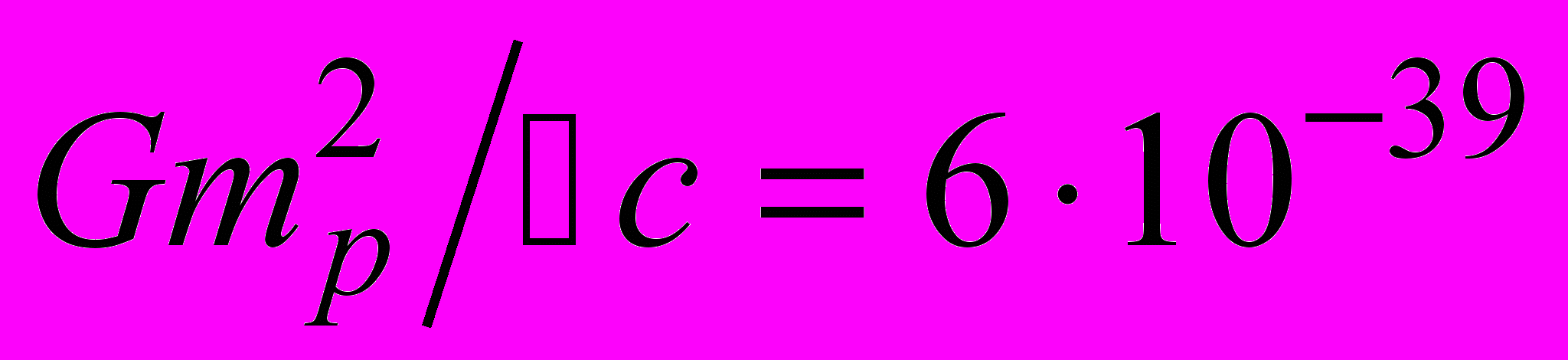. Условие 
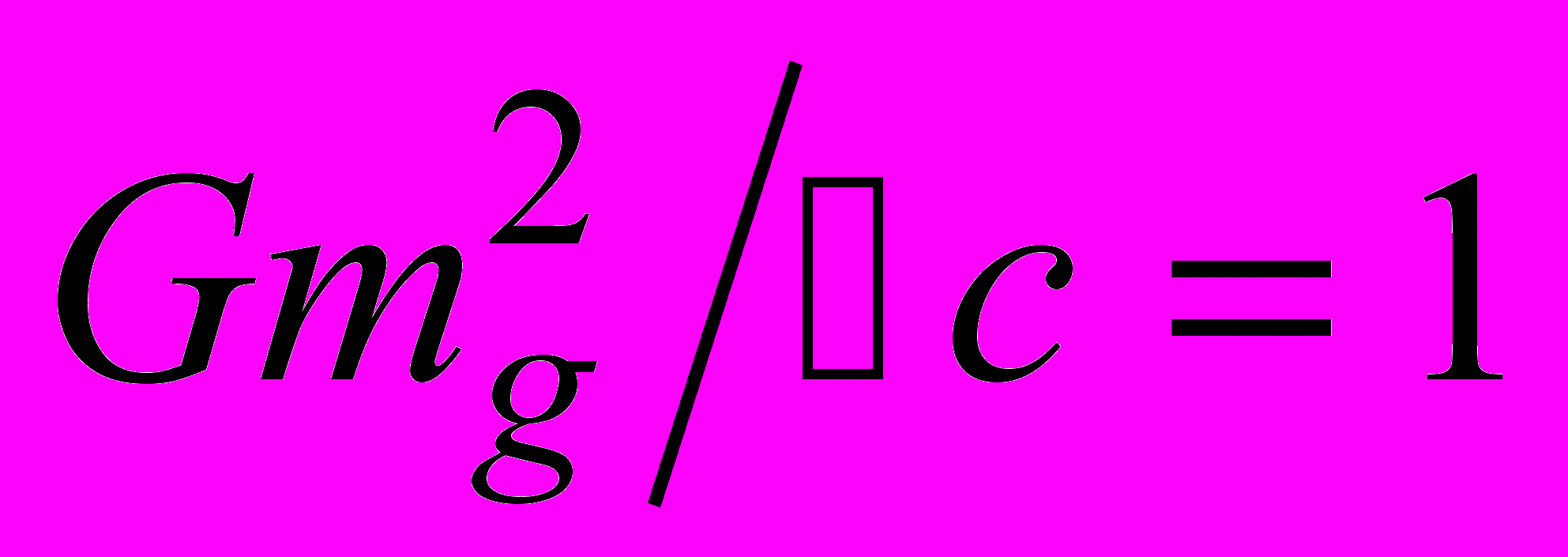дает характерную массу 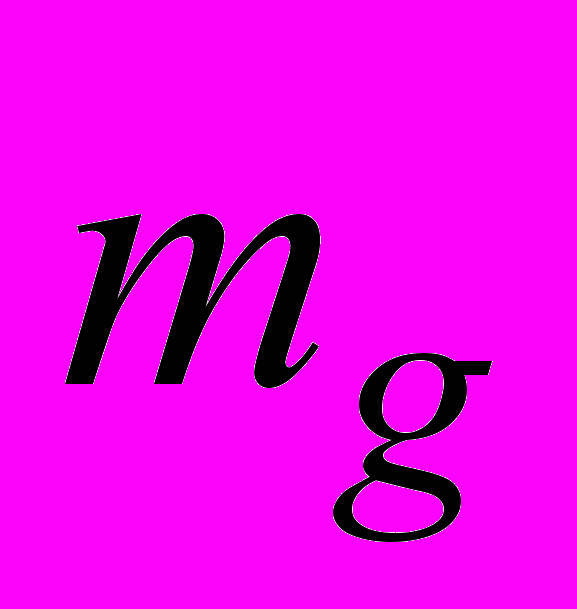приведенную выше. Длина 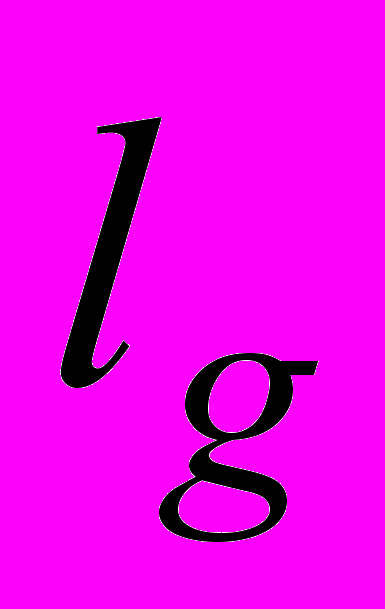есть комптоновская длина волны массы 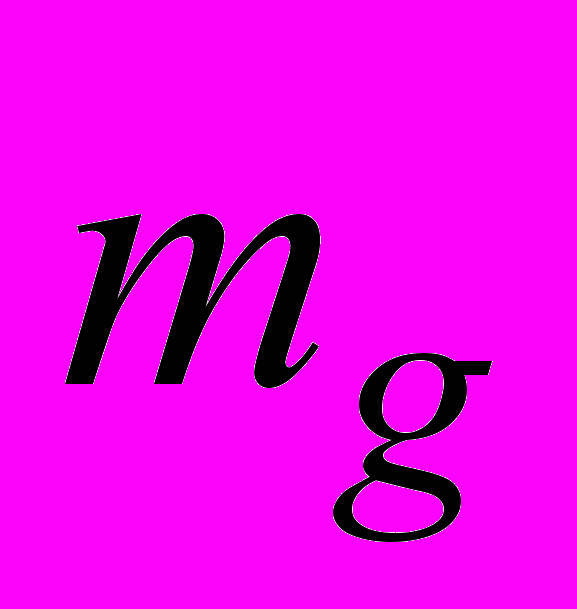, а именно 
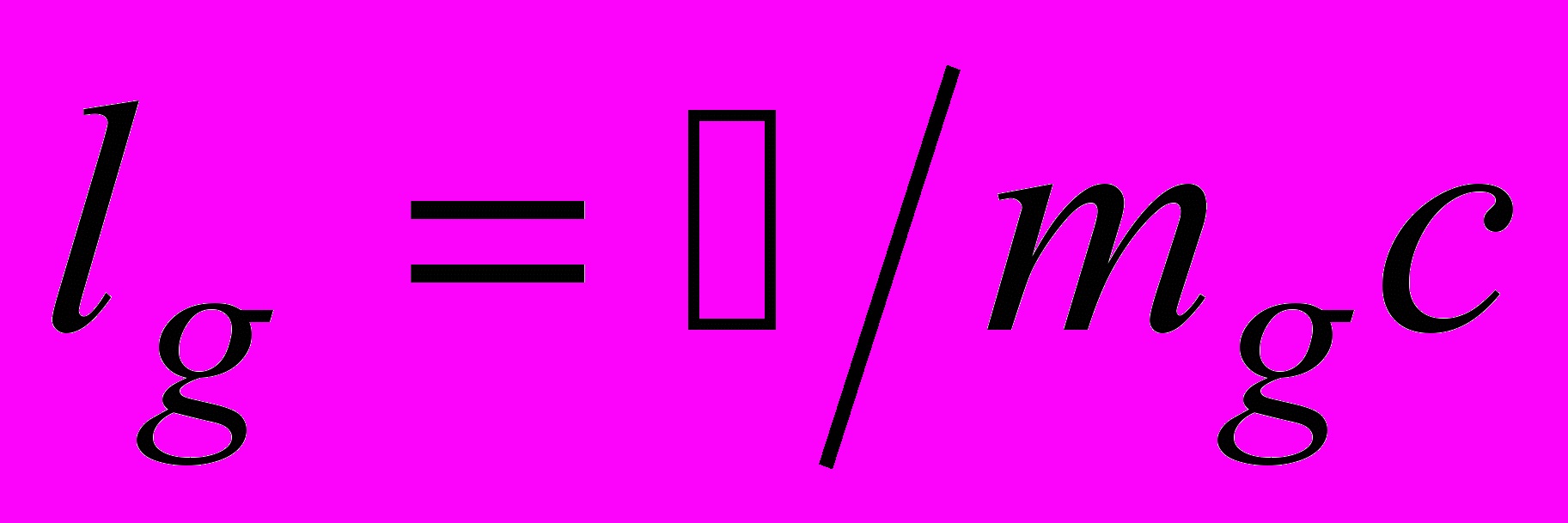. Наконец, в теории элементарных частиц применяется еще один способ выражения. Примем 
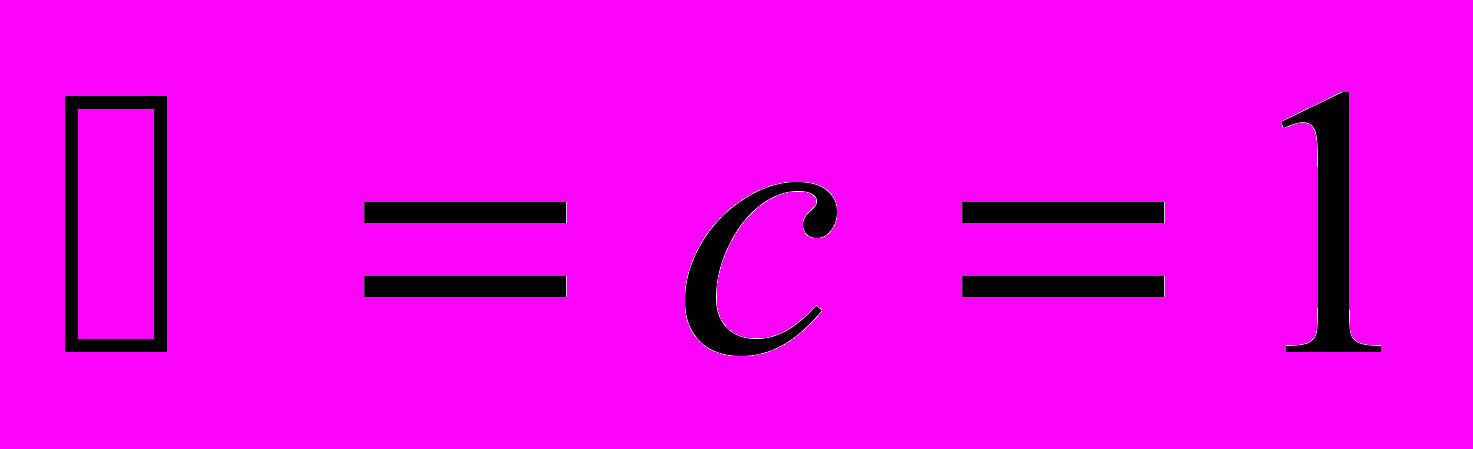. В такой системе единиц длина и время имеют одинаковую размерность, обратную размерности массы, 
. Произведение 
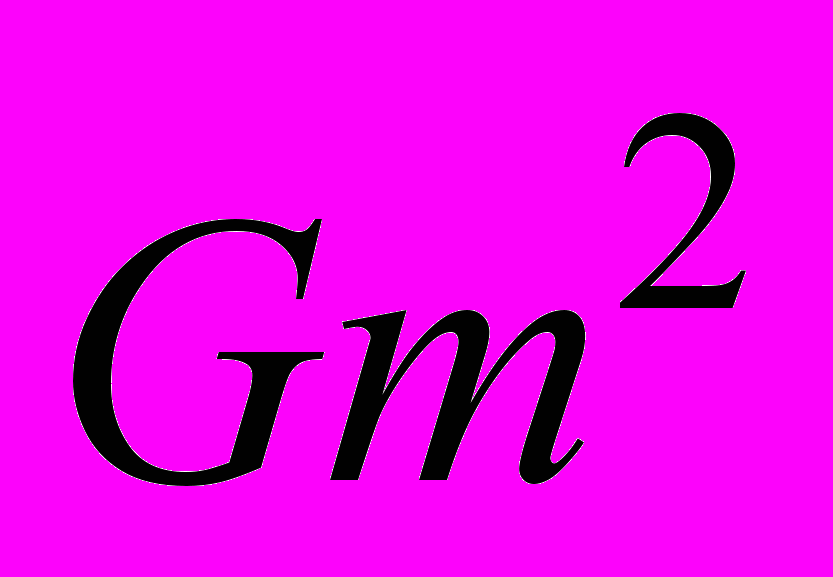безразмерно, следовательно, размерность G есть 
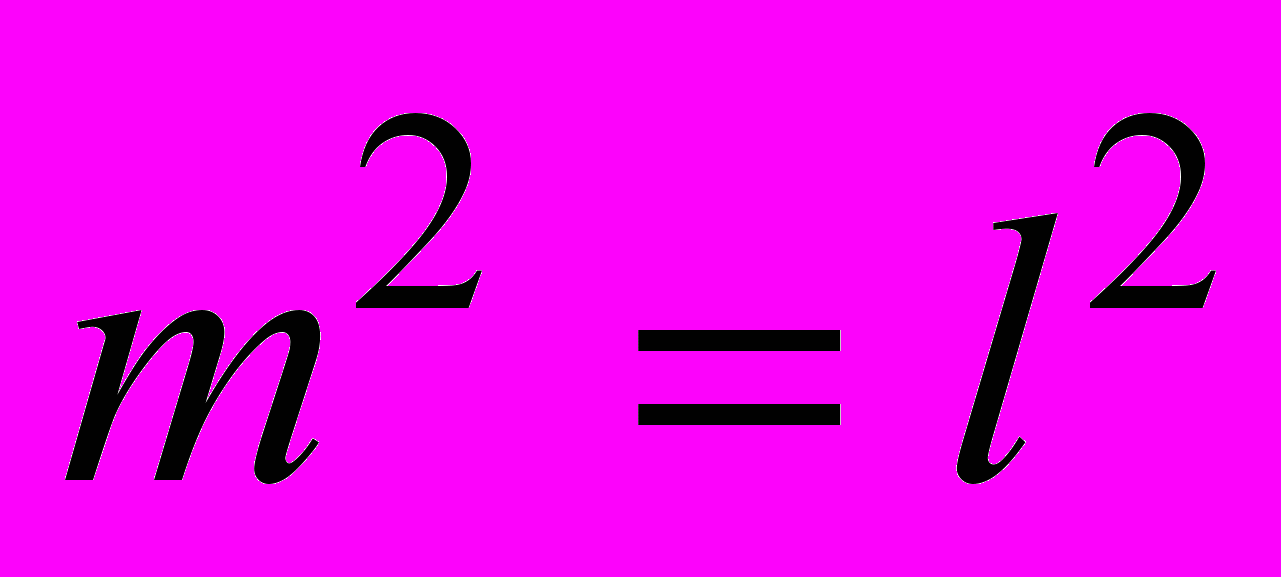. Соответствующие G «площадь» и «сечение» равны 
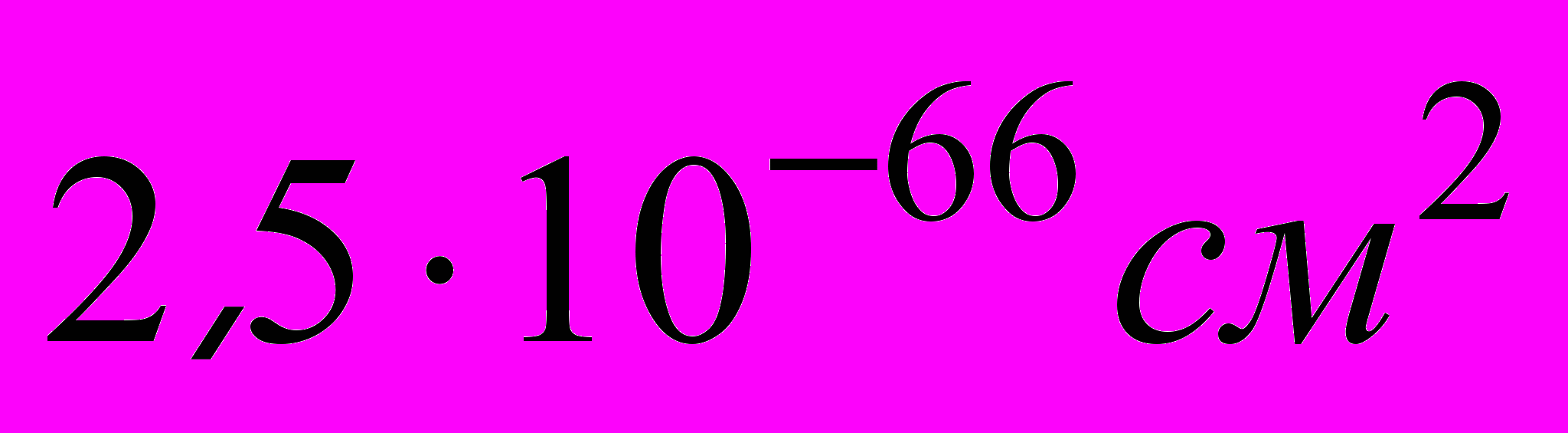.Эти величины характеризуют область, в которой принципиальную роль играют квантовые эффекты в гравитации: нужно, чтобы кривизна пространства-времени была порядка
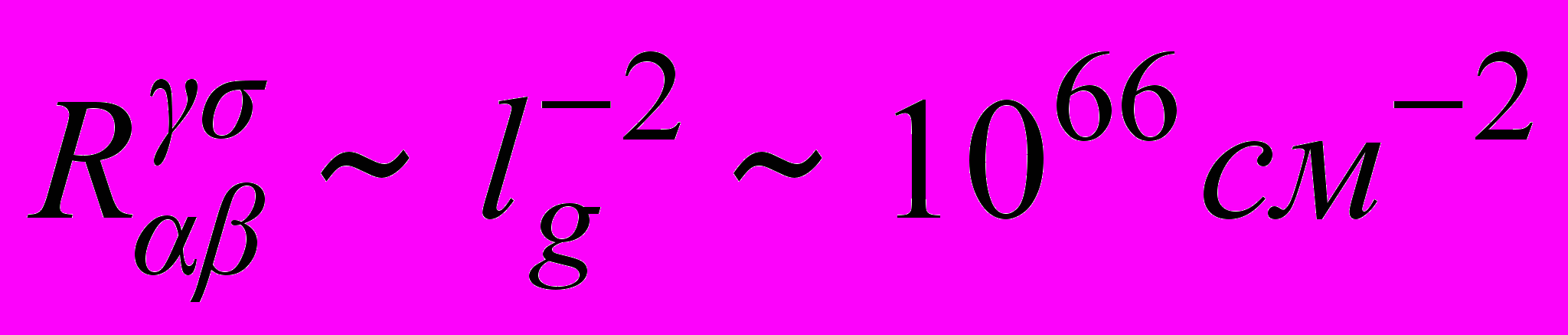. Такая ситуация должна возникнуть, если плотность вещества достигает порядка 
. Соответствующая кривизна (порядка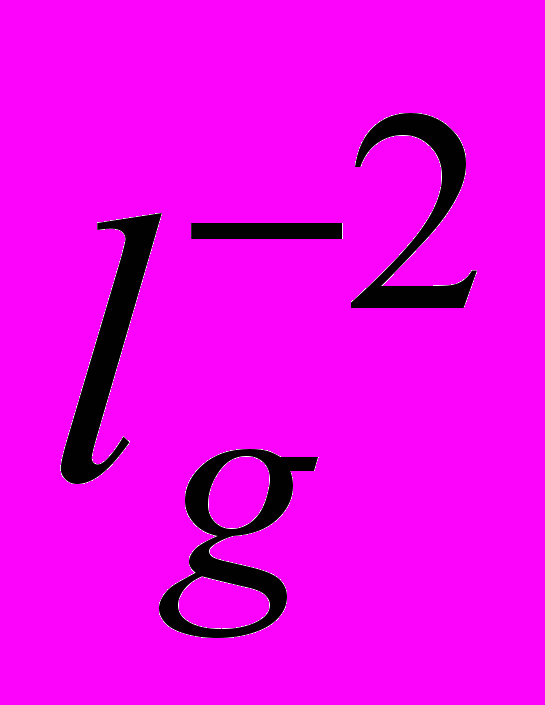 
) следует из уравнений ОТО и в этом смысле «обязательна». Насколько просто найти область, где важны квантовые явления, настолько же трудно выяснить, что именно происходит в этой области [С. де Витт, Уиллер (1968), Гинзбург, Киржниц, Любушин (1971)]. Здесь становится даже трудно сформулировать проблему. Обратимся к космологии. Вселенная начала расширяться около 10 миллиардов лет назад от сингулярного состояния сверхбольшой плотности материи и сверхбольших кривизн пространства-времени. Из сказанного выше ясно, что в сингулярном состоянии начала расширения квантовые эффекты должны играть определяющую роль. Однако природа сингулярного состояния совершенно не ясна, так же как неясно, что было до этого, и неясно даже, можно ли ставить этот вопрос.
В космологии выход состоит в том, чтобы задавать вопросы (и вычислять величины), относящиеся к тому периоду, когда мир уже вышел из сингулярного состояния когда нигде нет ни грандиозной кривизны, ни огромной плотности материи. Квантово-гравитационная теория необходима именно в космологии, поскольку имеется уверенность, что Вселенная (по-видимому, можно даже усилить: вся Вселенная, все вещество Вселенной!) прошла через состояние, анализ которого требует этой теории. Такое рассмотрение тем более необходимо, что велико разнообразие классических (не квантовых) космологических решений. Может быть, квантово-гравитационная теория сингулярного состояния укажет условия выбора из этого множества. Законченной квантово-гравитационной космологической теории в настоящее время не существует, есть лишь отдельные результаты.
В ряде работ развивается логическая схема такой теории и вычисляются квантово-гравитационные поправки к величинам, наблюдаемым в лабораторных опытах. Первый шаг был сделан в 30-х годах; была проквантована линейная теория гравитационных вон. При этом гравитационные волны рассматривались как малые возмущения геометрии плоского пространства или как постороннее (не геометрическое) тензорное поле, вложенное в плоское пространство. С сегодняшней точки зрения результаты тривиальны: энергия гравитонов равна
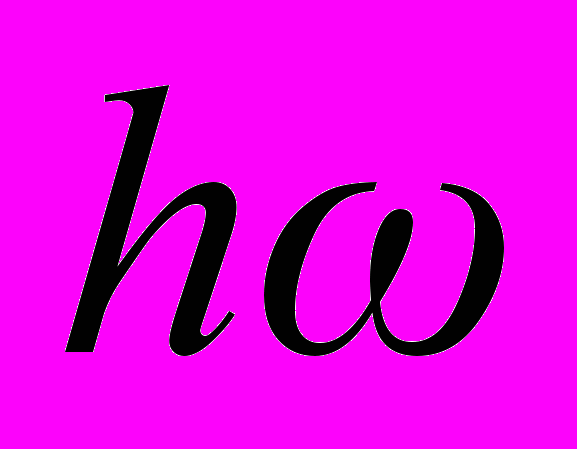, они являются бозонами со спином ² и нулевой массой покоя и т. п. В следующем порядке оказывается существенной нелинейность исходной классической теории (ОТО): гравитоны сами обладают массой и импульсом (хотя масса покоя их и равна нулю) и являются, следовательно, источником гравитационного поля. Последовательный учет этого факта начат Р. Фейнманом и продолжен Л. Д. Фаддеевым, В. Н. Поповым, Б. С. Де Виттом и др.Специфические квантово-гравитационные эффекты в лабораторной физике (да и в астрофизике, за вычетом теории сингулярностей) малы. Деятельность Р. Фейнмана и ряда других авторов вдохновлялась скорее эстетическими целями, стремлением к логически замкнутой теории, что Фейнман и не скрывает. В космологии ситуация существенно иная: при
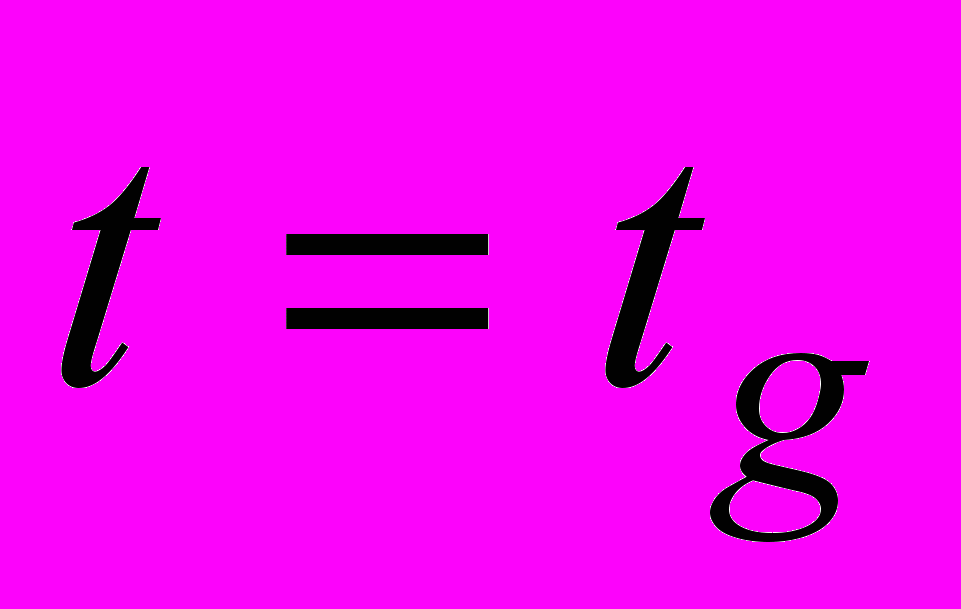квантово-гравитационные эффекты порядка единицы, и имеет интерес даже грубое представление о характере этих эффектов. Наиболее важным эффектом, вероятно, является рождение частиц и пар частиц в сильных гравитационных полях.Еще раз подчеркнем, что теория процессов вблизи сингулярного состояния далеко не является законченной и многие принципиальные вопросы остаются еще без ответа. Одним из таких нерешенных вопросов остается вопрос об однородности Вселенной в большом масштабе».
Чтобы не быть голословными, рассмотрим математическую сторону вопроса. Вернемся к планковским величинам (4.1). В нашей планетарной сферической модели пространства с ее мазутом и поплавками можно выделить 8 равносторонних треугольников. Четыре треугольника можно отождествить с четырехмерным пространством общей теории относительности и добавить к ним еще одно такое же пространство (с учетом спина гравитонов, равного 2). В результате получаем две системы отсчета, две системы координат (см. рис. 4.1).С учетом этой поправки квадрат планковской длины определим следующим образом:
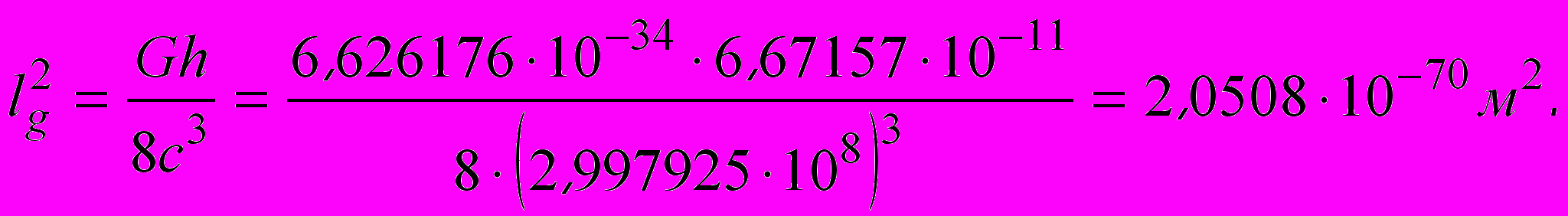(4.2)
Мы полагаем, что квадрат планковской величины определяет скорость распространения волны отдельного невзаимодействующего нуклона (протона). При взаимодействии протона со всей массой Солнца (с учетом коэффициентов о которых подробно сказано в статье «Волновое пространство») скорость распространения волны протона равна длине волны фотонов солнечного излучения максимальной интенсивности при эффективной температуре Солнца ~5875K:
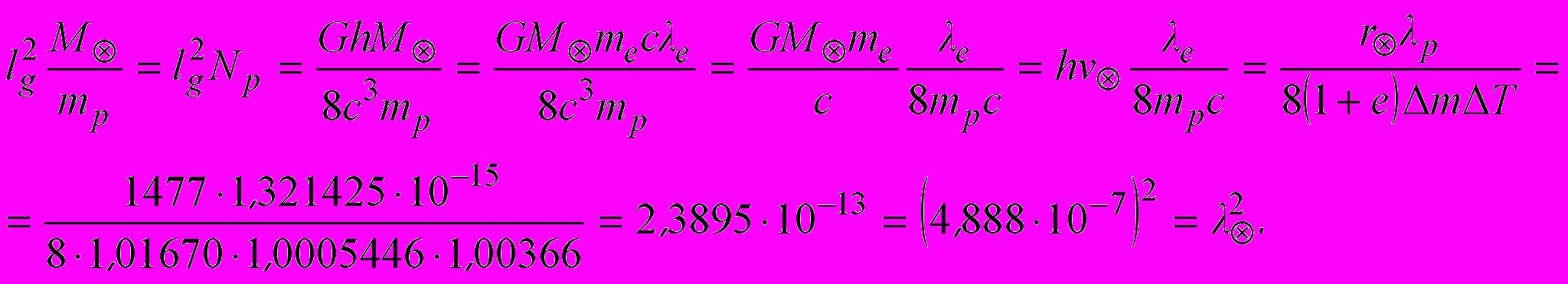(4.3)Скорость распространения волны протона при его взаимодействии со всей массой Вселенной
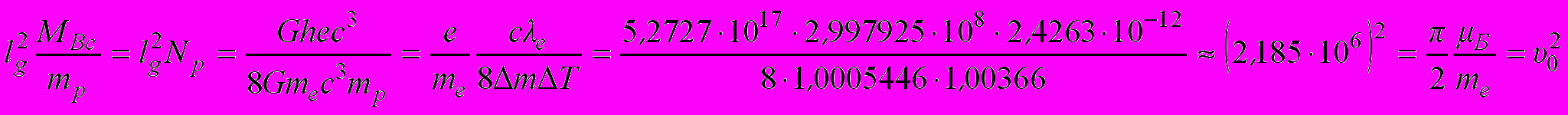(4.4)равна отношению магнетона Бора к массе электрона или скорости электрона на первой боровской орбите.
Поделим величину планковской массы в четвертой степени на квадрат планковской частоты и на массу электрона в кубе:
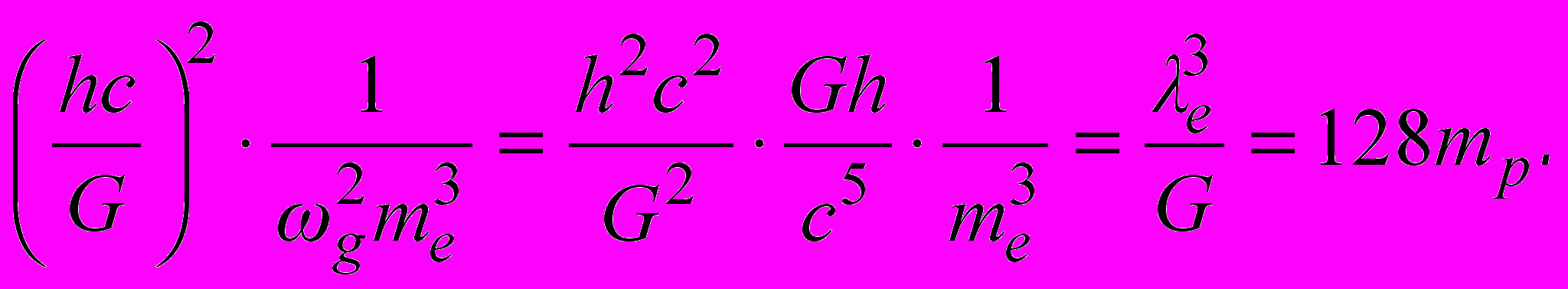(4.5)Таким образом, величина планковской массы определяется выражением
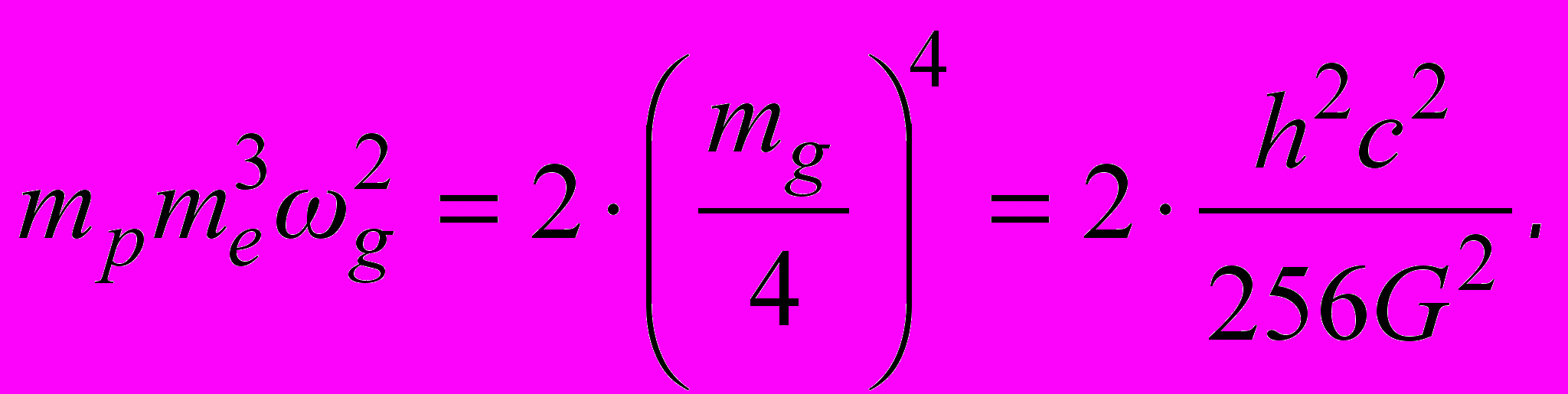(4.6)Квадрат планковской частоты
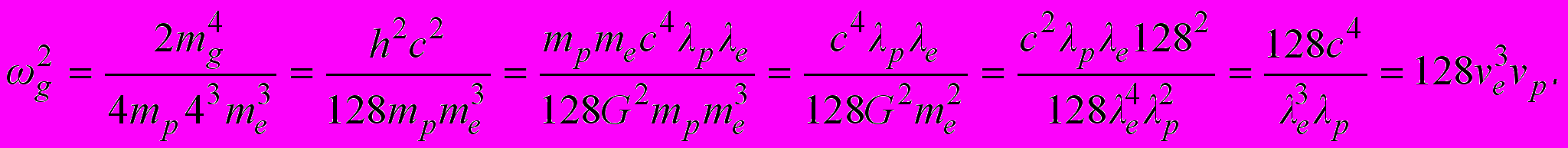(4.7)Квадрат планковской частоты можно определить также по формуле
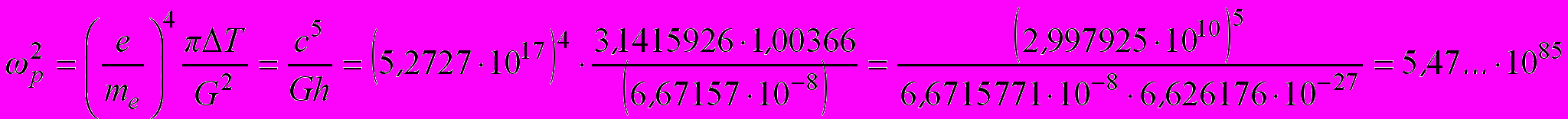(4.8)Планковскую величину плотности можно вычислить также по формулам
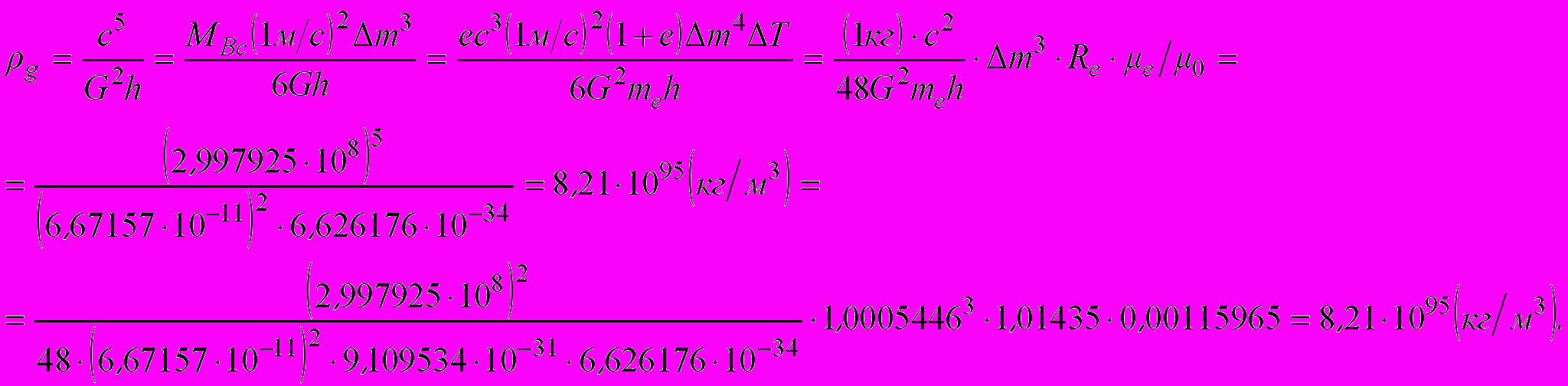(4.9)Подробное описание использованных здесь коэффициентов см. на сайте в разделе «Волновое пространство»
Резюмируя, мы не считаем верными представления современной космологической теории о некоторой выделенной (преимущественной) единственной точке сингулярного состояния материи с большой плотностью, предшествующей Большому взрыву в теории расширяющейся Вселенной. Мы полагаем, что каждому телу, находящемуся на эквипотенциальной поверхности статической Вселенной, можно приписать сингулярное состояние в соответствии с результатами, полученными Эйнштейном при анализе модели де Ситтера.