Урок на семинаре: «Правильные многогранники»

Вид материала

Подобный материал:

Муниципальное общеобразовательное учреждение

средняя общеобразовательная школа №37

Открытый урок на семинаре:

«Правильные многогранники»

Учитель математики

первой квалификационной

категории

Баталовой Е.А.

Томск – 2005

Тема: «Правильные многогранники»

Цель урока:

1. Формирование умений делать обобщения на основе полученных данных в результате исследования, выбор правильных утверждений из нескольких данных.

2. Развитие творческой активности учащихся, создание условий для проявления инициативы в выборе заданий, в выдвижении собственных предложений при различных видах деятельности.

3. Воспитание у обучающихся стремления к самосовершенствованию, удовлетворению познавательных потребностей.

Тип урока: Усвоение новых знаний

Оборудование:

1. Учебник. Геометрия, 10-11 классы.

2. Модели правильных и полуправильных многогранников, развертки правильных и полуправильных многогранников.

3. Репродукции картин Сальвадора Дали «Тайная вечеря», «Гиперкубическое распятие», А. Дюрера «Меланхолия», портрет И. Кеплера, изображение скульптуры «Платон».

4. Таблицы, изображение «Космический кубок» Кеплера (модели Солнечной системы)

5. Заготовки для выполнения моделей правильного многогранника.

Правильных многогранников

вызывающе мало,

но этот весьма скромный по

численности отряд сумел

пробиться в самые глубины

различных наук.

Л. Кэролл

I. Вступительное слово учителя.

Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности – от двухлетнего ребенка, играющего деревянными кубиками, до зрелого математика, наслаждающегося чтением книг о многогранниках. И это вы ещё раз доказали выполняя свои работы по теме «Использование многогранников в нашей жизни». Все ваши работы очень индивидуальны и интересны. Вашему вниманию представлены две работы о применении многогранников. Будьте, пожалуйста, внимательны, при повторении теоретического материала.

Спасибо за работы.

А сегодня на уроке мы познакомимся с правильными многогранниками, для этого в течение недели работали группы: 1 группа – историки, 2 группа – математики, 3 группа – исследователи космической теории Платоновых тел, теории Кеплера, 4 группа – биологи и географы, 5 группа – архитекторы и 6 группа – искусствоведы. А для начала

определим объект нашего исследования: правильные многогранники.

Я прошу группу «математиков» дать понятие правильного многогранника и определить, некоторые их свойства.

Ученик.

В учебнике «Геометрия, 10-11 классы» дается такое определение правильного многогранника «Выпуклый многогранник называется правильным, если все его грани – правильные многоугольники и в каждой его вершине сходится одно и то же число ребер».

В природе известны пять правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.

Изучая любые многогранники, необходимо конечно же определить его свойства, для этого предлагаю определить количество граней, ребер и вершин. Подсчитаем и мы число указанных элементов правильных многогранников и зафиксируем результаты в таблице 1.

Таблица 1

Правильный многогранник	Число граней	Число вершин	Число ребер
Тетраэдр	4	4	6
Куб	6	8	12
Октаэдр	8	6	12
Додекаэдр	12	20	30
Икосаэдр	20	12	30

Рассматривая табл. 1, зададимся вопросом: «нет ли закономерности в возрастании чисел в каждом столбце?» По-видимому, нет. Вот в столбце «грани» все сначала пошло хорошо (4 + 2 = 6, 6 + 2 = 8), а потом намеченная закономерность «провалилась» (8 + 2). В столбце «вершины» нет даже стабильного возрастания. Число вершин то возрастает (от 4 до 8, от 6 до 20), а то и убывает (от 8 до 6, от 20 до 12). В столбце «ребра» закономерности тоже не видно. Но не будем сдаваться. У нас еще есть поле для эксперимента. Ведь мы сравнивали числа внутри одного столбца. Но можно рассмотреть сумму чисел в двух столбцах, хотя бы в столбцах «грани» и «вершины» (Г + В). Сравним новую таблицу своих подсчетов (см. табл. 2).

Вот теперь закономерность видна.

Правильный многогранник	Сумма граней и вершин	Число ребер
Тетраэдр	4+4=8	6
Куб	6+8=14	12
Октаэдр	8+6=14	12
Додекаэдр	12+20=32	30
Икосаэдр	20+12=32	30

Сформулируем ее так: «Сумма числа граней и вершин равна числу ребер, увеличенному на 2»: Г + В = Р + 2.

Итак, получена формула, которая была подмечена уже Декартом в 1640 г., а позднее переоткрыта Эйлером (1752), имя которого с тех пор она и носит. Формула Эйлера верна для любых выпуклых многогранников.

Конечно, кроме этого свойства необходимо отметить, что ребра правильного многогранника равны между собой и что равны также все двугранные углы, содержащие две грани с общим ребром. Следовательно, радиус вписанной и описанной сферы многогранника совпадают.

Зададимся теперь вопросом о том, сколько правильных многогранников существует. Рассматривая многогранник, видим, что каждая вершина может принадлежать трем и более граням, иначе не получается пространства.

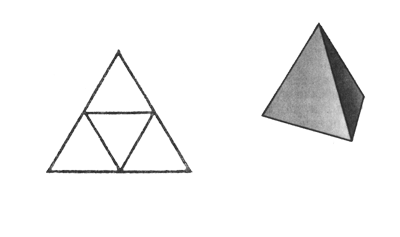
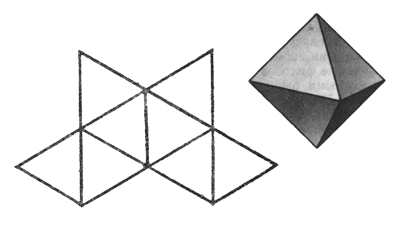
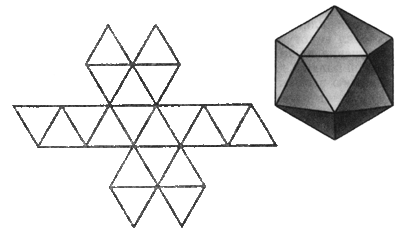
Сначала рассмотрим случай, когда грани многогранника - равносторонние треугольники. Поскольку внутренний угол равностороннего треугольника равен 60°, три таких угла дадут в развертке 180°. Если теперь склеить развертку в многогранный угол, получится тетраэдр - многогранник, в каждой вершине которого встречаются три правильные треугольные грани. Если добавить к развертке вершины еще один треугольник, в сумме получится 240°. Это развертка вершины октаэдра. Добавление пятого треугольника даст угол 300° - мы получаем развертку вершины икосаэдра. Если же добавить еще один, шестой треугольник, сумма углов станет равной 360° - эта развертка, очевидно, не может соответствовать ни одному выпуклому многограннику.

Теперь перейдем к квадратным граням. Развертка из трех квадратных граней имеет угол 3x90°=270° - получается вершина куба, который также называют гексаэдром. Добавление еще одного квадрата увеличит угол до 360° - этой развертке уже не соответствует никакой выпуклый многогранник.

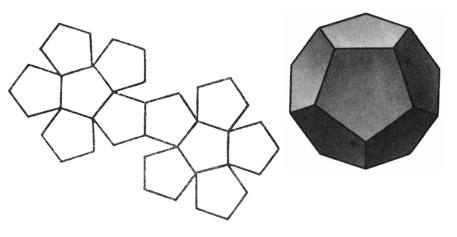
Три пятиугольные грани дают угол развертки 3*108°=324° - вершина додекаэдра. Если добавить еще один пятиугольник, получим больше 360°.

Для шестиугольников уже три грани дают угол развертки 3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует. Таким образом, мы убедились, что существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями.

Учитель

Спасибо, ребята правильно отметили очень важные свойства правильных многогранников. А я для вас выразила радиусы через сторону, а вы дома докажите эти формулы. А теперь слово группы «архитекторов».

Ученик.

От имени группы «архитекторов» предлагаю вам познакомиться с моделями (развертками) правильных многогранников, с помощью которых мы сделали модели многогранников и желаем, чтобы вы тоже склеили данные многогранники и украсили свои например ёлки.

Для изготовления моделей наша группа воспользовалась рекомендациями, данными в книге М. Винниджера «Модели многогранников», М., 1975. «Автор этой книги, заражая своим энтузиазмом читателя, дает ему ясные и четкие указания о том, как изготовить модели различных многогранников. Объяснения проиллюстрированы фотографиями моделей из собрания автора – возможно, наиболее полного в настоящее время. Но фотографии не в состоянии передать всего великолепия самих моделей. В книге представлены не только правильные многогранники, но и полуправильные у которых все многогранные углы равны, а грани – правильные многоугольники нескольких видов и правильные не выпуклые многогранники называемые звёздчатыми.

М. Винниджер отмечает: «Время, которое затратил на изготовление моделей невыпуклых однородных многогранников, в существенной степени зависело от характера модели. Так, на простейшие из них требовалось не более трех-четырех часов, а в среднем же приходилось затрачивать восемьдесят часов, а некоторые сложные модели занимали двадцать-тридцать часов. Две модели отняли у меня свыше сотни часов каждая. Теперь, когда работа завершена, я, пожалуй, соглашусь с тем, что ее объем поразил и меня. Но китайская пословица гласит «Если ты собираешься пройти тысячу ли, начни с того, что сделай первый шаг». За первым шагом последует другой, и вскоре красота открывшихся взору путника видов заставит его забыть о трудностях пути».

Наряду с правильными многогранниками существуют еще многогранники. Они не могут быть отнесены к правильным – их называют полуправильными многогранниками (тела Архимеда).

Разрешите назвать тела Архимеда и показать их изображение.

1. Усеченный тетраэдр. Он получается при сечении тетраэдра плоскостями. Гранями являются треугольники и шестиугольники.

2. Усеченный октаэдр. Он получается при сечении правильного октаэдра плоскостями. Гранями являются квадраты и шестиугольники.

3. Усеченный гексаэдр. Этот многогранник представляет собой усеченный куб, гранями являются треугольники и восьмиугольники.

4. Усеченный икосаэдр. Это усеченный вариант икосаэдра. Гранями являются пятиугольники и шестиугольники.

5. Усеченный додекаэдр. Гранями являются треугольники и десятиугольники.

Кроме этих к Архимедовам телам относятся: кубооктаэдр. Само название многогранника указывает на некоторую близость его к кубу и к октаэдру. Важнейшим свойством этого многогранника является то, что он имеет грани двух типов, причем каждая грань одного типа соседствует только с гранями другого типа. Многогранники, обладающие этим свойством, называются квазиправильными. Икосододекаэдр, ромбокубооктаэдр, ромбоусеченный икосододекаэдр (этот многогранник часто называют также усеченным додекаэдром. Гранями являются квадраты, шестиугольники и десятиугольники и другие Архимед выделил 13 полуправильных многогранников.

Но в настоящее время находят все новые и новые полуправильные многогранники. Так математик В.Г. Ашкинузе нашел еще один полуправильный многогранник. Если в многограннике ромбокубооктаэдр верхнюю «восьмиугольную чашу» повернуть на 45º, то получим многогранник, который «не совсем архимедово» тело: он не обладает некоторыми свойствами, которыми обладают тела Архимеда, но зато у него есть свои свойства.

Так же разрешите представить звездчатые многогранники. Большой звездчатый

додекаэдр, Большой икосаэдр, Большой додекаэдр, Малый звездчатый додекаэдр.

Учитель

В сообщении учеников отмечалось, что правильные многогранники называются Платоновыми телами. Значит, они занимают видное место в философской картине мира, разрабатываемой великим мыслителем Древней Греции Платоном.

Слово предоставляется «историкам», которые подготовили сообщение о философской картине мира Платона, а я хочу обратить ваше внимание на доминанту оригинальности Платона, которая и сегодня остается злободневной

- «Не золото надо завещать детям, а наибольшую совестливость»;

Ученик.

Итак, правильных многогранников Платон знал пять, а число стихий (огонь, воздух, вода и земля) было ровно четыре. Следовательно, из пяти многогранников надо выбрать четыре, которые можно было бы сопоставить со стихиями. Какими соображениями руководствовался при этом Платон? Прежде всего тем, что некоторые элементы, как он считал, могли перейти друг в друга. Преобразование одних многогранников в другие могли быть осуществлены путем перестройки их внутренней структуры. Но для этого в данных телах нужно было найти такие структурные элементы, которые были бы для них общими. Из внешнего вида правильных многогранников явствует, что грани трех многогранников - тетраэдра, октаэдра, икосаэдра – имеют форму равностороннего треугольника. Два оставшихся многогранника – куб и додекаэдр – построены: первый - из квадратов, а второй - из правильных пятиугольников, поэтому они не могут преобразовываться ни друг в друга, ни в рассмотренные три тела. Это значит, что если мы придадим частицам трех стихий формы тетраэдра, октаэдра и икосаэдра, то частицы четвертой стихии будем считать кубами или додекаэдрами, но эта четвертая стихия не сможет переходить в три других, а всегда будет оставаться сама собой. Платон решил, что такой стихией может быть только земля и что мельчайшие частицы, из которых земля состоит, должны быть кубами. Тетраэдру, октаэдру и икосаэдру были сопоставлены соответственно огонь, воздух и вода.

Что касается пятого многогранника – додекаэдра, то он остается не у дел. По поводу него Платон ограничивается в «Тимее» замечанием, что «его бог определил для Вселенной и прибегнул к нему, когда разрисовывал ее и украшал».

Возникает вопрос «какими соображениями руководствовался Платон, приписывая частицам огня форму тетраэдра, частицам земли – форму куба и т.д.?». Здесь он учитывает чувственно-воспринимаемые свойства соответствующих стихий. Огонь – наиболее подвижная стихия, он обладает разрушительным действием, проникая в другие тела (сжигая или расплавляя, или испаряя их); при соприкосновении с ним мы испытываем чувство боли, как если бы мы укололись или порезались.

Какие частицы могли бы обусловить все эти свойства и действия? Очевидно, наиболее подвижные и легкие частицы, и притом обладающие режущими гранями и колющими углами. Из четырех многогранников, о которых может идти речь, в наибольшей степени удовлетворяет тетраэдр. Поэтому, говорит Платон, образ пирамиды (т.е. тетраэдра) и должен быть в согласии с правильным рассуждением и с правдоподобием, первоначалом и семенем огня (Тимей 56в). наоборот, земля выступает в нашем опыте как самая неподвижная и устойчивая из всех стихий. Поэтому частицы, из которых она состоит, должны иметь самые устойчивые основания. Из всех четырех тел этим свойством в максимальной мере обладает куб. Поэтому мы не нарушим правдоподобия, если припишем частицам земли кубическую форму (Тимей 56а). Аналогичным образом с двумя прочими стихиями мы соотнесем частицы, обладающие промежуточными свойствами. Икосаэдр, как самый обтекаемый, представляет частичку воды, октаэдр – частицу воздуха.

Пятый многогранник – додекаэдр – воплощал в себе «все сущее», символизировал весь мир и почитался главнейшим.

Мы видим, каким образом принцип правдоподобия сочетается у Платона с использованием данных повседневного опыта. Любопытно, что Платон почти не касается других, чисто спекулятивных, мотивов (например, связанных с теорией пропорций), которые играли решающую роль в построении его космологической концепции и которые могли оказать влияние и на некоторые аспекты его теории строения вещества.

Учитель.

Платон «правдоподобно» систематизировал картину мира. Это была одна из первых попыток ввести в науку саму идею систематизации, которая оказалась очень плодотворной. Она помогла отделить одни области знаний от других, сделав научные исследования более целенаправленными. Она сыграла выдающуюся роль и в отдельных науках, да, собственно говоря, во всех. Мы же воспользуемся самым наглядным примером, вспомнив о том, что значило для развития химии открытие периодической системы элементов Д.И. Менделеева. Термин «атом», употреблявшийся в Древней Греции, пережил тысячелетия, почти не изменив своего значения, а представления о геометрических формах мельчайших частиц возродились в форме кристаллов.

А теперь от Древней Греции перейдем к Европе XYI – XYII вв., когда жил и творил замечательный немецкий астроном, математик и великий фантазер Иоганн Кеплер (1571-1630).

Ученик.

Кеплер Иоганн (Kepler I,1571-1630г) – немецкий астроном. Открыл законы движения планет. В 1596 году Кеплер предложил правило, по которому вокруг сферы Земли описывается додекаэдр, а в нее вписывается икосаэдр. ( «Гармония мира» 1619г.)

И.Кеплер предположил, что расстояния между орбитами планет можно получить на основании Платоновых тел, вложенных друг в друга. Результаты его расчётов хорошо согласовались с действительными расстояниями между планетными орбитами

Весьма оригинальна космологическая гипотеза Кеплера, в которой он попытался связать некоторые свойства Солнечной системы со свойствами правильных многогранников. Кеплер предположил, что расстояния между шестью известными тогда планетами выражаются через размеры пяти правильных выпуклых многогранников (Платоновых тел). Между каждой парой "небесных сфер", по которым, согласно этой гипотезе, вращаются планеты, Кеплер вписал одно из Платоновых тел. Вокруг сферы Меркурия, ближайшей к Солнцу планеты, описан октаэдр. Этот октаэдр вписан в сферу Венеры, вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы - додекаэдр.

Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр. Вокруг тетраэдра описана сфера Юпитера, вписанная в куб. Наконец, вокруг куба описана сфера Сатурна. Эта модель выглядела для своего времени довольно правдоподобно. Во-первых, расстояния, вычисленные при помощи этой модели, были достаточно близки к истинным (учитывая доступную тогда точность измерения). Во-вторых, модель Кеплера давала объяснение, почему существует только шесть (именно столько было тогда известно) планет - именно шесть планет гармонировали с пятью Платоновыми телами.

Однако даже на тот момент эта привлекательная модель имела один существенный недостаток: сам же Кеплер показал, что планеты вращаются вокруг Солнца не по окружностям ("сферам"), а по эллипсам (первый закон Кеплера). Нечего и говорить, что позже, с открытием еще трех планет и более точным измерением расстояний, эта гипотеза была полностью отвергнута.

Другим выдающимся вкладом Кеплера в геометрию многогранников является открытие им двух звездных правильных тел. (Всего их четыре; два других нашел французский математик Луи Пуансон в 1809 г.)

Замечено, что наша матушка-Земля последовательно проходит эволюцию правильных объемных фигур. Существует много данных о сравнении структур и процессов Земли с вышеуказанными фигурами.

Полагают, что четырем геологическим эрам Земли соответствуют четыре силовых каркаса правильных Платоновских тел: Протозоа - тетраэдр (четыре плиты) Палеозою - гексаэдр (шесть плит) Мезозою - октаэдр (восемь плит) Кайнозою - додекаэдр (двенадцать плит).

С позиций изучения симметрии, учитывая представление о додекаэдро-икосаэдрическом силовом каркасе Земли как планеты, следует признать, что в этом смысле Земля является живым существом. С душою, которую П.А. Флоренский назвал “пневматосфера”, со свободой воли и разумом.

Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.

Учитель.

Рассуждая об устройстве мира, нельзя оставить без внимания живую природу. Встречаются ли в живой природе правильные многогранники?

Ученик.

Правильные многогранники встречаются и в живой природе. Например, скелет одноклеточного организма феодарии (Circogonia icosahedra) по форме напоминает икосаэдр. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное пытается себя защитить: из 12 вершин скелета выходят 12 полых игл. На концах игл находятся зубцы, делающие иглу еще более эффективной при защите.

Чем же вызвана такая природная геометризация феодарий? Тем, по-видимому, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объем при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.

Интересно, что икосаэдр оказался в центре внимания биологов в их спорах относительно формы некоторых вирусов. Вирус не может быть совершенно круглым, как считалось раньше. Для того чтобы определить его форму, брали разные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень – икосаэдр.

Правильные многогранники – самые выгодные фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов. Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она хорошо растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли (NaCl) имеют форму куба.

При производстве алюминия пользуются алюминиево-калиевыми квасцами (K[Al(SO4)2]·12H2O), монокристалл которых имеет форму правильного октаэдра.

Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра.

В разных химических реакциях применяется сурьменистый сернокислый натрий (Na5(SbO4(SO4)) – вещество, синтезированное учеными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.

Последний правильный многогранник – икосаэдр передает форму кристаллов бора (B). В свое время бор использовался для создания полупроводников первого поколения.

Итак, благодаря правильным многогранникам, открываются не только удивительные свойства геометрических фигур, но и пути познания природной гармонии.

Учитель.

Сегодня на уроке мы изучили правильные многогранники, рассмотрели их модели, выделили свойства каждого из многогранников. Кроме этого узнали, что правильные многогранники с древних времен привлекали внимание ученых, строителей, архитекторов и многих других. Их поражала красота, совершенство, гармония этих многогранников. Пифагорейцы считали эти многогранники божественными и использовали их в своих философских сочинениях о существе мира. Подробно описал свойства правильных многогранников древнегреческий ученый Платон. Правильным многогранникам посвящена последняя XIII книга знаменитых «Начал» Евклида. К многогранникам обращались и в более позднее время. Это видно из научных трудов Иоганна Кеплера.

К правильным многогранникам не были равнодушны скульпторы, архитекторы, художники. Слово предоставляется «искусствоведам».

Ученик.

В эпоху Возрождения большой интерес к формам правильных многогранников проявили художники. Леонардо да Винчи (1452-1519), например, увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал изображениями правильных и полуправильных многогранников книгу своего друга монаха Луки Пачоли (1445-1514) «О божественной пропорции».

Другим знаменитым художником эпохи Возрождения, увлекшимся геометрией, был Альбрехт Дюрер (1471-1528). В его известной гравюре «Меланхолия» на переднем плане изображен многогранник, гранями которого являются треугольники и пятиугольники. В 1525 году Дюрер написал трактат, в котором представил пять правильных многогранников, модели которых служат хорошими моделями перспективы.

При изучении творчества Сальвадора Дали увлекаешся его работой «Тайная вечеря». Это огромное полотно – подлинный шедевр живописи. Геометрический рационализм композиции свидетельствует о неодолимой вере в сакральную силу числа, спасительную совершенную форму, которая для художника олицетворяла духовную гармонию, нравственную чистоту и величие.

Обратите внимание на то, что вся сцена представлена на фоне правильного многогранника – додекаэдра. Я думаю, Сальвадор Дали был знаком с философской картиной мира Платона, который додекаэдру отводил особую роль – Вселенной. Поэтому не случайно изобразил данный многогранник, а чтобы показать всеобъемлемость Великой Троицы. То, что мы узнали о правильных многогранниках, позволит в дальнейшем обращать внимание на такие детали картин, в которые художник, оказывается, вкладывает особый смысл, передавая свое мировоззрение на устройство мира.

Посмотрите на гравюру Альбрехта Дюрера «Меланхолия». На ней изображен многогранник, причем наиболее четко видны грани-пятиугольники. Додекаэдр тоже имеет своими гранями пятиугольники. Нет ли здесь связи?

Читаем у Гете в «Фаусте»:

Мефистофель: Нет, трудновато выйти мне теперь,

Тут кое-что мешает мне немного:

Волшебный знак у вашего порога.

Фауст: Не пентаграмма ль этому виной?

Но как же, бес, пробрался ты за мной?

Каким путем впросак попал?

Мефистофель: Изволили ее вы плохо начертить,

И промежуток в уголку остался,

Там, у дверей, - и я свободно мог вскочить.

Пентаграмма – это звездчатый пятиугольник, который можно получить из правильного пятиугольника путем продолжения его сторон до взаимного пересечения. Оказалось, что у пифагорейцев пентаграмма была их отличительным знаком. Пентаграмме присваивалась способность защищать человека от злых духов.

Впрочем, многогранники - отнюдь не только объект научных исследований. Их формы - завершенные и причудливые, широко используются в декоративном искусстве.

Ярчайшим примером художественного изображения многогранников в XX веке являются, конечно, графические фантазии Маурица Эшера (1898-1972).

Мауриц Эшер в своих рисунках как бы открыл и интуитивно проиллюстрировал законы сочетания элементов симметрии, т.е. те законы, которые властвуют над кристаллами, определяя и их внешнюю форму, и их атомную структуру, и их физические свойства.

Математик, так же как и художник или поэт, создает узоры, и если его узоры более устойчивы, то лишь потому, что они составлены из идей.

Учитель.

Уважаемые, коллеги (ученики), я благодарю вас за ваш труд, труд исследователя. Все выступления, замечания, которые вы сделали на уроке, характеризуют вас как людей ищущих, творческих, талантливых, способных думать и выдвигать гипотезы, доказывать и слушать друг друга.

«Когда мы стремимся искать неведомое нам, то становимся лучше, мужественнее и деятельнее тех, кто полагает, будто неизвестное нельзя найти и незачем искать». Эта мысль Платона должна сопровождать вас на всем жизненном пути.

Таблица 1

Правильный многогранник	Число граней	Число вершин	Число ребер
Тетраэдр	4	4	6
Куб	6	8	12
Октаэдр	8	6	12
Додекаэдр	12	20	30
Икосаэдр	20	12	30

Таблица 2

Правильный многогранник	Сумма граней и вершин	Число ребер
Тетраэдр	4+4=8	6
Куб	6+8=14	12
Октаэдр	8+6=14	12
Додекаэдр	12+20=32	30
Икосаэдр	20+12=32	30

1.«Сумма числа граней и вершин равна числу ребер, увеличенному на 2»: Г + В = Р + 2.

2. Ребра правильного многогранника равны между собой.

3. Равны все двугранные углы, содержащие две грани с общим ребром. Следовательно, радиус вписанной и описанной сферы многогранника совпадают.

Таблица 3

Правильный многогранник	Радиус описанной сферы	Радиус вписанной сферы	Площадь поверхности
Тетраэдр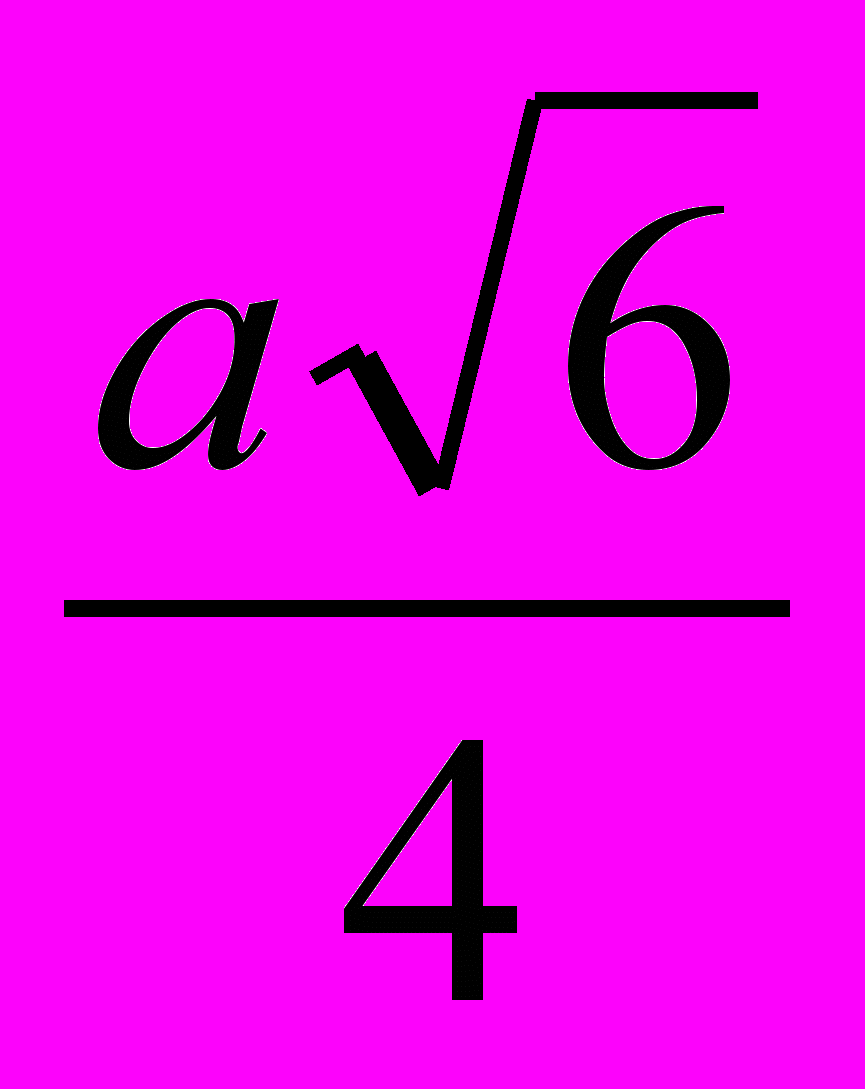
Куб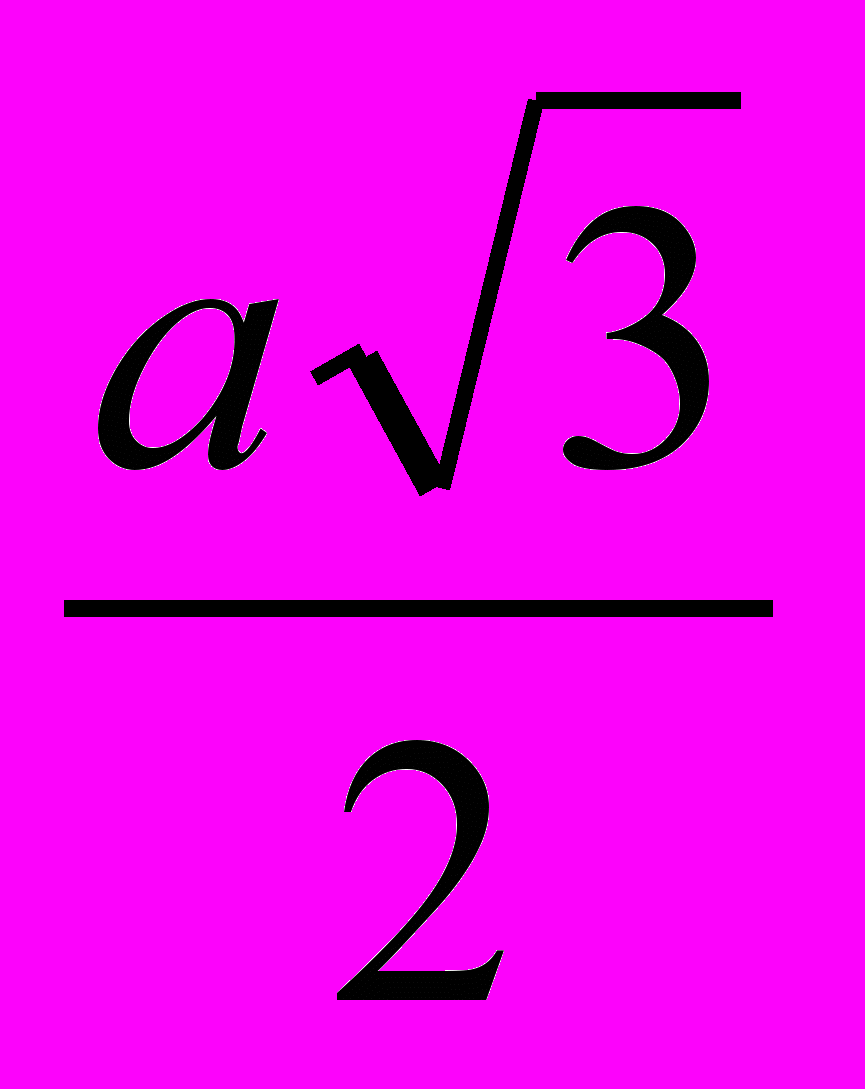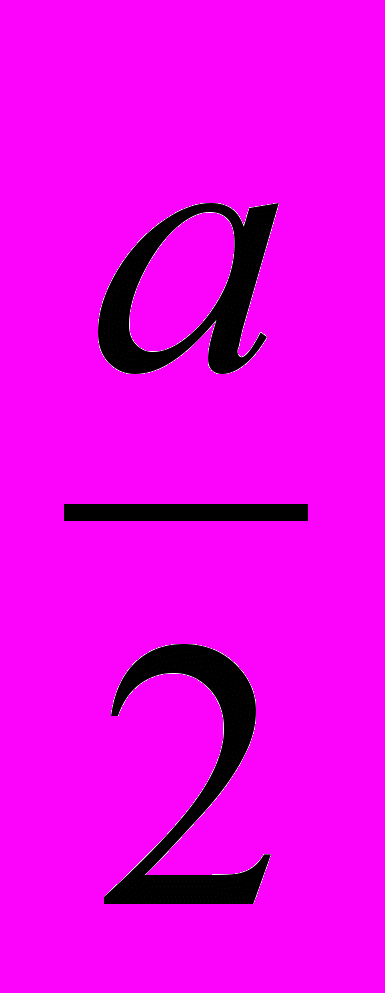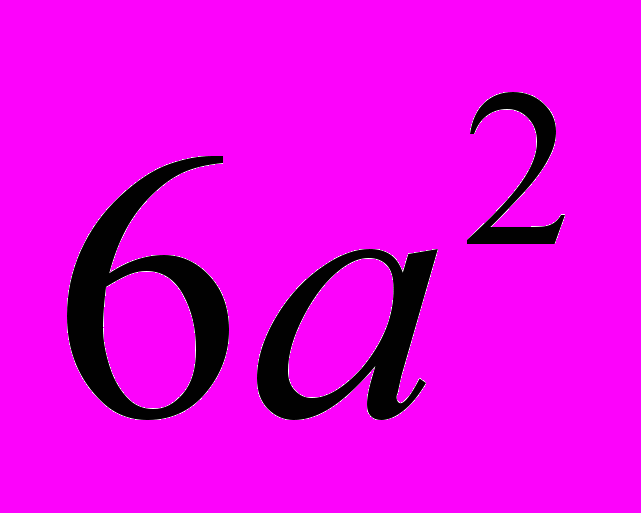
Октаэдр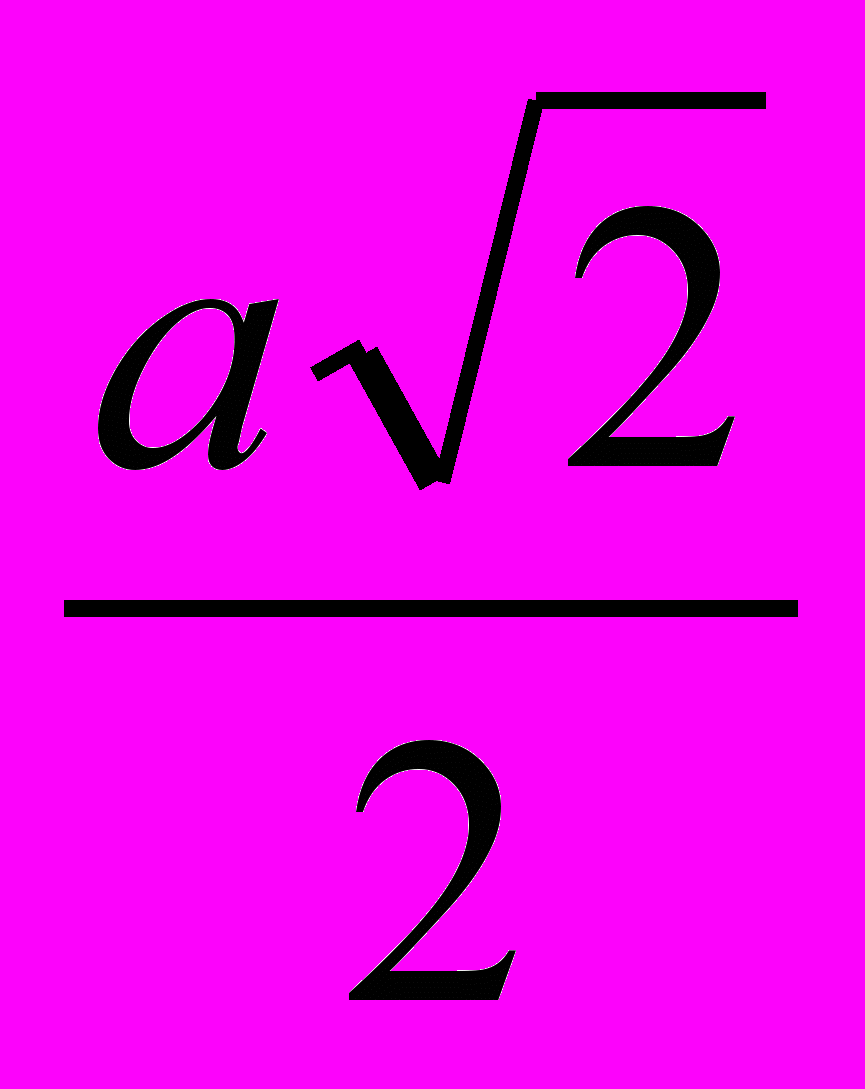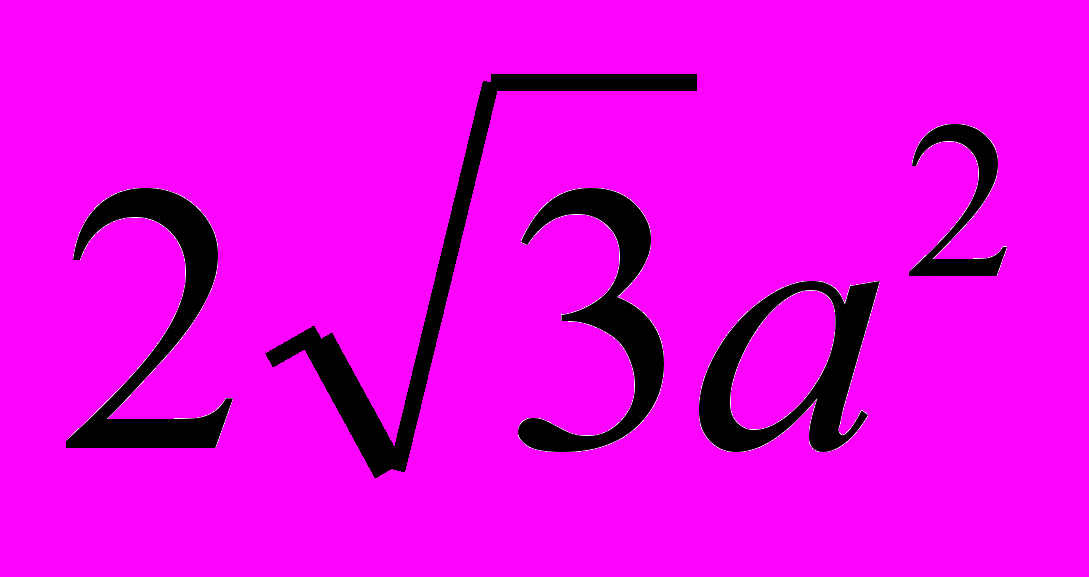
Додекаэдр		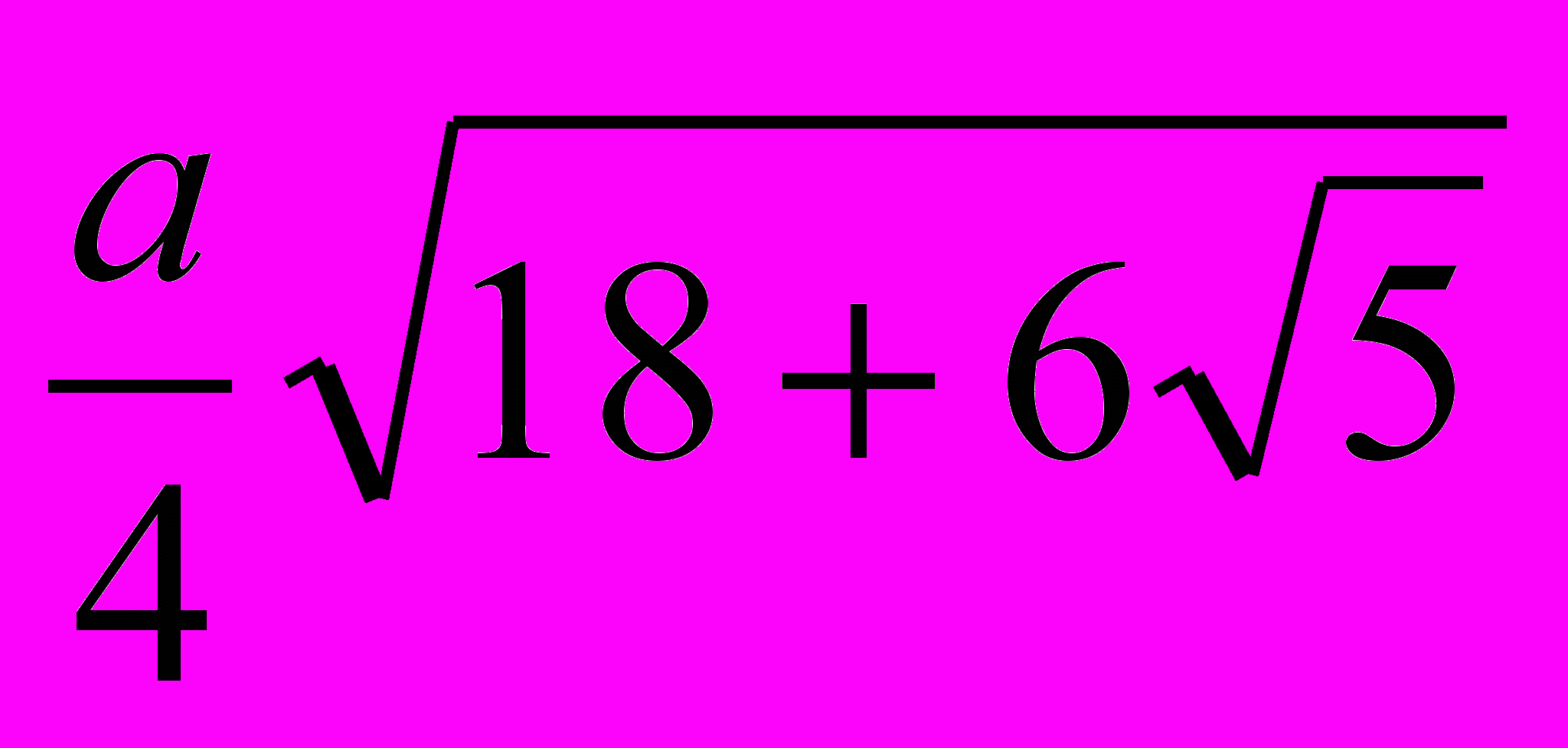	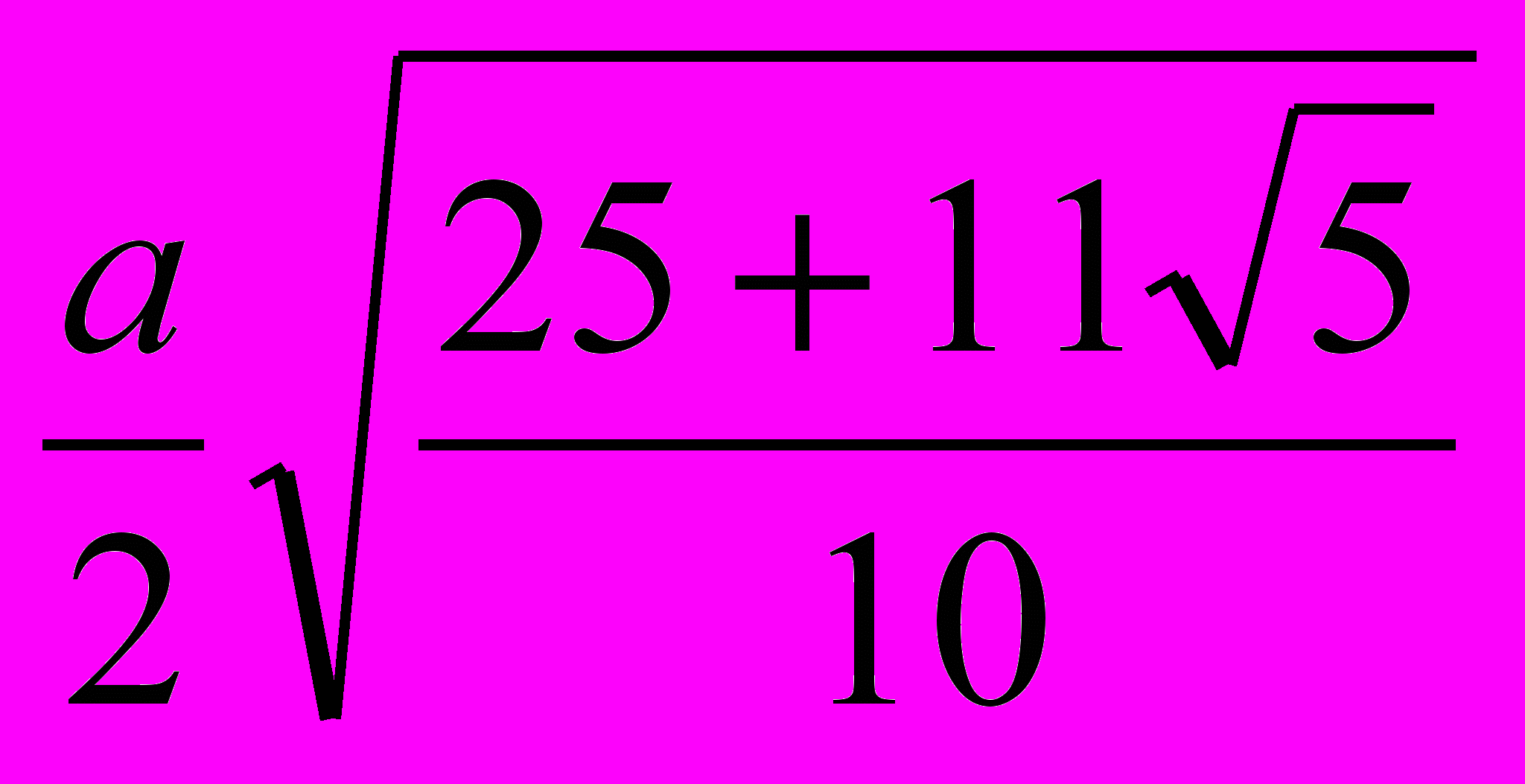3
Икосаэдр		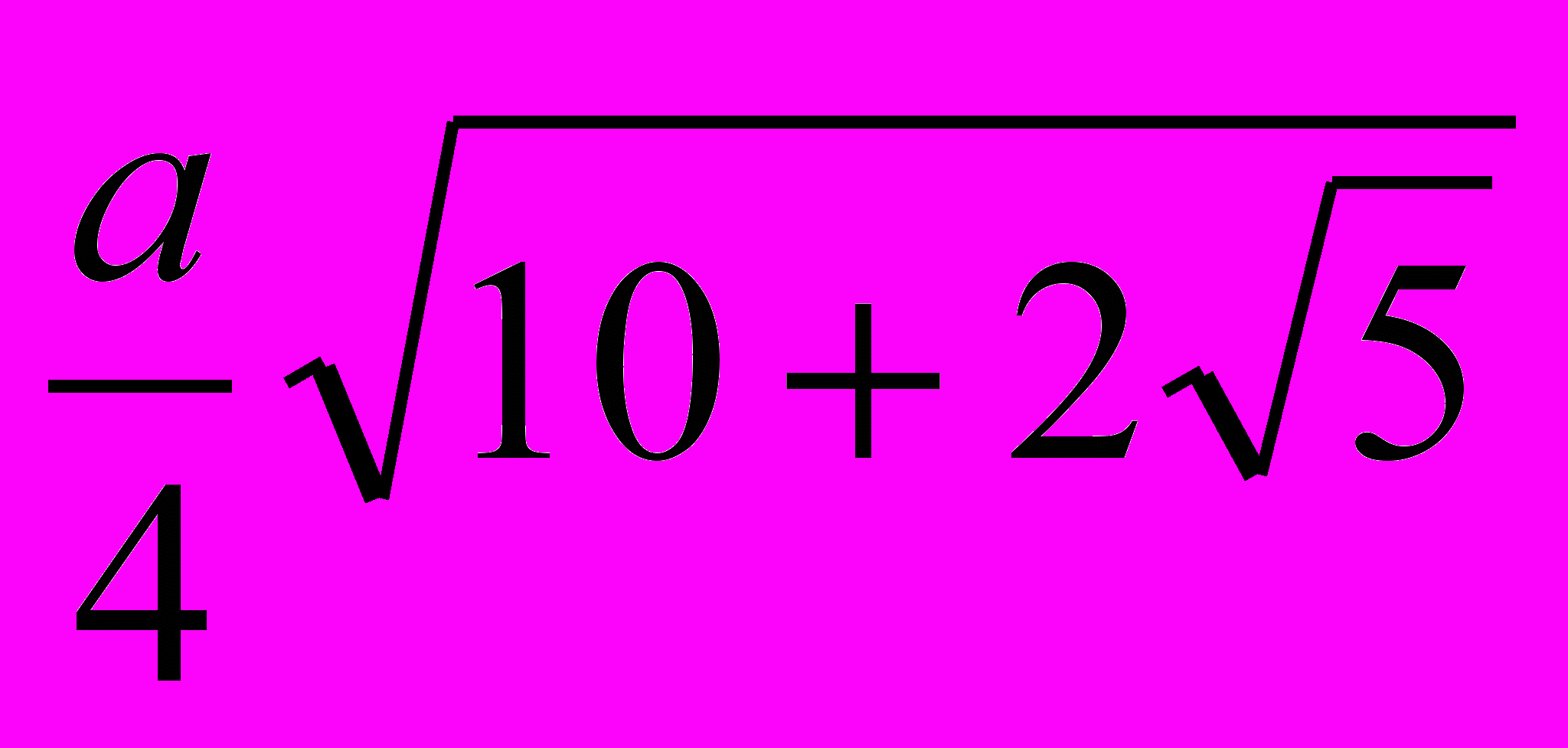	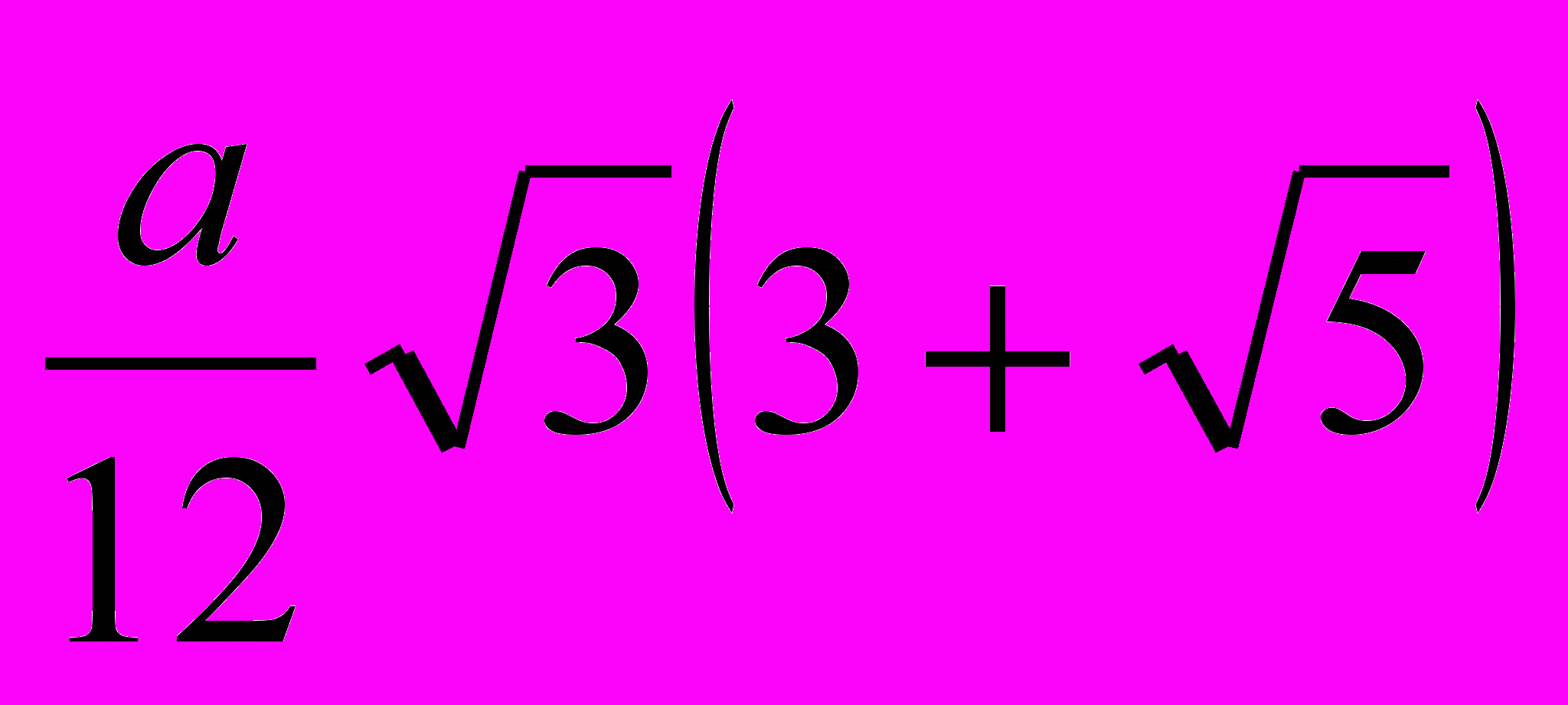5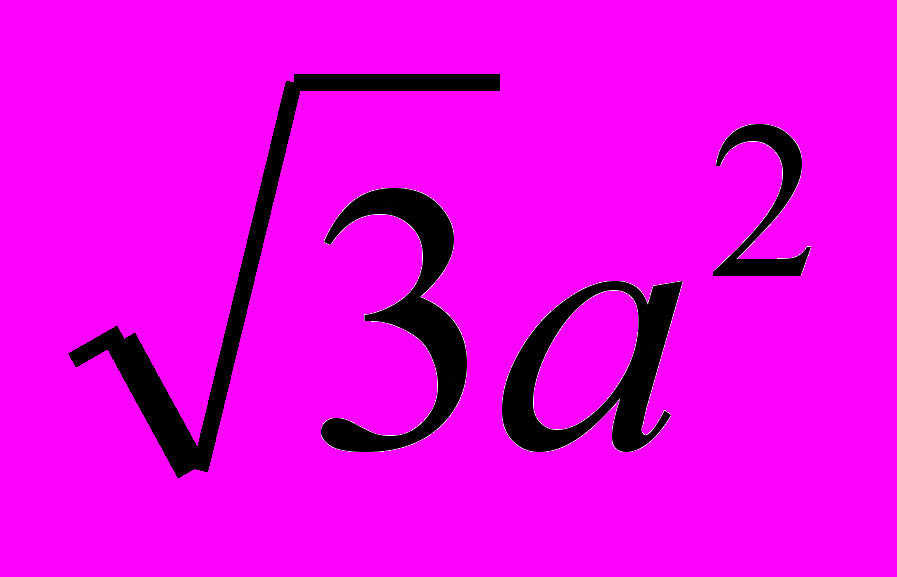

Сначала рассмотрим случай, когда грани многогранника - равносторонние треугольники. Поскольку внутренний угол равностороннего треугольника равен 60°, три таких угла дадут в развертке 180°. Если теперь склеить развертку в многогранный угол, получится тетраэдр - многогранник, в каждой вершине которого встречаются три правильные треугольные грани. Если добавить к развертке вершины еще один треугольник, в сумме получится 240°. Это развертка вершины октаэдра. Добавление пятого треугольника даст угол 300° - мы получаем развертку вершины икосаэдра. Если же добавить еще один, шестой треугольник, сумма углов станет равной 360° - эта развертка, очевидно, не может соответствовать ни одному выпуклому многограннику. Теперь перейдем к квадратным граням. Развертка из трех квадратных граней имеет угол 3x90°=270° - получается вершина куба, который также называют гексаэдром. Добавление еще одного квадрата увеличит угол до 360° - этой развертке уже не соответствует никакой выпуклый многогранник. Три пятиугольные грани дают угол развертки 3*108°=324° - вершина додекаэдра. Если добавить еще один пятиугольник, получим больше 360°. Для шестиугольников уже три грани дают угол развертки 3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует. Таким образом, мы убедились, что существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями.

Тест.

Какие многогранники называются правильными.
1. Выпуклый многогранник называется правильным, если все его грани – правильные многоугольники.
2. Выпуклый многогранник называется правильным, если все его грани – правильные многоугольники и в каждой его вершине сходится одно и то же число ребер
3. Выпуклый многогранник называется правильным, если в основании лежит правильный многоугольник и основание высоты совпадает с центром многогранника
Апофема это -
1. Высота призмы
2. Высота основания пирамиды
3. Высота боковой грани.
Сколько у тетраэдра граней, ребер, вершин
1. Г-4 Р-4 В-6
2. Г-4 Р-6 В-4
3. Г-6 Р-4 В-4
Ребро куба 2 см. Чему равна площадь полной поверхности.
1. 24
2. 16
3. 48
Площадь боковой поверхности прямой призмы равна
1. периметр основания на апофему
2. полупериметр основания на высоту
3. Периметр основания на высоту.
Могут ли все грани треугольной пирамиды быть прямоугольными треугольниками?
1. Да
2. Нет
На какие многогранники рассекает треугольную призму плоскость, проходящая через вершину верхнего основания и противоположную ей сторону нижнего основания?
1. треугольную и четырехугольную пирамиды.
2. две треугольные призмы.
3. две треугольные пирамиды.
Космонавт сообщил на базу, что обнаружил странный космический объект. Это геометрически правильное твердое тело, которое выглядит одинаково, какой бы гранью ни повернулось. Так было до тех пор, пока космонавт до него не дотронулся. После чего три грани космического тела пульсируют красными огнями, три - голубыми, а остальные шесть - зелеными. Ученые на базе до сих пор пытаются определить, что это за огни. Однако теперь они знают форму всех граней космического объекта. А вы знаете?
1. Икосаэдр
2. Додекаэдр
3. архимедово тело

Blog

Урок на семинаре: «Правильные многогранники»