А. В. Попов 1/2 года, 3-5 курс Закон
| Вид материала | Закон |
- С. В. Попов Введение в методологию март 1992 года, Мытищи Попов , 622.83kb.
- Попов Александр Степанович, 20.54kb.
- Попов В. И. Современная дипломатия: теория и практика. Дипломатия наука и искусство:, 192.98kb.
- Александр Попов, 2451.05kb.
- Биография Александр Степанович Попов родился в на в посёлке, 294.81kb.
- Современные русские писатели евгений Попов Рассказы, 246.11kb.
- Методические указания по эксплуатации газового хозяйства тепловых электростанций, 1550.75kb.
- Александр Степанович Попов. Датой изобретения радио принято считать 7 мая 1895 г.,, 74.6kb.
- Б. И. Вершинин Л. Е. Попов С. Н. Постников, 4094.28kb.
- Курс с приоритетом самостоятельной работы студентов (с 2004 года). Модульный кур, 28kb.
РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ КВАЗИЛИНЕЙНЫХ УРАВНЕНИЙ
доц. А.В. Попов
1/2 года, 3-5 курс
1. Законы сохранения в МСС. Интегральная и дифференциальная форма их записи. Математические модели вязкого и невязкого газа, идеальной и вязкой жидкости. Примеры постановок начально-краевых задач.
2. Понятия сходимости, аппроксимации и устойчивости в теории р.с. Теорема Филиппова (о связи между сходимостью, аппроксимацией и устойчивостью). Теорема Куранта (об областях зависимости), спектральный признак устойчивости (СПУ).
3. Простейшие явные разностные схемы для уравнения переноса (с односторонними разностями, центральной разностью по пространственной переменной, схема Лакса). Исследование их свойств по теореме Куранта и СПУ.
4. Дифференциальное приближение разностной схемы. Эвристический анализ разностных схем на основе дифференциального приближения. Дисперсионные и диссипативные свойства р.с.
5. Разностные схемы Лакса-Вендрофа, "крест", как примеры разностных схем второго порядка точности. Их свойства. Пример исследования р.с. "крест" для системы уравнений акустики по СПУ.
6. Р.с. с весами для уравнения переноса. Погрешность аппроксимации. Исследование энергетическим методом устойчивости р.с. с весами в норме
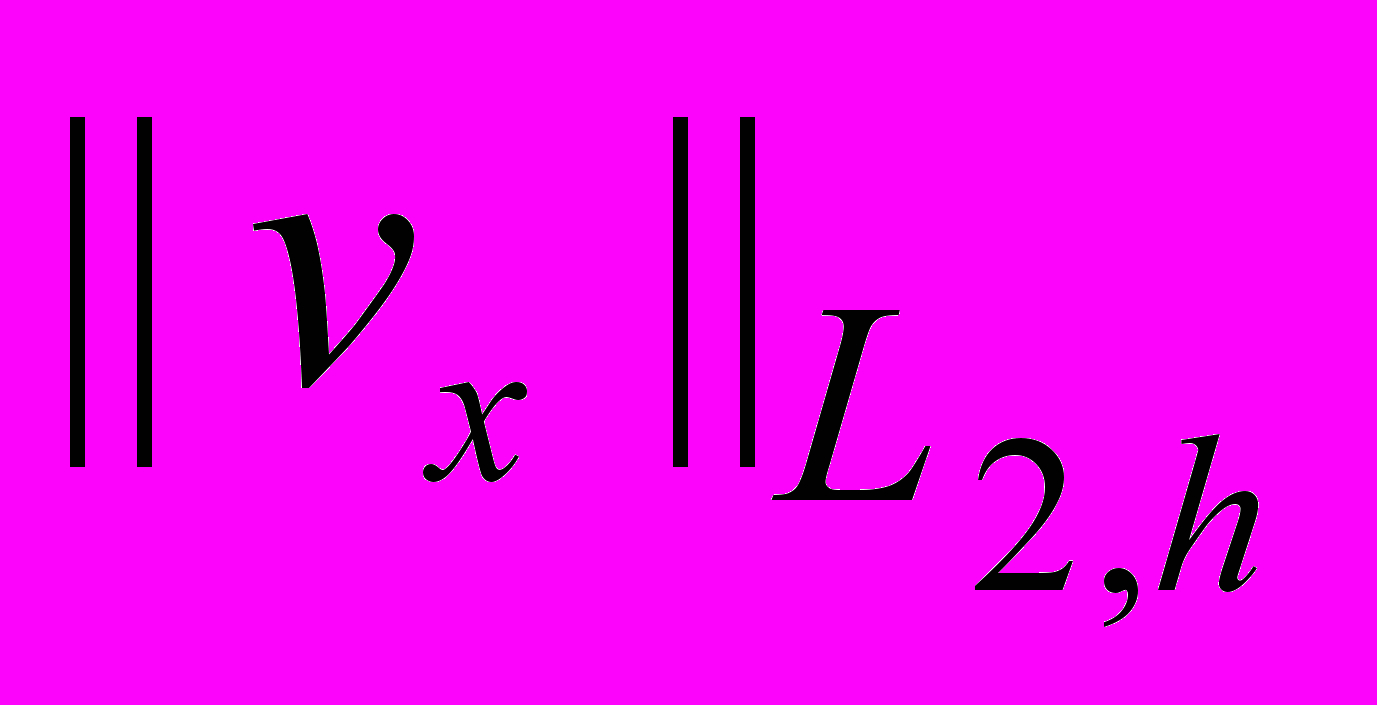.7. Операторно-разностная форма записи р.с. Достаточные условия устойчивости р.с. в ЛНП. Оператор перехода. Энергетическое тождество для двухслойных разностных схем. Необходимое и достаточное условие устойчивости р.с. в
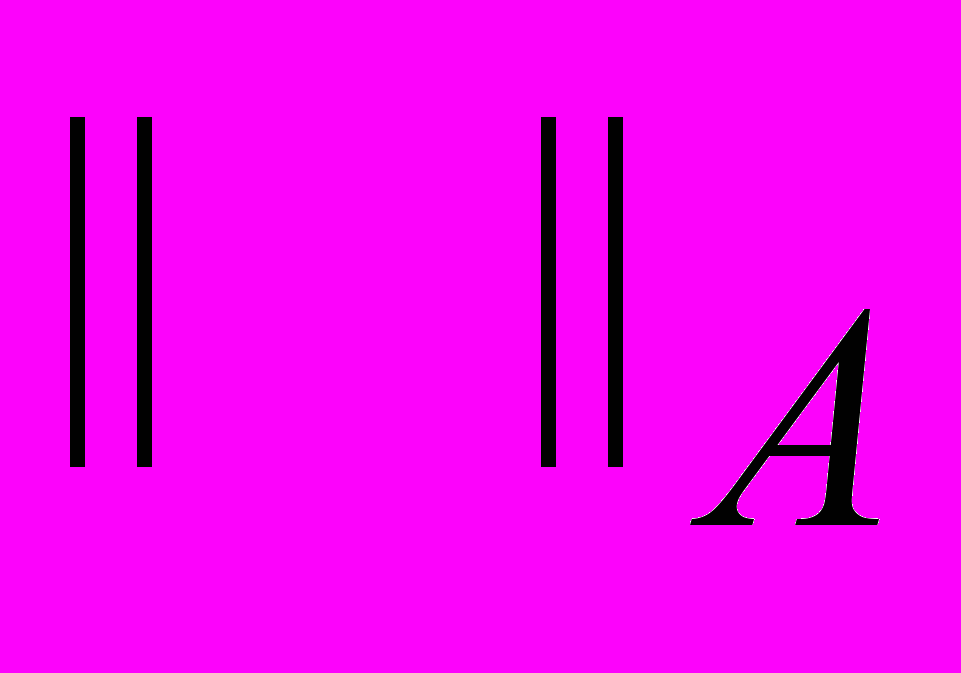. Примеры исследования устойчивости р.с. с весами в операторно-разностной форме для уравнения переноса и теплопроводности. Априорные оценки устойчивости р.с. по правой части.8. Численное решение задач с негладкими данными.
9. Задача Коши для одного квазилинейного уравнения первого порядка. Характеристическая система. Геометрическая интерпретация решения. Точное решение задачи Коши для невязкого уравнения Бюргерса с кусочно-линейной начальной функцией. Понятие слабого решения. Условия Гюгонио на разрыве. Волны сжатия и разрежения.
10. Явная разностная схема для решения линейного вязкого уравнения Бюргерса. Ее дифференциальное приближение. Исследование устойчивости по СПУ. Сеточное число Рейнольдса. Модификации р.с. с улучшенными дисперсионными свойствами. Неявная разностная схема для линейного вязкого уравнения Бюргерса. Существование и единственность ее решения. Исследование устойчивости энергетическим методом для
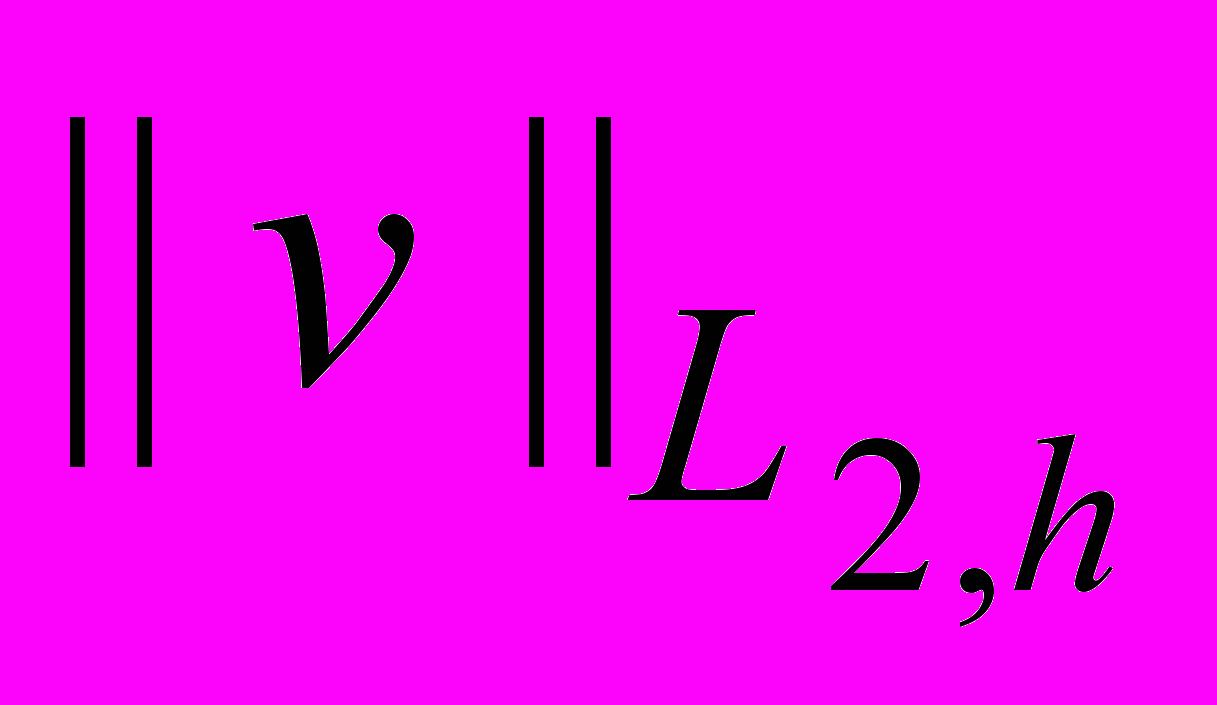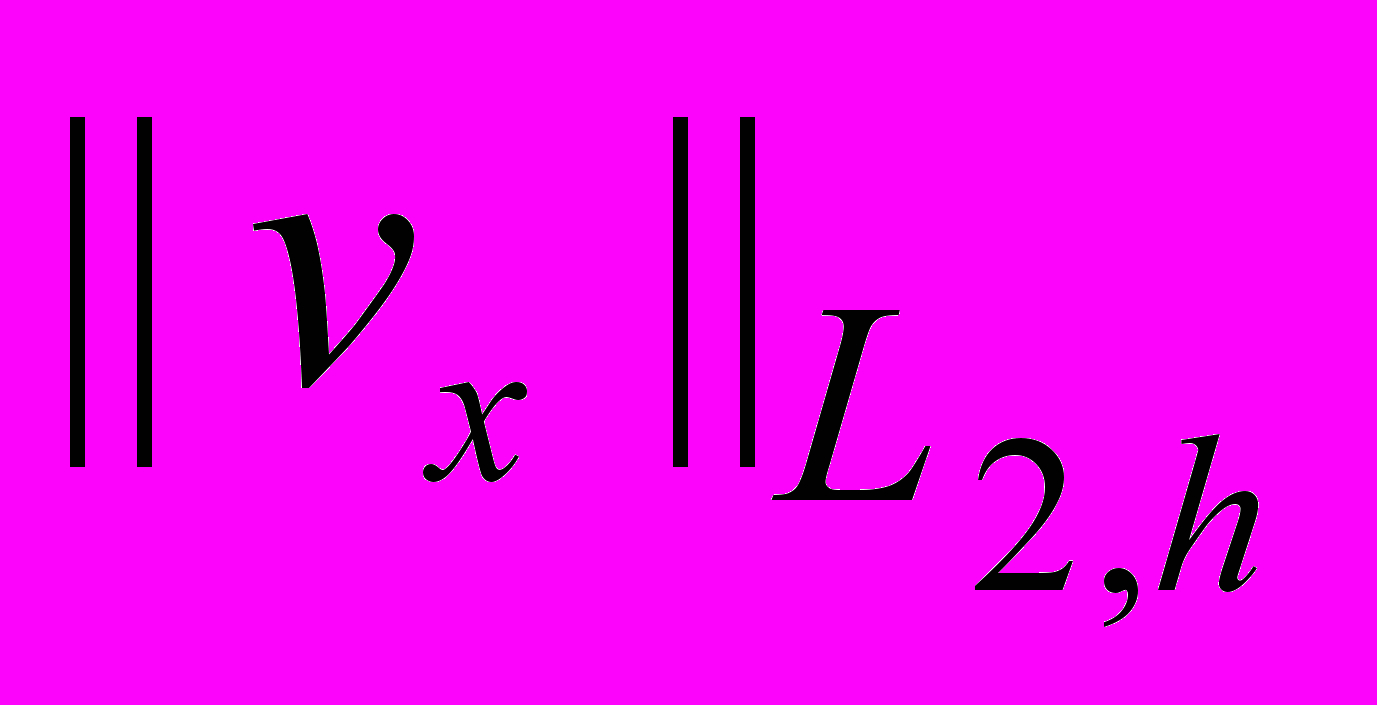и . Неявная разностная схема для нелинейного вязкого уравнения Бюргерса. Кососимметричность оператора, аппроксимирующего конвективную часть дифференциального оператора. Оценки погрешности численного интегрирования в нормах 
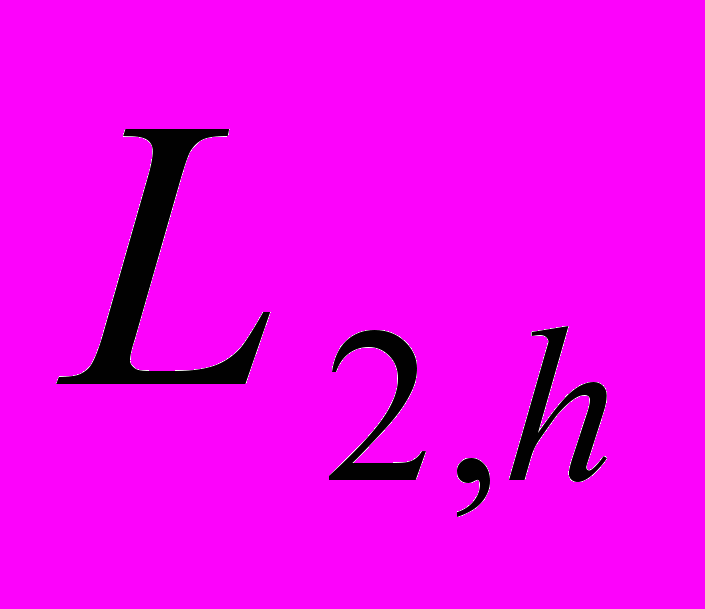и 
.11. Экономичные разностные схемы решения двумерных нестационарных задач.
Литература
1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М., Лаборатория базовых знаний, 2000.
2. Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений и их приложения к газовой динамике. М., Наука, 1978.
3. Самарский А.А. Теория разностных схем. М., Наука, 1983.
4. Андерсон Д., Таннехил Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен. Т. 1. М., Мир, 1990.
5. Бахвалов Н.С. Численное решение задач с негладкими данными и интеполяционные теоремы.// Труды МИ АН СССР, 1984, т. 166, с. 18-22.
6. Антонцев, Кажихов, Монахов. Краевые задачи механики жидкостей и газов. Новосибирск, Наука, 1983.
7. Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. М., Наука, 1980.
8. Годунов С.К., Рябенький В.С. Разностные схемы. М., Наука, 1977.
9. Бахвалов Н.С. О накоплении вычислительной погрешности при численном решении дифференциальных уравнений.// Сб. работ ВЦ МГУ, 1962, № 1. c. 47-68.
10. Попов А.В. Практикум на ЭВМ. Разностные методы решения квазилинейных уравнений первого порядка. М., изд-во ЦПИ при мех-мат. ф-те МГУ, 1999.
11. Горицкий А.Ю., Кружков С.Н., Чечкин Г.А. Уравнения с частными производными первого порядка. (Учебное пособие) М., изд-во ЦПИ при мех-мат. ф-те МГУ, 1999.
12. Попов А.В. Неявные разностные схемы для нестационарного движения вязкого газа. Труды математического центра имени Н.И. Лобачевского. Т. 13. Численные методы решения линейных и нелинейных краевых задач. Материалы всероссийской молодежной научной школы-конференции (Казань, 19-23 ноября 2001 г.). Казань, изд-во "ДАС". 2001, с. 4-54.