Ая турбулентность, перенос излучения, тепла, пыли и реагирующих газов, динамику водяного пара и капель, конденсацию и испарение капель, поглощение газов каплями

Вид материала

Документы

Подобный материал:

• Математическая модель микроклимата в производственных помещениях с повышенной влажностью, 60.26kb.
• Атмосферный воздух всегда содержит некоторое количество влаги в виде водяного пара, 9.38kb.
• Название Исследование сезонной изменчивости потоков углекислого газа, метана и водяного, 107.54kb.
• Цель работы графическое определение параметров влажного воздуха, 173.3kb.
• Примерная программа дисциплины теория процессов и аппаратов очиски газов, 85.96kb.
• Методика расчета выбросов парниковых газов Содержание, 1290.76kb.
• О. Н. Сидорчук, магистр., А. П. Мартыненко, ст преп, 71.29kb.
• *в хогвартсе расцветала весна и даже шумная капель не беспокоила ребят, 428.77kb.
• Технологии производства технических газов, 110.26kb.
• Программа учебной дисциплины «Кинетическая теория неравновесных смесей газов» специальность, 118.5kb.

В.В. Пекунов


Ивановский государственный энергетический университет (г. Иваново)

Региональный НОЦ по наноматериалам «Жидкие кристаллы» (г. Иваново)


МОДЕЛЬ ОБРАЗОВАНИЯ И РАСПРОСТРАНЕНИЯ ЗАГРЯЗНЕНИЙ

С УЧЕТОМ ИЗЛУЧЕНИЯ И МЕЖФАЗНЫХ ПЕРЕХОДОВ


Предлагается трехмерная многофазная модель образования и распространения загрязнений, учитывающая турбулентность, перенос излучения, тепла, пыли и реагирующих газов, динамику водяного пара и капель, конденсацию и испарение капель, поглощение газов каплями. Введем правую систему координат (x₁, x₂, x₃) с вертикальной осью Ox₃.

; j = 1, 2, 3;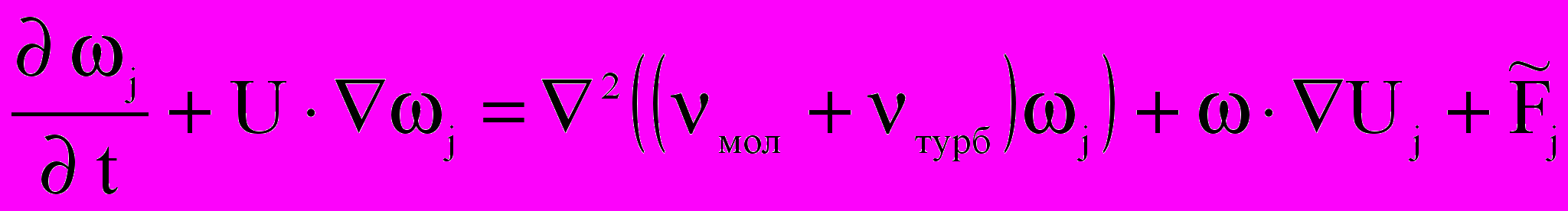

; j = 1, 2, 3;

; ; ;

,

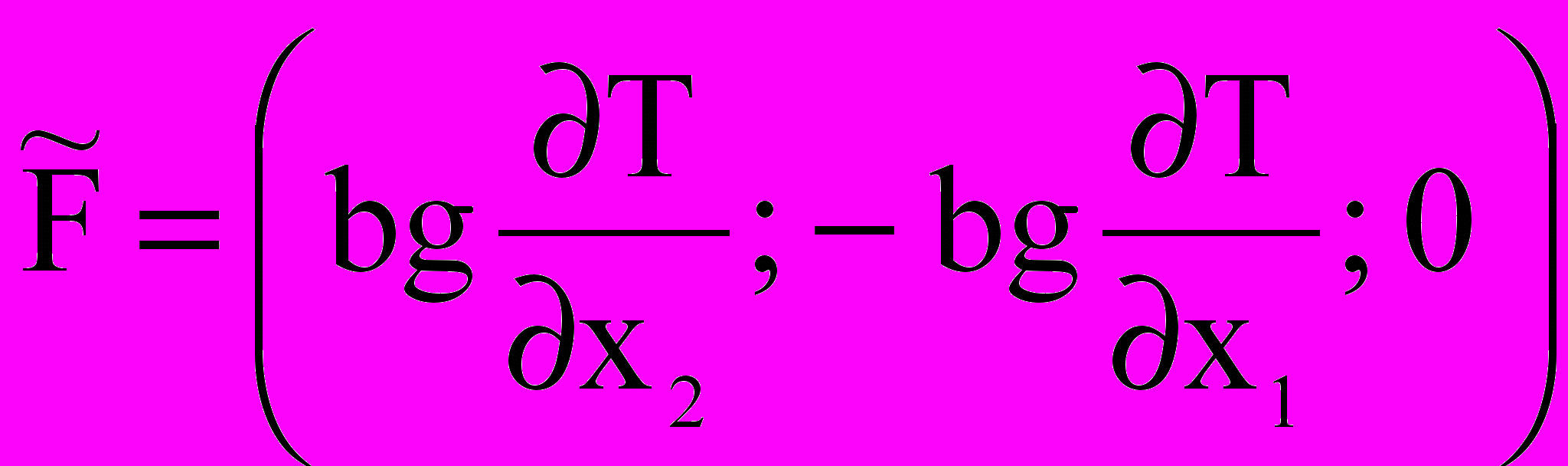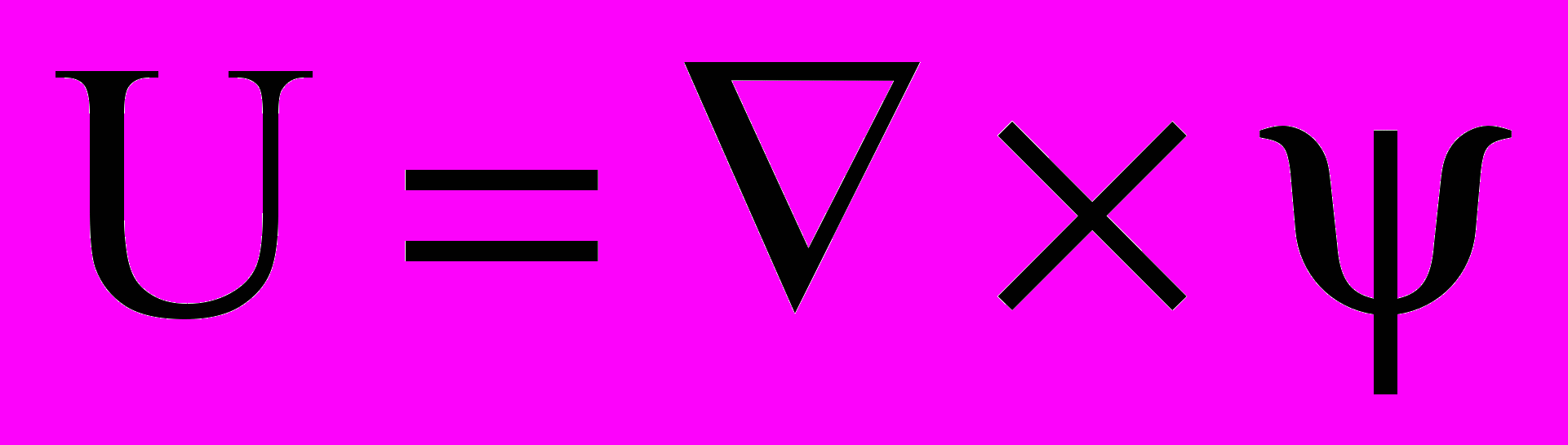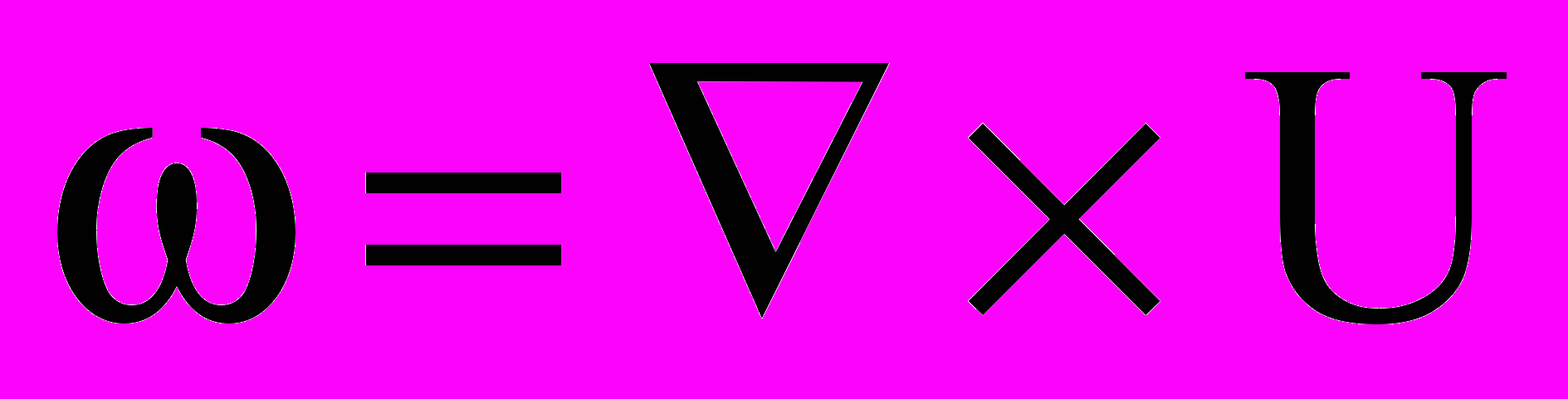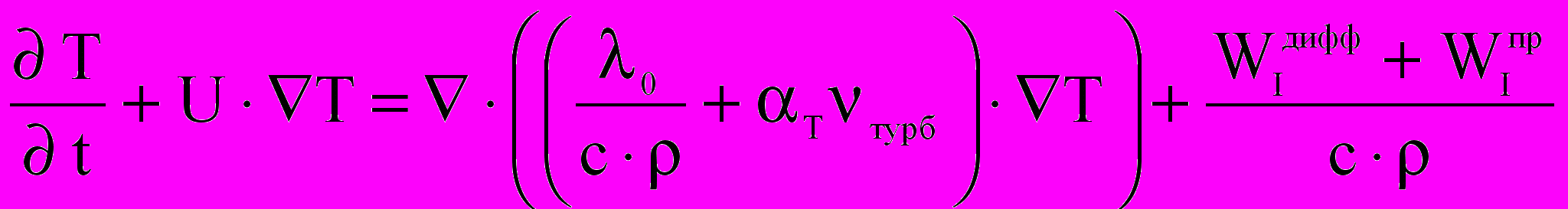где  — векторный потенциал,  — вектор вихря, U — вектор скорости основной фазы, _мол и _турб — молекулярная и турбулентная вязкости, T — температура, ₀, c, , b — теплопроводность, удельная теплоемкость, плотность и термический коэффициент расширения воздуха,  —коэффициенты. Модель турбулентности Абрамовича-Секундова:

;

; ; ,

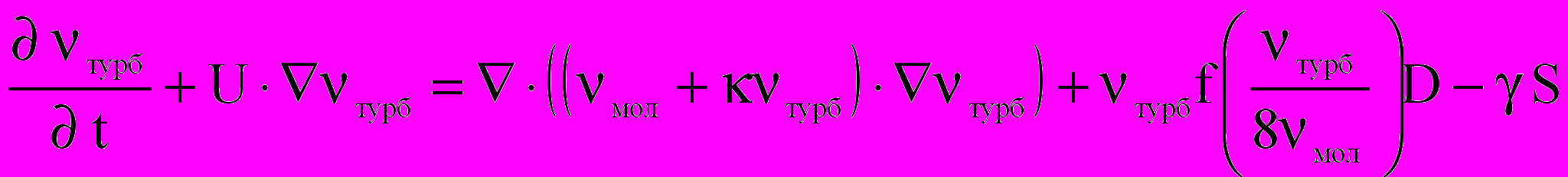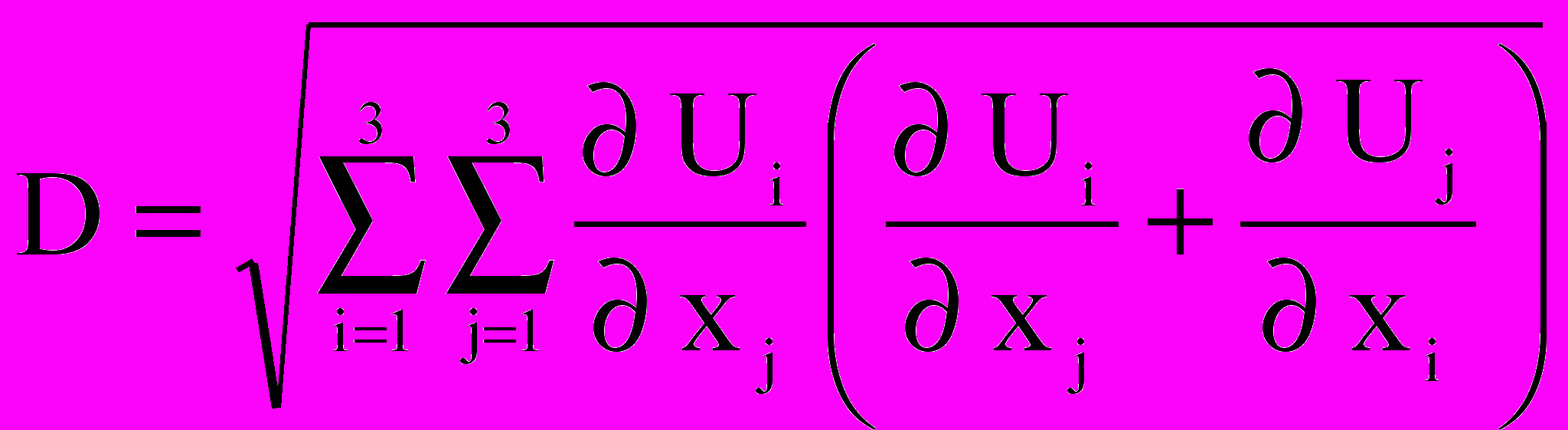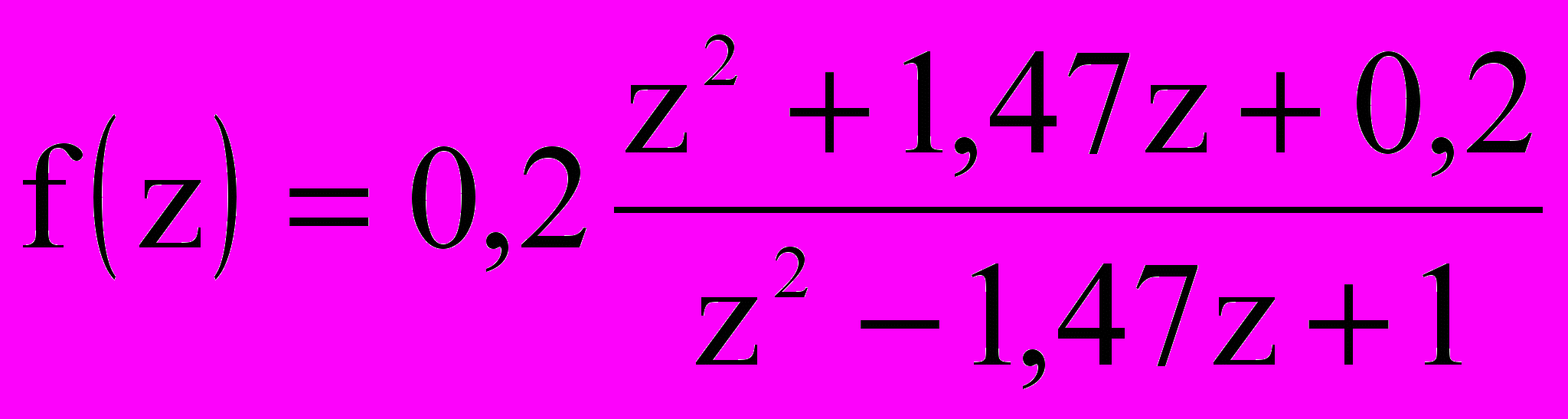где  = 2,0,  = 50,0,  = 0,06, L_min — кратчайшее расстояние до стенки.

;

;

; ,

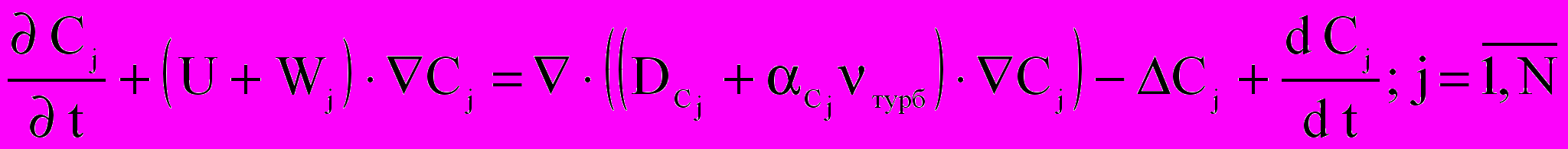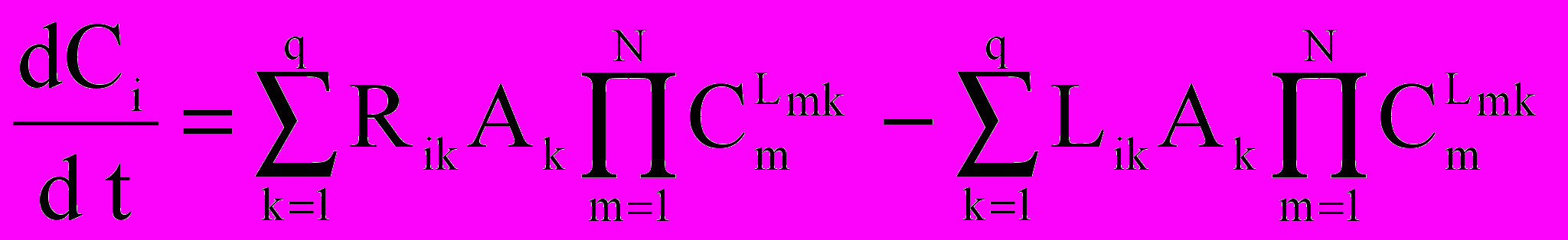где C — вектор концентраций веществ (газов и переносимых воздухом пылевых частиц), W_j, 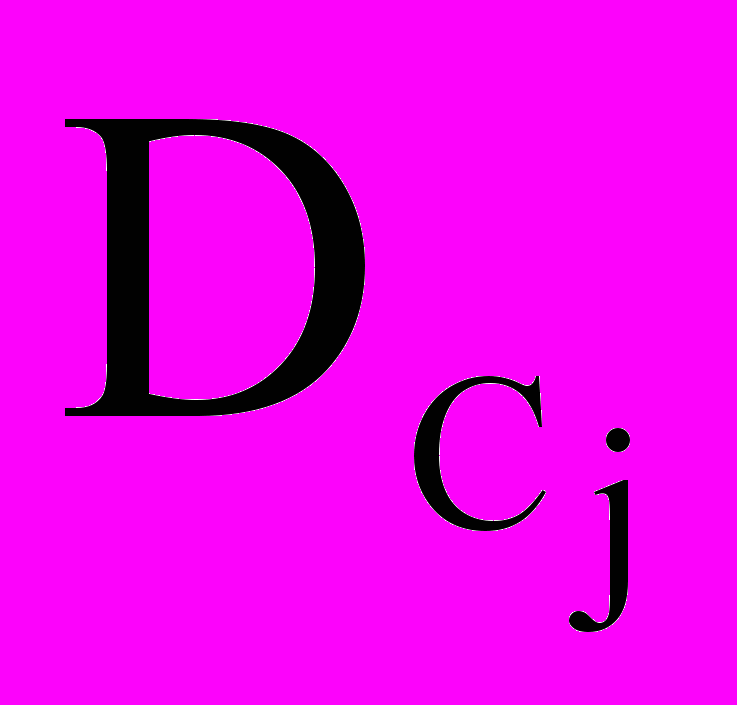— скорость витания и коэффициент диффузии j го вещества, N — число веществ, q — число химических реакций, R_ik и L_ik — стехиометрические коэффициенты при i-м веществе в правой и левой частях k-й реакции, A_k = A_k(T) — константа скорости k-й реакции. Для фотохимических реакций A_k отлична от нуля лишь в случае, если суммарная освещенность превышает заданный стартовый порог.

Особо выделим уравнение диффузии пара с концентрацией :

;

,

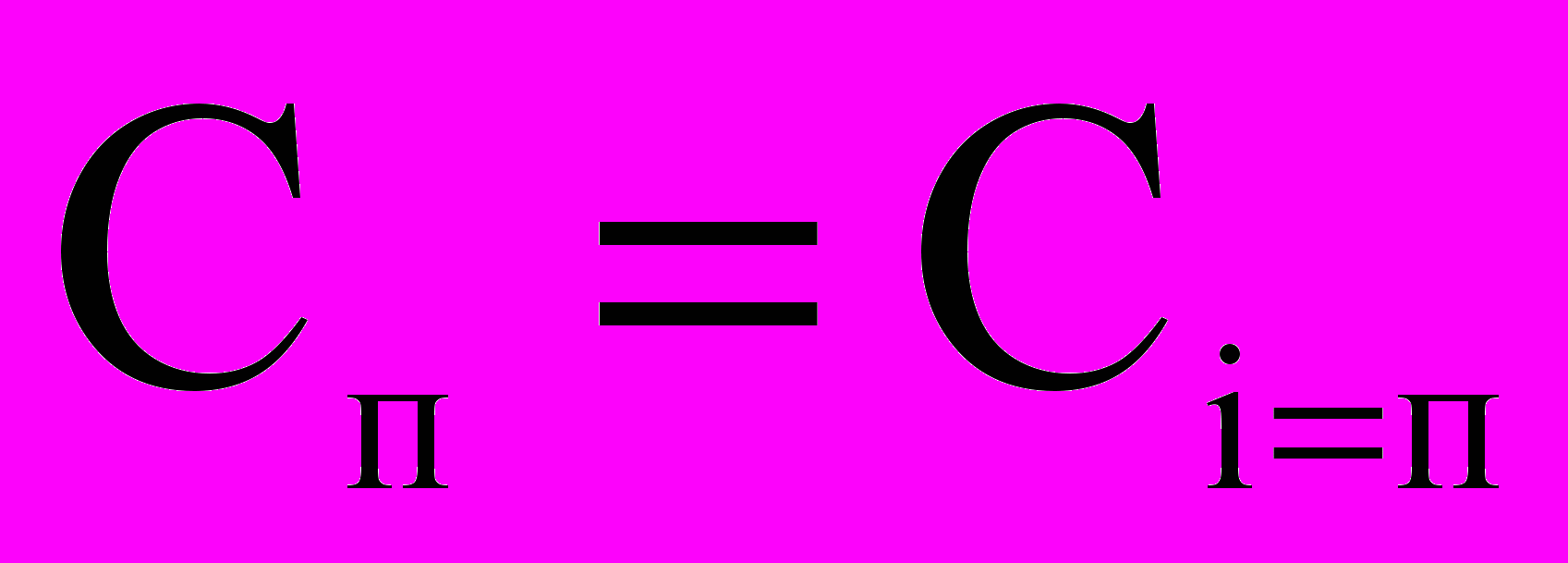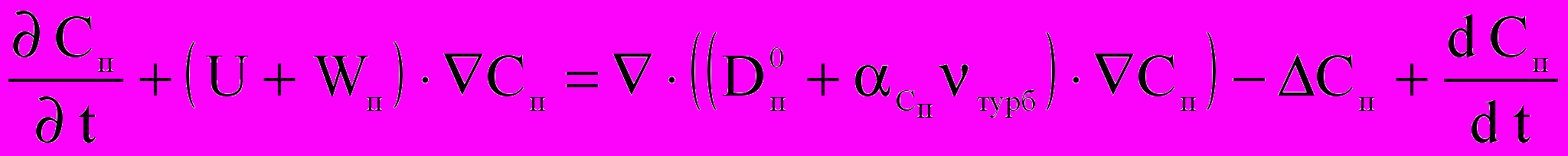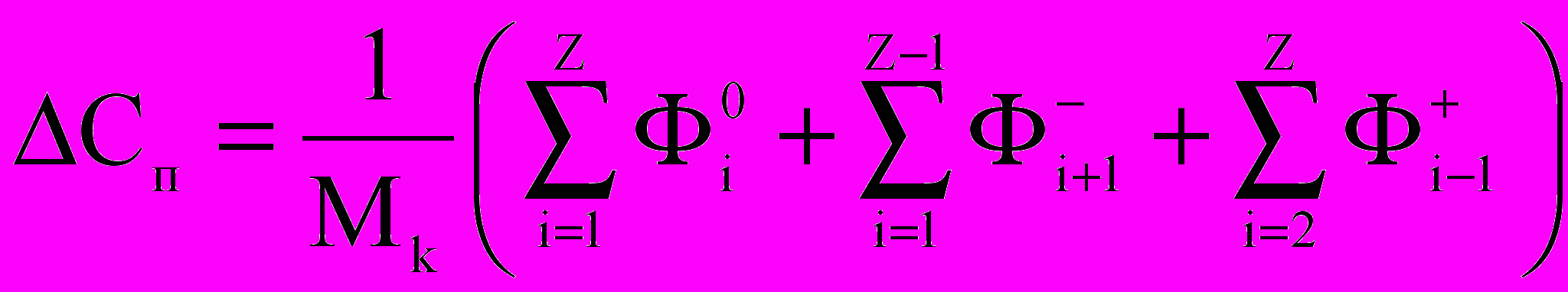где 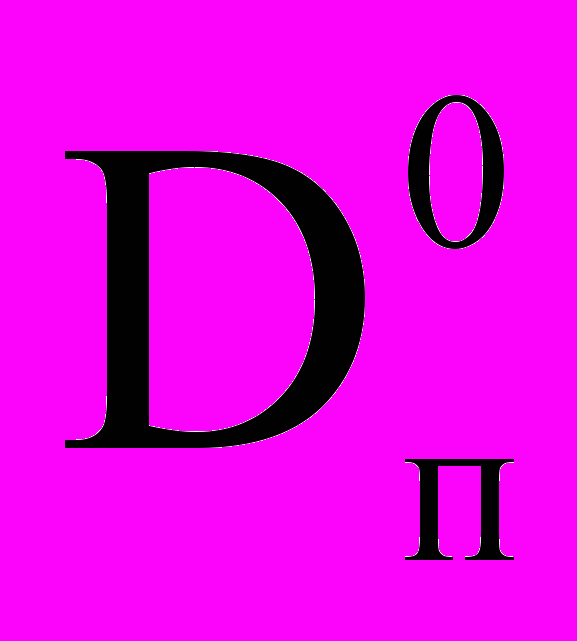— коэффициент диффузии пара, M_k — молярная масса воды. Уравнения переноса диффузного излучения в N_rad диапазонах (в последнем диапазоне — тепловое инфракрасное излучение) по модели K.N.Liou:

; ;



; ,

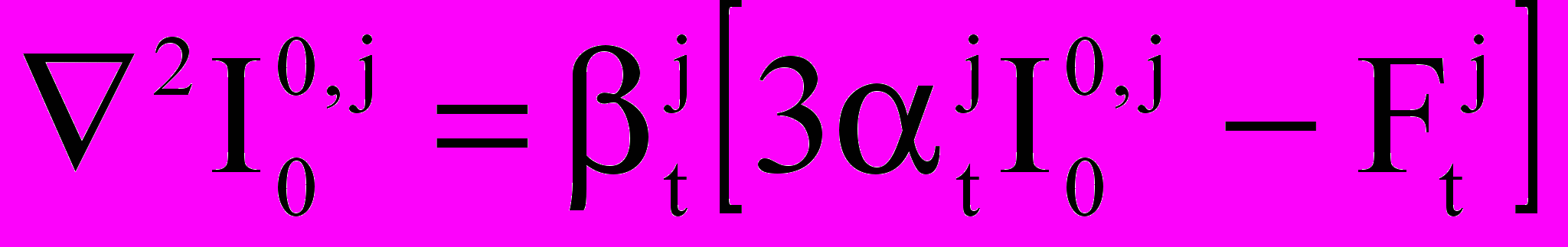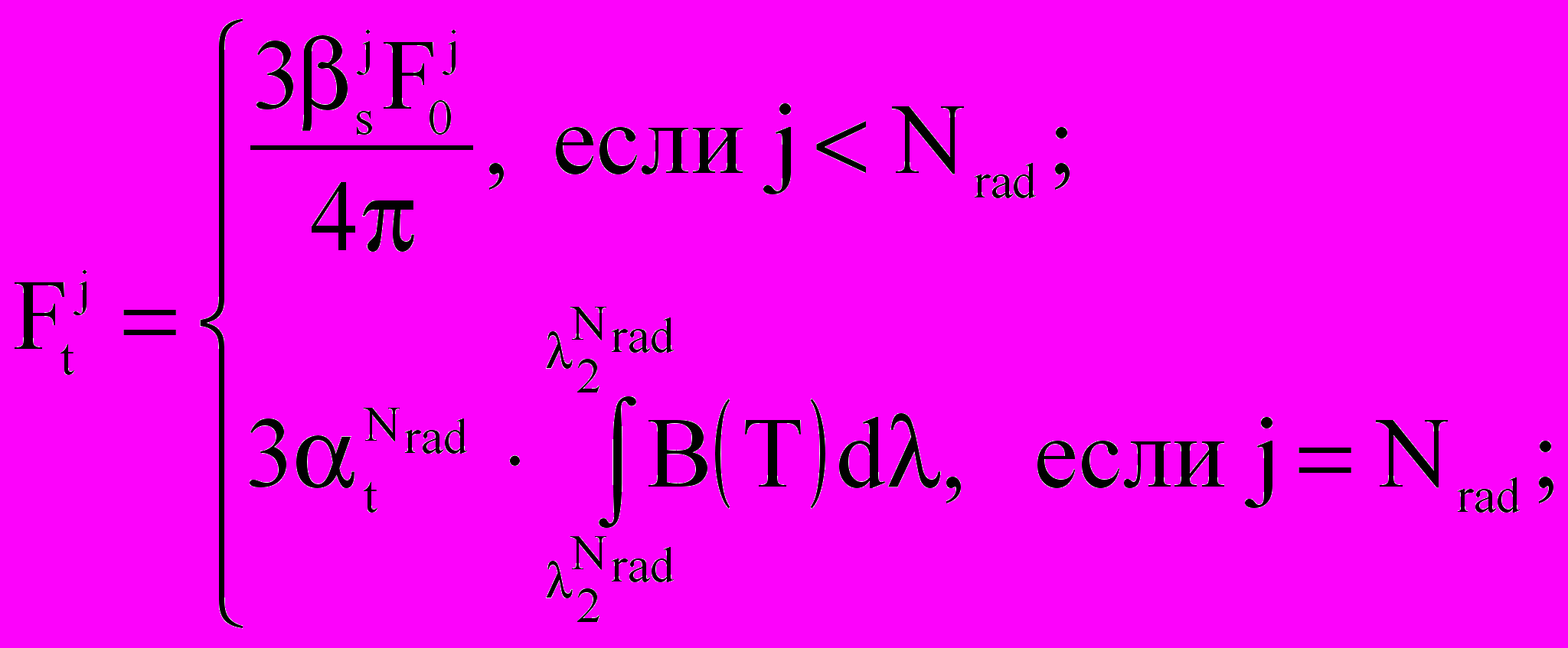
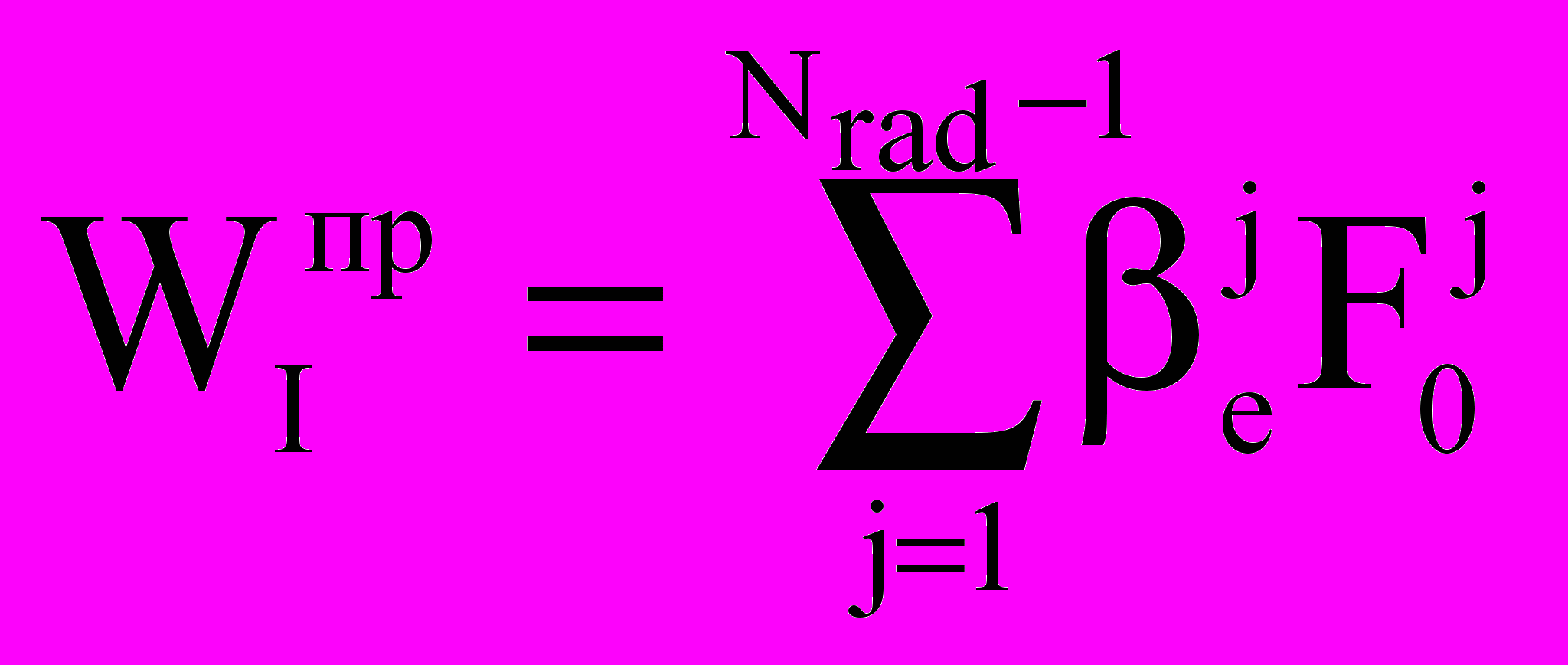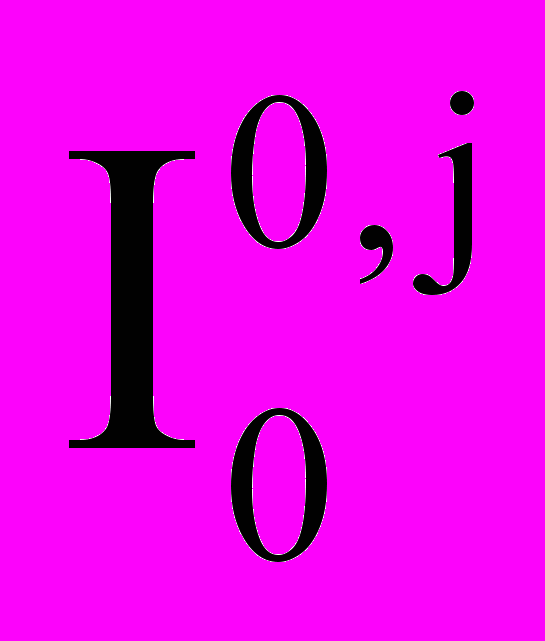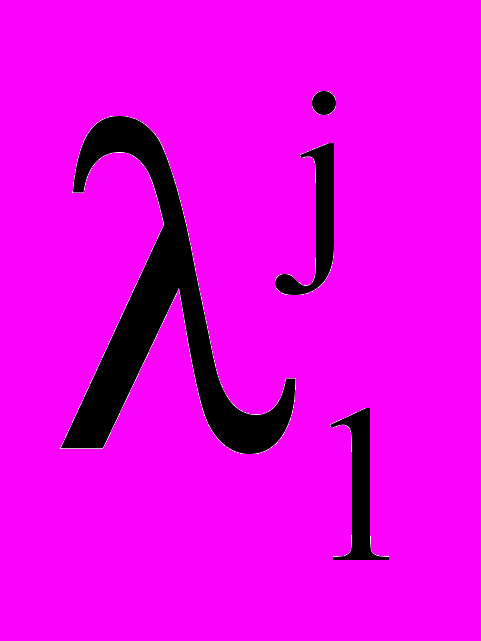где — первый компонент разложения интенсивности излучения в j-м диапазоне (метод сферических гармоник), — интегральная освещенность (прямое солнечное излучение), и 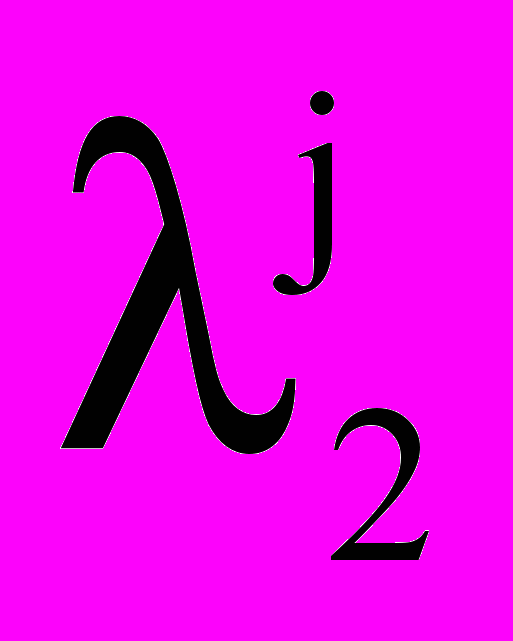— начальная и конечная длины волн, B(T) — функция Планка, , , — коэффициенты ослабления, поглощения и рассеивания. находится обратной трассировкой луча, что упрощает вычисления, особенно в областях сложной формы.

Запишем уравнения для фазы тяжелых пылевых частиц:

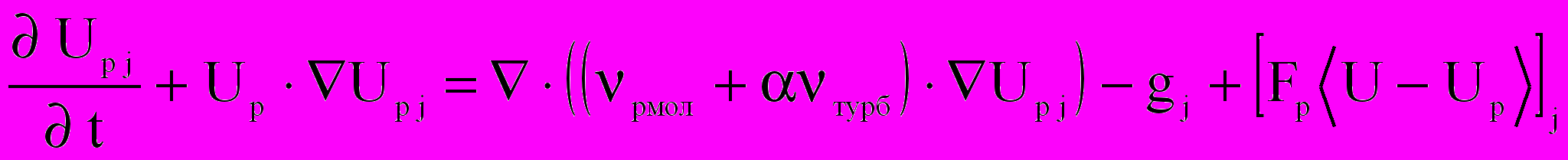; j = 1, 2, 3;

,

где U_p — вектор скорости пылевой фазы, _pмол — кинематическая вязкость пылевой фазы, g₁ = 0, g₂ = 0, g₃ = g, 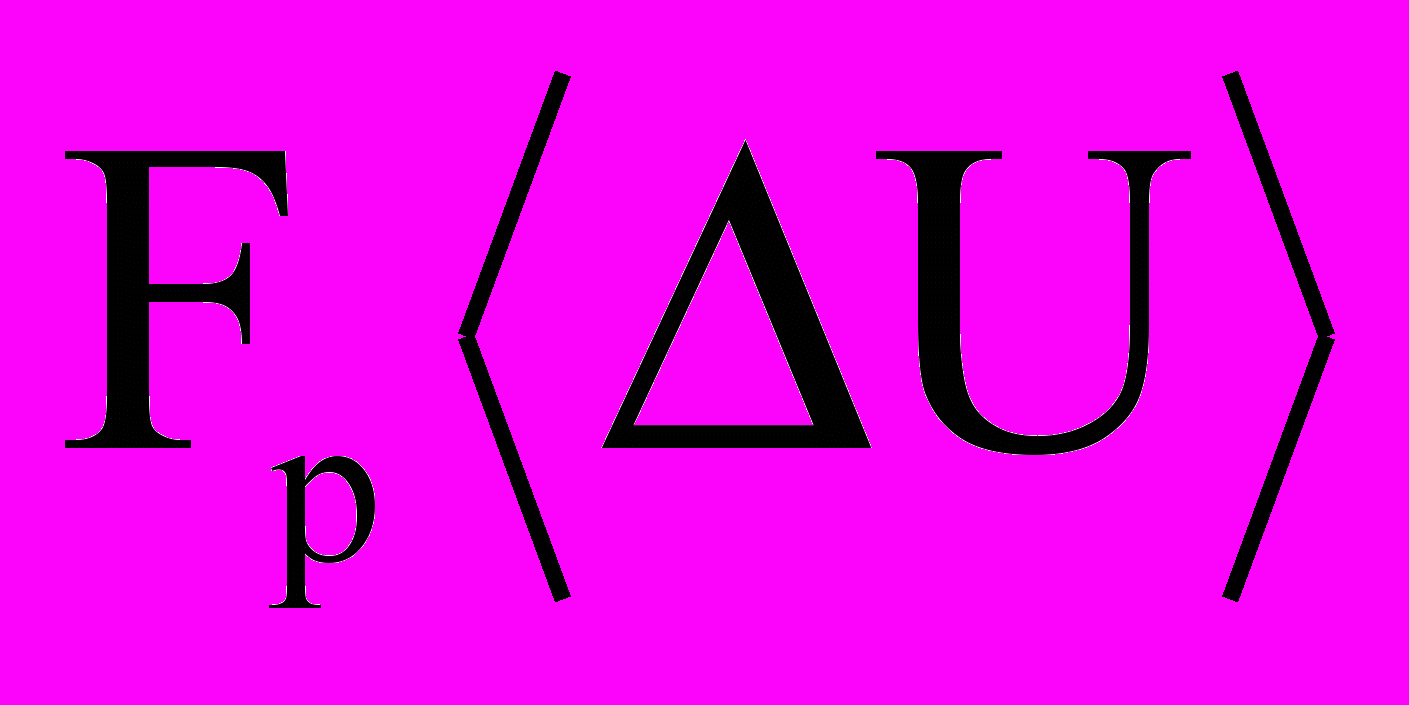— сила сопротивления частицы потоку, _p — плотность пыли, D_ и _ — коэффициенты.

Запишем уравнения для фазы капель из Z компонентов:

;

;

; ; ;

;

; ; ;

; ; ;

; ; ;

;

;

; ; ;



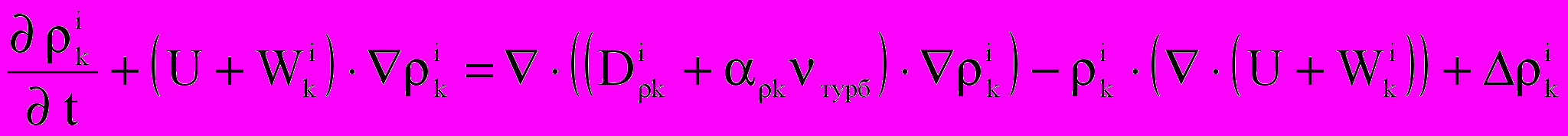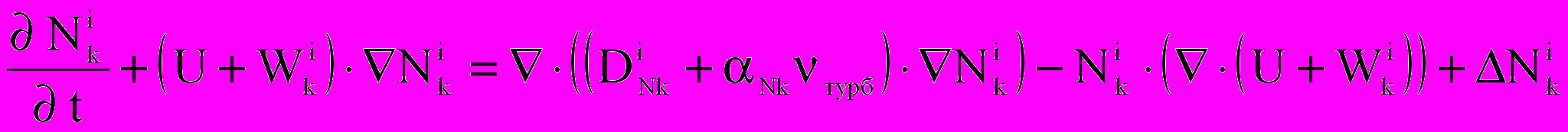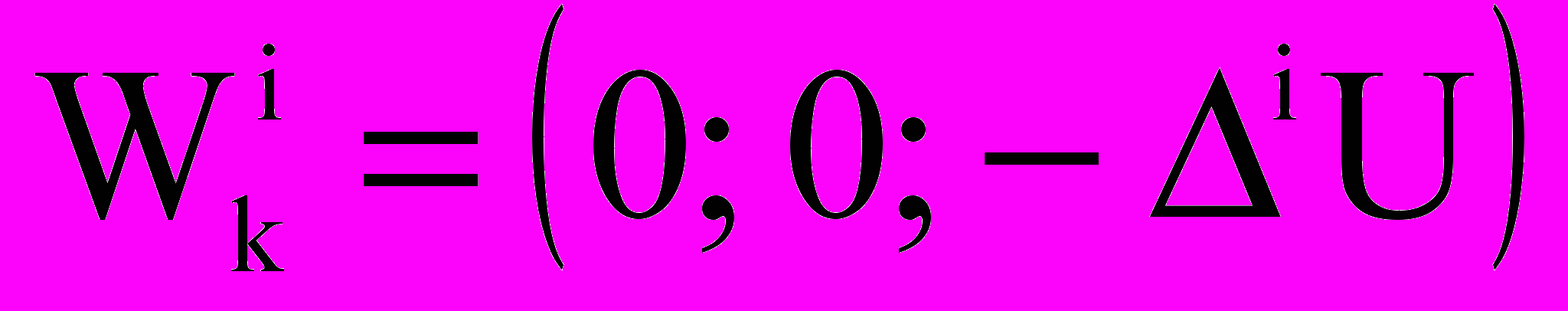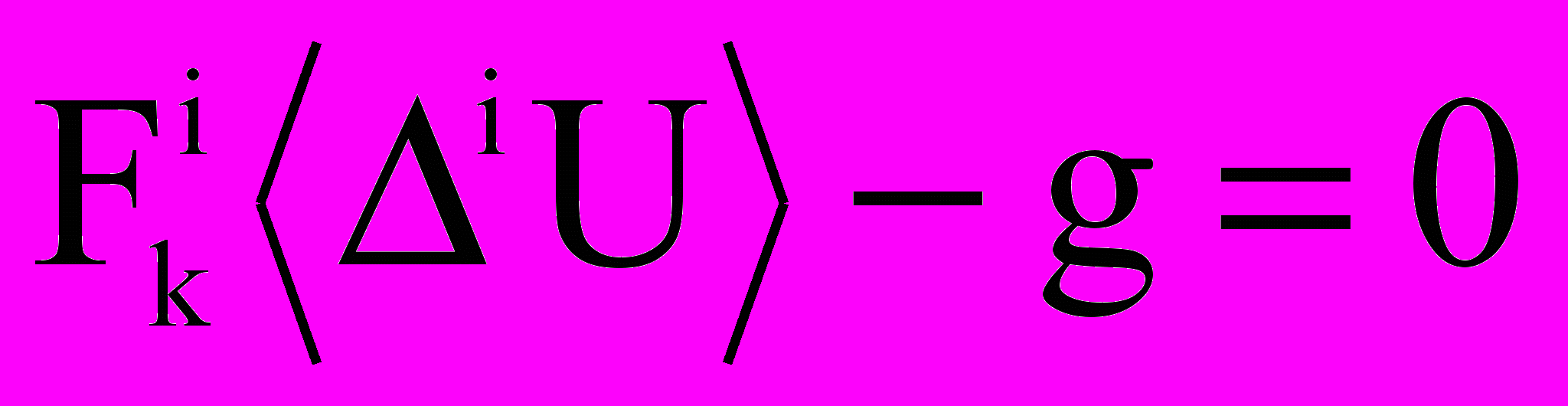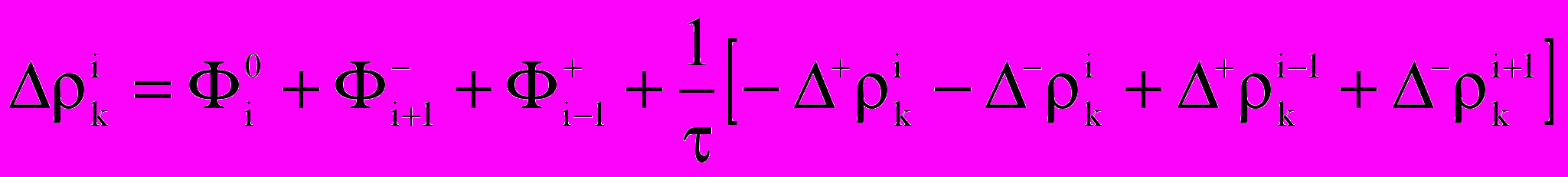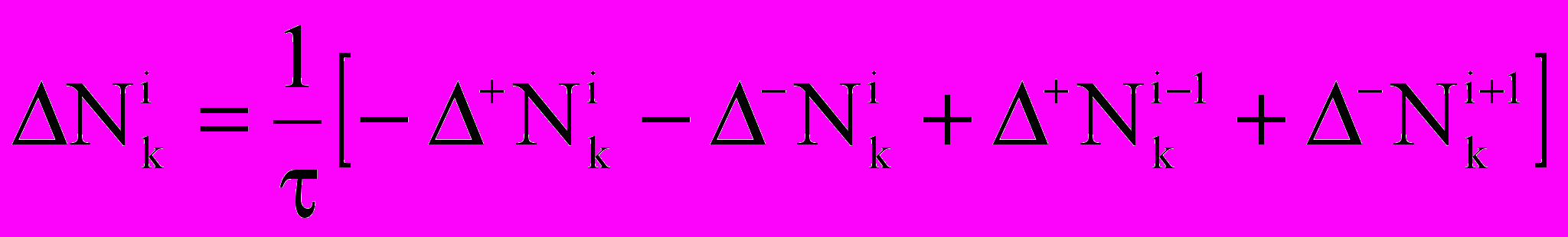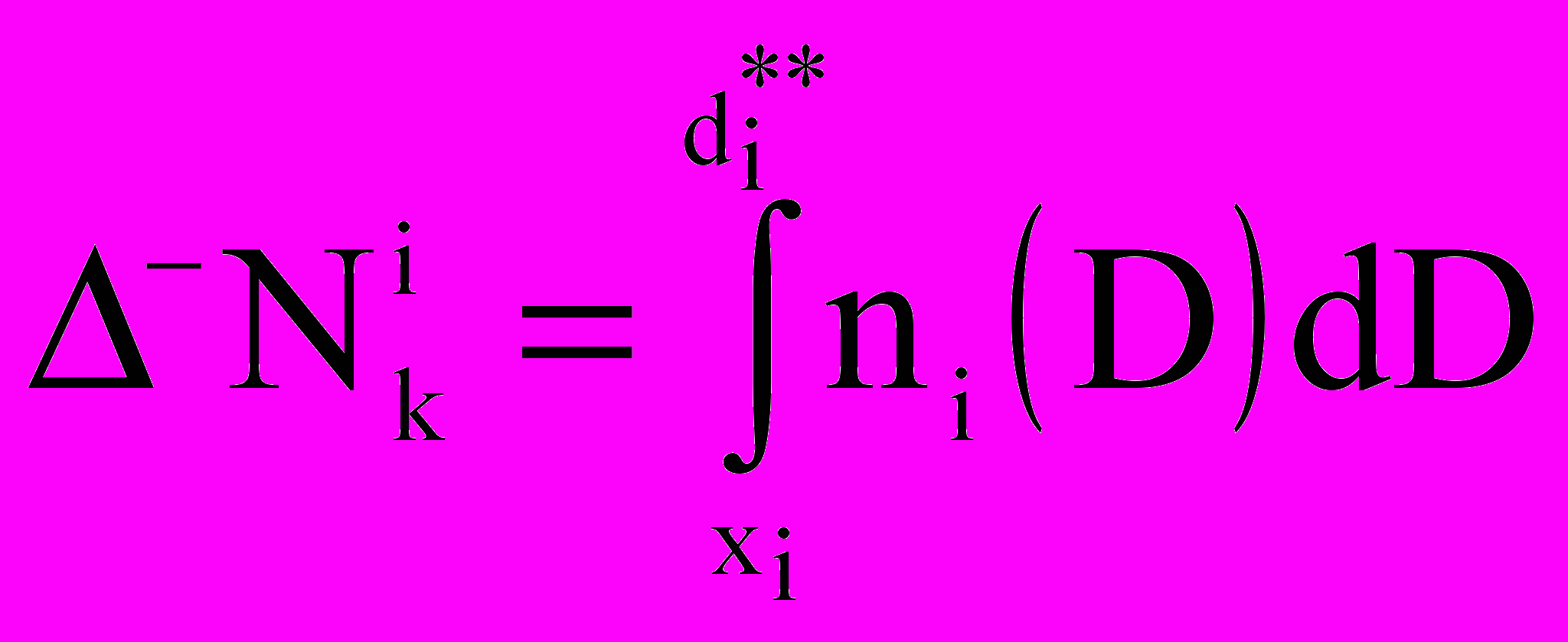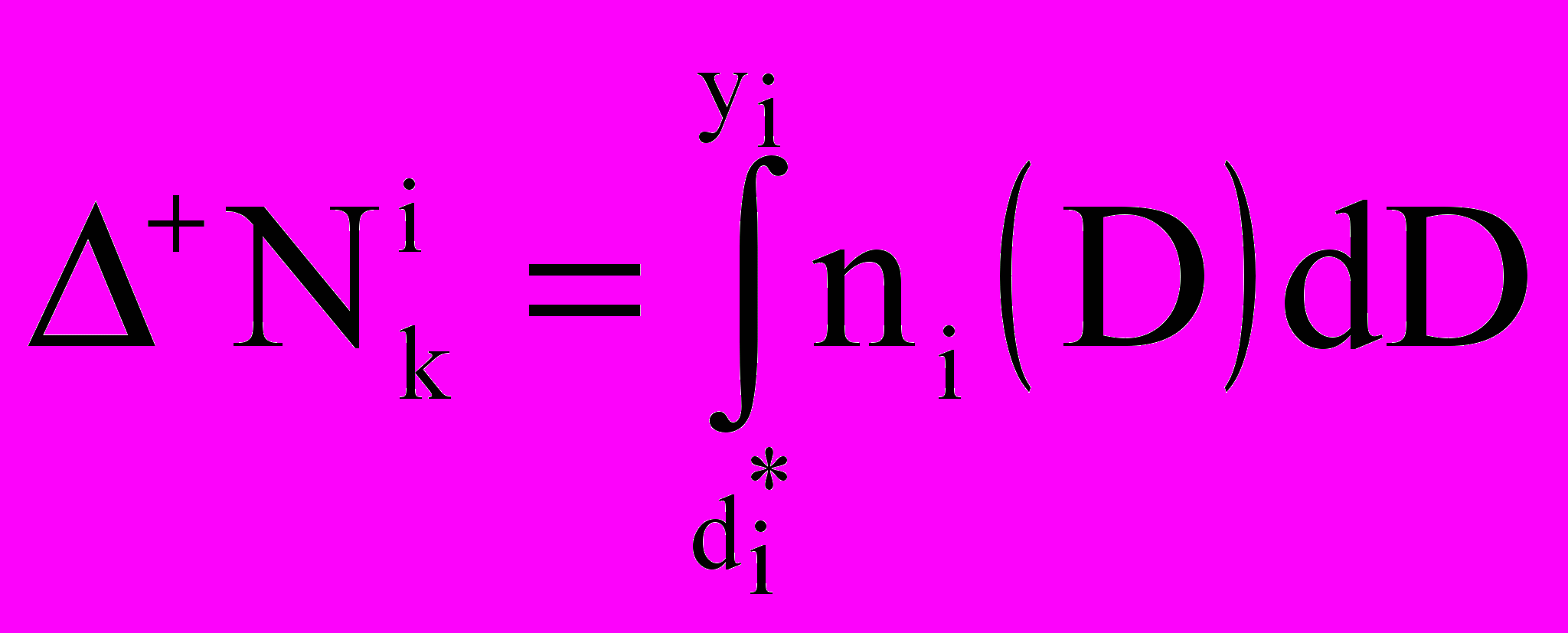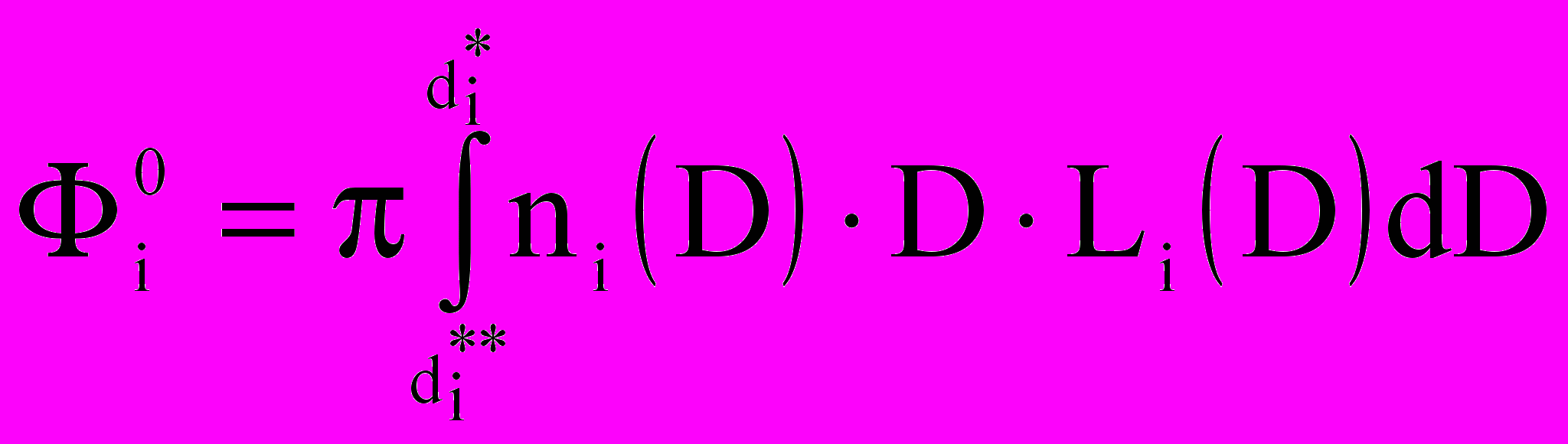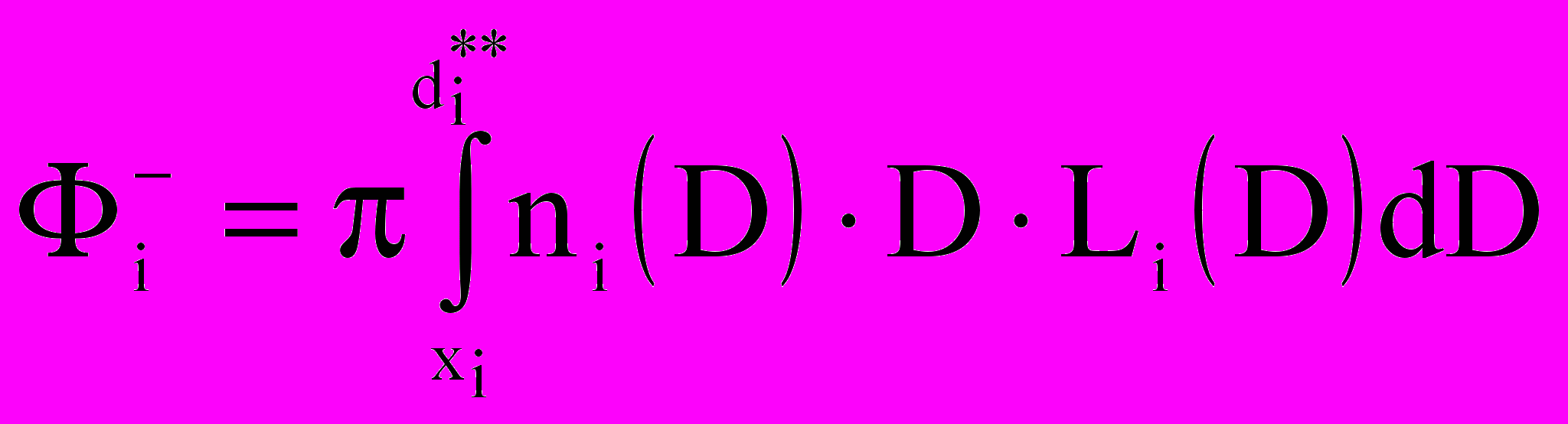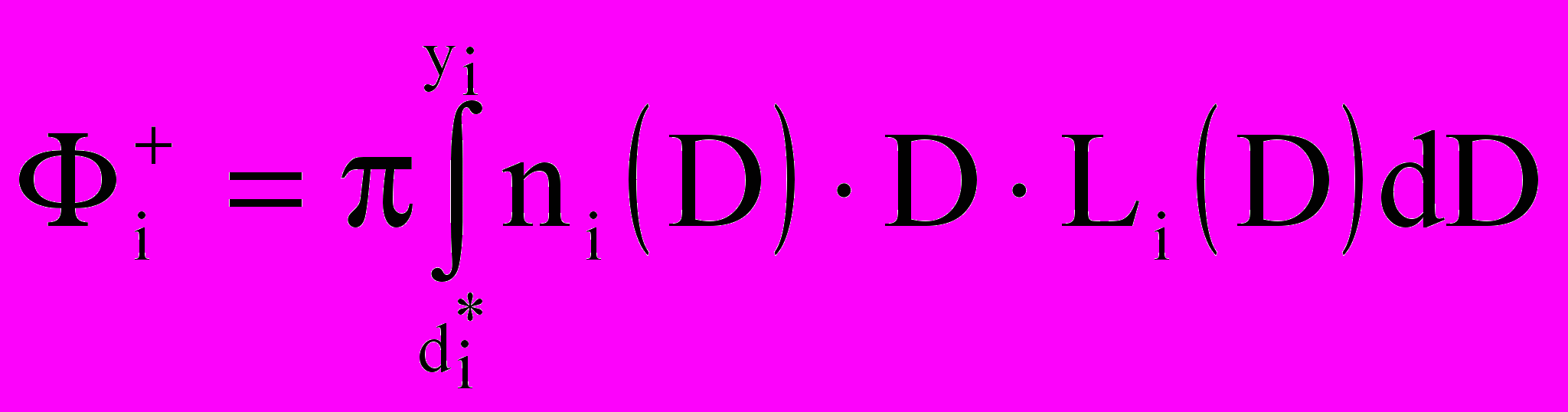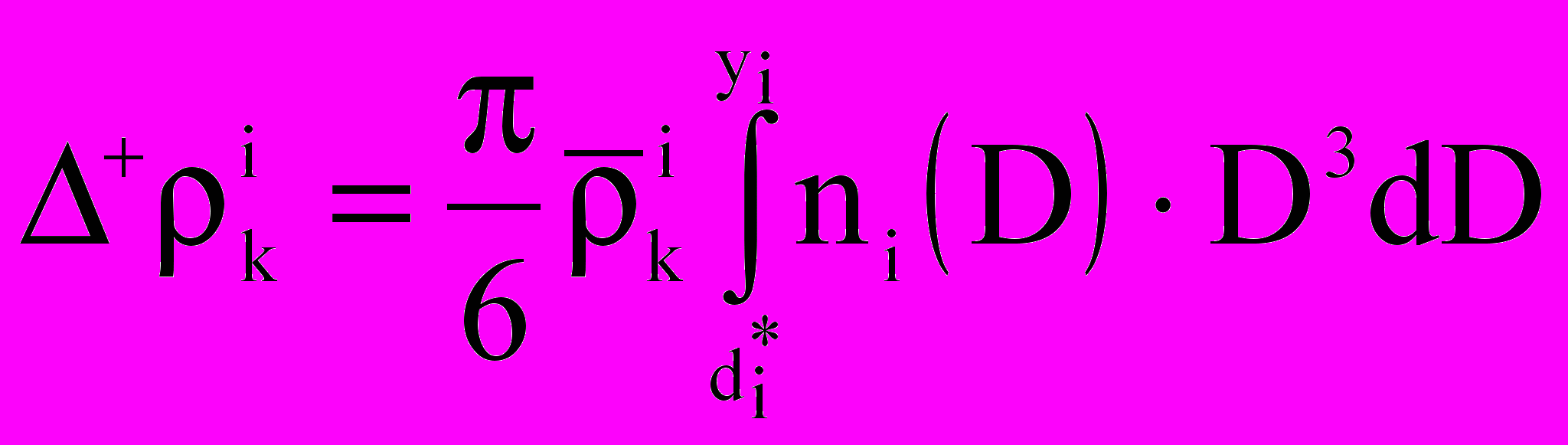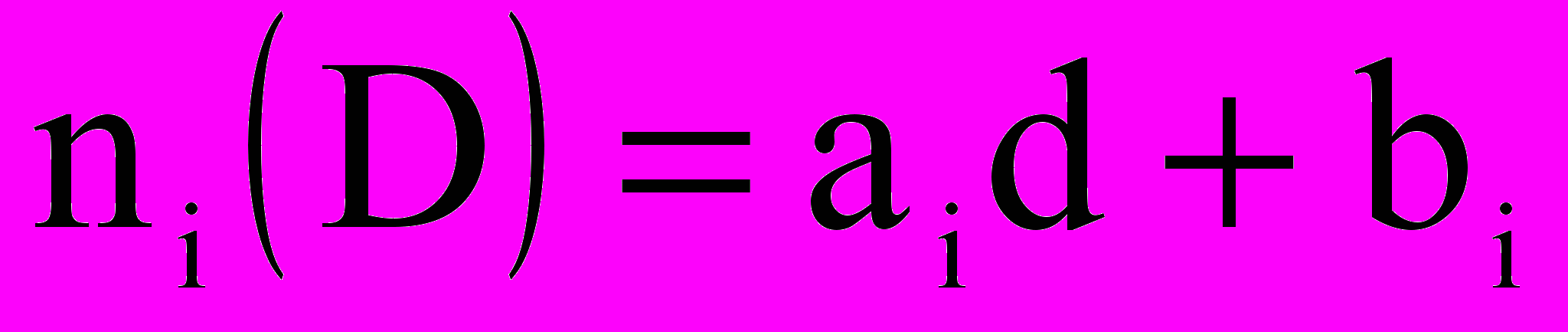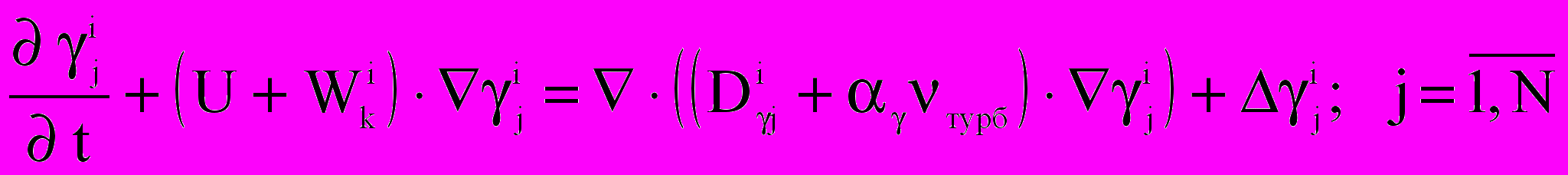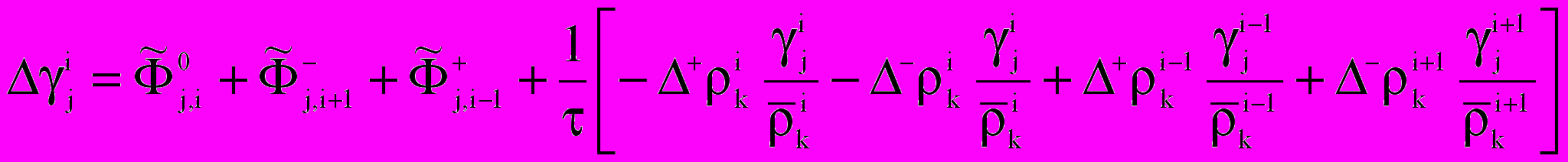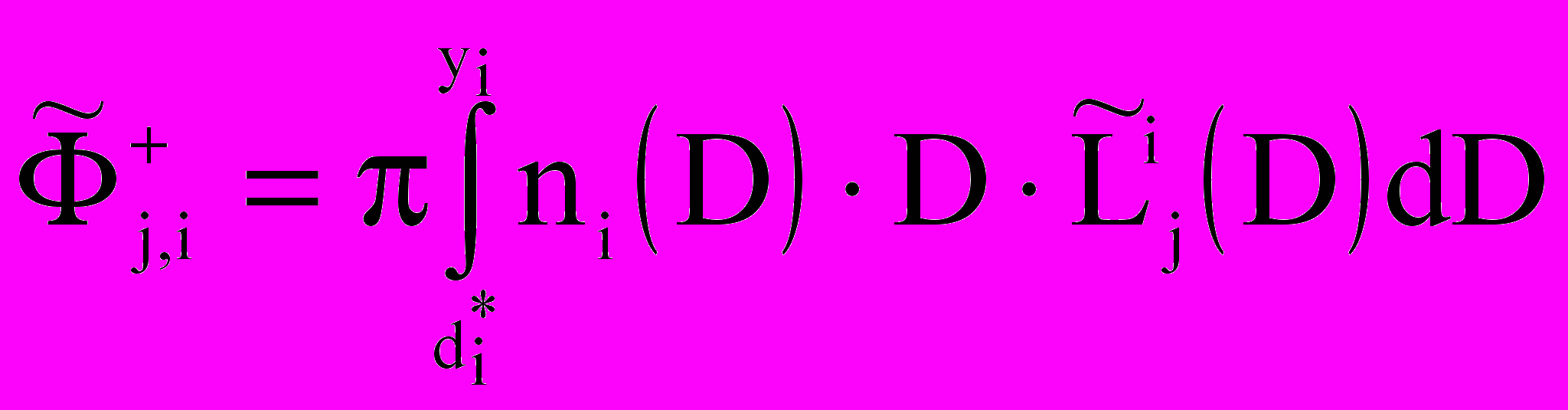где , , 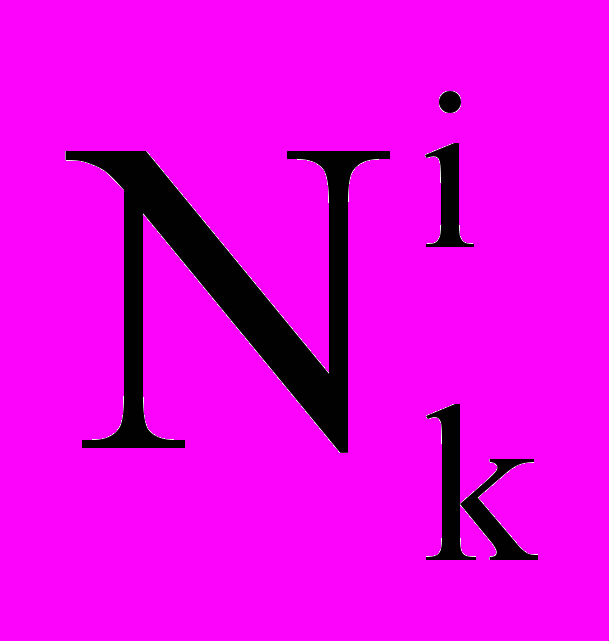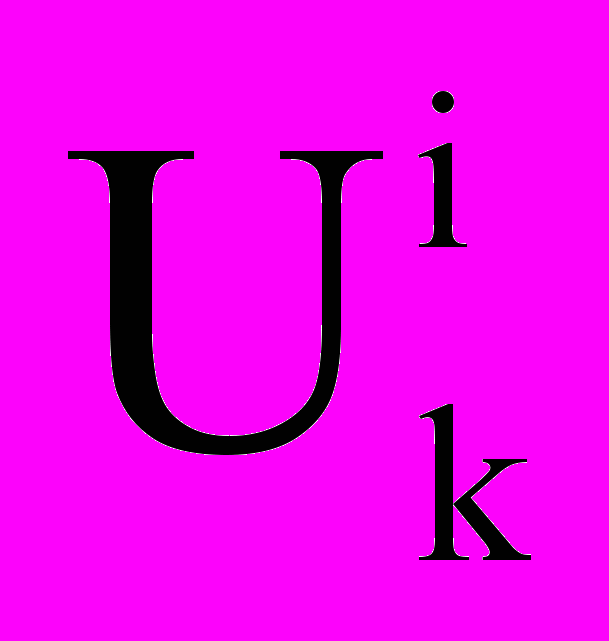— плотность, концентрация и вектор скорости i-го компонента, 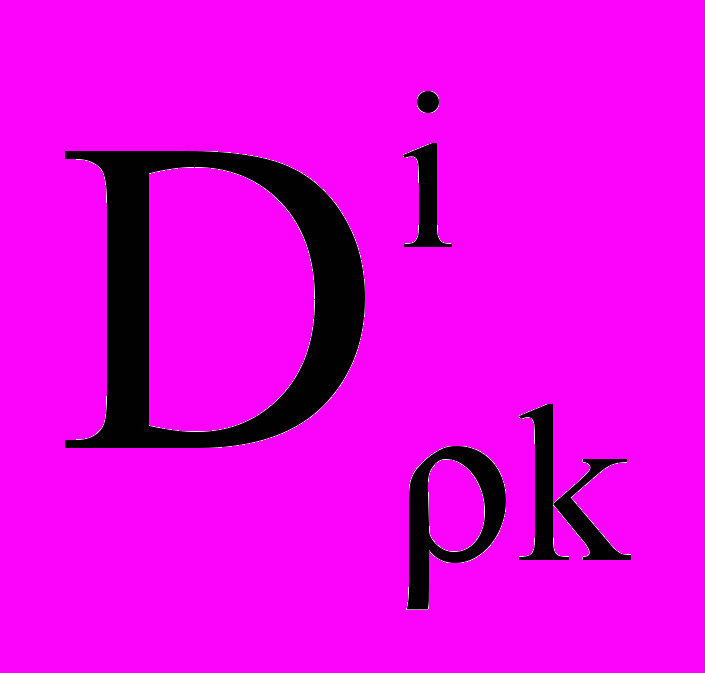, , 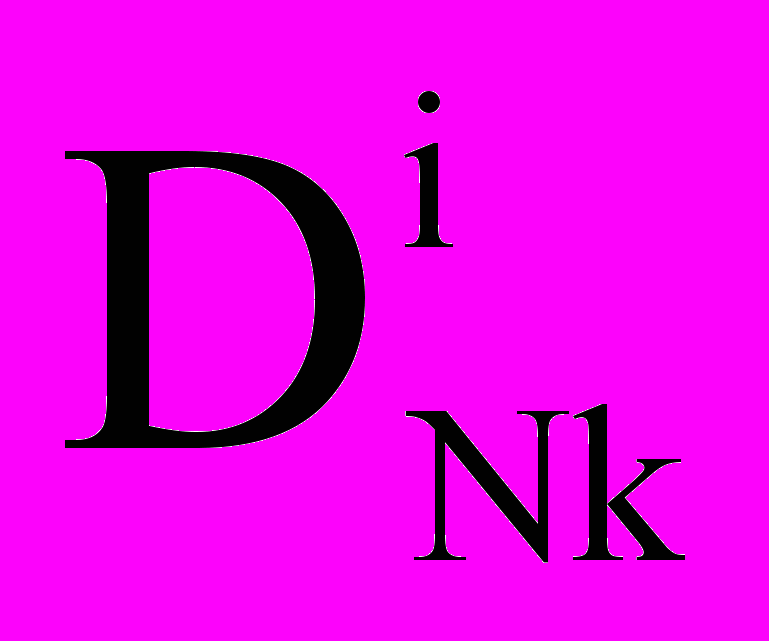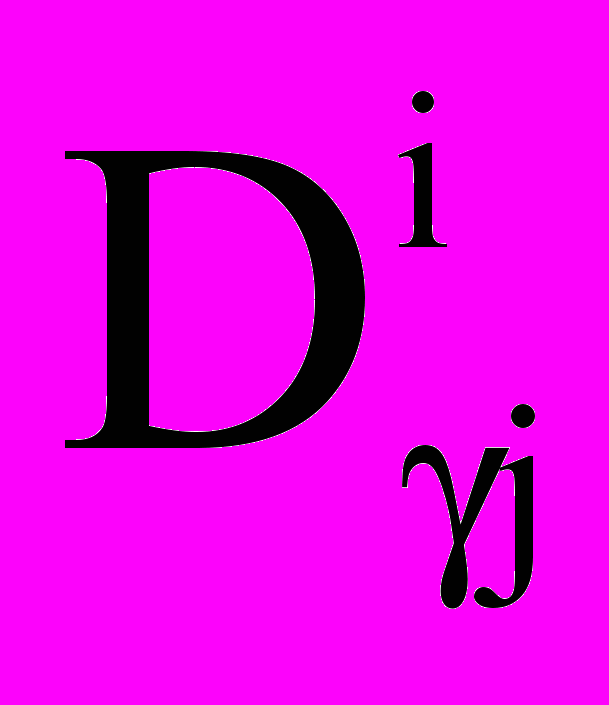и  — коэффициенты, 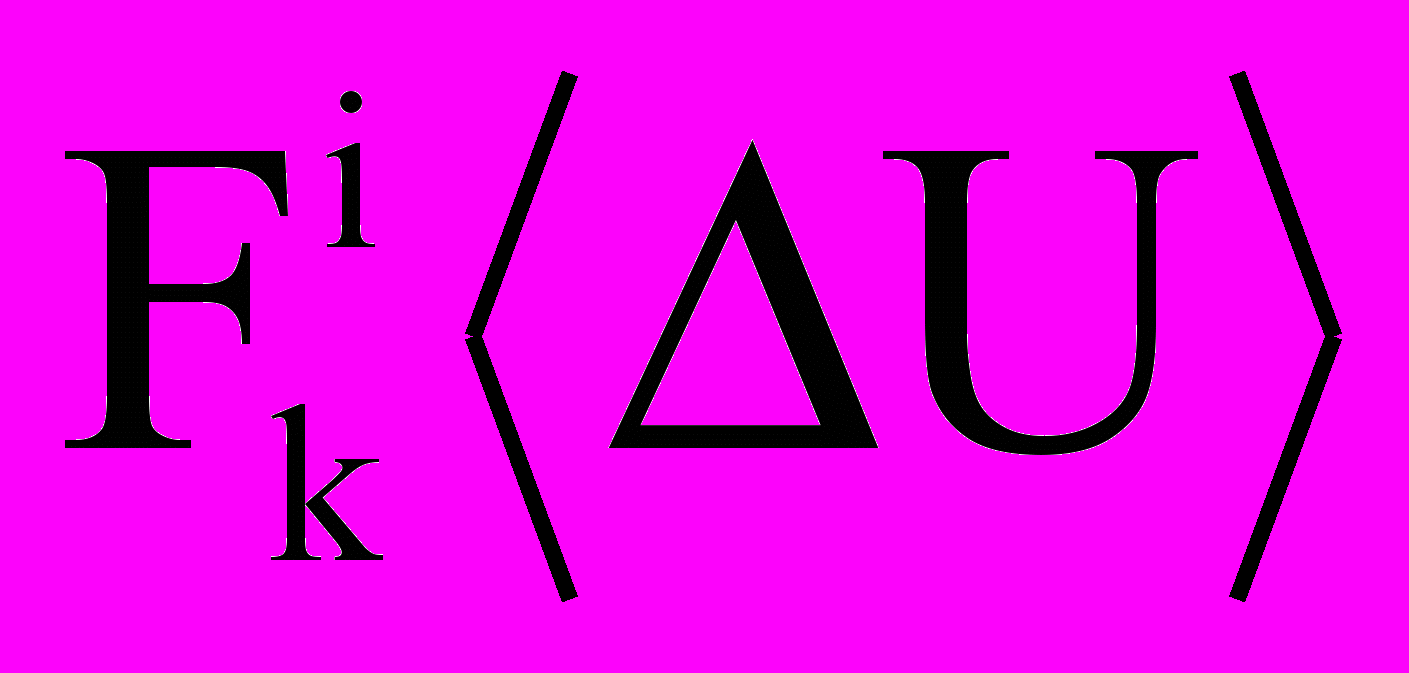— сила сопротивления потоку с учетом деформации,  — шаг интегрирования по времени, L_i(D) и 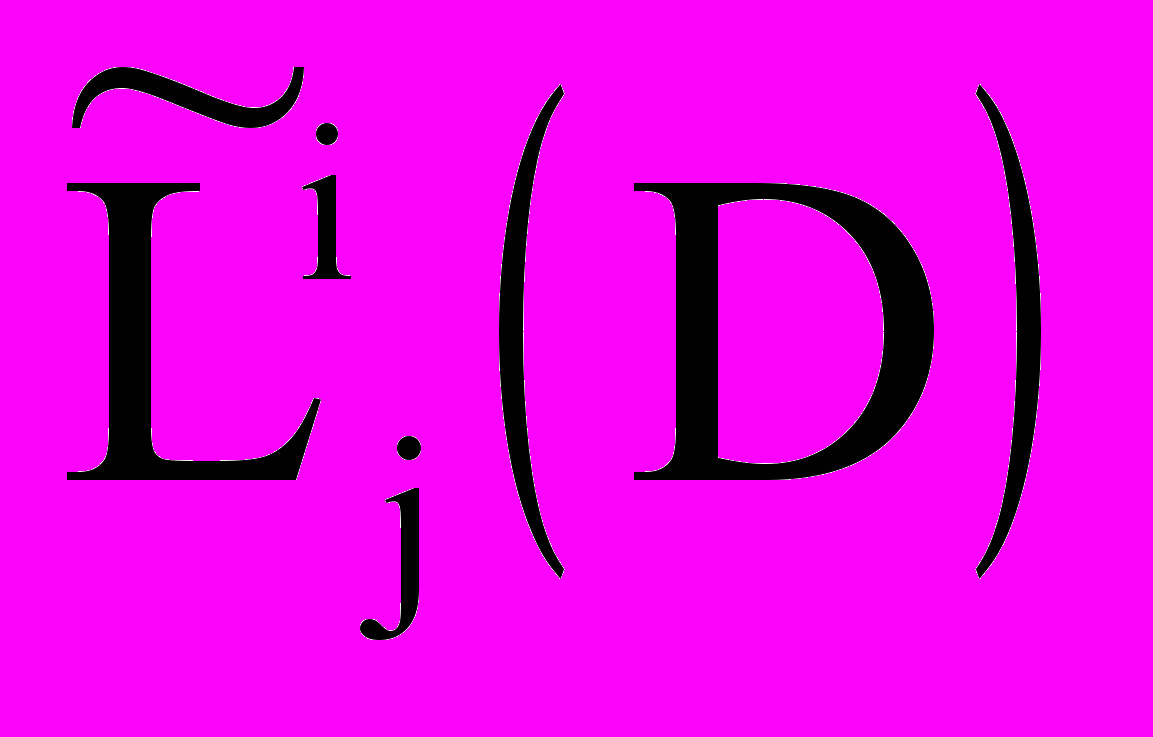— потоки пара и j-го газа между i-м компонентом и средой, 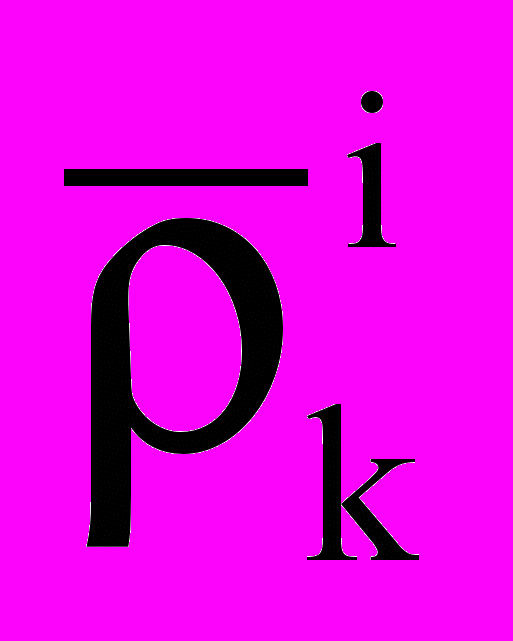— плотность воды, 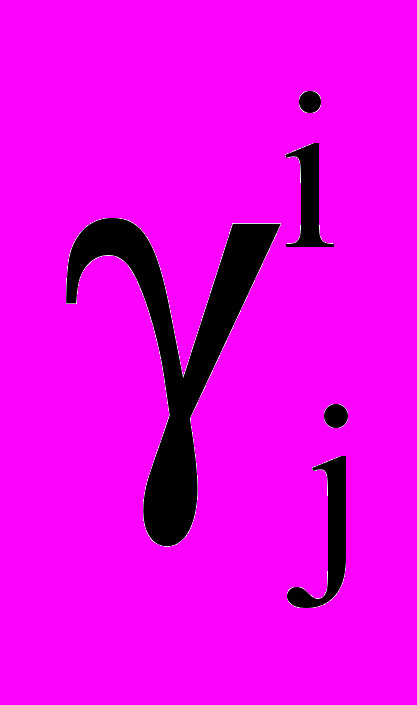— концентрация j-го газа в каплях i-го компонента, 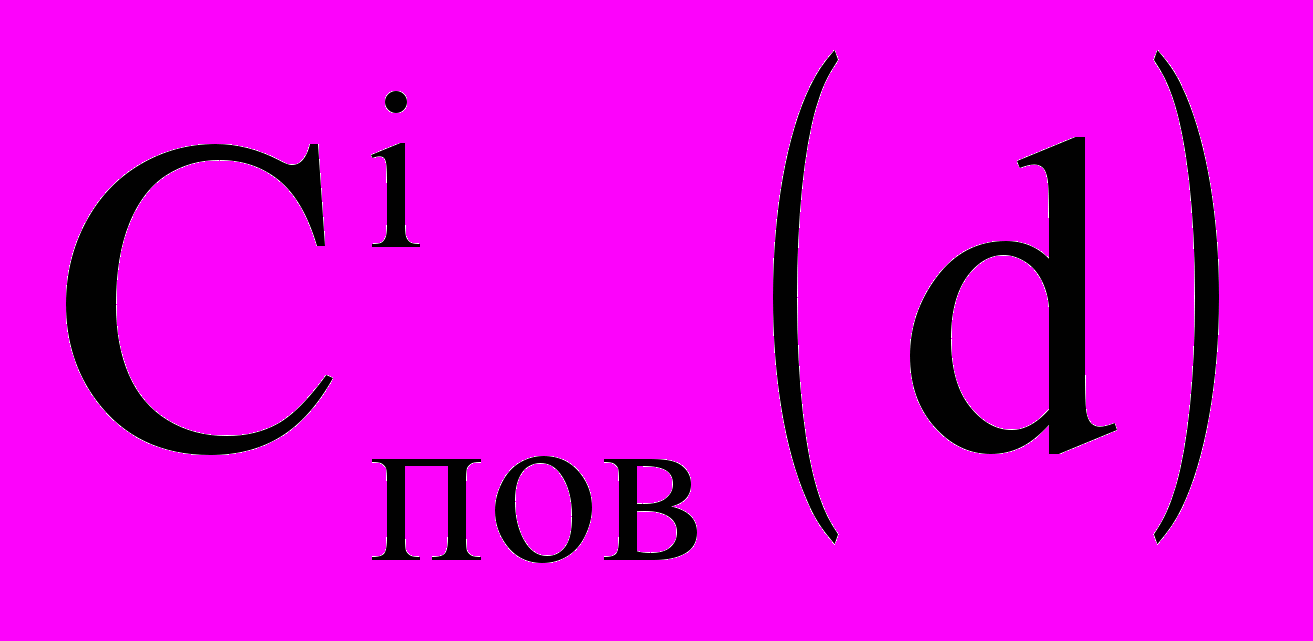— концентрация пара на поверхности капли (с поправками Кельвина и Кехлера). Предложен алгоритм расчета параметров a_i и b_i кусочных распределений (линейных при полном заполнении [капли с диаметрами от d_i до d_i+1] и равномерных при частичном заполнении [с поиском начала x_i или конца y_i заполнения]) путем интерполяции по значениям и 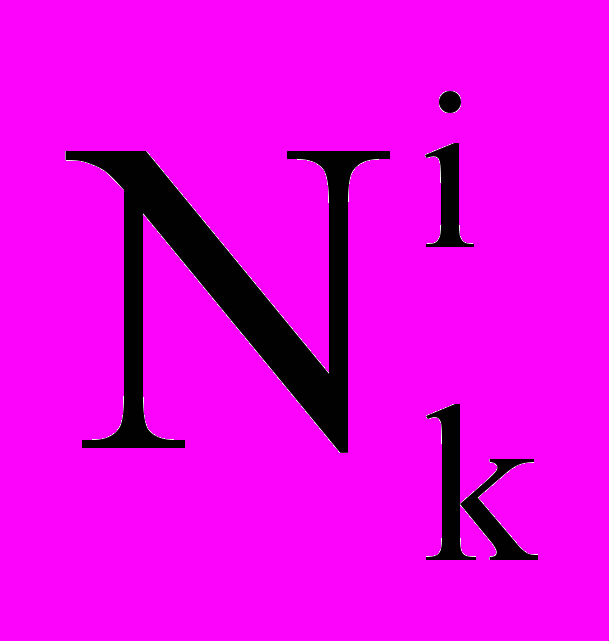. Алгоритм имеет низкие трудозатраты и работает даже с разрывными распределениями. Модель апробирована в численных экспериментах на многопроцессорных системах МВС-1000, в том числе на реальных данных.

Работа выполнена при финансовой поддержке Минобразования и науки (грант РНП.2.2.1.1.7280).