Всероссийская олимпиада школьников «Шаг в будущее» Математика

Вид материала

Документы

Подобный материал:

• Всероссийская филологическая олимпиада «Шаг в будущее» для школьников по русскому языку, 126.58kb.
• Конкурс интеллектуалов «Технология развития памяти и логики» Всероссийская олимпиада, 95.9kb.
• Всероссийская Интернет-олимпиада школьников, студентов, аспирантов и молодых ученых, 11.94kb.
• Секретариат программы «Шаг в будущее» Почтовый адрес, 1818.72kb.
• Пояснительная записка в 1964 году Министр просвещения, 2541.4kb.
• Программа для молодёжи и школьников «шаг в будущее», 263.02kb.
• Российской научно-социальной программы для молодежи и школьников «Шаг в будущее» общие, 219.31kb.
• Международные олимпиады по общеобразовательным предметам и всероссийская олимпиада, 202.54kb.
• Творческая работа Окристаллах, 182.71kb.
• Проектная работа Чудо люминесценции, 436.64kb.

Всероссийская олимпиада школьников «Шаг в будущее»

Математика

Направление: Математика в современном мире


Задания олимпиады по математике

1. Три различных числа образуют геометрическую прогрессию, а их попарные суммы, взятые в некотором порядке – арифметическую прогрессию. Найдите знаменатель геометрической прогрессии.


2. Длины боковых сторон трапеции равны 3 и 5. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит её на две части, отношение площадей которых равно 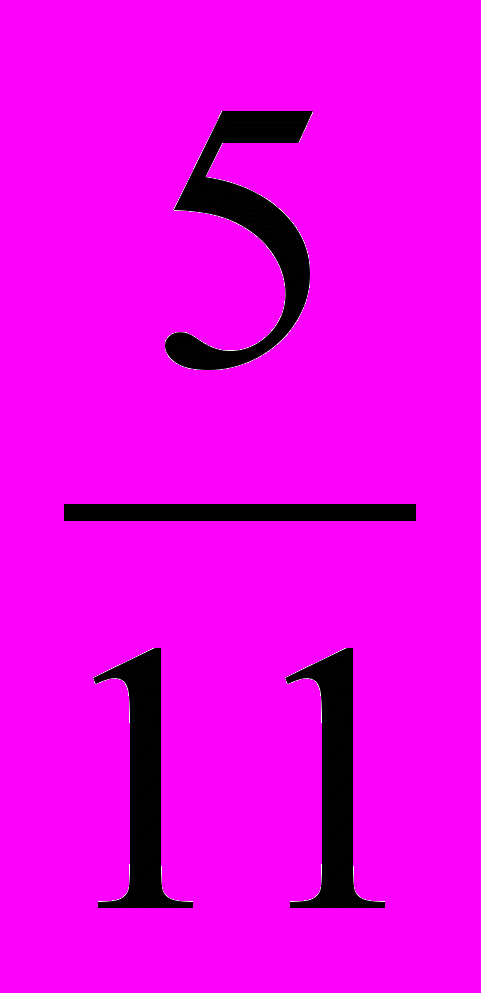. Найти длины оснований трапеции.

3.Решите уравнение




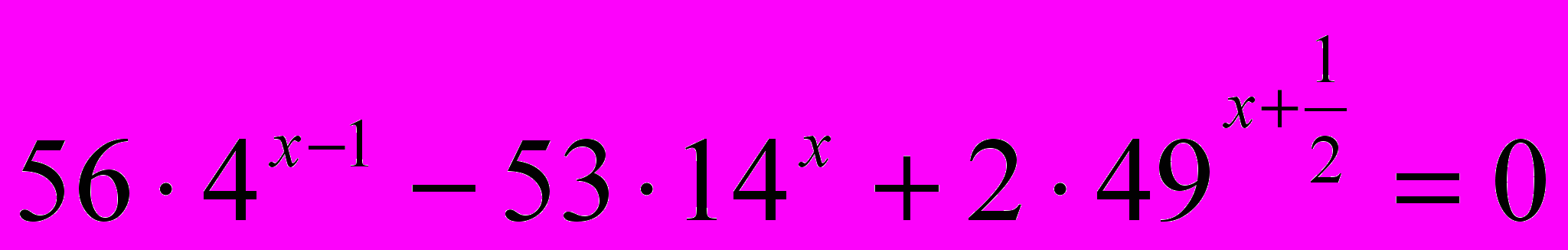
4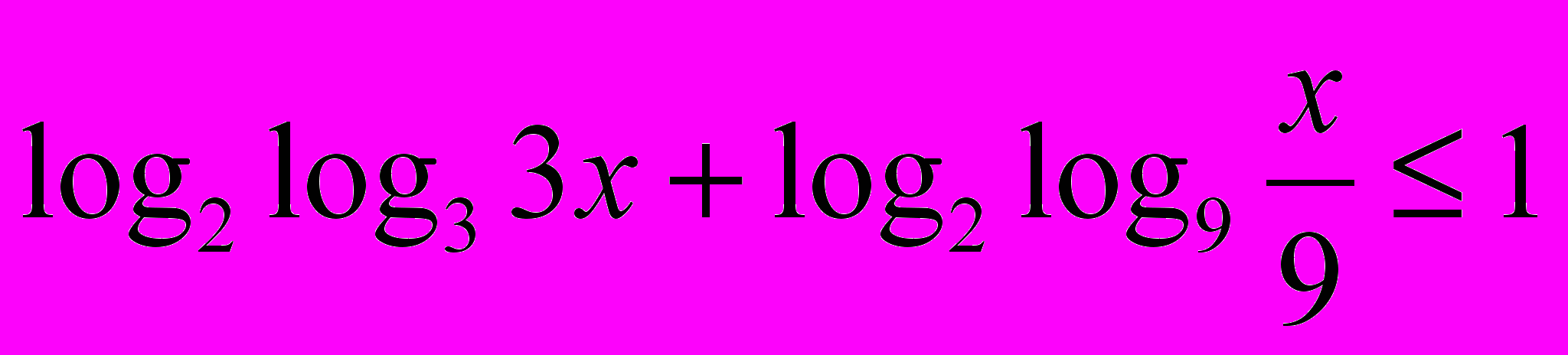. Решите неравенство


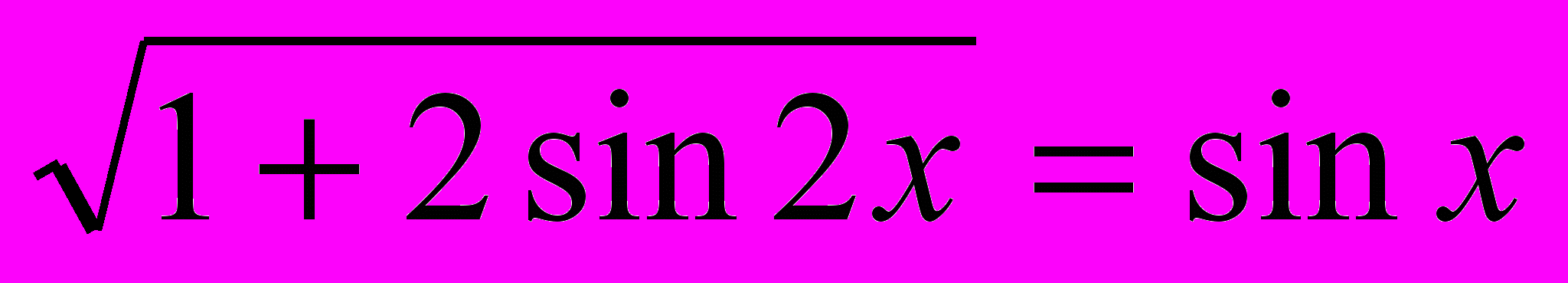
5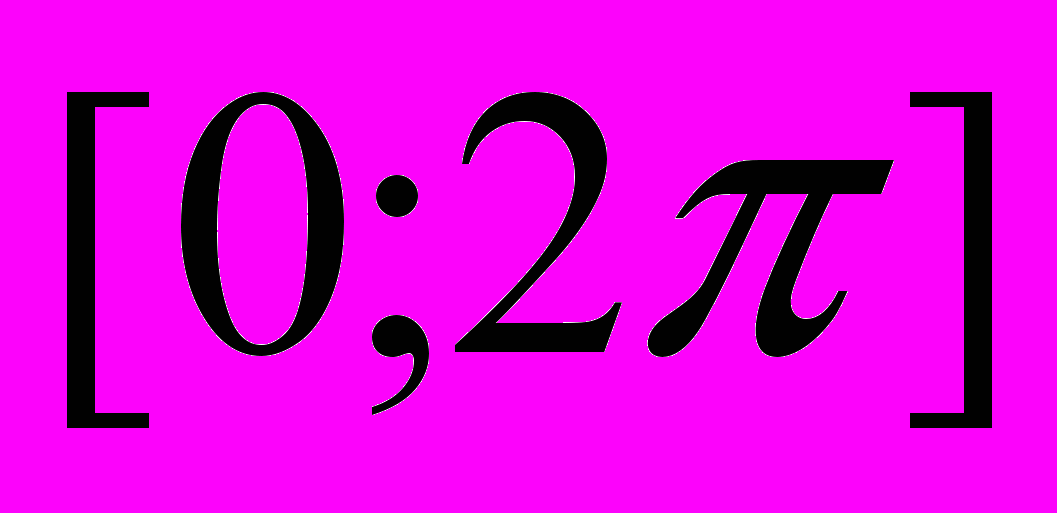. Найдите все решения уравнения на отрезке

6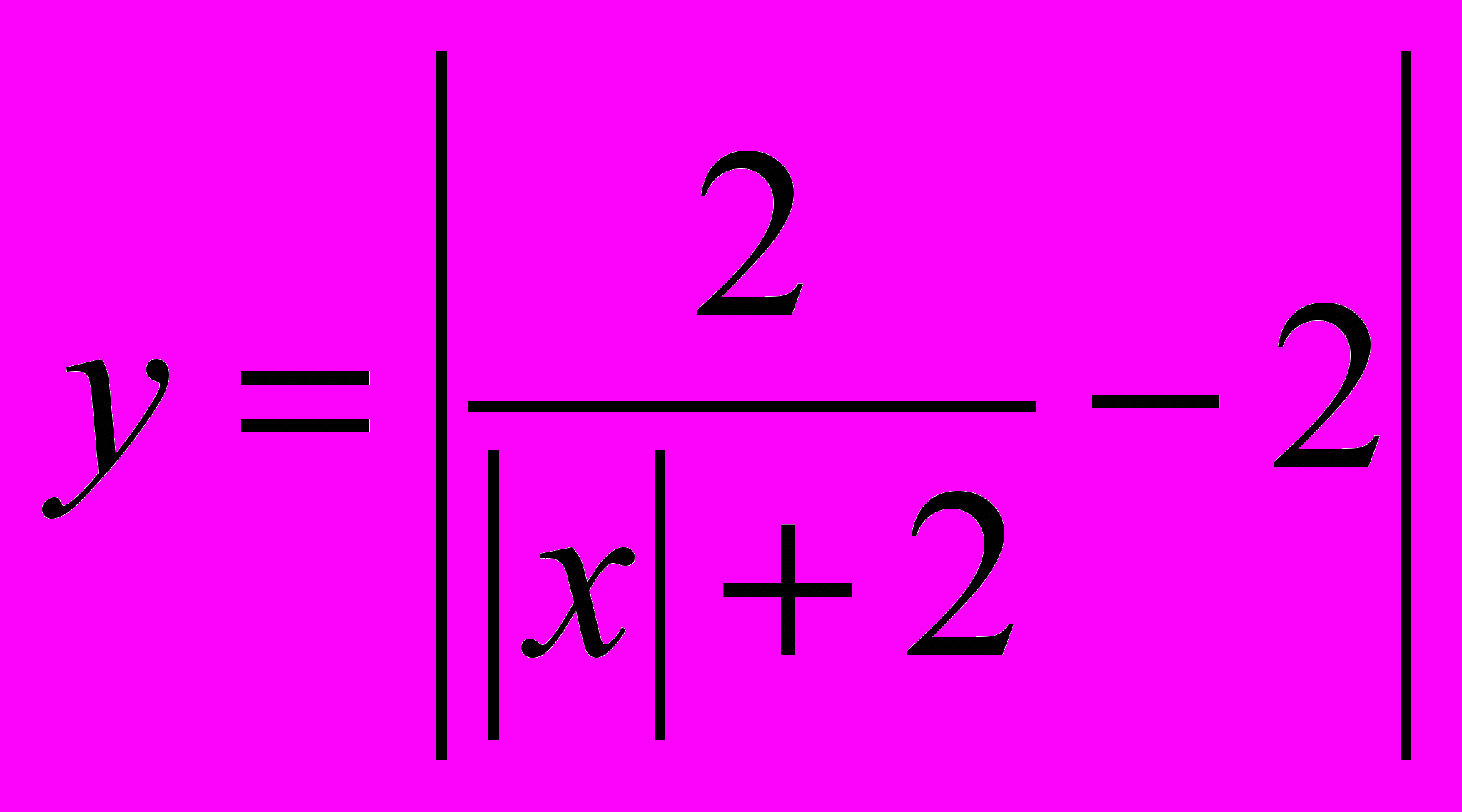. Найдите множество значений функции

7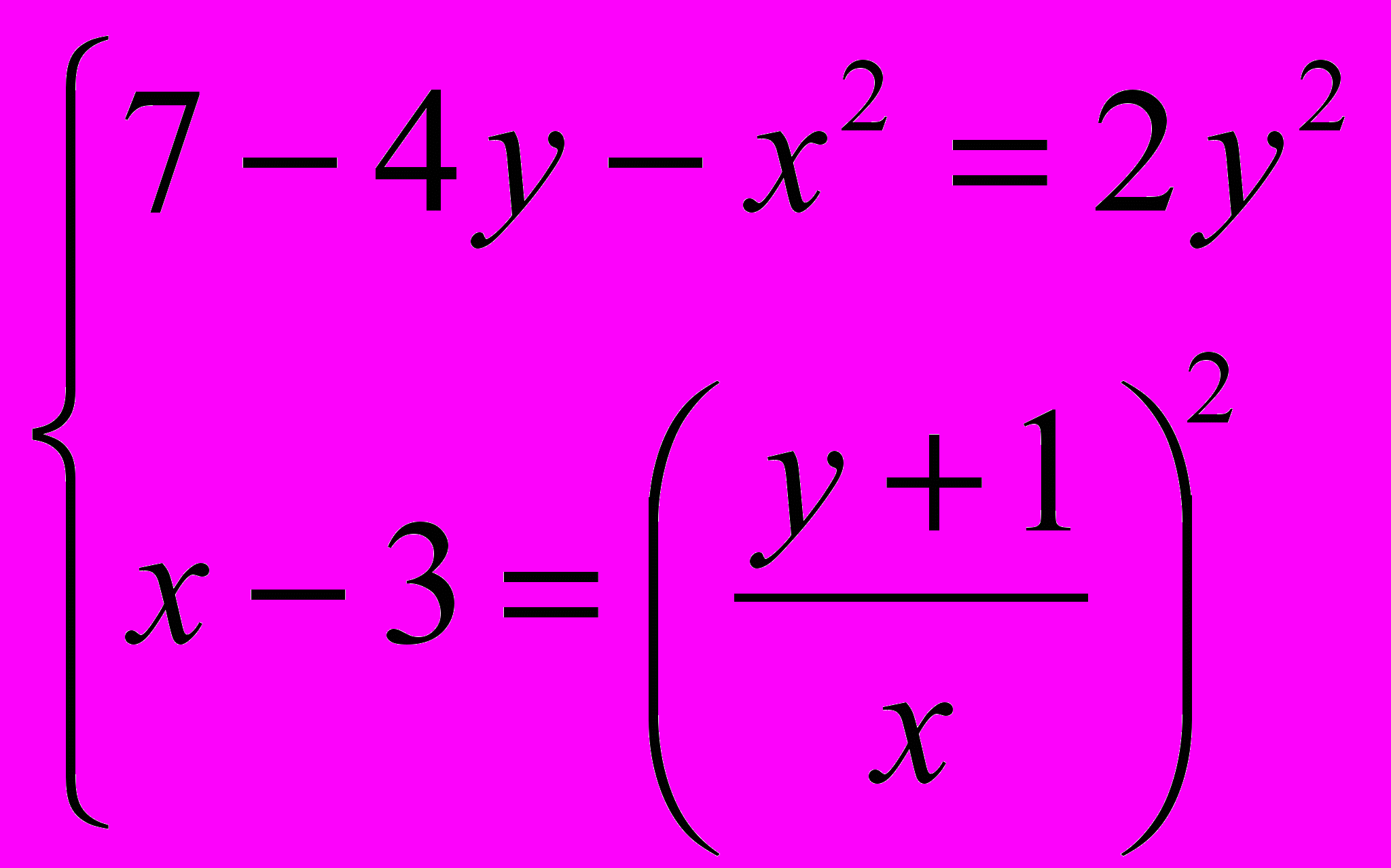. Решите систему


8. Дана прямая призма ABCA'B'C', стороны основания которой AB=BC=1, AC= .
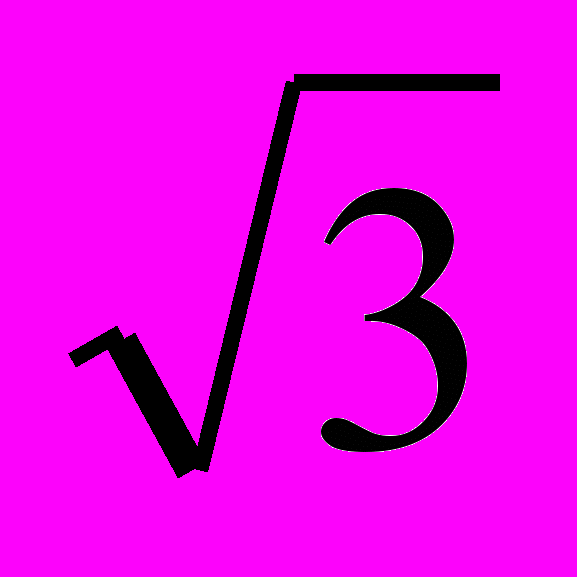В каком отношении объём вписанного в призму цилиндра делится плоскостью ACB' ?

9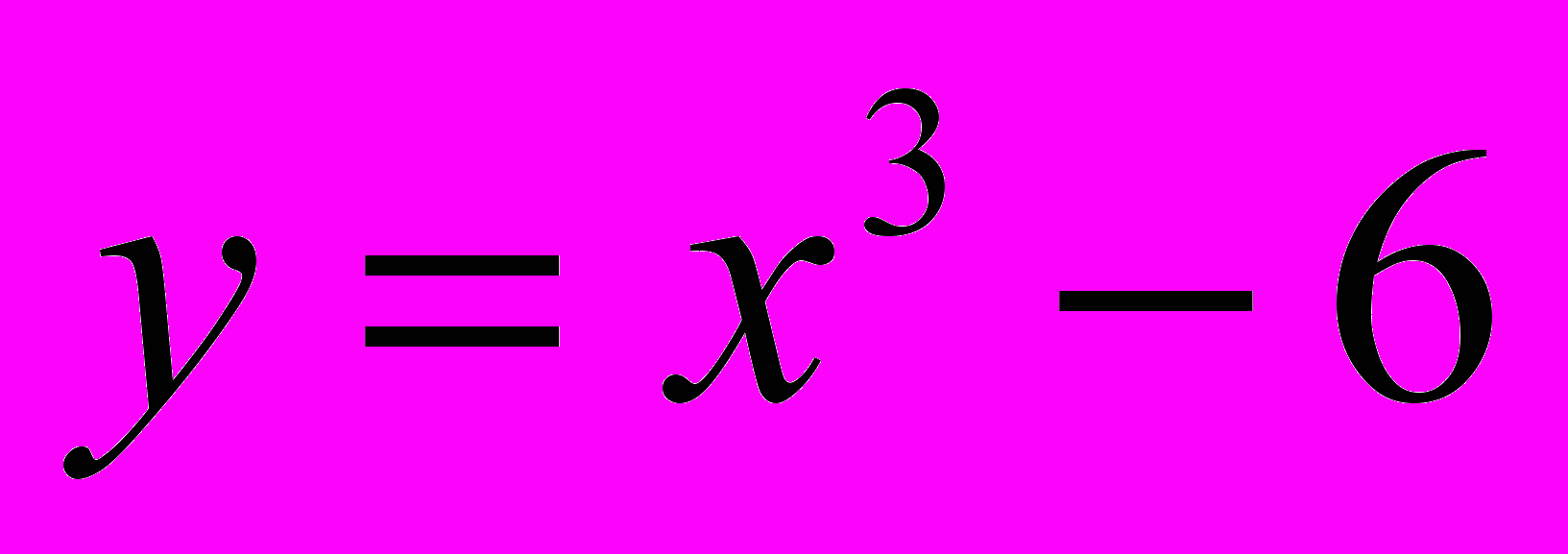. Две параллельные касательные к графику функции пересекают оси координат: первая в т. А и В, вторая в т. C и D. Точка О - начало координат. Найдите площадь треугольника АОВ, если известно, что она в 4 раза меньше, чем площадь треугольника COD.

10. В равнобедренном треугольнике с боковыми сторонами, равными 1, и основанием, равным а, среди всех вписанных прямоугольников с двумя вершинами на основании треугольника выбран прямоугольник наибольшей площади. При каком значении а площадь этого наибольшего прямоугольника будет наибольшей?

11. При каких значениях параметра a существует такое k, что уравнение

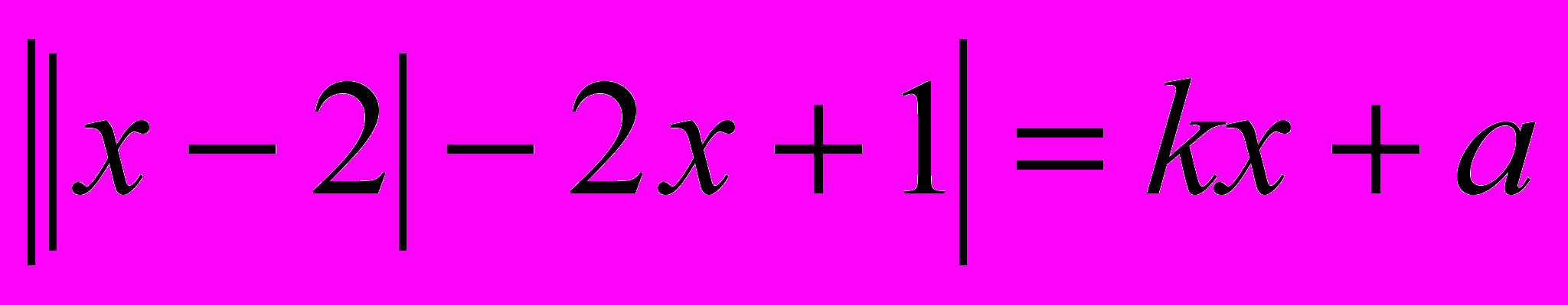имеет ровно три решения?