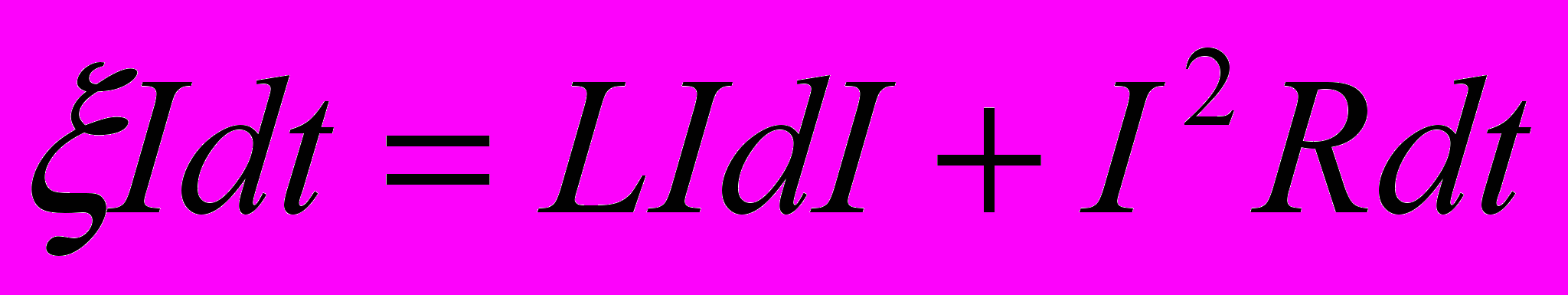Закон полного тока
| Вид материала | Закон |
- Задачи, 847.5kb.
- Магнитное поле в вакууме, 56.29kb.
- План занятий студентов 2 курса 3 семестр 1 лекционный курс, 72.01kb.
- Разработка урока по физике по теме Электрическая лампа накаливания и электронагревательные, 105.5kb.
- Урок физика-математика «Расчет комплексных сопротивлений в электрических цепях переменного, 117.95kb.
- Преобразователь измерительный активной мощности трехфазного тока эп8508, 237.92kb.
- Распределительные устройства и подстанции глава 1 распределительные устройства напряжением, 1894.23kb.
- Распределительные устройства и подстанции глава 1 распределительные устройства напряжением, 1787.75kb.
- Тема «Электрический ток в металлах. Действия электрического тока.», 113.8kb.
- Терминология Глухозаземленная нейтраль, 249.33kb.
Лекция 10
ЗАКОН ПОЛНОГО ТОКА
Напряженность МП. Закон полного тока в магнетиках. Условия для компонент напряженности и индукции МП на границе раздела магнетиков. Энергия и плотность энергии МП в магнетиках.
- Магнитное поле в веществе является суперпозицией двух полей – внешнего, создаваемого макротоками, и внутреннего, создаваемого микротоками.

-
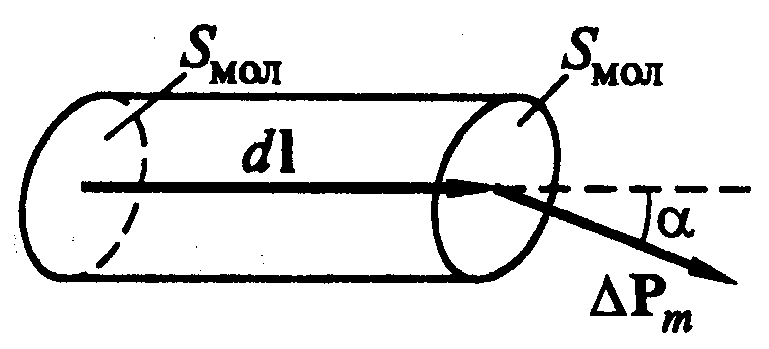
Наведенному магнитному моменту Pm атома (молекулы) можно сопоставить замкнутый молекулярный ток Iмол с площадью витка Sмол
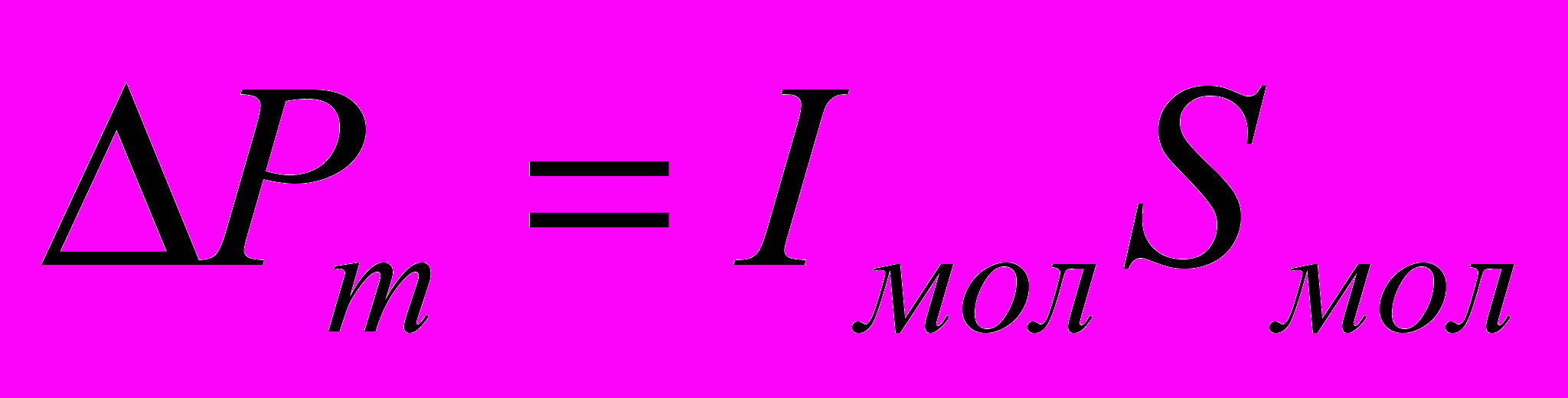
- Вклад дают только те токи, которые нанизаны на замкнутый контур L. Элементу dl этого контура соответствует ток
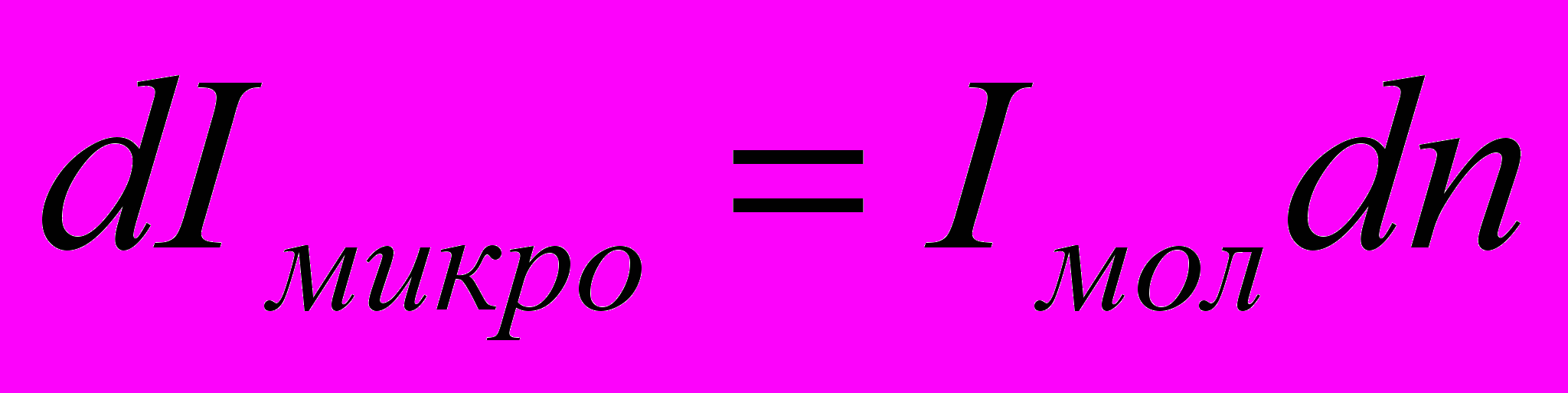
где dn – число атомов вещества внутри косого цилиндра с площадью основания Sмол (
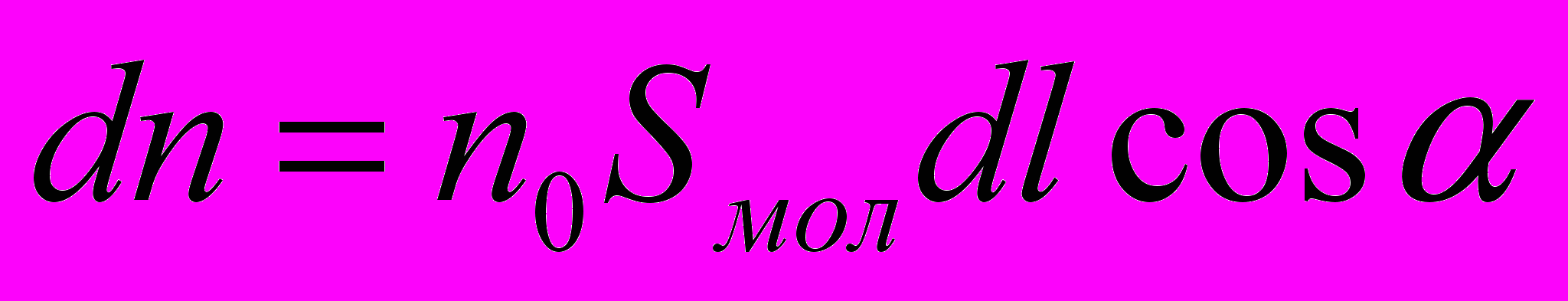 , n0 – концентрация атомов)
, n0 – концентрация атомов)- Полная величина тока определится
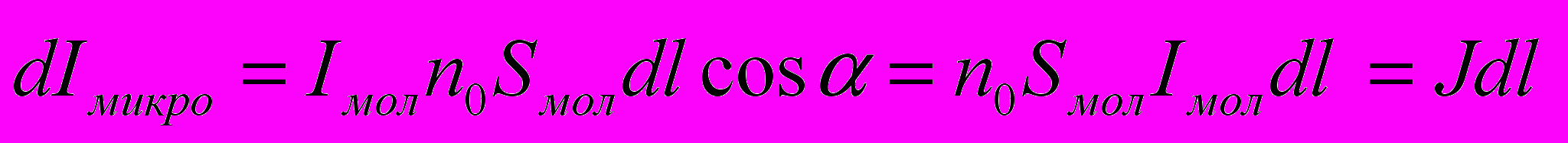
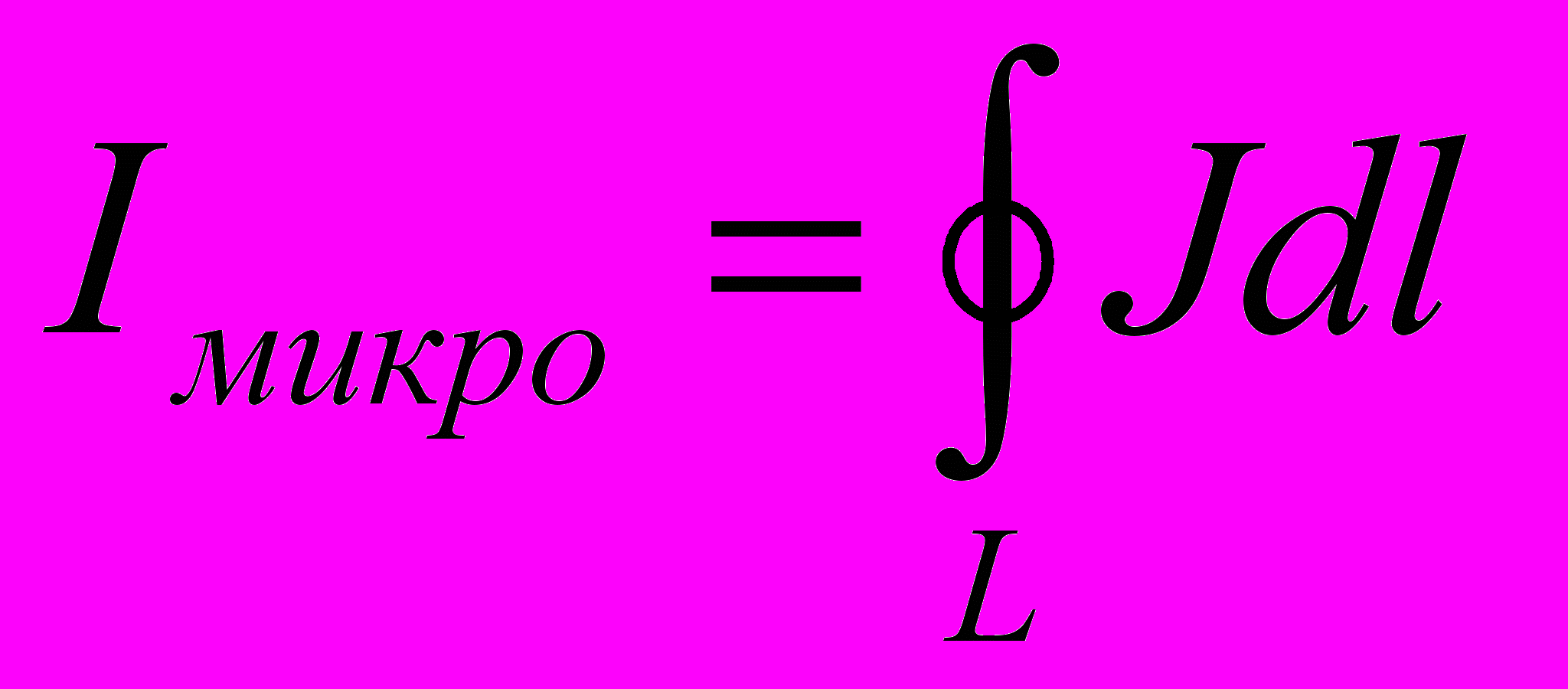
- Циркуляцию вектора магнитной индукции в веществе можно представить
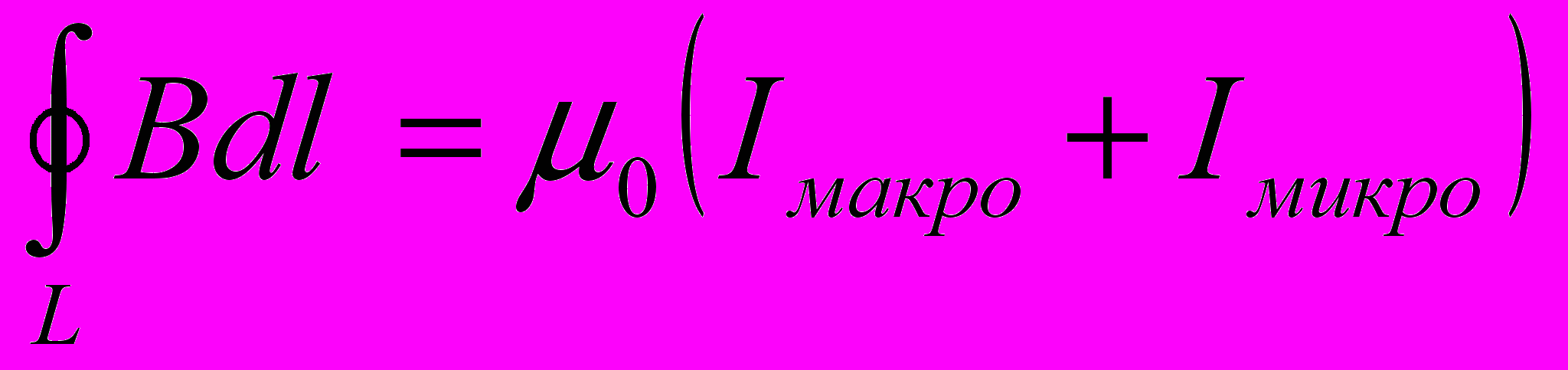
где Iмакро и Iмикро – алгебраические суммы сил макро и микротоков сквозь поверхность, ограниченную контуром замкнутым L.
- С учетом определения микротоков можно записать
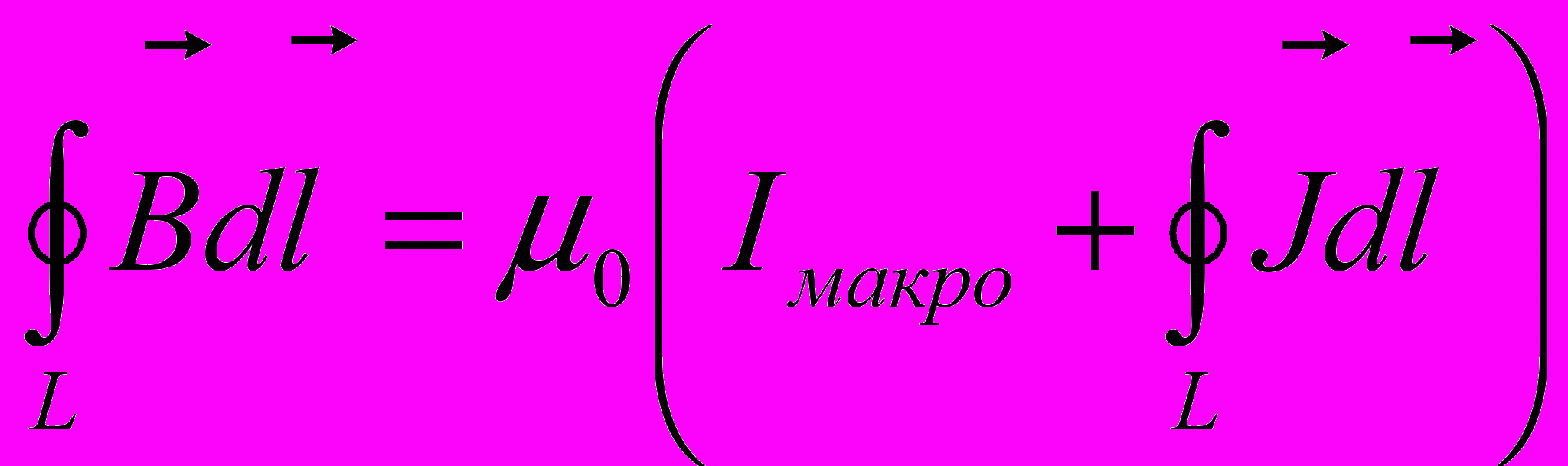

- Таким образом, закон полного тока для магнитного поля в веществе будет иметь вид
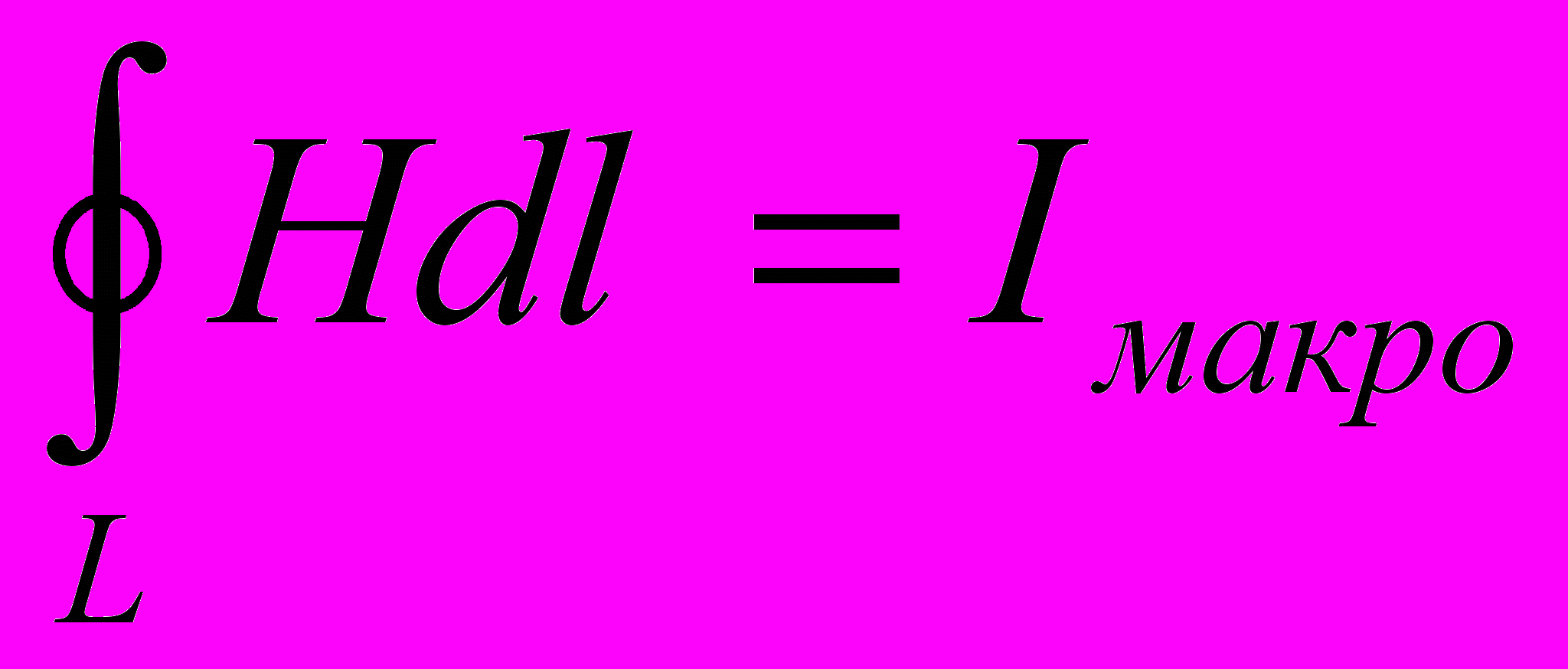
где
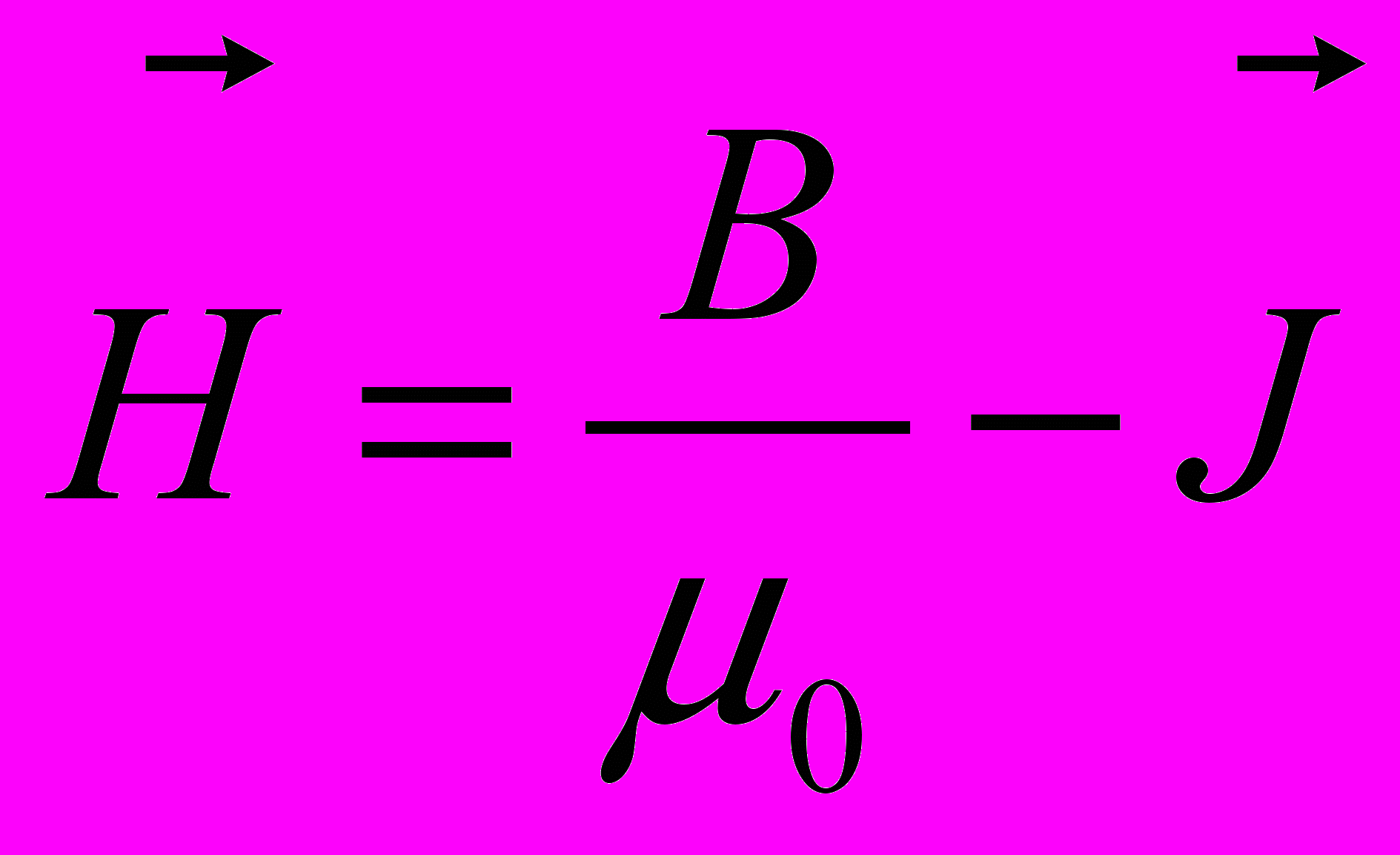 – напряженность магнитного поля
– напряженность магнитного поля- Учитывая, что намагниченность зависит от магнитной индукции внешнего магнитного поля
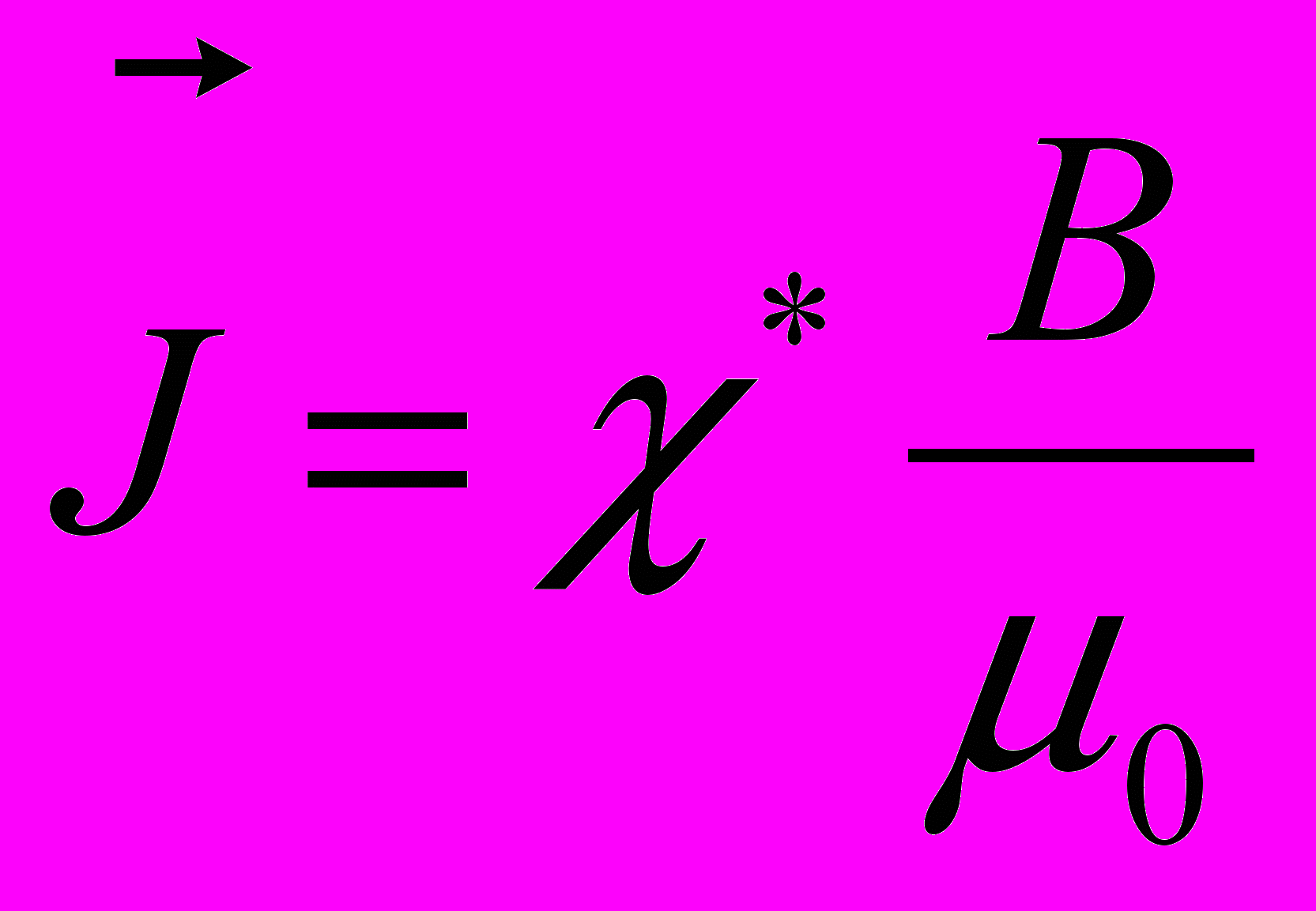
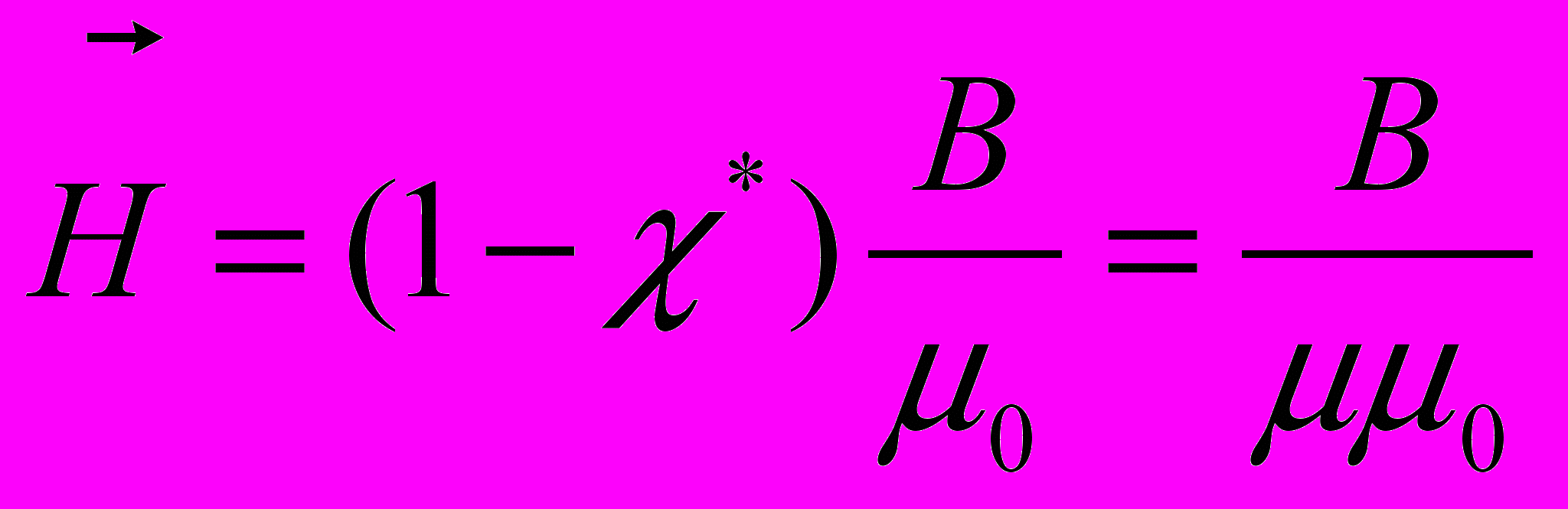
где =1+ - относительная магнитная проницаемость вещества.
- С напряженностью магнитного поля намагниченность изотропной среды связана соотношением
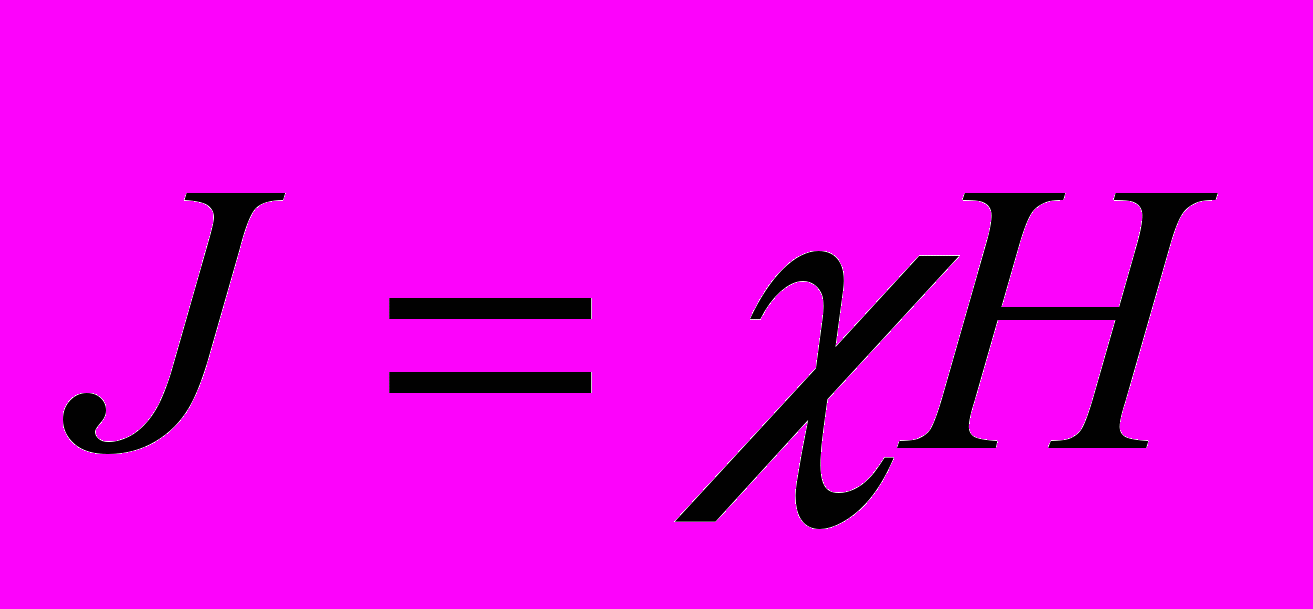
-
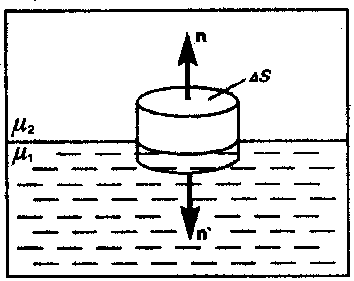
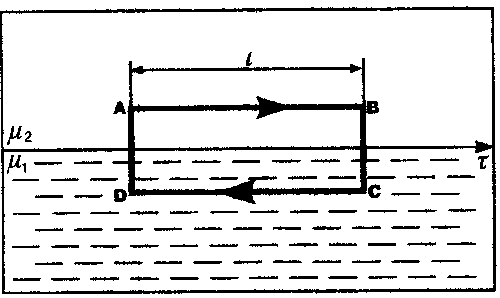
На границе раздела двух однородных магнетиков с относительными магнитными проницаемостями 1 и 2 при отсутствии тока проводимости характеристики магнитного поля меняются.
- Согласно теореме Остроградского-Гаусса
- Согласно теореме Остроградского-Гаусса
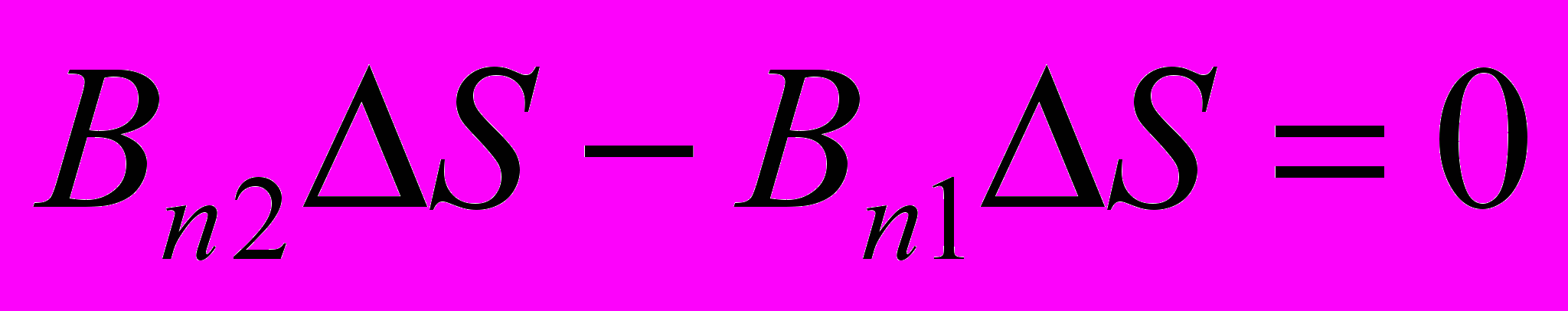 и
и 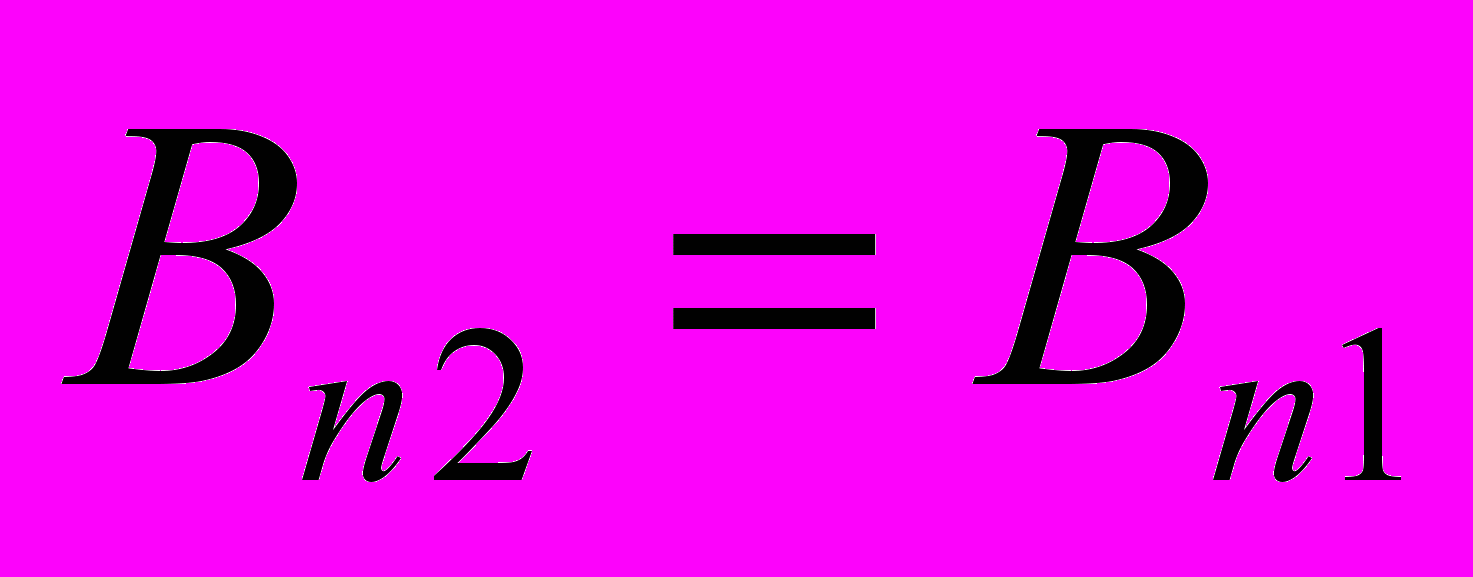
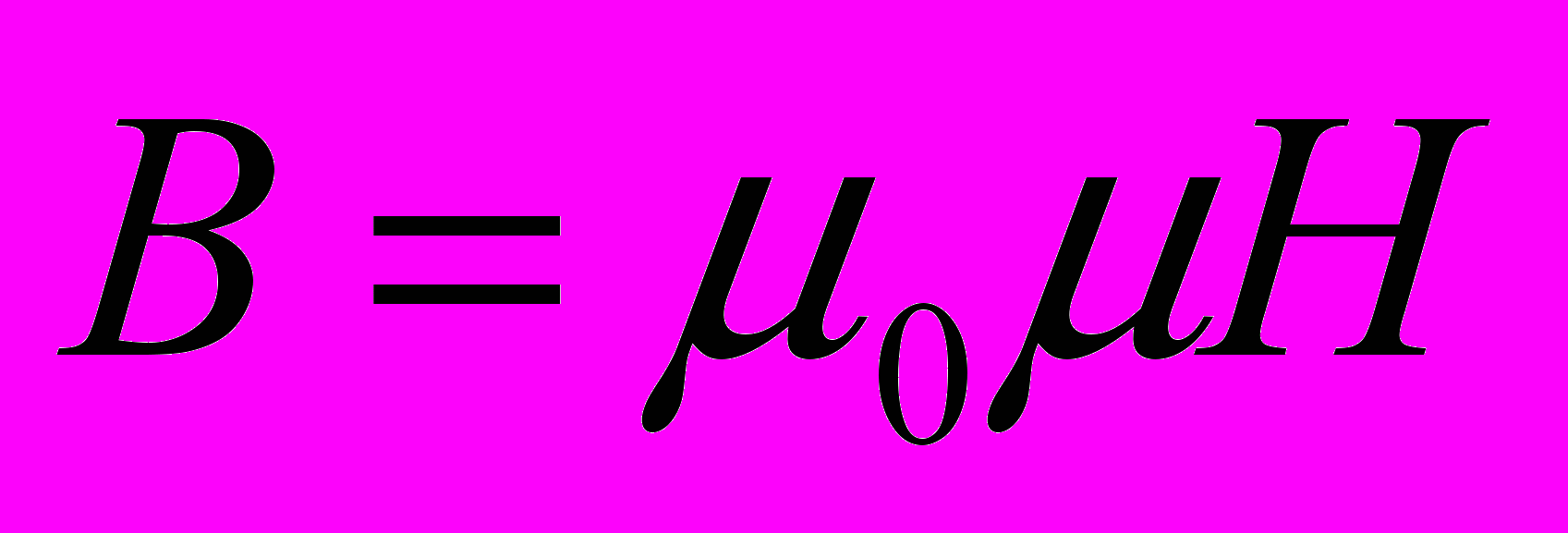
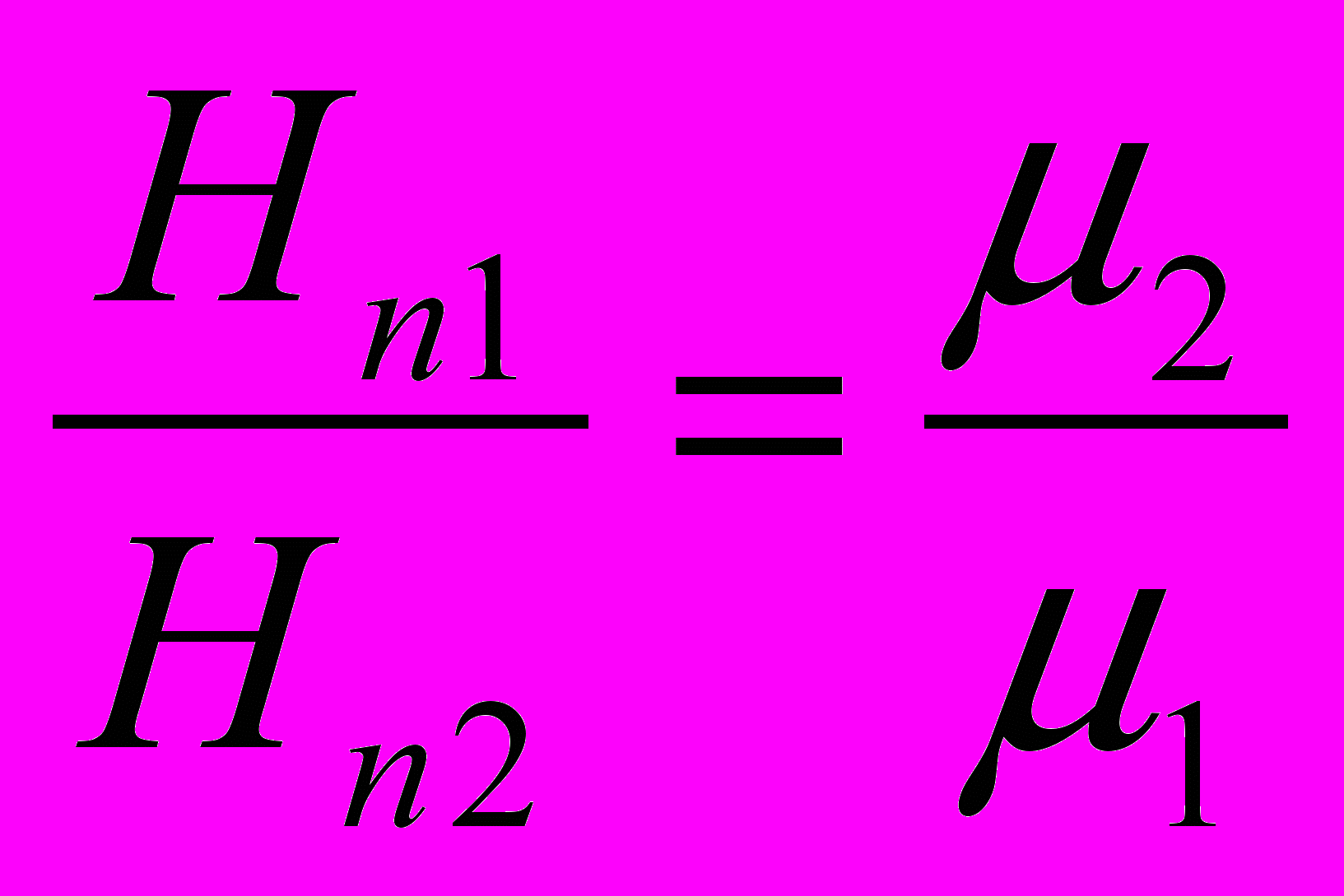
- Согласно теореме о циркуляции вектора Н
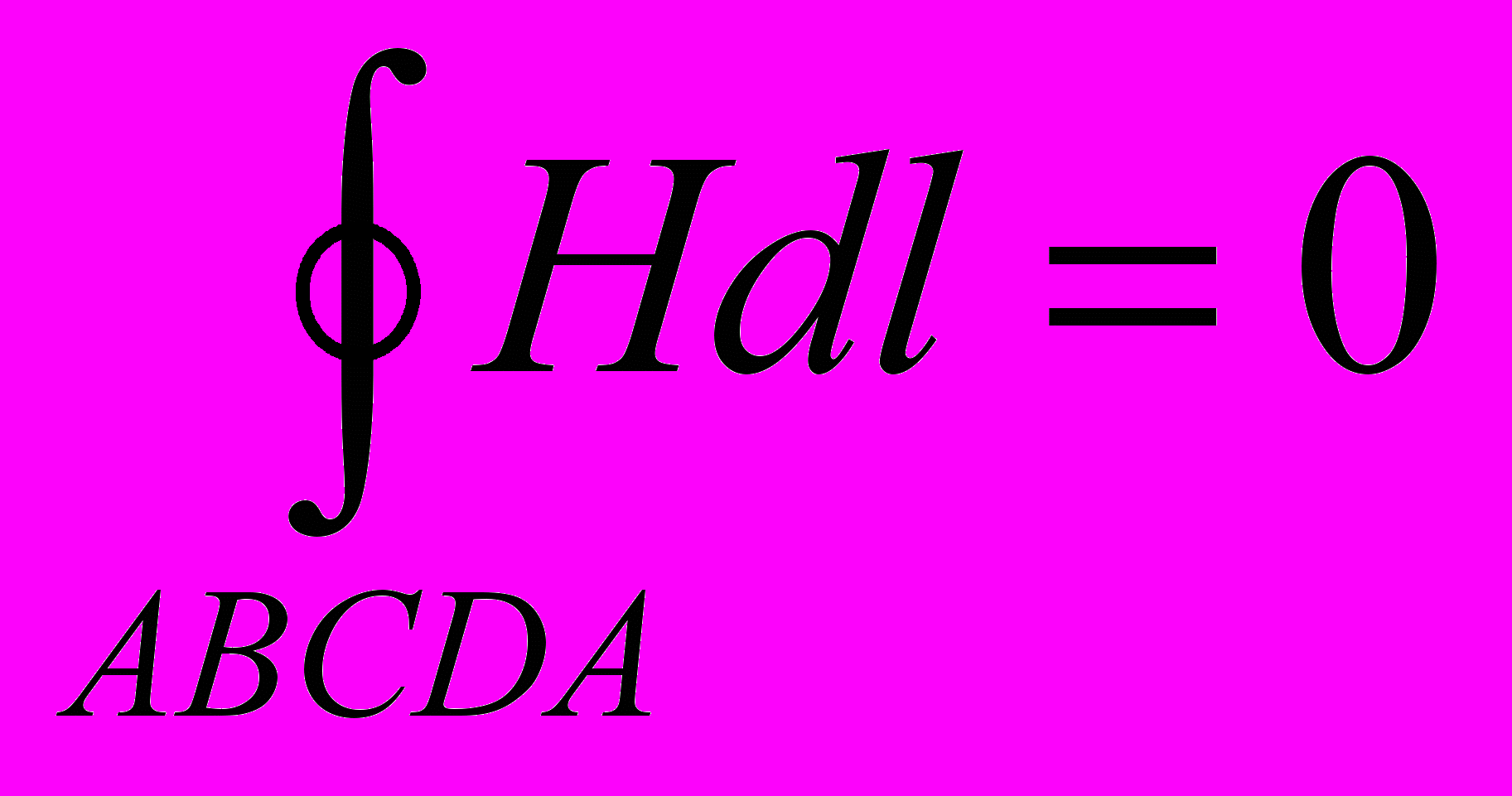
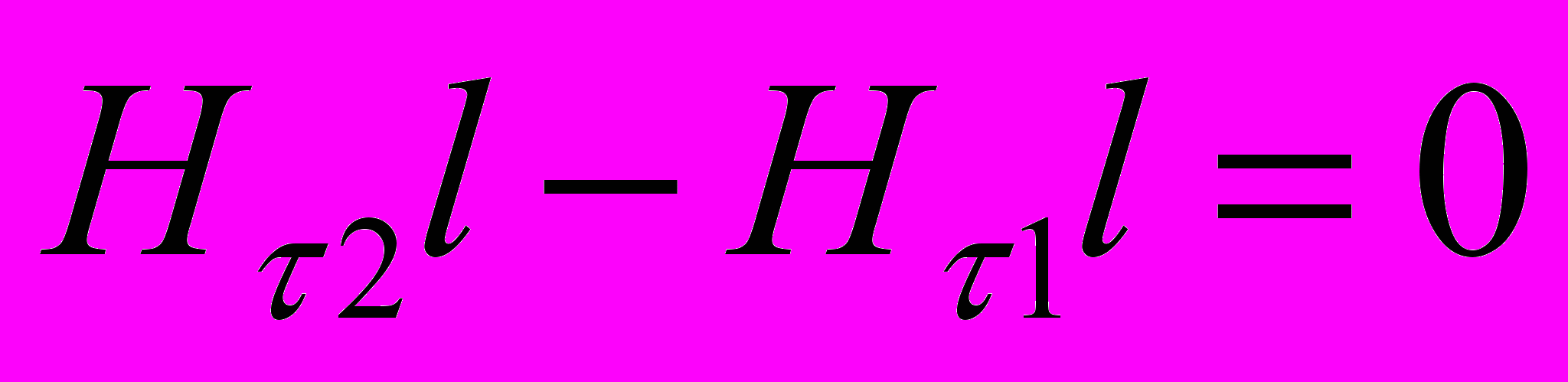
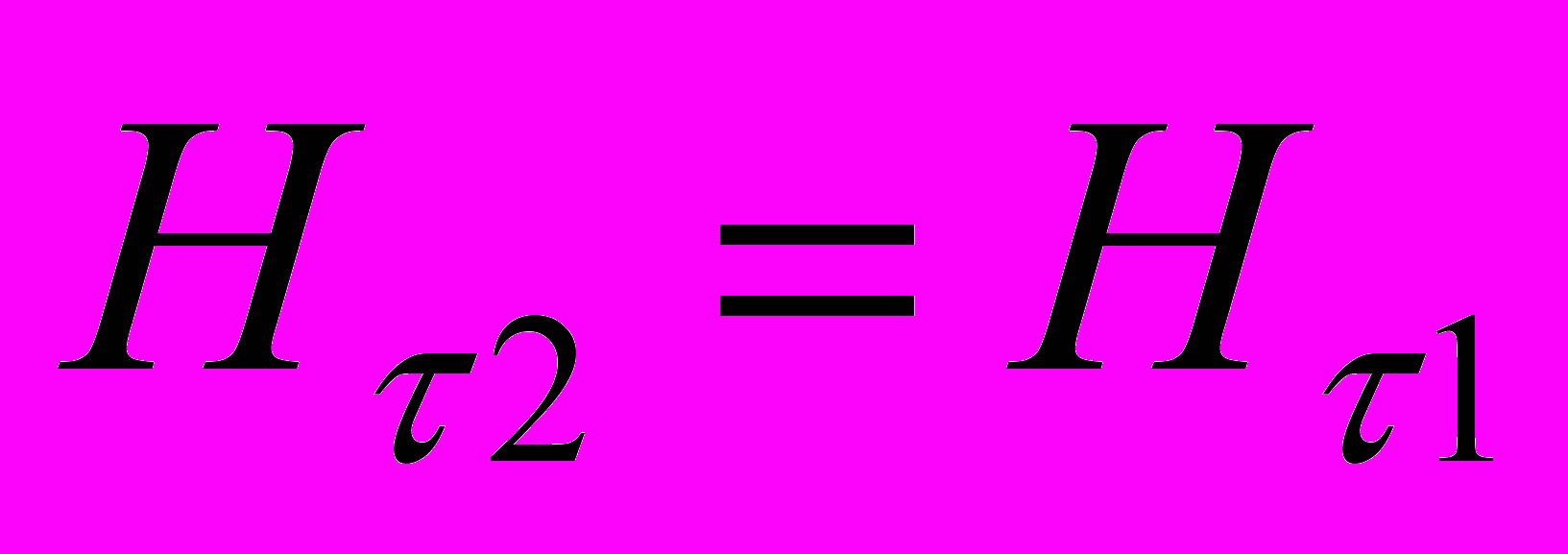
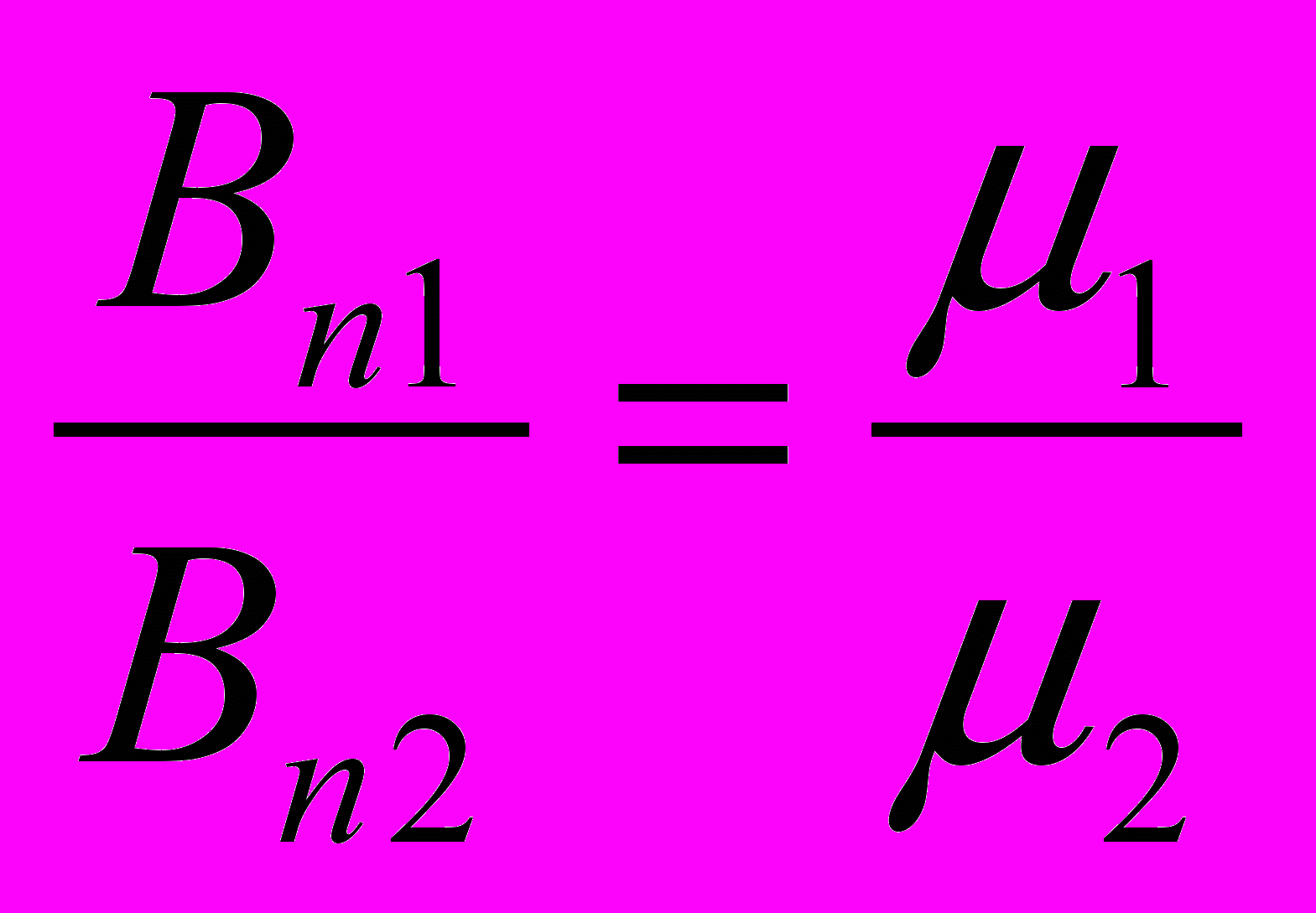
- При переходе через границу нормальная составляющая В и тангенциальная составляющая Н изменяются непрерывно, а нормальная составляющая Н и тангенциальная составляющая В испытывают скачок. При пересечении границы под углом линии преломляются
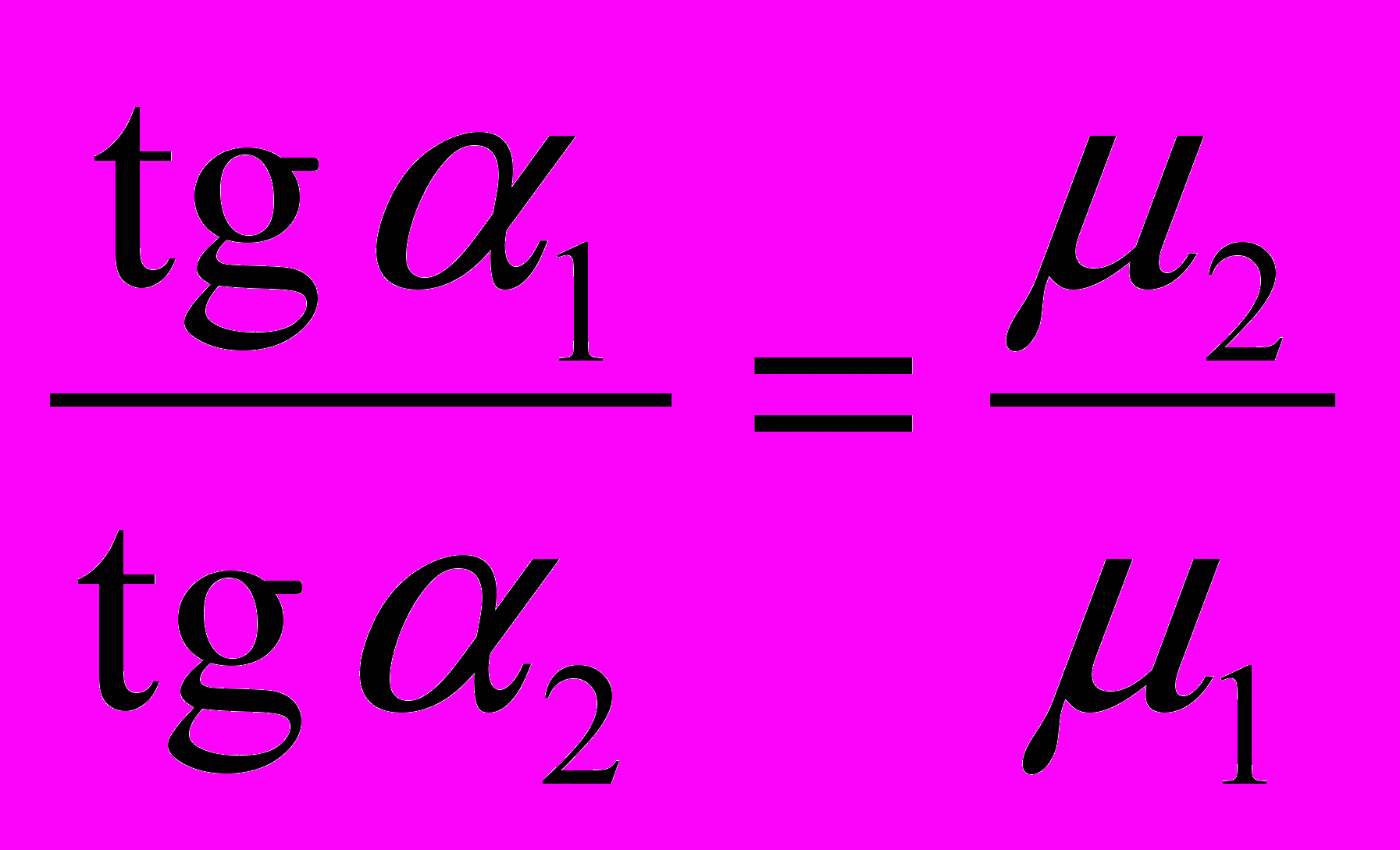
- Магнитной цепью называется последовательность тел, через которые проходят линии магнитной индукции.
- Закон Ома для неразветвленной замкнутой магнитной цепи
- Закон Ома для неразветвленной замкнутой магнитной цепи
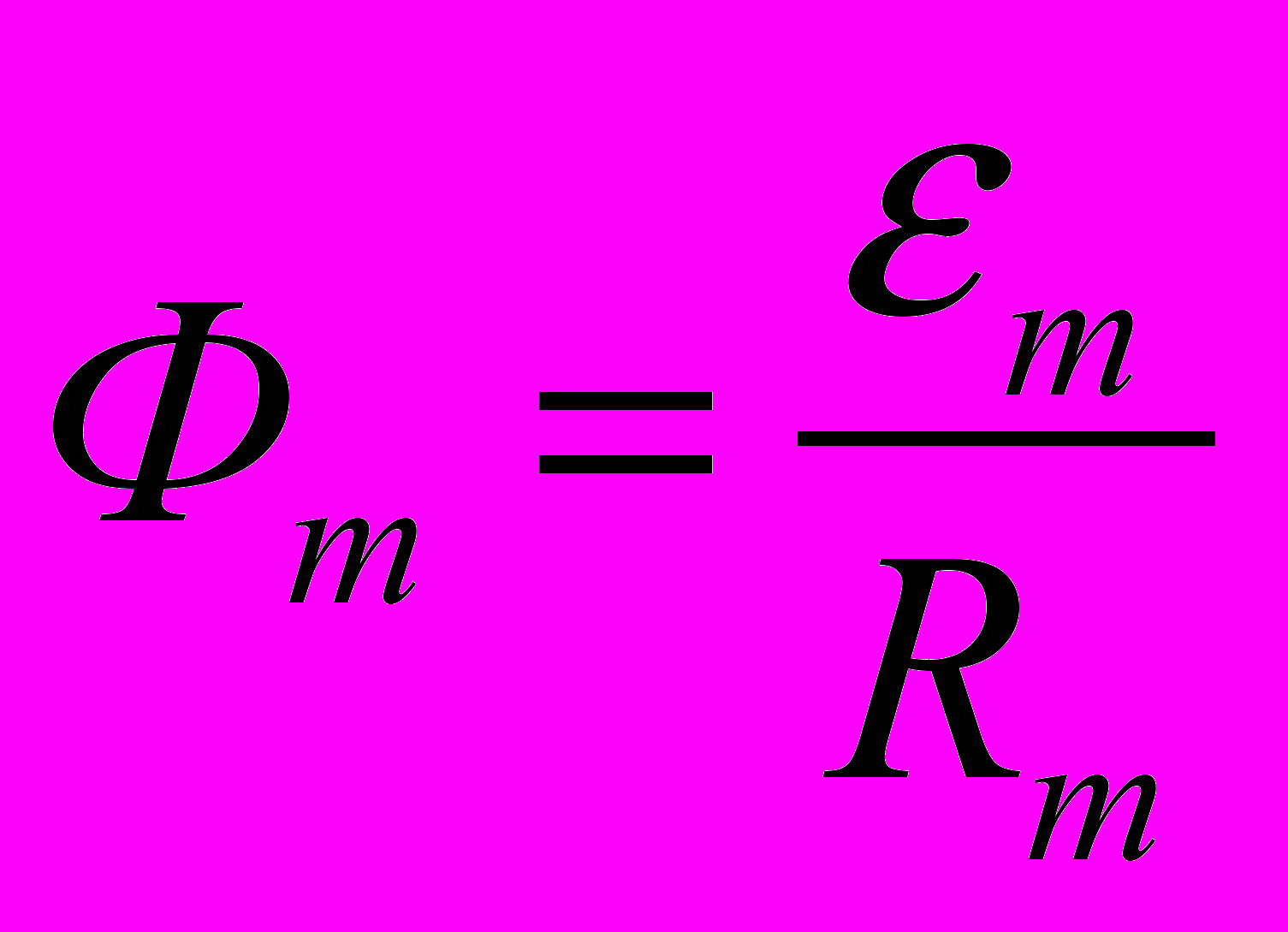
где Фm – магнитный поток через поперечное сечение магнитной цепи, Rm – полное магнитное сопротивление магнитной цепи, m – магнитодвижущая сила, равная циркуляции вектора напряженности магнитного поля вдоль рассматриваемой замкнутой магнитной цепи (контур L)
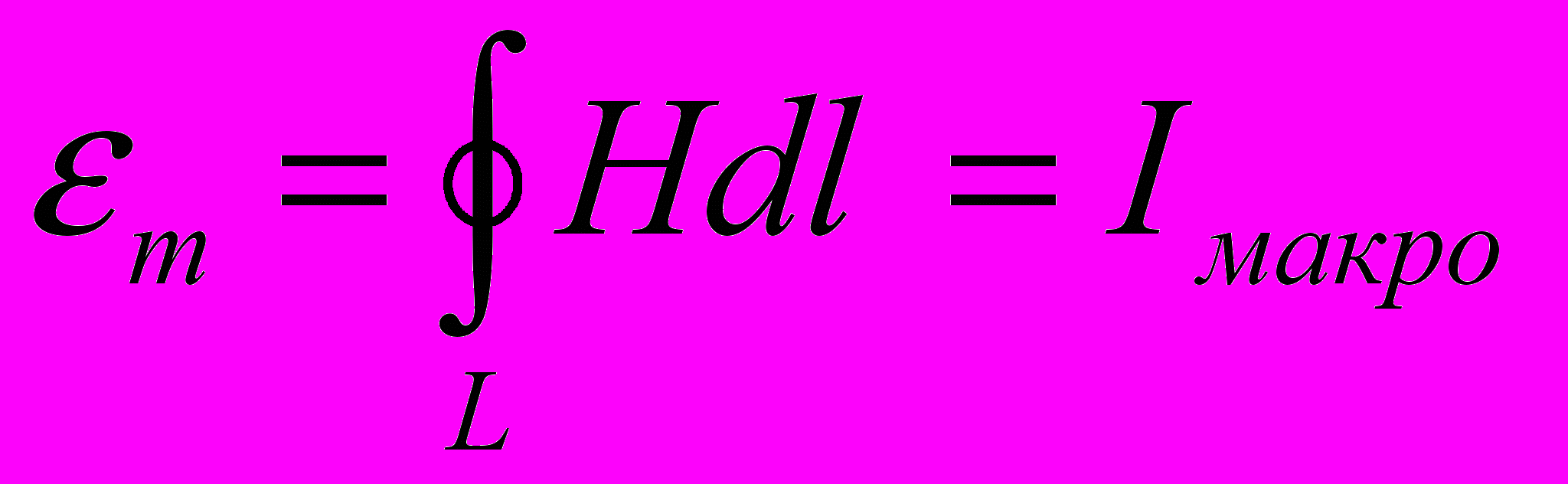
* Пример: Если на магнитную цепь навита обмотка из N витков, то
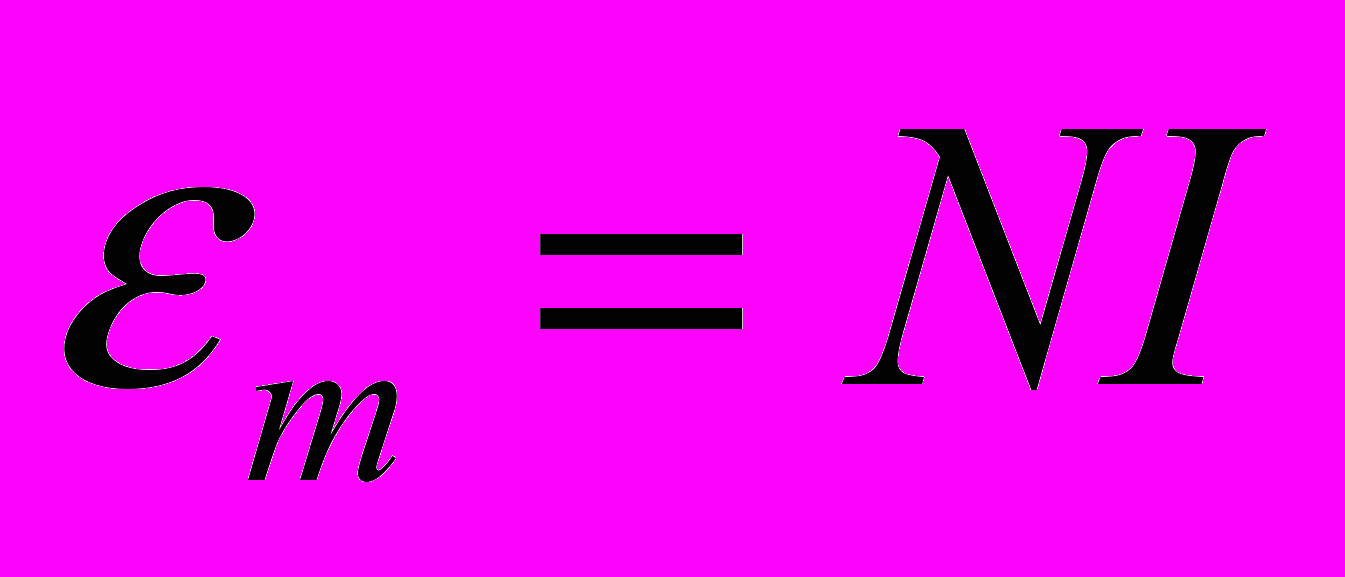
- Магнитное сопротивление однородного участка магнитной цепи
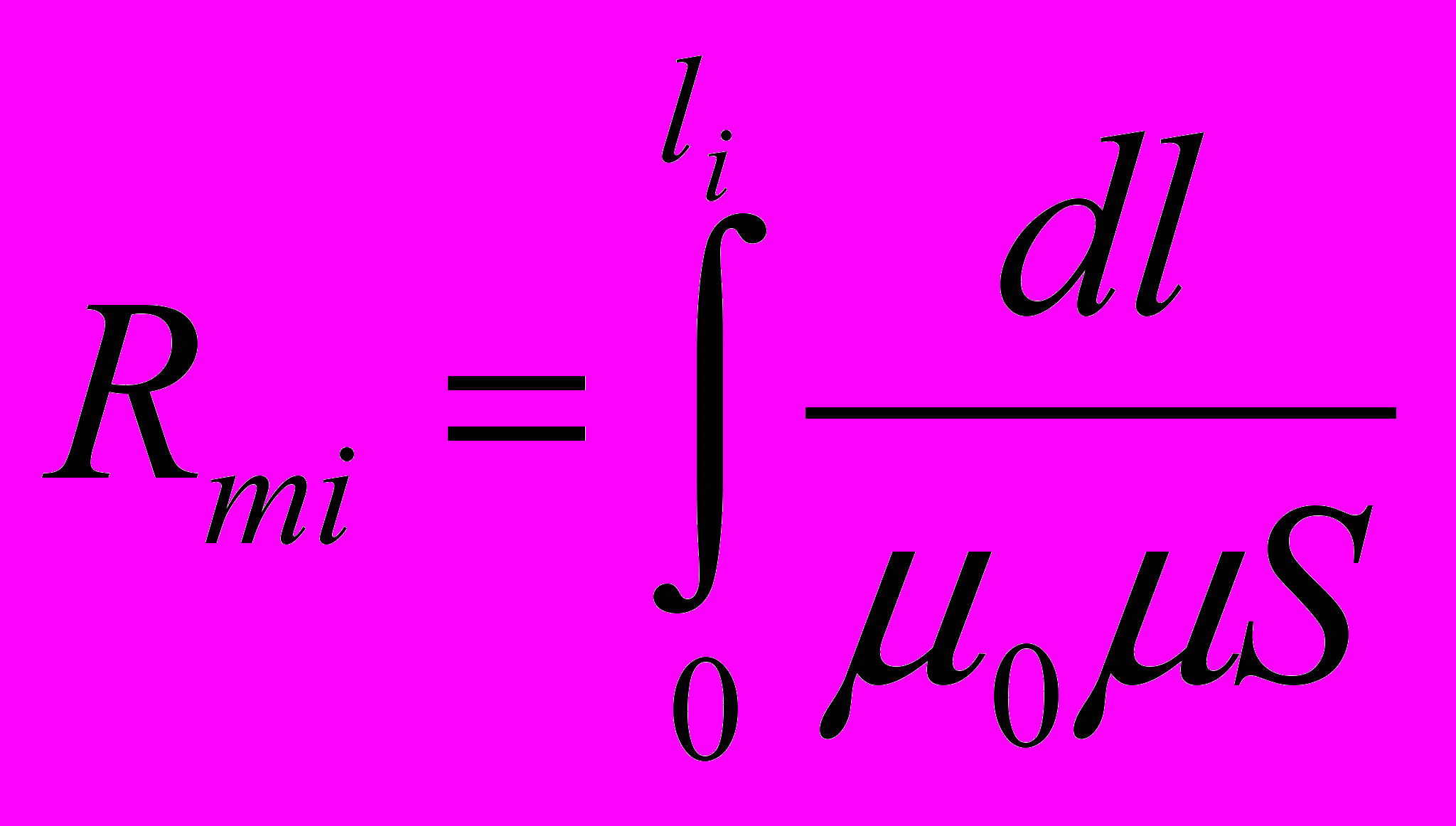
* Пример: Если площадь поперечного сечения участка цепи постоянна, то
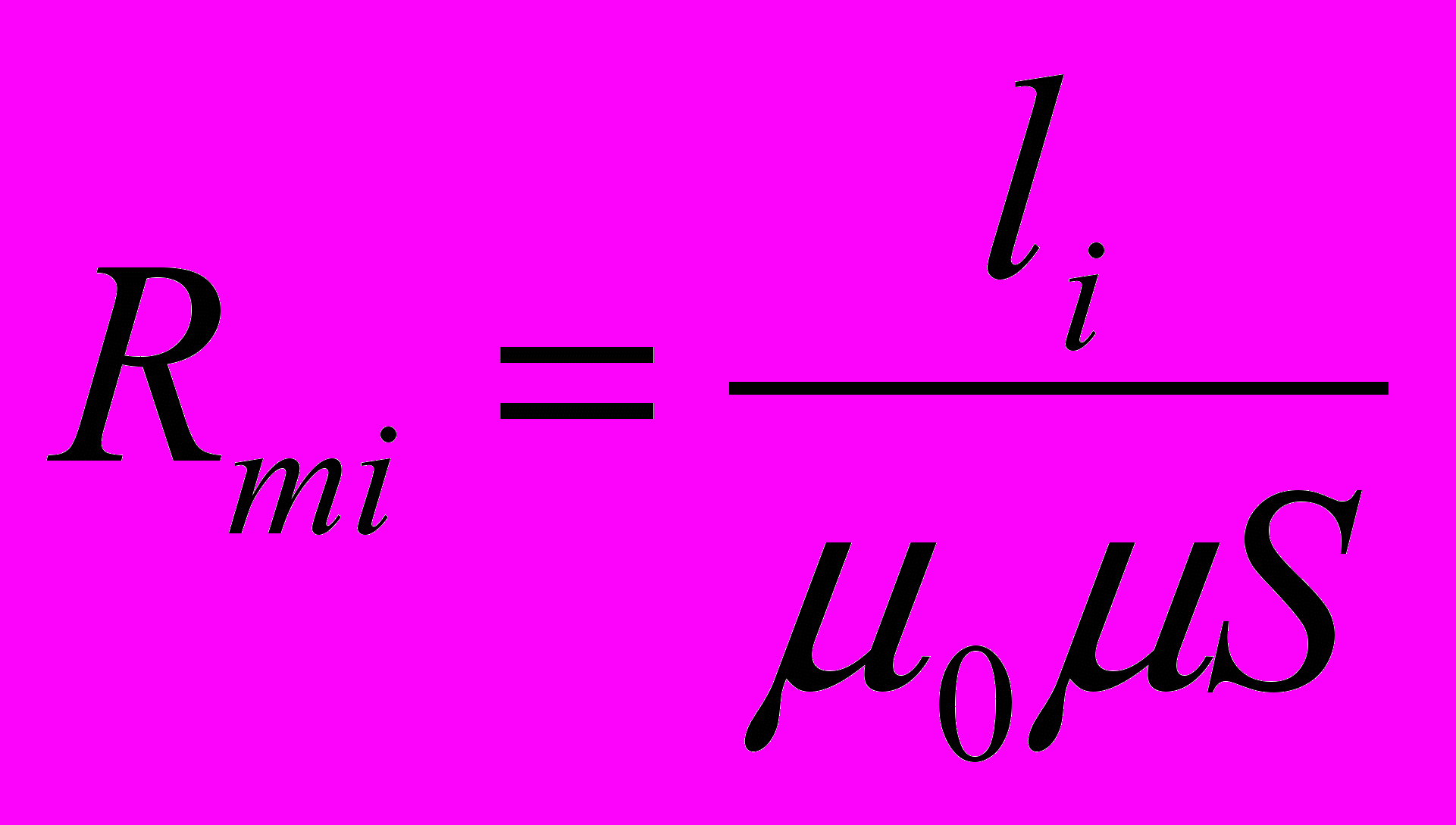
Магнитное сопротивление последовательно соединенных n участков магнитной цепи
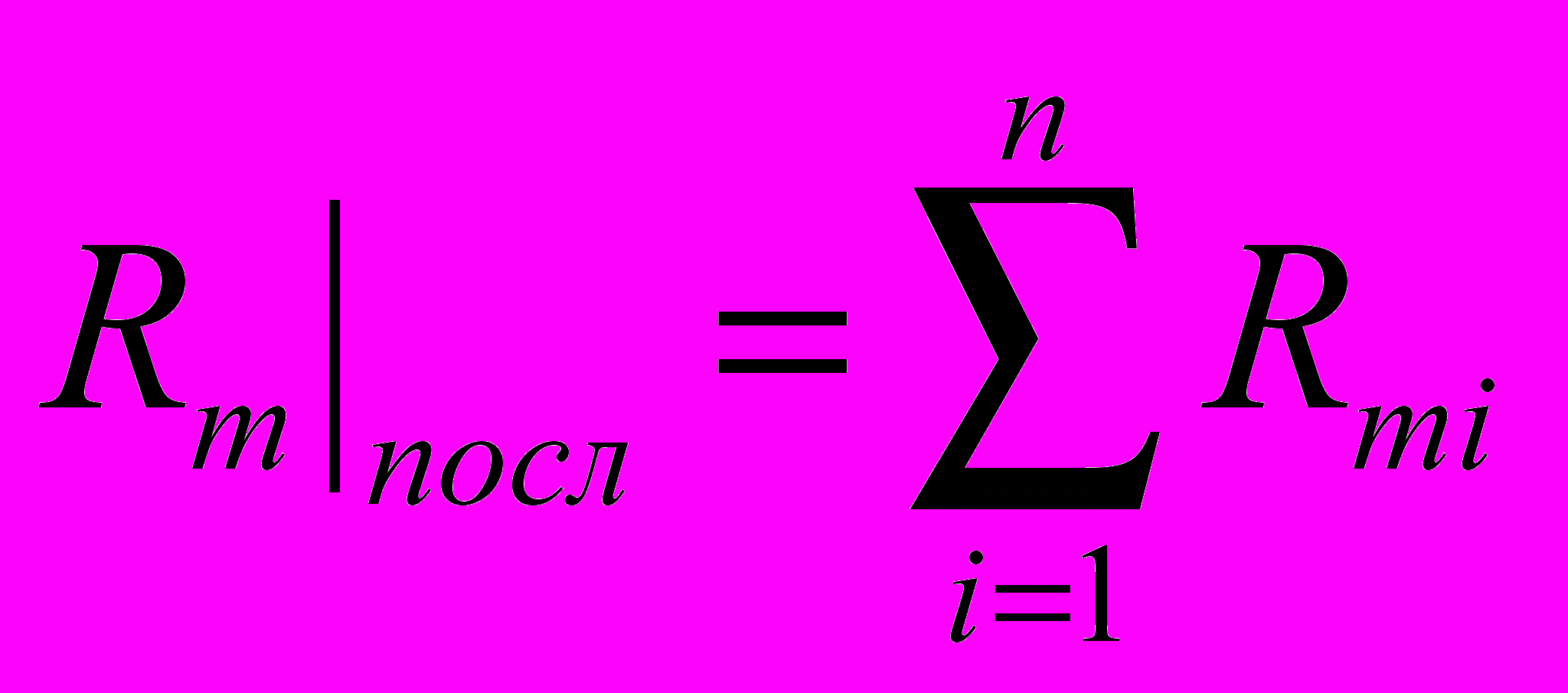
Магнитное сопротивление параллельно соединенных n участков магнитной цепи
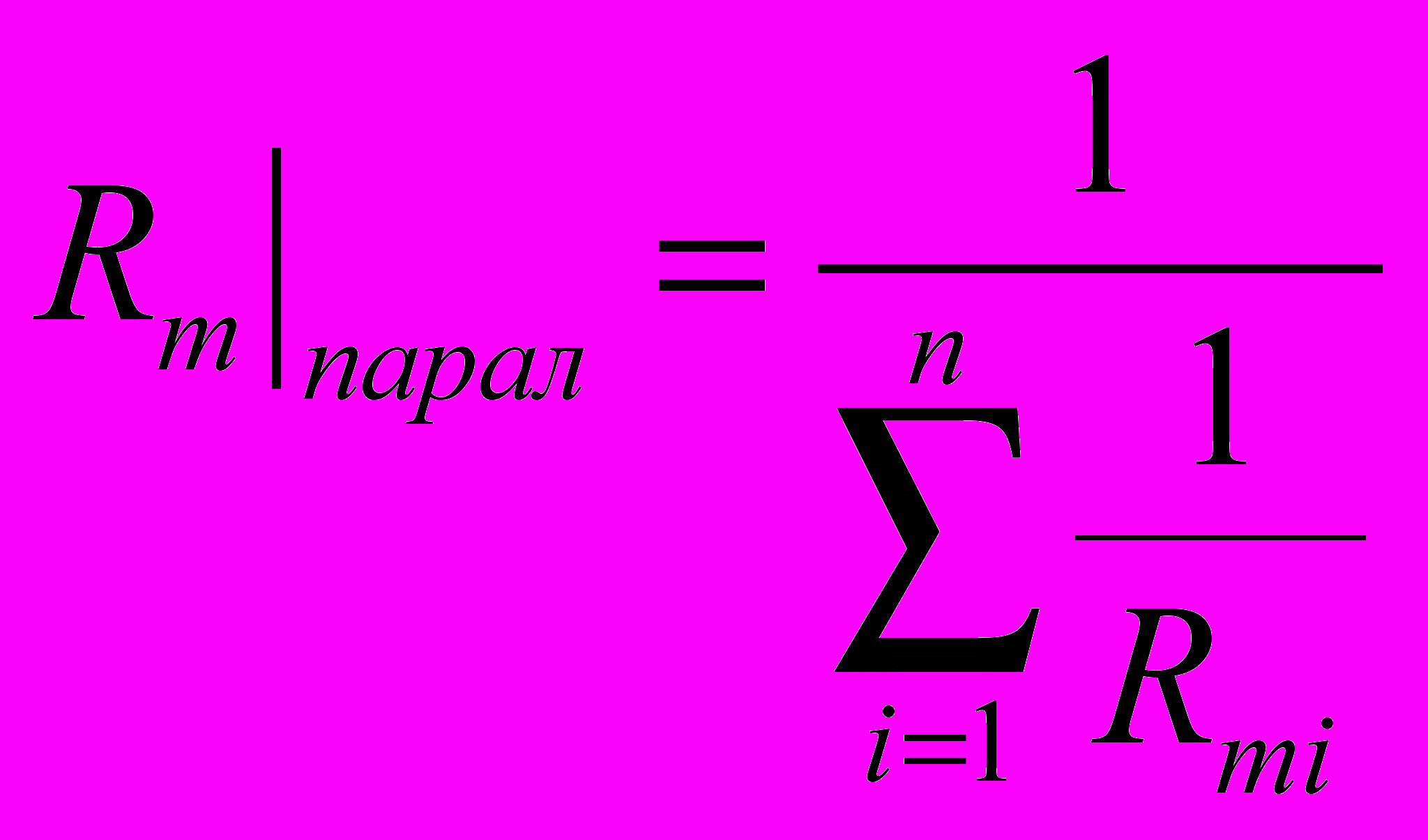
- Узлом магнитной цепи называется место ее разветвления
- Алгебраическая сумма магнитных потоков во всех n участках, сходящихся в узле, равна нулю (первое правило Кирхгофа – вытекает из теоремы Остроградского-Гаусса)
- Алгебраическая сумма магнитных потоков во всех n участках, сходящихся в узле, равна нулю (первое правило Кирхгофа – вытекает из теоремы Остроградского-Гаусса)
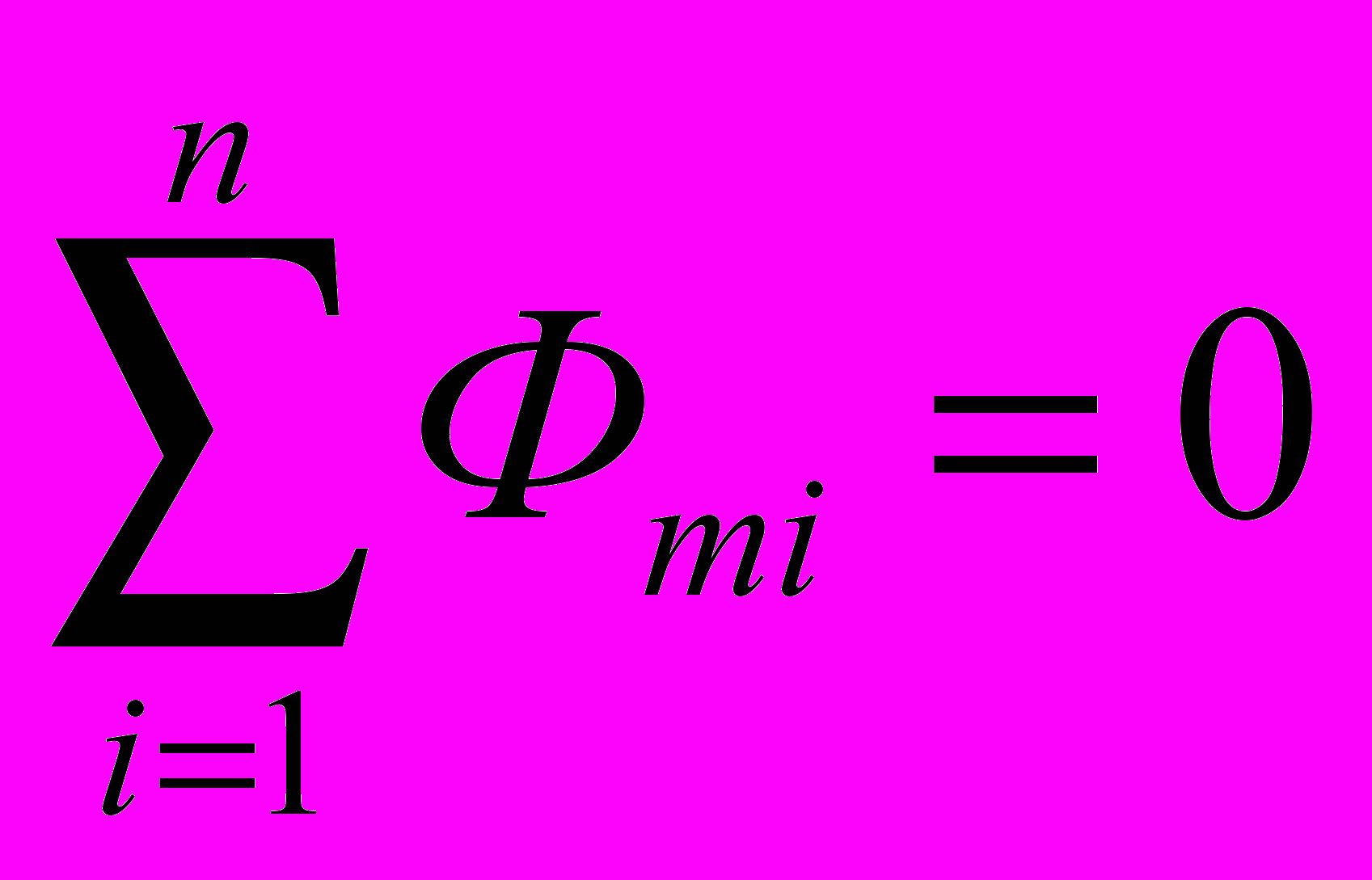
- В любой замкнутой магнитной цепи, произвольно выбранной в разветвленной магнитной цепи, алгебраическая сумма произведений магнитных потоков на магнитные сопротивления соответствующих участков цепи равна алгебраической сумме магнитодвижущих сил в этой цепи
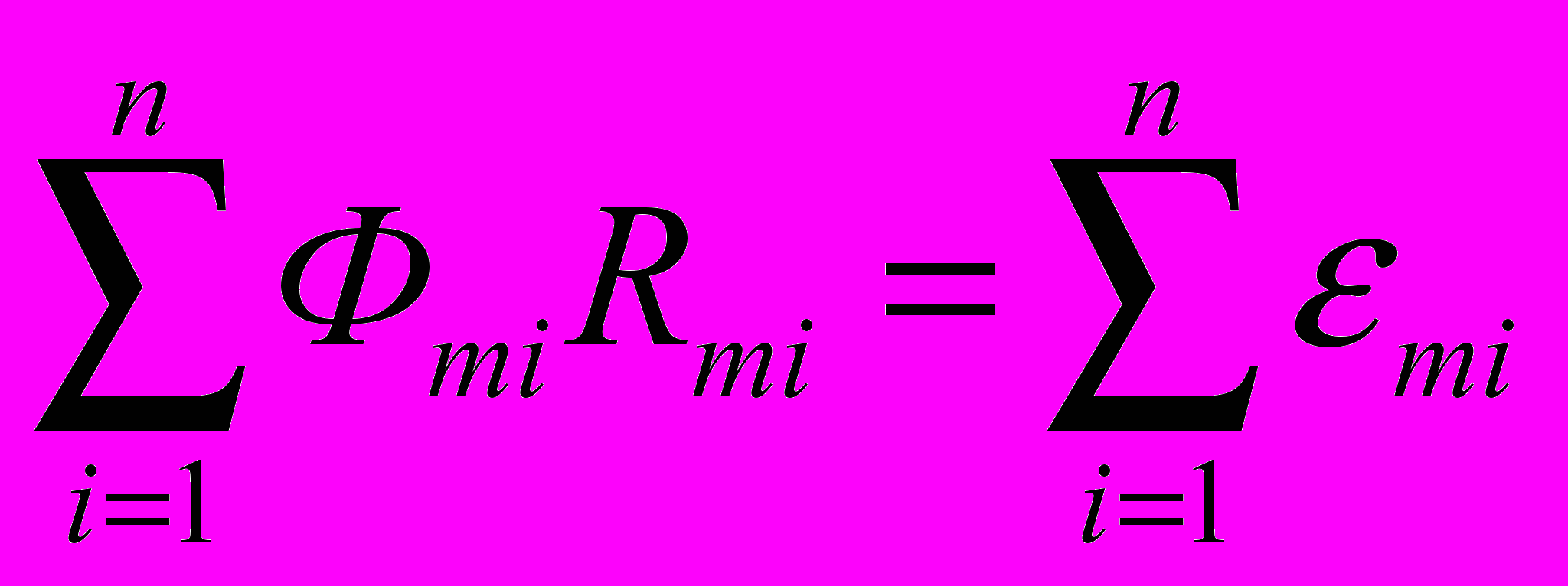
- Энергия магнитного поля в магнетике, для которого соблюдается линейная зависимость между J и В (диамагнетики и парамагнетики), может быть выражена
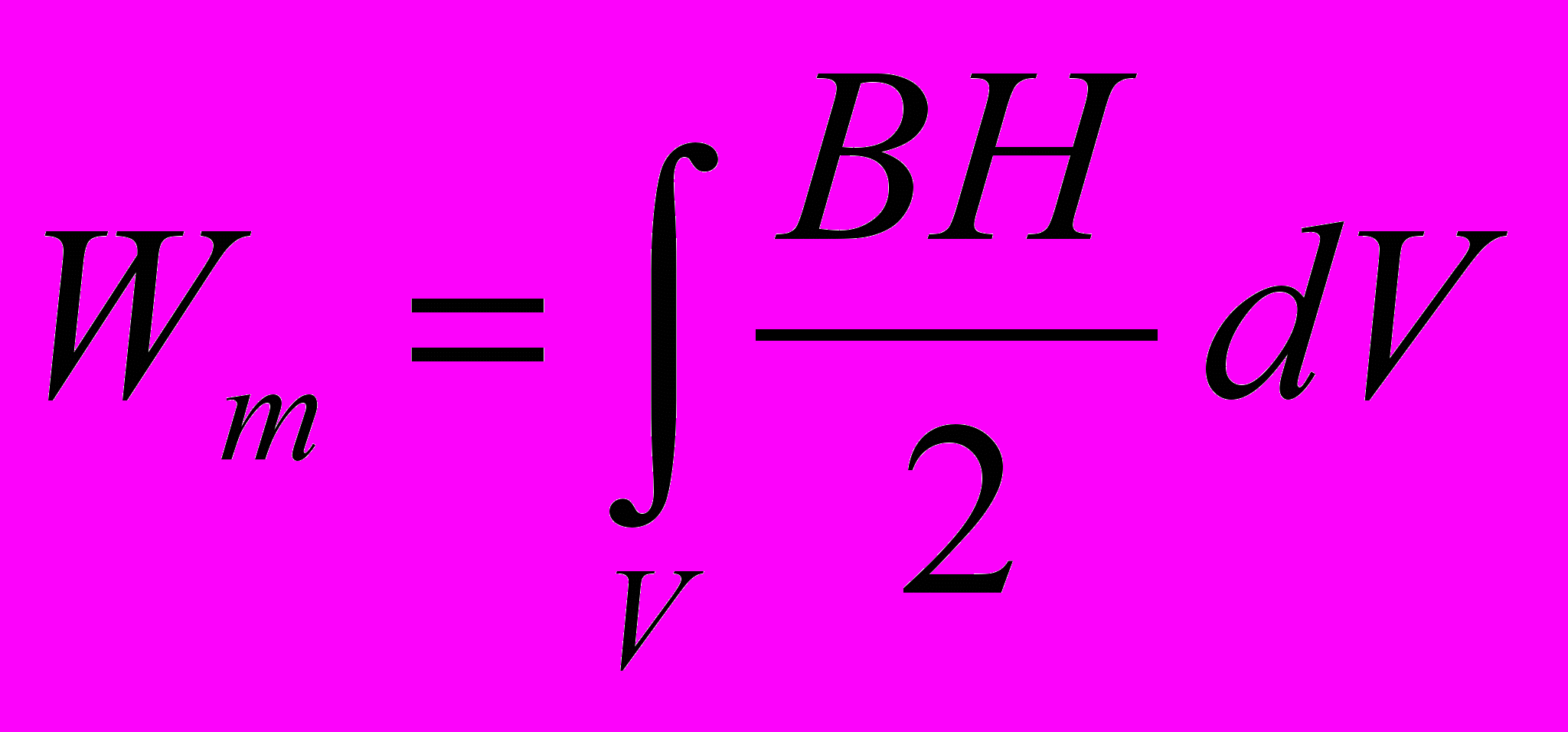
- Энергия магнитного поля произвольной системы из n контуров с токами может быть найдена также из выражения
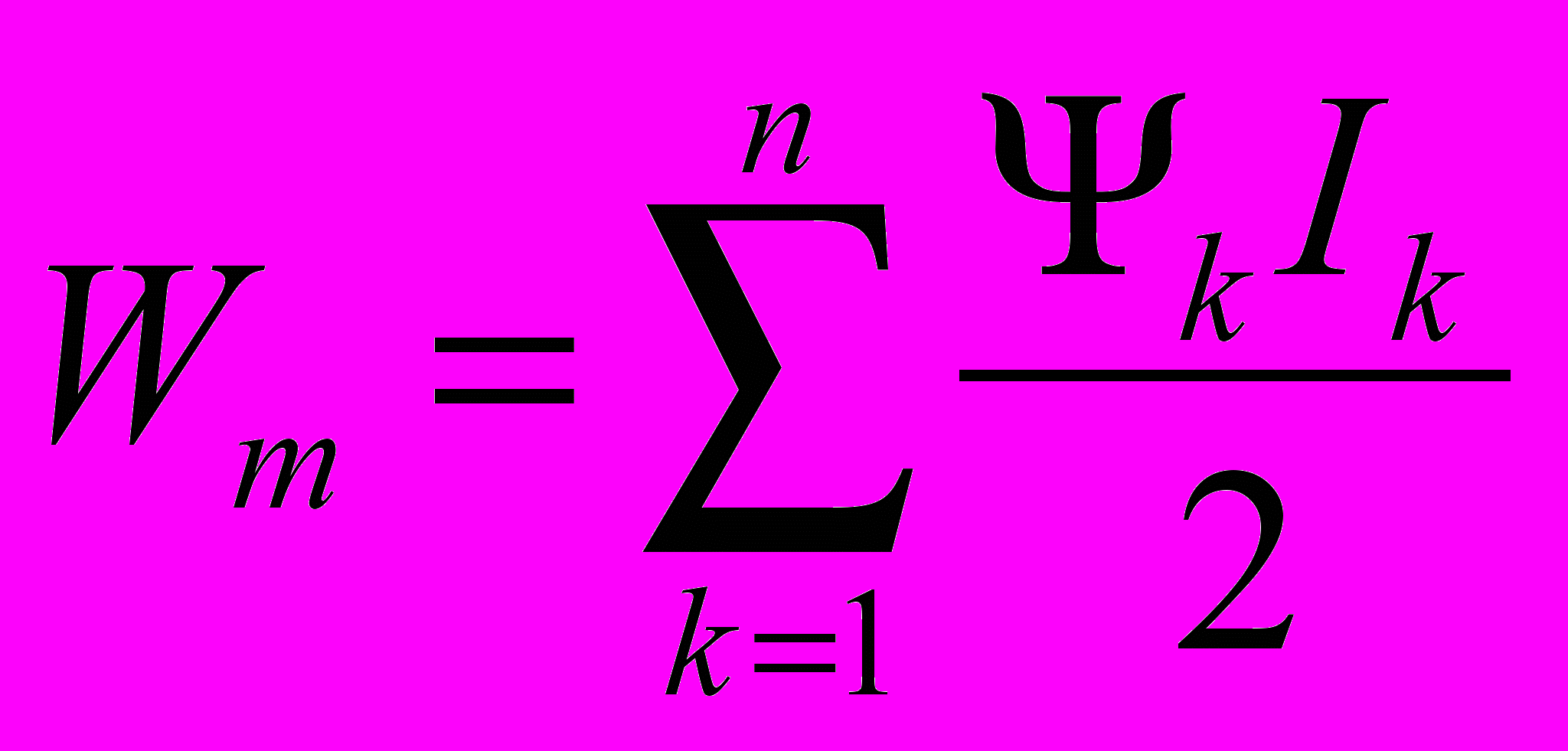
где
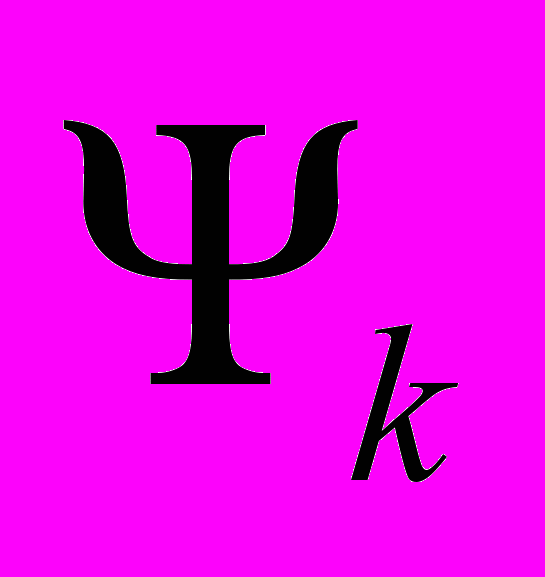 - потокосцепление k-го контура, которое содержит два слагаемых
- потокосцепление k-го контура, которое содержит два слагаемых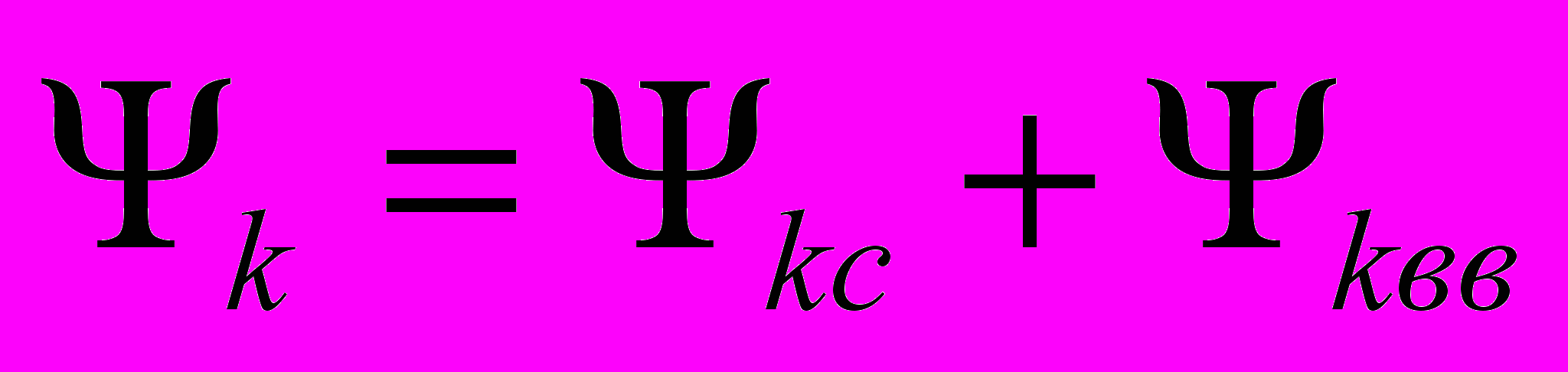
первое из которых представляет собой потокосцепление в k-ом контуре, а второе – потокосцепление k-го контура со всеми остальными контурами.
- Энергия магнитного поля будет равна
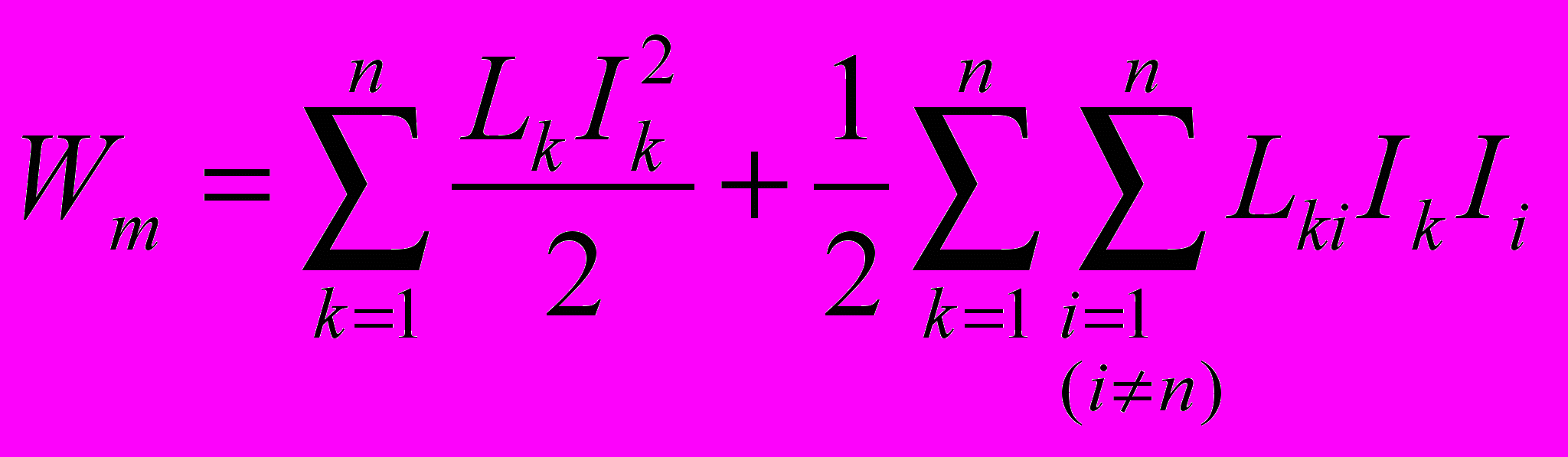
где первый член представляет собой сумму собственных энергий всех токов, а второй, называемый взаимной энергией токов, определяется взаимосвязью контуров системы (
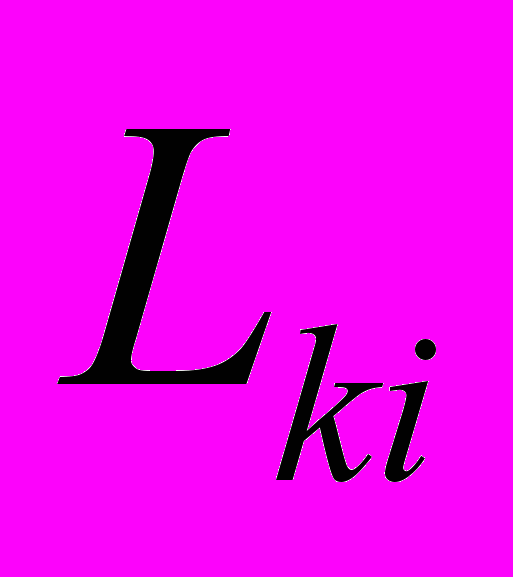 - взаимная индуктивность k-го и i-го контуров).
- взаимная индуктивность k-го и i-го контуров).- При малом изменении состояния системы закон сохранения энергии можно выразить в виде
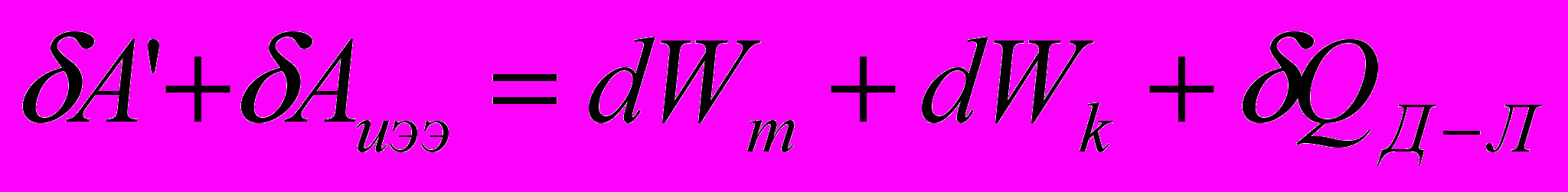
где
 – работа внешних сил в рассматриваемом процессе;
– работа внешних сил в рассматриваемом процессе; 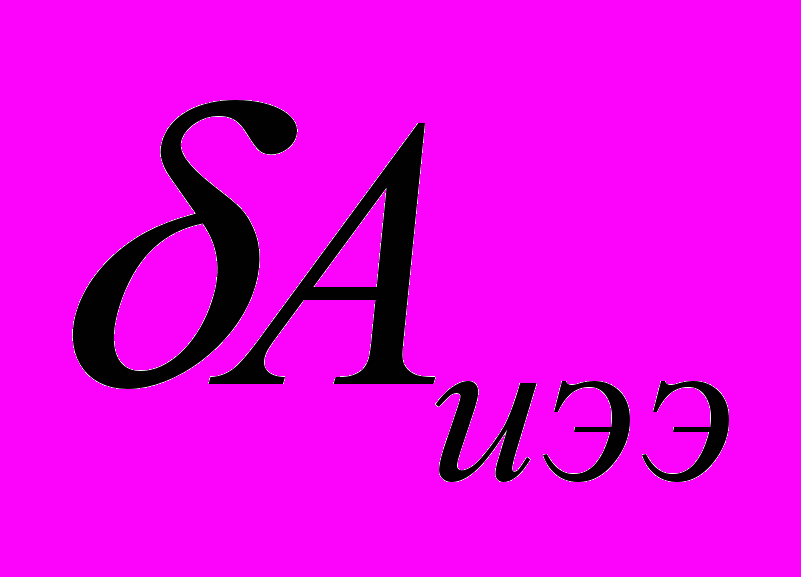 – работа источников электрической энергии;
– работа источников электрической энергии; 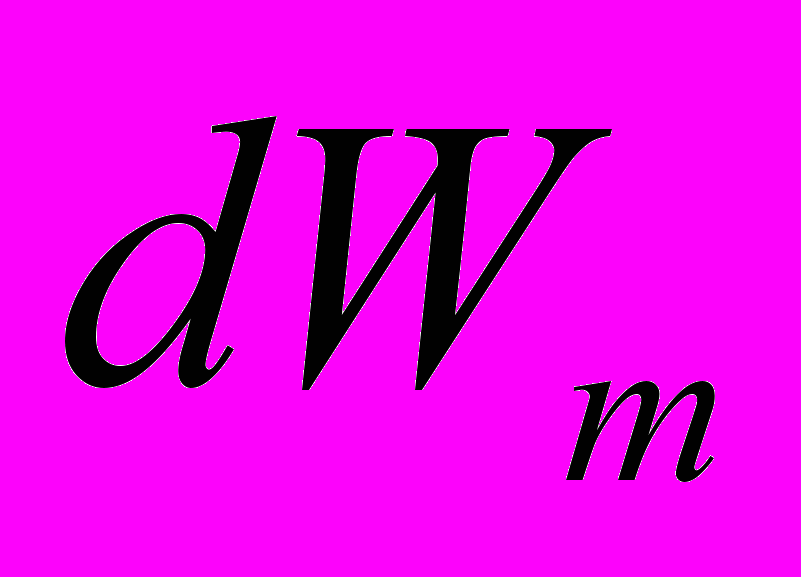 – изменение энергии магнитного поля;
– изменение энергии магнитного поля; 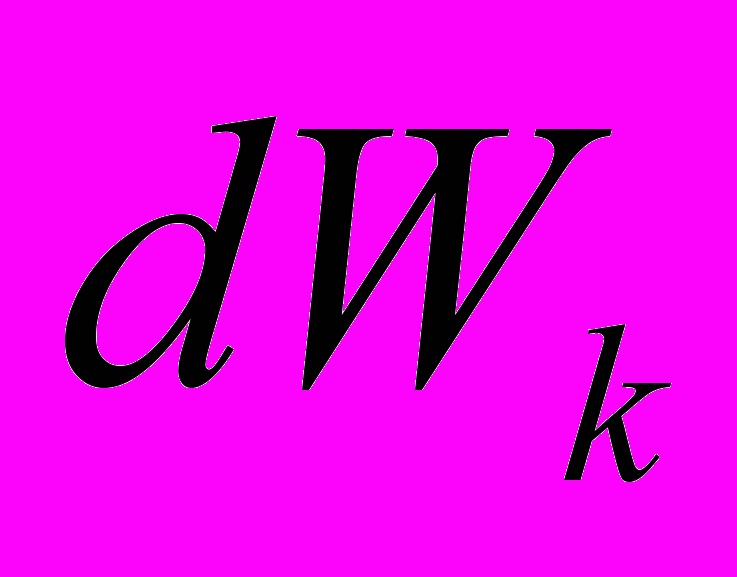 – изменение кинетической энергии системы;
– изменение кинетической энергии системы; 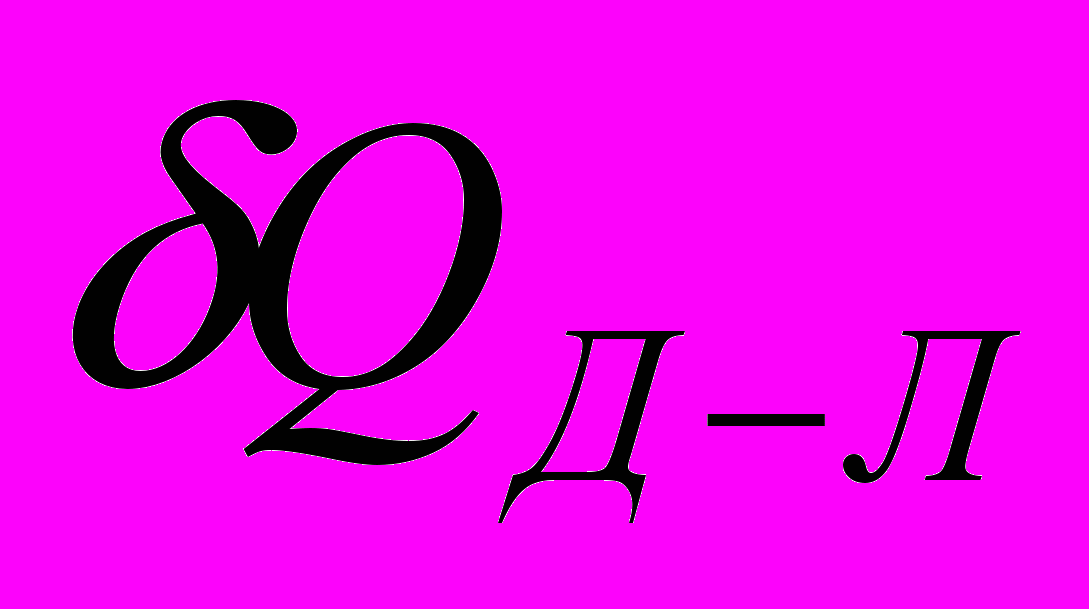 – теплота Джоуля-Ленца. (Изменением энергии электрического поля можно пренебречь из-за малой емкости проводников системы)
– теплота Джоуля-Ленца. (Изменением энергии электрического поля можно пренебречь из-за малой емкости проводников системы)- Если система квазистатическая (можно пренебречь изменением кинетической энергии), а работа внешних сил (пондемоторных) равна работе сил, действующих на тела системы
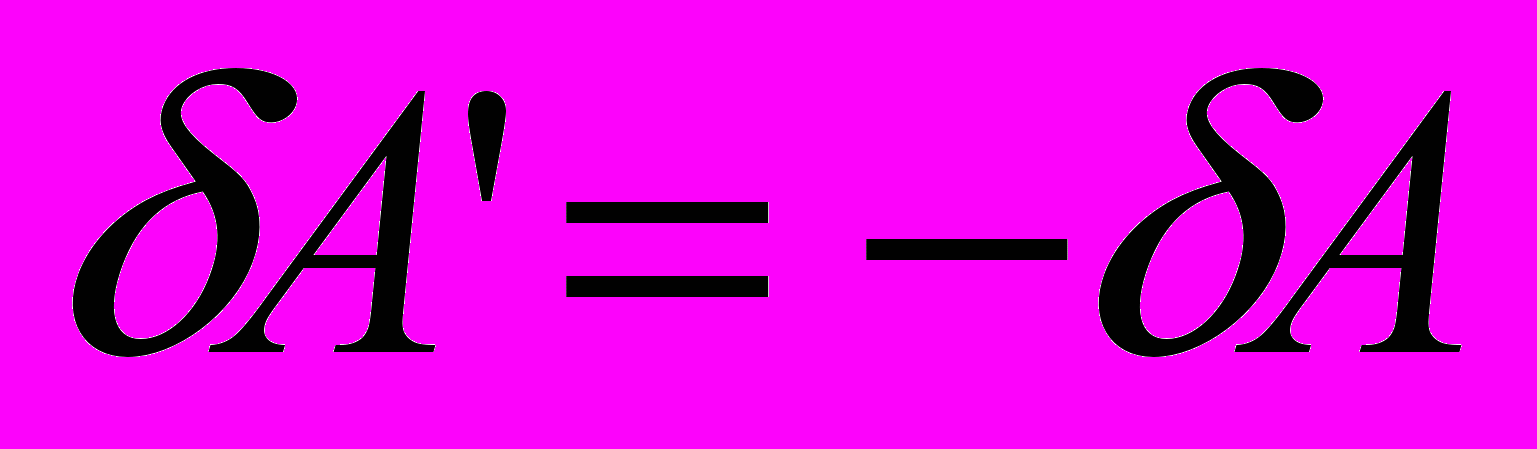 , то
, то
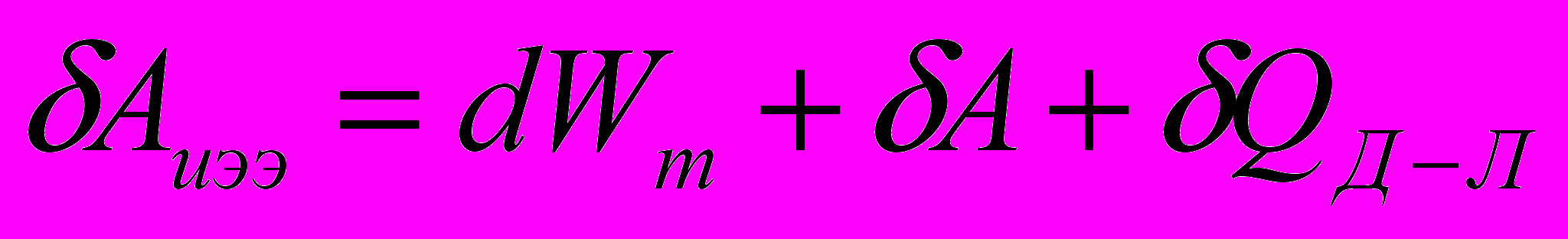
где
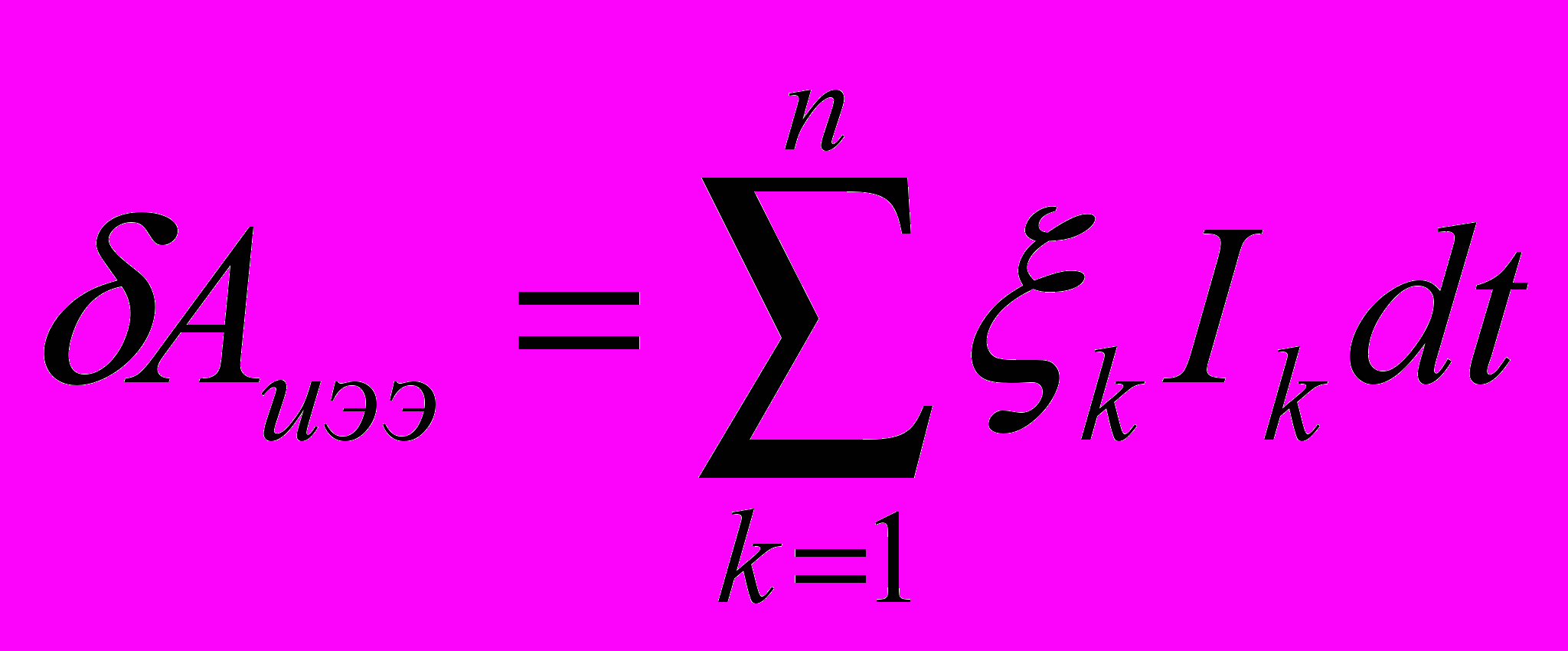 и
и 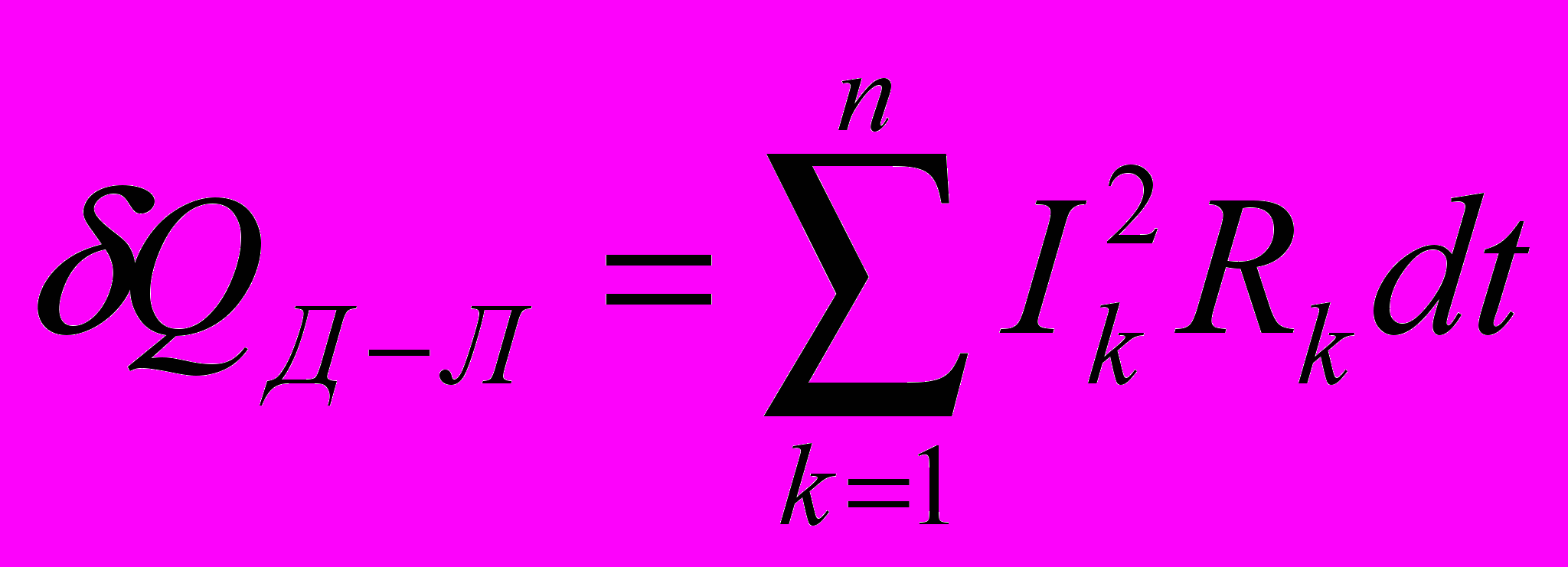
- Для неподвижного контура с током
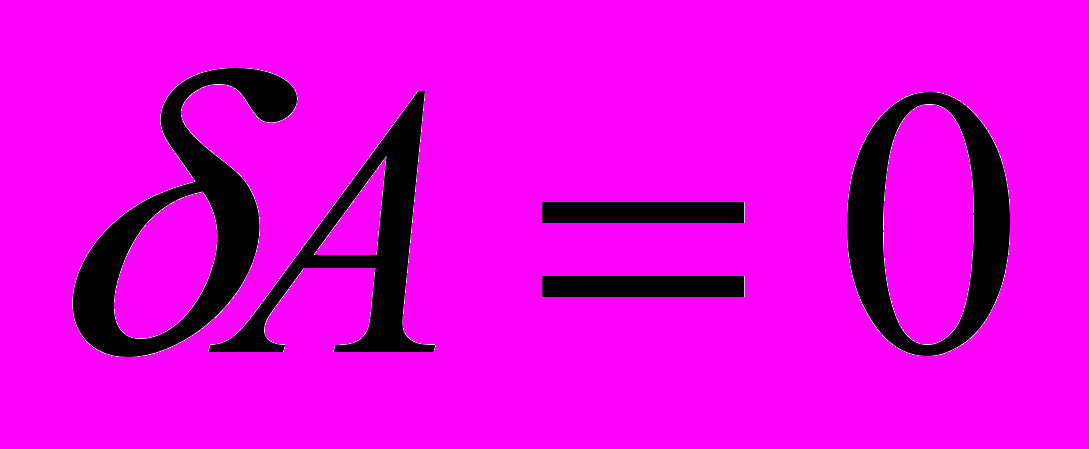 и
и 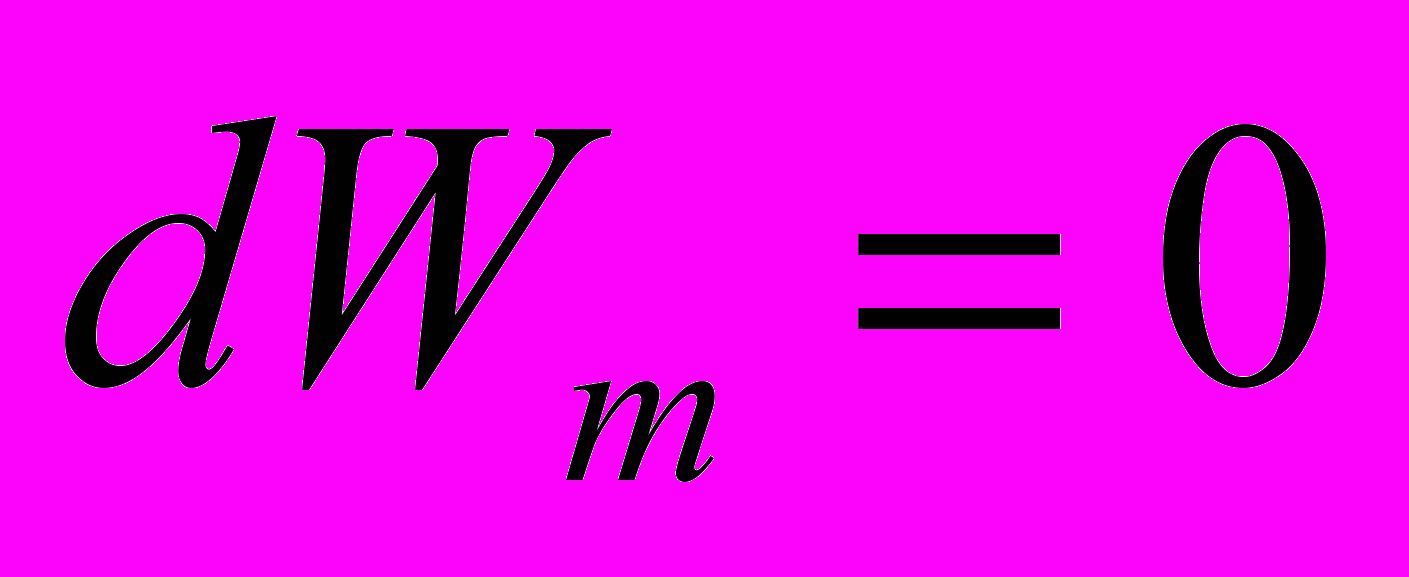 →
→ 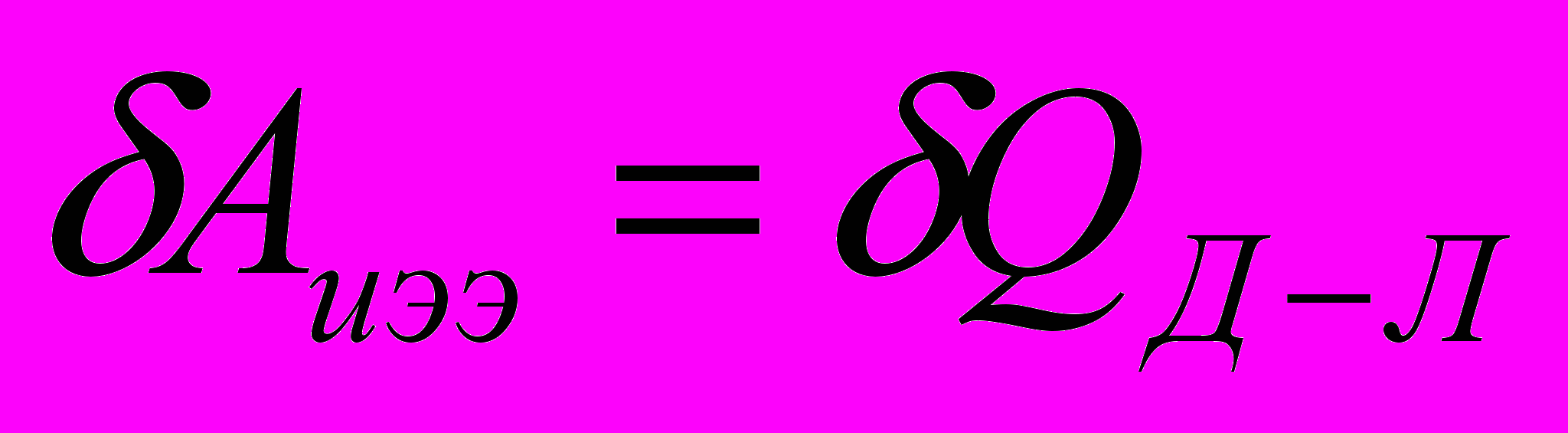
- Если ток в контуре нарастает от 0 до
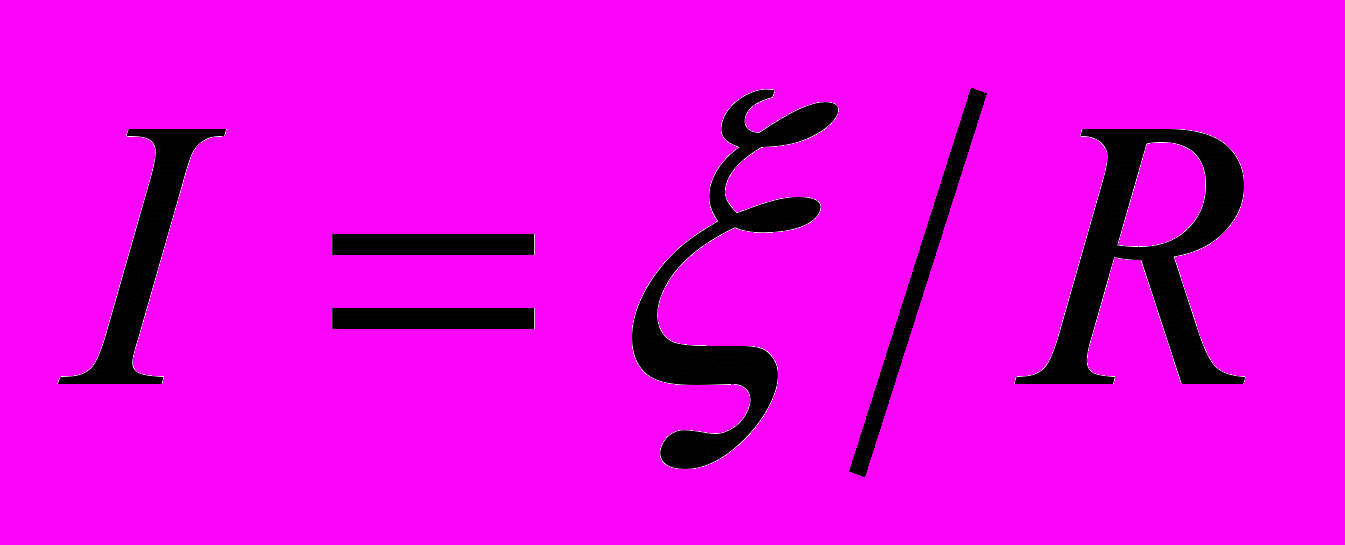 , то работа пондемоторных сил равна нулю и
, то работа пондемоторных сил равна нулю и
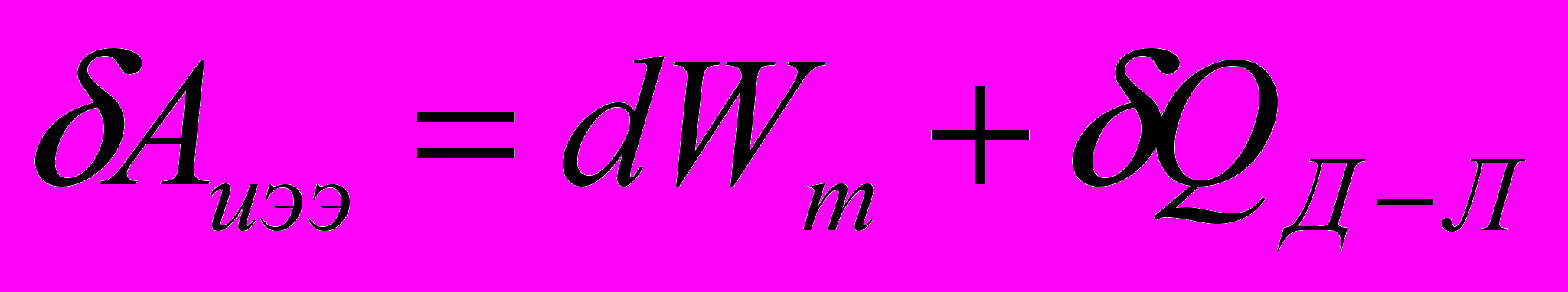 или
или