Главная
/ Ответы на экзамены / геометрия - 9 класс
| Задача по теме «Свойства прямоугольного треугольника, у которого один угол равен 30°».
Докажите, что в равностороннем треугольнике расстояние от точки пересечения двух биссектрис до стороны в два раза меньше расстояния от этой же точки до вершины. Дано: ААВС — равносторонний треугольник, DC и BF — биссектрисы, О — точка пересечения биссектрис DC и BF. Доказать: ВО = 2DO. Доказательство. Биссектриса угла равностороннего треугольника является одновременно его медианой и высотой. Отсюда следует, что в треугольнике BDO Z BDO = = 90°, a Z DBO = 30°. Следовательно, треугольник BDO — прямоугольный, и один из его углов равен 30°. Отсюда ВО = 2DO (по свойству прямоугольного треугольника, у которого один угол равен 30°). 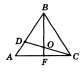 • Перейти к списку вопросов »
|
