< Предыдущая		Оглавление		Следующая >

1.6. Моделирование и символизация

В предыдущем параграфе рассматривались непосредственно техникологические модели как составная часть теории. Они определенным образом соотносятся с математическими, компьютерными и логическими моделями, о которых написаны горы книг, но, к сожалению, эта связь не всегда получает должное выражение. Довольно часто техникологические модели подменяются своими изоморфными формальными образами (интерпретациями), что недопустимо. Техниколог должен четко понимать своеобразие каждого типа моделей, используемых им. Для этого, во-первых, необходимо выяснить специфику техникологических моделей, а во-вторых, понять эффективность нетехникологических моделей. Начнем анализ с рассмотрения природы математических моделей.

А. Д. Мышки су принадлежит, пожалуй, лучшее определение математической модели: "Перейдем к общему определению. Пусть мы собираемся исследовать некоторую совокупность 5 свойств реального объекта а с помощью математики (здесь термин объект понимается в наиболее широком смысле: объектом может служить не только то, что обычно именуется этим словом, но и любая ситуация, явление, процесс и т.д.). Для этого мы выбираем (как говорят, строим) "математический объект" а' - систему уравнений, или арифметических соотношений, или геометрических фигур, или комбинацию того и другого и т.д., - исследование которого средствами математики и должно ответить на поставленные вопросы о свойствах 5. В этих условиях а' называется математической моделью объекта а относительно совокупности 5 его свойств". Однако даже такое определение вызывает вопросы. Достаточно очевидно, что с учетом разъяснения, которое дано в скобках, речь может идти не только о реальном, но и о воображаемом объекте. Весьма сомнительно также, что математическую модель необходимо сопоставлять непосредственно с 5.

Многие авторы полагают, что выработке математической модели предшествует предмодель: "Конструирование модели начинается со словесно-смыслового описания объекта или явления. <...> Данный этап можно назвать формулировкой предмодели". Нетрудно понять, что в интересующем нас контексте предмодель есть не что иное, как техникологическая модель. Однако мы полагаем, что техникологическая модель это не предмодель, а полновесный концептуальный образ, и потому мало сказать, что она является словесно-смысловым описанием объекта или явления, ибо таковым выступает и математическая модель. Итак, предмет раздора достаточно очевиден. Мы представим его в техникологическом контексте.

Одна часть авторов рассуждает в рамках концептуального каркаса: (а) технический объект -> математическая модель. Они элиминируют техникологию, при этом искажается значение как техникологии, так и математики, а упомянутая элиминация является признаком панматематизма.

Другая часть авторов использует три координаты: (б) технический объект -> предмодель -> математическая модель. По сравнению с первым вариантом появляется промежуточное звено, но его характеристика поверхностна. Тем не менее концептуальный прогресс очевиден, и нетрудно понять возможность его наращивания.

В таком случае появляется каркас: (в) технический объект -> техникологическая модель -> математическая модель. По своему потенциалу концептуальный каркас (в) превосходит своих конкурентов- каркасы (а) и (б). Но, строго говоря, и он недостаточен. Дело в том, что все три каркаса построены на иллюзии, что можна перейти к моделям непосредственно от изучаемых объектов. Мы же не устаем повторять, что научное познание реализуется как концептуальная трансдукция, одним из этапов которой выступает моделирование. Модель соотносится не только с изучаемым объектом, но и с принципами, законами, фактами и т.д. Сказанное не отменяет факта соотносительности в рамках отношения "техникологическая модель -> математическая модель". Какова природа этой соотносительности?

Математическая модель является изоморфным образом техникологической модели. Это означает, что можно установить соответствие между техникологическими и математическими концептами. Приведем простейший пример. Запишем три широко известные линейные функции:

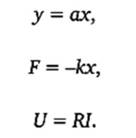
Уравнение (1) взято из математики. Уравнение (2) является записью закона Гука из теории сопротивления материалов. Уравнение (3) выражает электротехнический закон Ома. Соответствие между компонентами этих уравнений, например между у, иу буквально бросается в глаза, а пикантность ситуации состоит в том, что они относятся к различным теориям. Изоморфизм теорий указывает на их известное сходство, но в концептуальном отношении теории принципиально отличаются друг от друга. Математик компетентен в математике, физик - в физике, техниколог - в техникологии и т.д.

Стоит отметить, что вопрос о соотносительности неформальных наук и математики всегда вызывал некоторые недоумения. С легкой руки знаменитого американского физика Юджина Вигнера стали даже говорить о непостижимой эффективности математики. Действительно, вроде бы непонятно, почему обращение к математике, не входящей в состав техникологии, столь плодотворно. Но дело в том, что разделение научного труда позволило накопить в математике огромный объем знания, который в силу ее изоморфизма другим наукам, может эффективно использовать в них. Именно поэтому необходимо математическое моделирование.

Математическое моделирование в техникологии проводится в ее интересах. Термин "математическая модель" вводит в заблуждение, ибо создается впечатление о переходе в область математики. Но при математическом моделировании математика играет вспомогательную роль. Математическая модель представляет собой не что иное, как усовершенствованную техникологическую модель. Таким образом, вместо выражения "математическое моделирование" лучше использовать термин "техниколого-математическое моделирование", избегая акцента на слове "математика".

Однако математизацией техникологической модели ее улучшение не заканчивается. В современных исследованиях математическая модель, как правило, преобразуется в компьютерную модель. Решающее значение в деле компьютерного моделирования имеют создание или выбор алгоритма и написание программы обсчета математической модели. Компьютерная модель позволяет провести необходимые расчеты максимально быстро. Быстродействие компьютеров позволяет варьировать параметры математической модели, что особенно актуально при проведении мысленных экспериментов. Наконец, компьютерные модели имеют еще одно преимущество перед математическими моделями: они позволяют максимально эффективно проводить визуализацию концептуального процесса.

Компьютерную визуализацию часто связывают исключительно с выработкой визуального образа изучаемого явления, однако такая объектно-ориентированная интерпретация не соответствует истинному положению дел. В действительности создается визуальный образ не только непосредственно изучаемых явлений, но и всего процесса концептуальной трансдукции. Компьютерные модели позволяют увидеть невидимое - концепты. Похоже, что исполнилась многовековая мечта фантастов.

В связи с рассмотрением математических и компьютерных моделей необходимо упомянуть также и логическое моделирование.

Логика, как известно, стояла у истоков рождения формальных наук. Она появилась даже раньше математики. Формальная логика была создана Аристотелем в IV в. до н.э., а евклидова геометрия в качестве первой математической дисциплины, построенной в соответствии с аксиоматическим методом, появилась приблизительно век спустя.

Органическая связь логики и математики стала особенно очевидной после создания Готлобом Фреге и Бертраном Расселом математической логики. Оба они в качестве логицистов стремились свести математику к логике. Программа логицизма оказалась излишне претенциозной, но при доказательстве правильности математических теорем уже мало кто обходится без математической логики.

Органическая связь логики с информатикой и, следовательно, с теорией вычислительной техники обнаружилась очень рано. С самого начала было выявлено, что бит можно рассматривать как логическое суждение со значениями 1 (истина) и О (заблуждение), с которыми имеет дело логика Буля. Битовые операции легко описываются на языке булевской логики. В последующем связь логики с информатикой не ослабевала, а, наоборот, укреплялась. Логика оказалась особенно эффективной в деле доказательства правильности алгоритмов и программ, а также описания баз знаний и логических процедур вывода и принятия решения. В моделировании очень часто оказывается востребованным потенциал непрерывной, нечеткой и интервальной логики и родственных им формальных систем. Так, нечеткая логика имеет многочисленные применения в области моделирования функционирования технических систем в условиях неопределенности. Многие авторы считают, что логическое моделирование отнюдь не уступает по своим продуктивным возможностям математическому моделированию.

Итак, в простейшем виде техникологическое моделирование можно представить следующим образом:

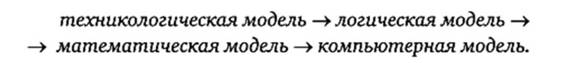
Однако с учетом сделанных выше разъяснений представленную линию модельной трансдукции имеет смысл подкорректировать:

Во всех четырех случаях речь идет о техникологических моделях. Конечно, целесообразно различать их вариации, однако всегда нужно помнить, что субстанциализация соответствующих прилагательных может привести к существенным познавательным ошибкам. Например, преобразование термина "математизированная техникологическая модель" в понятие "математическая модель" чревато искажением или даже потерей техникологической составляющей. Но техникология никогда не переходит в математику, логику или информатику.

Выше мы достаточно подробно рассмотрели вопрос о необходимости различных видов моделирования в техникологии, однако в этом деле имеются определенные ограничения. И логика, и математика в их современном виде, и компьютерные науки представлены целым спектром различных теорий, причем плюрализм теорий не уменьшается, а, наоборот, увеличивается. Поскольку все теории взаимосвязаны, то без специальных доказательств понятно, что техникология в меньшей или большей степени нуждается во всех концепциях, хотя их актуальность для техникологии различна. В любой технико-логической науке используются лишь избранные логические, математические и компьютерные теории (в том числе языки программирования). Данное обстоятельство вроде бы противоречит синтаксической природе формальных наук, в которых по определению не учитываются качественные особенности тех явлений, которые выступают объектом прагматических дисциплин. Но, как выясняется, синтаксис синтаксису - рознь. Надо полагать, именно этот феномен, приводит к избирательности в деле техникологического моделирования при использовании достижений формальных наук.

В данном параграфе рассматривается не внутренняя структура техникологии, а ее отношения с другими отраслями науки, т.е. интернаучные отношения техникологии. Если анализируются взаимоотношения техникологии с логикой, математикой и информатикой, то говорят о моделировании. Однако техникология связана также со всеми другими отраслями науки, например с физикой, химией, биологией, геологией, экономикой, политикой. Исторически так случилось, что указанным связям не присвоили какое-либо определенное имя, а между тем они этого заслуживают. Разумеется, при желании можно было бы обобщить феномен интернаучного моделирования. В таком случае пришлось бы ввести целый ряд его типов: техниколого-физическое, техниколого-химическое, техниколого-геологическое, техниколого-биологическое, техниколого-экономическое, техниколого-политологическое и т.д.

Обсуждаемую терминологическую трудность можно устранить другим путем: ввести специальный термин, который бы использовался для характеристики типов интернаучных связей. Особого внимания в этом смысле заслуживает термин "символизация", поскольку он довольно удачно выражает существо интернаучных отношений, в том числе тех из них, которые характерны для техникологии. Действительно, суть интернаучных связей состоит в том, что во взаимное соответствие ставятся концепты двух наук. Если интернаучные связи проводятся ради развития техникологии, то концепты других наук считаются символами техникологических концептов.

Пример

В энергетике, так же как и в физике, широко используется понятие энергии. Создается даже впечатление, что техническая энергия ничем не отличается от физической энергии. Но это впечатление обманчивое: понятие физической энергии органично сочетается с физическими концептами, тогда как понятие технической энергии находится в концептуальном каркасе техникологической теории. Таким образом, два понятия энергии относятся к различным наукам и потому не совпадают друг с другом. Предметом интереса техниколога является не физическая энергия, а полезная энергия, которая может эффективно использоваться человеком. Полезная энергия не входит в состав физики. Но при всем различии физической и полезной в техникологическом отношении энергии они, очевидно, не разделены непроходимым рвом. В отсутствие физической энергии нет и технической энергии, т.е. физическая энергия является условием наличия технической энергии. Демонстрируя это обстоятельство, техниколог рассматривает физическую энергию как символ, представитель технической энергии. То же самое проделывается со всеми другими понятиями, в том числе с законами и принципами, нетехникологических наук.

Любая интернаучная связь, в том числе моделирование, выступает как символизация, причем она всегда проводится в определенном направлении. В случае техниколого-физической символизации оригиналами считаются понятия техникологии, а в качестве символов выступают понятия физики.

В случае физико-техникологической символизации оригиналами выступают понятия физики. Таким образом, концептуальная символизация является той операцией, которая позволяет выразить интернаучные отношения, установить согласованность (когерентность) наук. В отсутствие когерентности наук понятийная символизация в принципе не может состояться. Следовательно, концептуальная символизация является интернаучным методом.

Выводы

1. Поскольку техникология вплетена в широкую сеть интернаучных отношений, то она имеет трансдисциплинарный характер. Соответственно, концептуальная символизация оказывается трансдисциплинарным методом.

2. Любое актуальное для техникологии моделирование производится в ее интересах.

3. При техниколого-математическом, техниколого-логическим и техниколого-компьютерном моделировании решающее значение имеет концептуальное устройство не математики, логики и информатики, а самой техникологии.

4. Интернаучным методом является концептуальная символизация, в том числе интернаучное моделирование.

< Предыдущая		Оглавление		Следующая >