< Предыдущая		Оглавление		Следующая >

7.5. Критерий ничтожных погрешностей

При измерениях, выполняемых с большой точностью, погрешность обычно округляют до двух значащих цифр.

Считается, что если погрешность округления не превышает 5%, то такой погрешностью можно пренебречь.

При определении суммарной погрешности случайных погрешностей результат выражается формулой

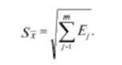
Если в этом равенстве, например, А-я погрешность такая, что

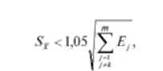
то этой погрешностью можно пренебречь, так как полученное различие при округлении теряется (число 1,05 принимается равным 1).

Возведем обе части неравенства (7.75) в квадрат и принимая во

внимание, что =o$"}-££, получим 5|-< 1,1025(5| - Ек2). Отсюда 2 0Д025 2.

следует, что частными погрешностями, меньшими < ^ |Д25

Ек <0,306 5-, можно пренебречь. Округлив последнее неравенство, получим

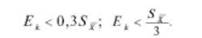
Эта формула в метрологии называется критерием ничтожных погрешностей, а сами погрешности, отвечающие условию (7.76), называются ничтожными или ничтожно малыми.

Формула (7.76) справедлива и для нескольких погрешностей, если

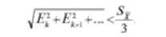
Использование критерия ничтожных погрешностей при анализе частных погрешностей косвенных измерений позволяет выделить те величины, которыми существенно влияют на погрешность результата. Повышение точности измерения этих величин позволит уменьшить суммарную погрешность.

7.6. Совокупные и совместные измерения

При совокупных и совместных измерениях искомые значения физических величин хх, х,, хт и полученные в /'-м опыте в результате прямых или косвенных измерений значения физических величин хп у/ связаны между собой уравнениями вида

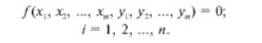
Здесь п - число опытов.

После подстановки в каждое уравнение определенных экспериментальных значений х-,, х,,хт получаем уравнение

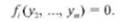
В уравнении (7.79) знак равенства имеет условный характер, гак как полученные в результате эксперимента коэффициенты содержат погрешности. Поэтому уравнения вида (7.79) называют условными.

Если уравнения (7.79) составлены из одноименных величин, то измерения называют совокупными', если физические величины, входящие в уравнения, имеют разные размерности, измерения называют совместными.

Для того чтобы рассчитать значения искомых величин, достаточно иметь т уравнений, т. е. столько, сколько имеется неизвестных. В этом случае результаты измерений и доверительные границы их погрешностей можно найти методами обработки результатов косвенных измерений. Практически для уменьшения погрешностей результатов делается значительно больше измерений, чем необходимо для определения т неизвестных (п > т).

Из-за ограниченной точности определения коэффициентов условные уравнения (7.79) одновременно не обращаются в тождества ни при каких значениях искомых величин. Так как истинные значения искомых величин определить нельзя, то задача сводится к нахождению их оценок У1У представляющих собой наилучшие приближения к истинным значениям.

Введем в каждое из уравнений (7.79) такие дополнительные слагаемые Д,, которые превращали бы их в тождества.

Значения Д, называют невязками, или остаточными погрешностями уравнений. Тогда уравнения (7.79) можно записать следующим образом:

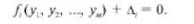
Одним из наиболее общих способов отыскания оценок истинных значений измеряемых величин является метод наименьших квадратов.

Согласно этому методу наилучшие оценки величин У{ будут получены тогда, когда сумма квадратов невязок (остаточных погрешностей) условных уравнений будет минимальна:

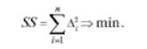
Функция нескольких переменных / достигает минимума в точке, где частные производные равны нулю.

Рассмотрим последовательность обработки экспериментальных данных совокупных или совместных измерений для случая, когда в систему уравнений входят только линейные независимые уравнения:

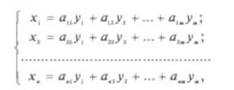
где х, - результаты наблюдений измеряемых величин (/'= I, 2,я); а{) - известные коэффициенты; у, - искомые физические величины (у = 1, 2, т).

Систему можно переписать в следующем виде:

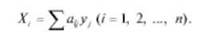
Так как результаты наблюдений х, содержат погрешность, то по аналогии с (7.80) для системы (7.83) можно написать:

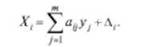
Для каждой у'-й погрешности Д, из (7.84) имеем

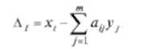
Тогда для суммы квадратов остаточных погрешностей будем иметь

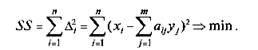
Для определения у, у удовлетворяющих условию (7.86), определим частные производные функции 55 по уп т. е.

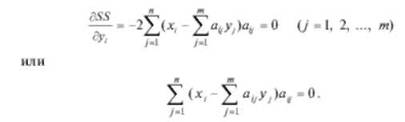
Систему (7.88) называют системой нормальных уравнений. Она является линейной относительно искомых величину. Число уравнений равно числу неизвестных величин у,.

Пользуясь обозначениями, введенными Гауссом, перепишем систему (7.88) следующим образом:

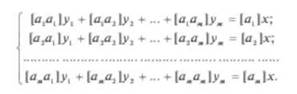
В системе (7.89) приняты следующие обозначения:

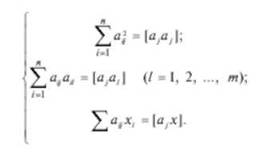
Решение системы (7.89) находят, например, с помощью определителей:

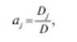
где О - определитель системы; Ц - определитель, полученный из определителя системы заменой у-го столбца столбцом свободных членов.

В настоящее время для обработки результатов эксперимента широко применяют ЭВМ. Нахождение оценок способом наименьших квадратов на ЭВМ дает возможность обработки больших массивов экспериментальных данных, в результате точность нахождения оценок может быть значительно повышена путем увеличения числа условных уравнений и, следовательно, числа наблюдений до нескольких десятков и даже сотен.

Оценку среднеквадратичного отклонения результата измерения величины у) определяют по формуле

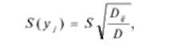
где Оц - алгебраическое дополнение определителя /); 5 - оценка среднеквадратичного отклонения уравнений:

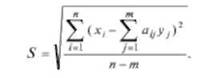
Доверительные интервалы для истинных значений всех измеряемых величин получают на основе распределения Стьюдента при числе степеней свободы, равном п - т.

< Предыдущая		Оглавление		Следующая >