Учебники
§ 1. Производство
Под «производством» в современной экономической науке принято понимать любую деятельность членов общества по использованию естественных ресурсов. В естественные Ресурсы включаются и ресурсы человека. Целью производственной деятельности является создание необходимых отдельному члену общества и обществу в целом материальных и нематериальных благ. Нередко в обиходе под «производственной деятельностью» понимается лишь создание вещественных материальных благ. Представляется, что подобная трактовка этой категории унаследована от марксистско-ленинской политической экономии, где особо выделялась деятельность в так называемом «материальном производстве», а все остальные виды деятельности считались второсортными. Вместе с тем следует учитывать и значительные различия между деятельностью работников в различных сферах производства.Одно дело - работа на машиностроительном заводе по производству персональных компьютеров, другое - их проектирование и третье — их продажа. Большей частью под «теорией производства» понимается теория процессов превращения, или трансформации, ресурсов в многообразные виды продуктов и услуг.
Поскольку производственный процесс имеет затраты (издержки) и результаты, то естественна постановка вопроса о производственной функции. Нередко производственную функцию относят к чисто техническим категориям. Это представляется неточным. Поскольку производственная функция описывает соотношение между издержками и результатами, она неизбежно как бы соприкасается с эффективностью самой функции и ее аргументов. Очевидно, правильнее говорить о производственной функции как категории промежуточной. Более эффективным признается тот технологический способ производства, который обеспечивает большее количество продукции при заданных ресурсах или, наоборот, требует меньшего объема ресурсов для получения заданного объема продукта. Нетрудно заметить, что эффективность различных технологических способов производства в огромной степени определяется уровнем цен на ресурсы и продукты. По-видимому, это еще один аргумент в пользу того, чтобы считать производственную функцию категорией, близкой к экономической. Это имеет существенное значение для общества в целом и для каждого экономического агента.
Запись производственной функции не представляет особых трудностей для студентов подавляющего большинства вузов, ибо они хорошо знакомы с математикой.
Итак, продукцию следует рассматривать как поток, т.е. в определенном измерении в единицу времени. Так как для создания каждого вида продукции есть множество хронологических способов производства, правомерно утверждение, что в системе координат факторов производства будет множество точек, отображающих соответствующее количество факторов, необходимых для данного технологического способа производства, т.е. обеспечивающих заданный выпуск. Обычно эти точки составляют линии, имеющие изогнутую форму и называются «изоквантами». Разные сочетания факторов производства имеют различные объемы выпуска. Поэтому на графике производственной функции мы наблюдаем семейство изоквант. Разрыв между изоквантами в системе координат характеризует различия в объемах выпуска продукции.
Изменение соотношения между используемыми факторами производства отражается движением по каждой изокванте. Один фактор замещает другой при создании определенного объема продукта. Это принято называть «замещением», а наклон изокванты - «предельной нормой замещения». Понятно, что изокванты могут иметь самые разнообразные формы: прямая линия (совершенная замещаемость; постоянная норма замещаемости); два отрезка, соединенные вместе под прямым углом; несколько отрезков, соединенных под тупыми углами, и т.п.
На практике, в конкурентной борьбе за максимизацию прибыли одним из важнейших средств выступает увеличение объема выпуска продукции. Этого можно добиться двумя основными путями: 1) интенсифицировать использование наличных производственных мощностей; 2) осуществить инвестиции, т.е. расширить мощности и привлечь новых работников. В связи с этим время производства можно классифицировать как мгновенный, средний (короткий) и длительный периоды, о которых шла речь при рассмотрении теории спроса и предложения. Вспомним, что с расширением производственных мощностей возникает эффект масштаба.
Возможны следующие варианты эффекта масштаба (рис. 7.1). Во-первых, при увеличении факторов в несколько раз в таком же отношении возрастает объем выпуска. Это будет постоянная отдача от масштаба. Эффект масштаба может быть возрастающим, если объем продукции возрастает. Если 1 = 1, то функцию принято называть «однородной» и п будет показателем однородности. Если это условие не выполняется, то функция неоднородна. При п = 1 эффект масштаба постоянен и функция называется «линейно-однородной». Таким образом, при п < 1 имеет место убывающий эффект масштаба, при п > 1 отдача от масштаба возрастает. Постоянная отдача от масштаба обычно имеет место в технологически простых производствах. Отрицательный эффект масштаба - по преимуществу в сложных производствах, например с наукоемкой технологией.
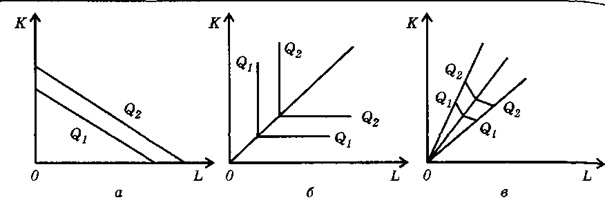
Высказанные выше относительно простые положения дают возможность в случае необходимости рассмотреть на семинарских занятиях варианты эффекта масштаба применительно к мгновенным, средним и длительным периодам.
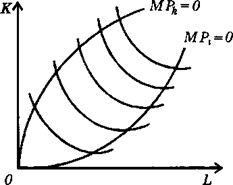
Обратимся еще к одному существенному моменту. До сих пор, когда речь шла об изоквантах, мы не ставили вопроса об их границах. Это означало, что теоретически у изоквант не существует границ. Безусловно, это так. Но предпринимателя интересует не вся длина изокванты, а лишь тот ее участок, на котором предельные продукты каждого из ресурсов остаются положительными, хотя и убывают. Все точки на изоквантах, отражающие нулевые предельные продукты, образуют границы эффективной области изоквант (рис. 7.2).
< Назад Вперед >
Содержание
