Авторефераты по темам  >>  Разные специальности - [часть 1]  [часть 2]

ОПРЕДЕЛЕНИЕ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК НЕЛИНЕЙНО-УПРУГИХ ВОЛН С ЦЕЛЬЮ ДИАГНОСТИКИ МАТЕРИАЛОВ И ЭЛЕМЕНТОВ КОНСТРУКЦИЙ

Автореферат кандидатской диссертации

 

На правах рукописи

ДЕНИСОВА Татьяна Сергеевна

ОПРЕДЕЛЕНИЕ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК НЕЛИНЕЙНО-УПРУГИХ ВОЛН С ЦЕЛЬЮ ДИАГНОСТИКИ МАТЕРИАЛОВ И ЭЛЕМЕНТОВ КОНСТРУКЦИЙ

 

01.02.06 - Динамика, прочность машин, приборов и аппаратуры

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата технических анаук

 

 

Нижний Новгород - 2012
Работа выполнена в Нижегородском филиале Федерального государственного бюджетного учреждения науки Института машиноведения им. А.А. Благонравова Российской академии наук

Научный руководитель:а доктор физико-математических наук, профессор

аЕрофеев Владимир Иванович

Официальные оппоненты: доктор физико-математических наук, профессор

аВолков Иван Андреевич

кандидат технических наук, доцент

аХлыбов Александр Анатольевич

Ведущая организация: АНО НаучноЦисследовательский центр контроля и диагностики технических система (г. Нижний Новгород).аа

Защита состоится 23 мая а2012 г. в 16-00 на заседании диссертационного совета Д 212.165.08 в Нижегородском государственном техническом университете им. Р.Е. Алексеева по адресу: 603950, Нижний Новгород, ул. Минина, 24, ауд. 1258.

C диссертацией можно ознакомиться в библиотеке Нижегородского государственного технического университета им. Р.Е. Алексеева.

Ваш отзыв на автореферат, заверенный печатью организации, просим направлять по адресу: 603950, Нижний Новгород, ул. Минина, 24, НГТУ, ученому секретарю диссертационного совета Д 212.165.08.

Автореферат разосланаа л_____________2012г.

Учёный секретарь диссертационного совета, доктор технических наук

Е.М. Грамузов

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность темы. Такие свойства упругих волн, как способность распространяться с конечной скоростью, переносить энергию без переноса вещества, давно и эффективно используются в неразрушающем контроле материалов и конструкций. Многие методы определения напряженно-деформированного состояния, структуры и свойств материалов (например, метод акустоупругости) основаны на измерении скорости волнового пакета - групповой скорости. Для линейных волн групповую скорость справедливо отождествляют со скоростью переноса энергии. Соотношения, связывающие групповую скорость и скорость переноса энергии для нелинейных систем, на сегодняшний день, практически не исследованы, и это представляется актуальной задачей.

В ряде монографий и обзоров (см., например, Бабешко В.А., Глушков Е.В., Зинченко Ж.Ф. Динамика неоднородных линейно-упругих сред. М.: Наука, 1989. 344 с.) отмечается, что количество переносимой волнами энергии является, наряду с амплитудой и фазой, важной характеристикой волнового поля. При этом подчеркивается, что энергетический анализ не сводится к амплитудному, а требует разработки специального подхода.

При изучении распространения волн в таких широко распространенных машиностроительных конструкциях, как среды с препятствиями, решетки и твердые волноводы, следует уделять особое внимание, как дисперсионным характеристикам, так и анализу потоков колебательной энергии. В задачах отражения наиболее важным является вопрос о потоках энергии в падающих и отраженных волнах. Отражение волн от препятствий или неоднородностей лежит в основе теории виброизоляции конструкций.

Дж. Гордоном предложен, а В.П. Малковым развит подход, рассматривающий механические системы и их элементы соответственно как глобальные и локальные резервуары энергии. Этими авторами вводятся понятия глобальных и локальных относительных энергетических критериев; выполняется энергетический анализ типовых экспериментальных диаграмм деформирования стандартных образцов материалов. Во многих публикациях отмечается перспективность такого энергетического подхода для расчета динамической прочности элементов конструкций.

Основные результаты диссертации были получены в рамках Программы фундаментальных научных исследований государственных академий наук на 2008Ц2012 г.г. в ходе выполнения работ по темам:

по темам:

- Разработка методов повышения ресурса и надежности сложных технических систем путем применения наноструктурных материалов и градиентных защитных покрытий, диагностики на ранних стадиях повреждения и мониторинга состояния материалов и конструкций в процессе эксплуатации (№ Гос.рег. 01200957043; научный руководитель: академик РАН Митенков Ф.М.);

- Разработка моделей и методов расчета нелинейных волновых процессов, хаотической синхронизации и формирования кластерных структур в машинах, создание высокоэффективных адаптивных систем виброзащиты (№ Гос.рег. 01200957044; научный руководитель: профессор Ерофеев В.И.)

и при поддержке:

- Федеральной целевой программы Научные и научно-педагогические кадры инновационной России (2009 - 2013 г.г.);

- Гранта Российского фонда фундаментальных исследований Нелинейные упругие волны в структурированных и поврежденных материалах и элементах конструкций. Теория. Эксперимент. Приложения в технической диагностике (РФФИ № 09-08-00827; руководитель: профессор Ерофеев В.И.).

Цель работы состоит в определении для нелинейно-упругих волн дисперсионных и аэнергетических характеристик, необходимых при разработке методик неразрушающего контроля материалов и элементов конструкций.

Научная новизна работы заключается в определении:

- величины отношения скорости переноса энергии одномерных нелинейных упругих волн к групповой скорости;

- зависимостей, связывающих асреднюю плотность потока энергии и среднюю плотность изгибных волн, распространяющихся в балке, с модулем Юнга, с площадью и формой поперечного сечения балки.

Практическая значимость. Упругие волны представляют собой высокоэффективный инструмент исследования напряженно-деформированного состояния, структуры и свойств материалов. Дисперсионные и энергетические характеристики изгибных волн могут найти применение при расчете на прочность, устойчивость и определение виброактивности стержневых систем различного назначения, подверженных динамическому воздействию, в частности, несущих движущуюся нагрузку. Соотношения, связывающие групповую скорость и скорость переноса энергии для нелинейных систем, могут найти применение в технической диагностике. Знание истинной скорости переноса энергии упругими волнами весьма важно, поскольку многие методы диагностики материалов и конструкций (например, метод акустоупругости) основаны на измерении скорости волнового пакета.

Результаты диссертационной работы использовались в ООО Научно-исследовательская лаборатория испытания материалов при разработке методики ультразвукового контроля высоконагруженных элементов машиностроительных конструкций (Имеется акт внедрения).

Методы исследования. При проведении исследований использованы аналитические методы механики деформируемого твердого тела, теории колебаний и волн.

Достоверность полученных результатов и выводов подтверждается их согласованностью с общими положениями механики деформируемого твердого тела, теории колебаний и волн, а также согласованностью результатов расчетов с известными экспериментальными данными.

На защиту выносятся:

- Результаты исследования дисперсионных и энергетических характеристик поперечных волн, распространяющихся в струне, лежащей на нелинейно-упругом основании и нелинейно-упругой балке.

- Результаты исследования дисперсионных и энергетических характеристик нелинейных сдвиговых волн, распространяющихся в градиентно-упругих материалах.

Апробация работы.

Результаты работы докладывались и обсуждались: наа Второй Всероссийской научной конференции по волновой динамике машин и конструкций (Нижний Новгород, 28-31 октября 2007 года); на XIII Нижегородской сессии молодых ученых (Технические науки) (Нижний Новгород - Татинец, 17-21 февраля 2008 года). аВ полном объеме диссертация обсуждалась на семинарах отдела волновой динамики и виброзащиты машин НФ ИМАШ РАН (2010, 2011 г.г.).

Публикации. По материалам диссертации опубликовано 8 работ, 3 из которых [1- 3] - статьи в рецензируемых научных журналах.

Структура и объем диссертации. Работа состоит из введения, трех глав и заключения. Общий объем составляет 110 страниц, включая 15 рисунков, 2 таблицы, 15 страниц библиографии, содержащей 134 наименования.

СОДЕРЖАНИЕ РАБОТЫ

Во введении дана общая характеристика работы, сформулирована ее цель, основные положения, выносимые на защиту, определены научная новизна и практическая значимость диссертации.

В первой главе рассмотрены особенности распространения поперечных волн в струне на линейно - и нелинейно-упругом основаниях. Выведено уравнение переноса энергии. Исследовано изменение скорости переноса энергии изгибных волн, распространяющихся в линейной и нелинейной балке модели Бернулли-Эйлера.

Уравнение поперечных колебаний струны, лежащей на упругом основании: 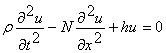, где u Ч смещение точки в пространстве, ? - линейная плотность, h - коэффициент, характеризующий жесткость основания, N - натяжение.

Частота и волновое число k связаны соотношением , агде а- скорость распространения возмущений, а через аобозначена критическая частота, при превышении которой колебания струны носят волновой характер.

Поперечные волны в струне, лежащей на упругом основании, обладают нормальной дисперсией. Найдены фазовая скорость, групповая скорость. Величина аапредставляет собой максимально возможное значение скорости поперечных волн и достигается при бесконечном увеличении частоты.

Выведено уравнение переноса энергии. В общем виде оно выглядит так: а- уравнение Умова-Пойнтинга, гдеа W- плотность энергии, S - плотность потока энергии. Величина отношения плотности потока волновой энергии к плотности энергии определяет величину скорости переноса энергии , где а- скорость переноса энергии. Найдены средние величины: аи . Скорость переноса энергии для данной системы равна отношению этих средних: 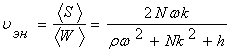. Доказано, что . Можно утверждать, что в линейных задачах энергия переносится со скоростью движения волнового пакета Ч групповой скоростью волн.

Уравнение поперечных колебаний струны, лежащей на нелинейно-упругом основании отличается от линейного тем, что в нем имеется несколько коэффициентов, характеризующих жесткость основания: . Нелинейное дисперсионное уравнение выглядит так: . В нелинейной задаче частота ? зависит не только от волнового числа k, но и от амплитуды колебаний А. Колебания струны будут иметь волновой характер при условии, когда частота колебаний превышает критическое значение . Групповая скорость при поперечных колебаниях струны будет равна 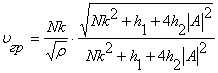. Скорость переноса энергииопределяем как отношение средних плотности и потока энергии: .

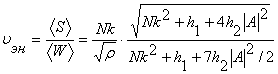Таким образом, скорость переноса энергии не равна групповой скорости. Для исследования энергетических характеристик поперечных колебаний струны, лежащей на нелинейно-упругом основании сравним групповую и скорость переноса энергии волн.а .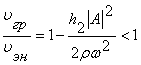

Скорость переноса энергии больше групповой скорости. При увеличении частоты отношение увеличивается, его предельное значение при ?> ? и фиксированной амплитуде равно единице, т.е. при большой частоте скорости близки и стремятся к значению . При уменьшении частоты отношение скоростей уменьшается. При а(при меньших частотах колебания не будут иметь волнового характера) отношение скоростей стремится к наименьшему значению 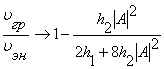. Проанализировав данное отношение, видим, что при увеличении амплитуды колебаний это выражение стремится к числу 7/8, которое характеризует максимальную разницу между скоростями. При малой амплитуде колебаний отношение скоростей близко к единице. Можно заметить, что в нелинейной системе присутствует нормальная дисперсия , т.е. групповая скорость волны меньше, чем ее фазовая скорость.

Уравнение изгибных колебаний балки (модель БернуллиЦЭйлера) имеет вид: 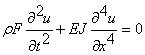, где u - поперечное перемещение частиц срединной линии балки, J - осевой момент инерции прямоугольного поперечного сечения, а- плотность, F - площадь поперечного сечения, Е - модуль Юнга.

Получено дисперсионное уравнение , найдены фазовая и групповая скорости. Изгибные волны распространяются вдоль балки с дисперсией. Форма любого негармонического возмущения будет искажаться по мере его распространения. Дисперсия системы имеет аномальный характер. Групповая скорость волны при любой частоте будет в два раза превышать фазовую.

Выведено уравнение переноса энергии изгибных волн. Найдена скорость переноса энергии для данной системы .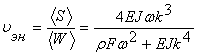

Получено, что в линейном случае скорость переноса энергии и групповая скорость волн равны .

Рассмотрим другую систему - нелинейную балку бесконечной длинны. Уравнение динамики геометрически нелинейной балки имеет вид: , где а - коэффициент нелинейности. Геометрическая нелинейность - это нелинейность между перемещениями и деформациями. Дисперсионное уравнение для этой системы выглядит следующим образом: . Для данной системы частота ? зависит как и от волнового числа k, так и от амплитуды колебаний А. Групповая скорость при данных колебаниях будет равна 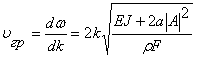. В этой системе имеет место аномальная дисперсия. Найдена скорость переноса энергии: 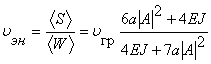. Скорость переноса энергии не равна групповой скорости. Сравним скорости, найдем их отношение. .

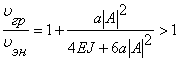Анализ показал, что скорость переноса энергии меньше групповой скорости, причем их отношение зависит от амплитуды колебаний и не зависит от волнового числа и частоты. Проанализируем пределы отношения. Предельное значение отношения при амплитуде колебаний, стремящейся к нулю, близко к единице, значит волны будут линейными. При бесконечном увеличении амплитуды отношение стремится к максимальному значению, равному 7/6, т.е. скорость переноса энергии составляет 0.86 от групповой скорости.

Во второй главе изучены некоторые свойства средней плотности энергии и плотности потока энергии линейных изгибных волн, распространяющихся в балке модели БернуллиЦЭйлера в зависимости от изменения различных параметров уравнения переноса энергии.

В предыдущей главе были получены выражения средней плотности и потока энергии линейных изгибных волн, распространяющихся в балке БернуллиЦЭйлера.

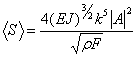, (1)

, аа (2)

где J - осевой момент инерции поперечного сечения, а- плотность, F - площадь поперечного сечения, Е - модуль Юнга, k - волновое число, А - амплитуда колебаний.

Анализ выражений (1) и (2) показал следующее поведение средней плотности и потока энергии изгибных волн.

Чем больше длина волны ?, тем поток и плотность энергии будут меньше.

Рассмотрена зависимость плотности энергии (2) и плотности потока энергии (1) от формы поперечного сечения балки одинаковой площади. Выберем круглое, прямоугольное и треугольное сечение (рис. 1).

Рис. 1. Формы поперечного сечения балки

Площади фигур соответственно равны: а- площадь круга, а- площадь прямоугольника, а- площадь треугольника. Осевые моменты инерции фигур равны: , , .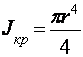

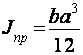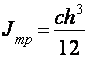Проведен сравнительный анализ. Получены следующие результаты. При прочих равных условиях для поперечных сечений балки одинаковой площади, но разной формы справедливы следующие неравенства , < < , здесь S - средняя плотность потока энергии, < < , здесь W - средняя плотность энергии.

Итак, осевой момент инерции, поток и плотность энергии для круглого сечения балки больше, чем для треугольного и прямоугольного.

Одним из параметров определяющих упругость материала является модуль Юнга. Рассмотрено несколько материалов. Составлена таблица материалов по возрастанию модуля Юнга материала (табл. 1) .

Т а б л и ц а 1

Значения характеристик материалов

Материал	Модуль Юнга, Е, ГПа	Плотность, ?*103,кг/м3	<W>*1012	<S> ~ (E3/2/?1/2) *1012
Стекло органическое	3.00	1.19	3.00	4.78
Оргстекло	4.13	1.18	4.13	7.73
Текстолит	10.00	1.35	10.00	27.73
Стекловолокнит	22.00	1.80	22.00	79.14
Стеклопластик	35.00	1.70	35.00	161.20
Алюминий	70.61	2.69	70.61	361.83
Золото	80.50	19.32	80.50	156.73
Агат	98.00	2.65	98.00	613.58
Железо	200.00	7.87	200.00	970.41
Сталь	206.33	7.80	206.33	1061.16

Графическое представление зависимости асредней плотности энергии <W> от модуля упругости материала Е аизображено на рисунке 2.

Рис. 2. Зависимость плотности энергии от модуля упругости материала

Итак, получено, что с увеличением модуля упругости материала плотность энергии так же увеличивается. При прочих равных условиях, чем больше площадь поперечного сечения, тем плотность потока энергии меньше.

По значениям табл. 1 составлен график зависимости средней плотности потока энергии <S> от модуля упругости материала Е (рис. 3).

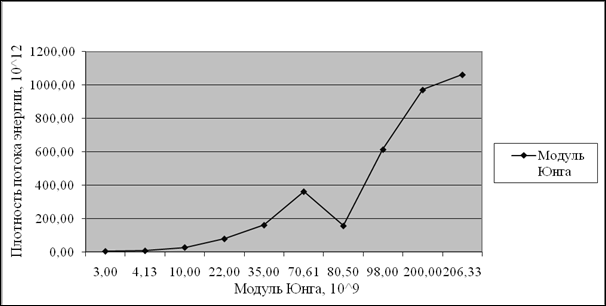
Рис. 3. Зависимость плотности потока энергии от модуля упругости материала

Видно, что плотность потока энергии увеличивается с ростом модуля Юнга материала, исключение составляет золото.

Третья глава посвящена анализу соотношений, связывающих групповую скорость и скорость переноса энергии сдвиговой волны, распространяющейся в нелинейном градиентно-упругом материале.

В первом параграфе главы приводится обзор экспериментальных исследований дисперсии упругих волн в конструкционных материалах. Показано, что в ультразвуковом диапазоне у одних материалов (металлы и их сплавы) наблюдается уменьшение фазовых скоростей упругих волн с ростом частоты (отрицательная дисперсия). Для других материалов (некоторые зернистые и армированные композиты) наблюдается увеличение фазовых скоростей упругих волн с ростом частоты (положительная дисперсия).

Плоские сдвиговые волны, распространяющиеся в градиентно-упругой среде в направлении оси , описываются уравнением

аа (3)

Здесь u, x, t - безразмерные перемещение, координата и время, , а - малые параметры, характеризующие дисперсию и нелинейность среды, соответственно.

На основе проведенного анализа экспериментальных данных доказано, что модель градиентно-упругой среды позволяет описывать как отрицательную, так и положительную дисперсии.

Выявлено, что входящая в предложенную модель дополнительная константа хорошо скоррелирована со средним диаметром зерна в материале.

Показано, что наблюдается уменьшение скорости звука в материалах (алюминиевый сплав Д 16, бронза БРОФ) с увеличением среднего диаметра зерна.

Проанализируем, как соотносятся между собой скорость переноса энергии и групповая скорость сдвиговой волны. Для этого зададим их отношение:

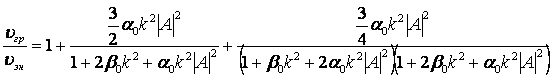а (4)

Известно, что для большинства твердых тел параметр нелинейности отрицателен, следовательно, отношение скоростей будет зависеть от величины и знака параметра дисперсии .

К материалам с отрицательным параметром дисперсии относится большинство металлов и их сплавов, к материалам с положительным параметром дисперсии - многие армированные композиты.

Для обоих случаев зависимости (4) имеют гиперболический характер. Отношение скоростей может принимать любые значения. При бесконечном убывании или возрастании значений параметра дисперсии отношение скоростей близко к единице, т.е. скорость переноса энергии близка к групповой скорости, а та, в свою очередь, стремится к скорости распространения линейной сдвиговой волны в материале (). График всегда проходит через точку , то есть во всех случаях при значении параметра дисперсии агрупповая скорость волн в 2,5 раза больше скорости переноса энергии, т.е. а. При переходе вертикальной асимптоты через начало координат график из убывающего становится возрастающим. В случае, когда групповая скорость волн меньше скорости переноса энергии , есть области значений, где скорости становятся противоположными по направлению.

В заключении приводятся основные результаты и выводы по работе.

 

ОСНОВНЫЕ РЕЗУЛЬТАТЫ ДИССЕРТАЦИИ

1. Определены скорости переноса энергии поперечными волнами в следующих одноменых упругих системах: струна, лежащая на нелинейно-упругом основании,а нелинейно-упругая балка модели Бернулли-Эйлера. Проанализировано отношение групповой скорости волн к скорости переноса энергии в зависимости от амплитуды волны и ее частоты. Показано, что в струне, лежащей на нелинейно-упругом основании, скорость переноса энергии больше групповой скорости поперечных волн. Отношение этих скоростей азависит от амплитуды волны и ее частоты. В нелинейно-упругой балке скорость переноса энергии меньше групповой скорости изгибных волн, отношение этих скоростей зависит ота амплитуды волны и не зависит от ее частоты.
2. Определены зависимости средних значений плотности энергии и плотности потока энергии, переносимой изгибными волнами в балке, от площади поперечного сечения балки, формы сечения, модуля Юнга материала. Показано, что плотность потока энергии увеличивается с ростом модуля Юнга и уменьшается с увеличением площади поперечного сечения балки. При равенстве площадей поперечного сечения плотность потока энергии для балки кругового поперечного сечения больше, чем для балок треугольного и прямоугольного поперечных сечений. Все перечисленные закономерности справедливы и для плотности энергии.
3. На основе анализа экспериментальных данных показано, что:

-а в ультразвуковом диапазоне у одних материалов (металлы и их сплавы) наблюдается уменьшение фазовых скоростей упругих волн с ростом частоты (отрицательная дисперсия). Для других материалов (некоторые зернистые и армированные композиты) наблюдается увеличение фазовых скоростей упругих волн с ростом частоты (положительная дисперсия);

- математическая модель градиентно-упругой среды позволяет описывать как отрицательную, так и положительную дисперсии;

-а входящая в предложенную модель дополнительная константа хорошо скоррелирована со средним диаметром зерна в материале;

- наблюдается уменьшение скорости звука в материалах (алюминиевый сплав Д 16, бронза БРОФ) с увеличением среднего диаметра зерна.

1. Получены и проанализированы соотношения, связывающие групповую скорость и скорость переноса энергии сдвиговой волны, распространяющейся в нелинейном градиентно-упругом материале. Показано, что отношение скоростей зависит от дисперсионного параметра и имеет гиперболический характер. При бесконечном убывании или возрастании значений дисперсионного параметра отношение скоростей близко к единице, т.е. скорость переноса энергии близка к групповой скорости, а та, в свою очередь, стремится к скорости распространения линейной сдвиговой волны в материале.

СПИСОК ОПУБЛИКОВАННЫХ РАБОТ АВТОРА ПО ТЕМЕ ДИССЕРТАЦИИ

I. Публикации в рецензируемых журналах:

1. Ерофеев В.И., Денисова Т.С., Миклашевич И.А. О скорости переноса энергии сдвиговыми волнами, распространяющимися в градиентно-упругом материале // Механика композиционных материалов и конструкций. 2011. Т.17. № 4. С. 455-461.

1. Денисова Т.С., Ерофеев В.И., Смирнов П.А. О скорости переноса энергии упругими волнами, распространяющимися в струне и балке // Вестник Нижегородского университета им. Н.И. Лобачевского. - 2011. - № 6. С. 200-202.
2. аГерасимов С.И., Денисова Т.С., Ерофеев В.И. Скорость переноса энергии сдвиговой волны, распространяющейся в градиентно-упругом материале // Вопросы атомной науки и техники. Сер.: Теоретическая и прикладная физика. 2011. № 3. С. 37-41.

II. Публикации в других изданиях:

• Денисова Т.С. Анализ энергетических характеристик упругих волн, распространяющихся в струне и балке // Вторая Всероссийская научная конференция по волновой динамике машин и конструкций. Тезисы докладов. Нижний Новгород. - 2007. - С. 31.
• Денисова Т.С. Анализ энергетических характеристик упругих волн, распространяющиеся в струне и балке // Прикладная механика и технологии машиностроения. Сборник научных трудов. Нижний Новгород: Изд-во Интелсервис. - 2007. - № 1(10). - С. 164-172.
• Денисова Т.С. Случайные колебания струны при действии возмущающей нагрузки // Прикладная механика и технологии машиностроения. Сборник научных трудов. Нижний Новгород: Изд-во Интелсервис. - 2007. - № 2(11). - С. 46-55.
• Денисова Т.С. Энергетические характеристики упругих волн, распространяющиеся в элементах конструкций // Нижегородская сессия молодых ученых. Технические науки. Материалы докладов. Нижний Новгород. - 2008. - С. 76.
• Денисова Т.С Энергетические характеристики нелинейных плоских сдвиговых волн в твердых телах с моментными напряжениями // Прикладная механика и технологии машиностроения. Сборник научных трудов. Нижний Новгород: Изд-во Интелсервис. - 2009. - №2(15). - С. 67-87.
     Авторефераты по темам  >>  Разные специальности - [часть 1]  [часть 2]