 Авторефераты по темам >>
Разные специальности - [часть 1] [часть 2]
Авторефераты по темам >>
Разные специальности - [часть 1] [часть 2]
Устойчивость и несущая способность скошенных композитных панелей
Автореферат кандидатской диссертации
аНа правах рукописи
ГАЙДАРЖИ ЮРИЙ ВАСИЛЬЕВИЧ
УСТОЙЧИВОСТЬ И НЕСУЩАЯ СПОСОБНОСТЬ СКОШЕННЫХ КОМПОЗИТНЫХ ПАНЕЛЕЙ
Специальность 01.02.06 ЦДинамика, прочность машин, приборов и аппаратуры
Автореферат диссертации ана соискание ученой степени кандидата
технических наук
Москва - 2012
Работа выполнена в МАТИ - Российском государственном технологическом университете им. К.Э.Циолковского на кафедре Прикладная и вычислительная механика.
Научный руководитель:а д.т.н, профессор, Азиков Николай Сергеевич.
Официальные оппоненты: аа
Сухинин Сигизмунд Николаевич, д.т.н., профессор, ФГУП ЦНИИМАШ, начальник лаборатории
Лысухин Владимир Иванович, к.т.н, доцент, ОАО Туполев, начальник бригады САПР
Ведущая организация: Центральный Научно-Исследовательский Институт Специального Машиностроения.
Защита состоится ал24 амаяа 2012 г. в а15 ачасов
на заседании диссертационного совета Д212.110.07 в МАТИ - Российском государственном технологическом университете им. К.Э.Циолковского по адресу: 119111, г. Москва, ул. Оршанская, д.3.
С диссертацией можно ознакомиться в библиотеке
МАТИ-Российском государственном технологическом университете им. К.Э.Циолковского.
Автореферат разослан л12 апреля 2012 г.
Ученый секретарь
диссертационного советаа Чуфистов Владимир Алексеевич
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
аа Актуальность темы. аМеталлические подкрепленные и неподкрепленные панели в настоящее время широко распространены в самолето- и судостроении. Их применяют как в силовых элементах конструкции, так и в несиловыха (перегородки, в элементах декора) и.т.д. При этом панели могут иметь различные в плане геометрическиеформы: ромбовидные, треугольные, трапециевидные и т.д. аСуществует достаточно много публикаций, связанных с прочностным анализом традиционных панелей прямоугольной формы и практически отсутствуют данные по оценке несущей способности апанелейкосоугольной формы. Кроме традиционных изотропных материалов в аэрокосмической технике получили применение высокопрочные и высокомодульные композиционные материалы на основе углеродных, борных и других типов волокон, полимерных и керамических матриц. Имеющийся ограниченный опыт внедрения композитных панелей в конструкции самолетов показал, что их прочность, устойчивость и несущую способностьа при сжатии и сдвиге трудно прогнозировать существующими расчетными методами, а типичные для композитов локальные разрушения в значительной степени ограничивают выигрыш в эксплуатационных характеристиках по сравнению с металлами. Поэтому композиты в настоящее время используются, в основном, в тонкостенных элементах, работающих до потери устойчивости.
Широкое применение композиционных материалов в скошенных тонкостенных элементах авиационной и космической техники связано с актуальной проблемой разработки прикладного метода расчета на устойчивость и несущую способность панелей с различными вариантами подкрепления контура при сжатии, сдвиге и комбинированном нагружении, а также поиском структур армирования, реализующих высокие удельные жесткостные и прочностные характеристики современных композиционных материалов.
аа Целью работы является разработка прикладного метода определения устойчивости и несущей способности скошенных слоистых композитных панелей с различными граничными условиями на контуре при сжатии, сдвиге и комбинированном нагружении.
Для достижения поставленной цели потребовалось решить следующие задачи:
- разработать прикладной метод определения устойчивости и несущей способности скошенных слоистых композитных панелей при сжатии, сдвиге и комбинированном нагружении с произвольными граничными условиями по контуру;
- исследовать влияние углов скоса, схем армирования и граничных условий на критические усилия устойчивости композитной панели при действии сжимающих и касательных усилий;
- из условия максимума критических усилий определить рациональные структуры армирования скошенных слоистых панелей;
- оценить найденные структуры армирования по несущей способности панели после потери устойчивости.
аа Научная новизна работы определяется:
- аасоотношениями механики скошенных систем;
- методом решения обобщенной задачи на собственные значения для скошенных слоистых систем;
- разработанным методом решения геометрически нелинейных задач в конечных разностях без использования фиктивных точек;
- найденными закономерностями между геометрией контура панели, структурой армирования слоев, граничными условиями и критическими и разрушающими усилиями для скошенных слоистых композитных панелей.
аа Практическая значимость работы определяется
- предложенным энергетическим методом решения задачи устойчивости скошенной панели, опирающимся на модифицированные балочные функцииа и позволяющим находить критические усилия сжатия и сдвига композитных панелей;
- способом решения задачи о закритическом деформировании слоистых панелей с произвольными граничными условиями в конечных разностях;а
- апроведенными исследованиями влияния углов скоса, структуры армирования композитных слоев и видов граничных условий ана устойчивость и закритическое деформирование панелей при изолированном нагружении сжимающими и касательными усилиями и при одновременном действии сжатия и сдвига;
- найденными из условия максимума критических усилий сжатия и сдвига рациональными структурами армирования;
- оценкой несущей способности композитных панелей, находящихся в условиях закритического деформирования при сжатии, сдвиге или комбинированном нагружении.
аа Достоверность результатов диссертации обеспечивается использованием общепринятых соотношений строительной механики тонкостенных конструкций и механики композитов, известными численными методами и подтверждается сопоставлением теоретических результатов с опубликованными данными.
аа Апробация работы. Основные результаты исследований, изложенные в диссертации, докладывались на :
-XXXVII Международной молодежнойа научной конференции Гагаринские чтения, Москва,5-8 апреля 2011г.
аа Публикации. Основное содержание и результаты диссертации изложены в четырех публикациях, в том числе две статьи в изданиях, рекомендованных ВАК РФ.
Структура и объем работы.
Диссертация состоит из введения, 4 глав, заключения, списка цитируемой литературы из 101 наименования. Общий объем диссертации - 111страниц, включая 202 рисунка и 11 таблиц.
СОДЕРЖАНИЕ РАБОТЫ
а Во введении обосновывается актуальность темы, формулируется цель и задачи работы, определяется научная новизна и практическая значимость диссертации.
аа В первой главе приведен обзор исследований, посвященных аметодам расчета и экспериментальным данным по определению напряженно-деформированного состояния, критических и разрушающих нагрузок панелей из композиционных материалов.
Проблемой прочности и устойчивости слоистых пластин занимались аС.Г.Лехницкий, Э.И. Григолюк, А.П. Прусаков. Большой вклад в разработку новых методов расчета и проектирования конструкций из композиционных материалов внесли С.А.Амбарцумян, Н.А.Алфутов, Г.А.Ванин, В.В.Васильев, А.Н.Елпатьевский, В.А.Бунаков, Н.В.Баничук, А.А.Дудченко, В.И.Королев, Я.М.Григоренко, И.Ф.Образцов, П.А.Зиновьев, С.Н.Сухинин, В.Д.Протасов, Ю.В.Немировский и другие. В монографиях В.В.Васильева, И.Ф.Образцова, В.А.Бунакова, Н.А.Алфутова и П.А.Зиновьева сформулированы теоретические основы проектирования оптимальных композитных конструкций, найдены важные для практического приложения оптимальные структуры укладки волокон цилиндрических оболочек, баллонов давления, панелей и других конструкций.
Исследованию устойчивости и несущей способности прямоугольных композитных панелей посвятили свои работы А.А.Буштырков, С.А.Корзон, Biggers Sherrill, А.В.Лопатин, О.В.Митрофанов, Y.Zhang, D.A.Edwards, J.Mayersа и другие авторы. Были определены рациональные структуры армирования, позволяющие получить максимальные критические усилия в зависимости от видов нагружения, найдены зависимости дляа разрушающих усилийаа однородных ортотропных и анизотропных панелей,а проанализировано влияние параметра устойчивости от особенности строения КМ (геометрические размеры, жесткостные свойства, структура армирования), граничных условий и условия нагружения. аС помощью метода конечных элементов (МКЭ) Singha Maloy K., A.K.Noor, S.P.Engelstad, Donald J. Baker и другими исследовано влияние количества слоев и апорядка их укладки на критическое напряжение и закритическое поведение пластины после потери устойчивости.
Наряду с прямоугольнымиа широкое распространение получили панели других форм, в частности, ромбовидные и трапециевидные. Скошенные панели являются основными силовыми элементами кессонов крыльев и килей пассажирских и военных самолетов, обшивок авиационных и космических летательных аппаратов. Как известно из векторного анализа, для описания метрики Риманова пространства, к которому относятся скошенные системы, наиболее предпочтительной является декартова система координат, в которой определены компонентыа абсолютного ковариантного тензора 2-го ранга. Эти особенности скошенных систем определяют свойства тензоров деформаций и напряжений. В механике сплошной среды для исследования процесса деформирования бесконечно малого элемента Б.Н.Новожиловым, а позднее и А.А.Ильюшиныма использовались эйлеровы и лагранжевы криволинейные координаты, в которых определялись компоненты ковариантных и контравариантных тензоров деформаций и напряжений. Частным случаем криволинейных координат являются координаты косоугольного базиса. Тензоры деформаций в косоугольном базисе даны А.И.Лурье. Основные результаты по исследованию изгиба, устойчивости и колебаний изотропных пластин сложной формы были получены И.А. Биргером, K.Pandalai, М.А.Файзуллиной, М.С.Корнишиным, Н.О.Золотухиным и др. Были исследованы устойчивость и деформирование сжатых ортотропных косоугольных тонкостенных конструкций после потери устойчивости.
Обзор публикаций показал, что имеющийся теоретический и экспериментальный заделы ограничиваются устойчивостью и несущей способностью изотропных панелей, а также слоистых композитных прямоугольных пластина и не охватывают значительную часть конструкций других форм из композиционных материалов.
аа Во второй главе приводятся соотношения механики тонкостенных композитных конструкций и механики скошенных систем.
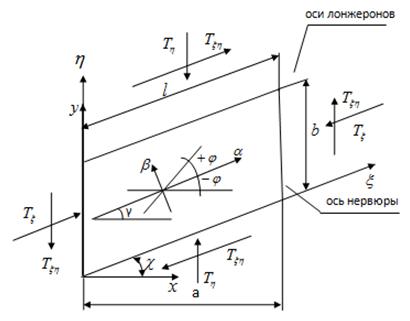
Рассматривается композитная панель крыла самолета, нагруженная в своей плоскости потоками сжимающих и касательных усилий. Панель в плане представляет параллелограмм (рис.1). Геометрия панели определяется шагом нервюр ![]() , расстоянием между осями лонжеронов
, расстоянием между осями лонжеронов ![]() аи углом скоса
аи углом скоса ![]() . Панель состоит из
. Панель состоит из ![]() аэлементарных слоев, расположенных симметрично по толщине пакета под углами
аэлементарных слоев, расположенных симметрично по толщине пакета под углами ![]() аили
аили ![]() ак некоторой оси
ак некоторой оси ![]() аотносительно которой задается схема армирования. Вводятся две ортогональные
аотносительно которой задается схема армирования. Вводятся две ортогональные ![]() аи одна декартова
аи одна декартова ![]() асистемы координат, относительно которой будут записываться все соотношения. С помощью системы координат
асистемы координат, относительно которой будут записываться все соотношения. С помощью системы координат ![]() абудем определять направление и структуру армирования слоев обшивки.
абудем определять направление и структуру армирования слоев обшивки.
 а
а
Рис.1
Записываются геометрически нелинейные соотношения, связывающие полные деформации панели ![]() ав ортогональной системе координат
ав ортогональной системе координат ![]() ас полными деформациями
ас полными деформациями ![]() ав декартовой системе
ав декартовой системе ![]()
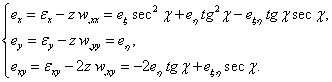 аа(1)
аа(1)
Устанавливаются зависимости между полными деформациями в слое композита а![]() аи деформациями панели в косоугольном
аи деформациями панели в косоугольном ![]() и ортогональном
и ортогональном ![]() базисах
базисах
![]() аа аа аа(2)
аа аа аа(2)
гдеа  ,
,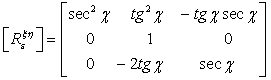
Каждый слой считается ортотропным, и для него справедлив закон Гука
![]() аа а(3)
аа а(3)
где аа ![]() - номер текущего слоя;
- номер текущего слоя;
![]() ,
, ![]() ,
,
 ,
,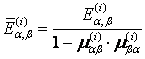 ,
,![]()
Записываются физические соотношения для усилий и моментов
![]()
![]() а (4)
а (4)
где ![]() и
и ![]() - квадратные симметричныеа матрицы мембранных и изгибных жесткостей, элементы которых определяются через обобщенные жесткости композитного слоя
- квадратные симметричныеа матрицы мембранных и изгибных жесткостей, элементы которых определяются через обобщенные жесткости композитного слоя ![]() аа(ij=11,12=21,14=41,22,24=42,44)
аа(ij=11,12=21,14=41,22,24=42,44)
![]() ,
, ![]() , аа
, аа
![]() ,
, ![]() - толщины от лицевой поверхности до слоев с номерами
- толщины от лицевой поверхности до слоев с номерами ![]() аи
аи ![]() . Обобщенные жесткости
. Обобщенные жесткости ![]() в косоугольном базисе выражены через известные обобщенные жесткости
в косоугольном базисе выражены через известные обобщенные жесткости ![]() ав ортогональном базисе
ав ортогональном базисе
![]() ,
,
где аа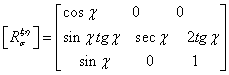 .
.
Формулируются граничные условия для сжимающих и касательных усилий, действующих на контуре панели
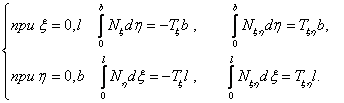 а а (5)
а а (5)
Выводятся уравнения равновесия в перемещениях
 а (6)
а (6)

Исходные соотношения дополняются функционалом энергииа
![]() а (7)
а (7)
Поскольку исходная задача решается в перемещениях, работу внешних сил апредставляем в форме Тимошенко
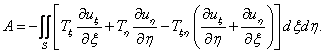
Для оценки прочности слоев композита в условиях закритического деформирования панели в диссертации был использован критерий Цая-Ву. Далее формулируется постановка задачи устойчивости и несущей способности скошенных композиционных панелей.
аа В третьей главе представлен метод расчета на устойчивость скошенных панелей с симметричной структурой армирования слоев. Исходная задача решается в перемещениях методом Рэлея-Ритца. Прогиб панели задается в виде ряда
![]() а,а аа а(8)
а,а аа а(8)
где ![]() а- амплитуда прогиба с числами полуволн m, n,
а- амплитуда прогиба с числами полуволн m, n, ![]() -собственные формы, определяемые граничными условиями задачи. Ониа выражаются через известные балочные функции Крылова для различных граничных условий. При решении задачи устойчивости пренебрегают докритическим напряженным состоянием
-собственные формы, определяемые граничными условиями задачи. Ониа выражаются через известные балочные функции Крылова для различных граничных условий. При решении задачи устойчивости пренебрегают докритическим напряженным состоянием ![]() аи деформациями координатной поверхностиа
аи деформациями координатной поверхностиа ![]() аа
аа![]() . Функционал энергии (7) принимает вид
. Функционал энергии (7) принимает вид
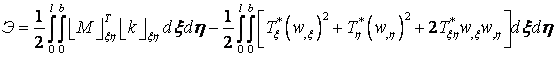 . аа
. аа
Подставив ряд (8) в функционал и воспользовавшись численным методом интегрирования по площади панели (производные от функций Крылова не являются ортогональными величинами), минимизируем получающееся выражение по каждому элементу вектора амплитуд ![]() . В результате приходим к однородной системе линейных алгебраических уравнений, которая в матричной форме примет вид
. В результате приходим к однородной системе линейных алгебраических уравнений, которая в матричной форме примет вид
![]() , аа(9)
, аа(9)
где ![]() а- квадратные матрицы коэффициентов при амплитудах с соответствующими индексами;
а- квадратные матрицы коэффициентов при амплитудах с соответствующими индексами; ![]() - соответственно векторы собственных значений при осевом сжатии, поперечном сжатии и сдвиге. Элементы квадратных матриц равны
- соответственно векторы собственных значений при осевом сжатии, поперечном сжатии и сдвиге. Элементы квадратных матриц равны
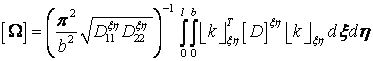 ,
, 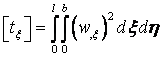 ,
,
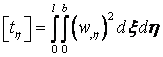 ,
, 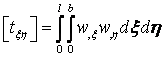 .
.
Критические усилия в момент потери устойчивости ищутся в виде
![]() ,а аа(10)а аа
,а аа(10)а аа
гдеа ![]() а-а безразмерные коэффициенты устойчивости;
а-а безразмерные коэффициенты устойчивости;
![]() ,
, ![]() ,
, ![]()
При определении собственных значений и последующих вычислений коэффициентов устойчивости ва зависимости от вида действующей нагрузки использованы методы преобразования подобия, реализованные в QR -алгоритме и процедуре Гессенберга. Проведенное сопоставление полученных результатов с данными других авторов показало, что наблюдаетсяа удовлетворительное совпадение результатов по коэффициентам устойчивости в большом диапазоне углов скоса панелей при различных граничных условиях.
Дальнейшие исследования в этой главе были посвящены анализу влияния углов скоса иа структур армирования слоев из углепластика на устойчивость панелей при сжатии ![]() , сдвиге
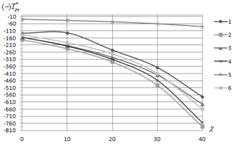
, сдвиге ![]() и комбинированном нагруженииа (совместное действие сжатия и сдвига).а Варианты граничных условий показаны на рис.2. На рис.3 приведены зависимости максимальных критических усилий при сжатииа
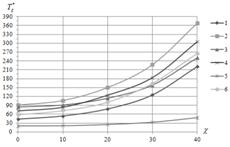
и комбинированном нагруженииа (совместное действие сжатия и сдвига).а Варианты граничных условий показаны на рис.2. На рис.3 приведены зависимости максимальных критических усилий при сжатииа ![]() (рис.3а), сжатии и сдвиге а
(рис.3а), сжатии и сдвиге а![]() (рис.3б) и сдвиге
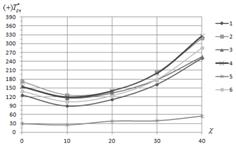
(рис.3б) и сдвиге ![]() (рис.3в),
(рис.3в), ![]() (рис.3г). Последние две зависимости показывают, что для скошенных панелей существенное значение имеет направление действия касательного усилия (положительное направление приведено на рис.1). Критические усилия, приведенные на рис.3, выбирались по критерию максимума из множества значений
(рис.3г). Последние две зависимости показывают, что для скошенных панелей существенное значение имеет направление действия касательного усилия (положительное направление приведено на рис.1). Критические усилия, приведенные на рис.3, выбирались по критерию максимума из множества значений ![]() , найденных при разных сочетаниях углов
, найденных при разных сочетаниях углов ![]() , а
, а![]() и фиксированных значениях угла скоса
и фиксированных значениях угла скоса ![]() .
.
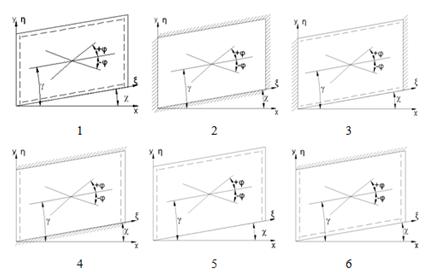
Рис.2
 аа
аа 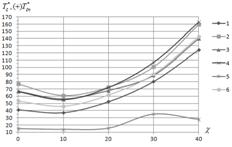
(а) (б)
(в)аа (г)
Рис.3
Проведенные исследования показали, например, что с увеличением угла скоса возрастают критические усилия осевого сжатия ![]() и сдвига
и сдвига ![]() ; при нагружении потоками касательных усилий заметным преимуществом обладает анизотропная структура армирования и т.д.
; при нагружении потоками касательных усилий заметным преимуществом обладает анизотропная структура армирования и т.д.
аа Четвертая глава посвящена решению геометрически нелинейной задачи о закритическом деформировании слоистойа симметричной панели и оценки ее несущей способности.
Закритический прогиб панели представляется в виде произведения неизвестной амплитуды ![]() аи собственной формы
аи собственной формы ![]()
![]() ,а (11)
,а (11)
где ![]() а - неизвестная амплитуда прогиба;
а - неизвестная амплитуда прогиба; ![]() - нормированный вектор, определяемый из системы уравнений (9). Аппроксимация (11) основана на предположении, что сразу после потери устойчивости форма поверхности панели подобна первой собственной форме
- нормированный вектор, определяемый из системы уравнений (9). Аппроксимация (11) основана на предположении, что сразу после потери устойчивости форма поверхности панели подобна первой собственной форме ![]() , соответствующей минимальному собственному значению - критическому усилию. Подставим (11) в уравнения равновесия в перемещениях (6), а производные от перемещений координатной поверхности заменим на центральные конечные разности. Тогда система уравнений примет вид
, соответствующей минимальному собственному значению - критическому усилию. Подставим (11) в уравнения равновесия в перемещениях (6), а производные от перемещений координатной поверхности заменим на центральные конечные разности. Тогда система уравнений примет вид
 аа (12)
аа (12)
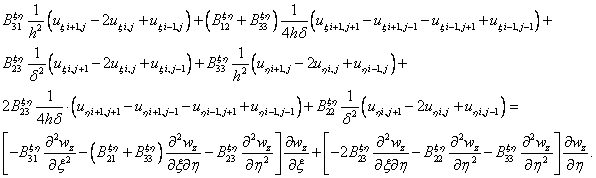
В качестве начального приближения для решения разностных уравнений (12) определяются перемещения на контурах панели с помощью интегральных статических граничных условий (5). Эта процедура позволяет исключить в разностной схеме формирование фиктивных точек. Найдя массивы перемещений на разностной сетке и воспользовавшись аппроксимацией (11), подставим эти данные в функционал энергии (7). Неизвестная амплитуда ![]() аанаходится из условия минимума полной потенциальной энергии закритического деформирования панели
аанаходится из условия минимума полной потенциальной энергии закритического деформирования панели
![]() аа (13)
аа (13)
где а![]()
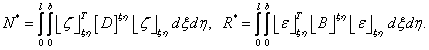
Решение имеет три корня, один из которых всегда действительный и равный ![]() . Последнее означает, что при нагрузках меньше критических усилий
. Последнее означает, что при нагрузках меньше критических усилий ![]() панель остается плоской. В точке бифуркацииа
панель остается плоской. В точке бифуркацииа ![]() все три корня действительны и равны
все три корня действительны и равны ![]() . При дальнейшем нагружении
. При дальнейшем нагружении ![]() возможны как плоское, так и искривленное состояния равновесия панели. Исследования показывают, что устойчивым будет искривленное состояние равновесия панели, амплитуда которого равна
возможны как плоское, так и искривленное состояния равновесия панели. Исследования показывают, что устойчивым будет искривленное состояние равновесия панели, амплитуда которого равна
![]() аа аа (14)
аа аа (14)
Построив зависимость контурное усилие-амплитуда прогиба, можно найтиа деформированное состояние панели в каждой точке, а затем - напряженно-деформированное состояние каждого слоя композита (2), (3). Для оценки несущей способности панели ва работе был использован критерий прочности Цая-Ву, позволивший определить предельные уровни сжимающих и касательных усилий, при которых в наиболее нагруженном слое композита произойдет исчерпание прочности материала
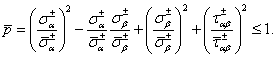 а (15)
а (15)
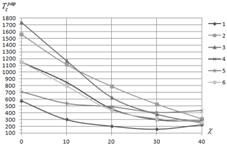
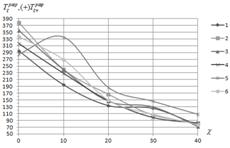
Численные результаты были получены дляа панелей с теми же граничными условиями, материалом слоев и формой контура, которые были рассмотрены в третьей главе. Наа рис.4 приведены зависимости максимальных разрушающих усилий от углов скоса ![]() (рис.4а),
(рис.4а), ![]() (рис.4б),
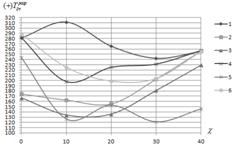
(рис.4б), ![]() (рис.4в),
(рис.4в), ![]() (рис.4г) при различных вариантах опирания кромок. Разрушающие усилия находились из условия максимума для множеств значений
(рис.4г) при различных вариантах опирания кромок. Разрушающие усилия находились из условия максимума для множеств значений ![]() , найденных при разных сочетаниях углов
, найденных при разных сочетаниях углов ![]() и
и ![]() и фиксированных значениях угла скоса панели
и фиксированных значениях угла скоса панели ![]() .
.
(а)а (б)
 а
а 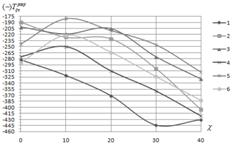
(в)а (г)
Рис.4
Исследования влияния геометрии панели, структур армирования и граничных условий, в частности, показали, что:
- наибольшей прочностью при сжатии обладают прямоугольные панели c однонаправленной структурой аармирования;
- наблюдается заметное падение несущей способности при увеличении угла скоса для панелей, нагруженных сжимающими нагрузками (рис.4а) и комбинированным нагружением (рис.4б) и т.д. Отмечается, что потерей устойчивости не исчерпывается несущая способность скошенной панели. Композитная панель продолжает воспринимать возрастающую нагрузку. К примеру, для шарнирно опертой панели с углом скоса 20? и структурой армирования ![]() соотношения между разрушающими и критическими усилиями составляют существенные величины как по сжатию, так и по сдвигу
соотношения между разрушающими и критическими усилиями составляют существенные величины как по сжатию, так и по сдвигу
![]() ,
, ![]() ,
,![]()
![]() .
.
ЗАКЛЮЧЕНИЕ
На основе проведенных в диссертации исследований сформулированы следующие основные результаты и выводы:
- Разработан прикладной метод определения устойчивости и несущей способности скошенных слоистых композитных панелей при сжатии, сдвиге и комбинированном нагружении с произвольными граничными условиями по контуру.
- Решение задачи устойчивости слоистой скошенной панели получено в перемещениях с использованием адаптированных к задачам на собственные значения функций Крылова.
- Построено решение геометрически нелинейной задачи в конечных разностях для определения закритических перемещений слоистой скошенной панели с произвольными граничными условиями.
- Отмечено существенное влияние на устойчивость и несущую способность скошенных панелей направления действия касательных усилий.
- Исследовано влияние углов скоса, схем армирования и граничных условий на критические усилия устойчивости панели при действии сжимающих и касательных усилий, а также при комбинированном нагружении. Отмечается, что в случае сжимающих усилий увеличение углов скосаа приводит к росту критических усилий сжатия панелей. При действии на панель с большими углами скоса потоков касательных усилий наблюдается существенное снижение влияния граничных условий на величину критических нагрузок.
- Исследовано влияние углов скоса, схем армирования и граничных условий на несущую способность слоистых композитных панелей при закритическом деформировании. Установлено, что наибольшей прочностью после потери устойчивости при сжатии, а также при комбинированном нагружении сжатием и сдвигом обладают прямоугольные панели. При действии на панель касательных усилий аее несущая способность зависит как от углов скоса, так и структуры армирования и граничных условий. Влияние указанных параметрова имеет разнонаправленный характер, поэтому не удается выявить наиболее существенный из них.
- Из условия максимума критических усилий определены рациональные структуры армирования скошенных слоистых панелей. Однако в случае потери устойчивости панели выявлены отличные от найденных структуры, обеспечивающие амаксимальную несущую способность.
Основные результаты диссертации опубликованы в работах:
Публикации в изданиях, рекомендованных ВАК РФ
- Азиков Н.С., Гайдаржи Ю.В. Устойчивость слоистых скошенных панелей. // Механика композиционных материалов и конструкций. - 2010. - Т.16. - №3. - С.361-368.
- Азиков Н.С., Гайдаржи Ю.В. Закритическое поведение скошенных композитных панелей // Механика композиционных материалов и конструкций. - 2011. - Т.17. - №3. - С.411-420.
Другие публикации
- Азиков Н.С., Гайдаржи Ю.В. Устойчивость косоугольных композитных панелей при сжатии и сдвиге. XXXVII Гагаринские чтения. - М.: МАТИ,а 2011.-Т.5.- 240с.
- Азиков Н.С., Гайдаржи Ю.В. Несущая способность косоугольных композитных панелей при сжатии и сдвиге. XXXVII Гагаринские чтения. а
М.: МАТИ, 2011. -Т.5. -240с.
 Авторефераты по темам >>
Разные специальности - [часть 1] [часть 2]
Авторефераты по темам >>
Разные специальности - [часть 1] [часть 2]
