Все научные статьи
Все научные статьи
Кожевникова И.А., Швейкина В.И. Уточненная стохастическая модель колебаний уровня Каспийского моря
Научная статья
Электронный научный журнал ИССЛЕДОВАНО В РОССИИаа 1450а Уточненная стохастическая модель колебаний уровня
Каспийского моря
Кожевникова И.А.(1), Швейкина В.И. (shveik@aqua.laser.ru)(2)
(1) Московский государственный университет им. М.В. Ломоносова, (2) Институт водных проблем Российской академии наук
Предлагается новый метод построения стохастической модели колебаний уровня Каспийского моря, основанный на аппроксимации плотности распределения вероятностей смесью трех нормальных распределений. Оценки адекватности модели показывают ее преимущество перед моделями, использующими построение модели на основании нелинейной регрессии.
Введение. В данной статье рассматривается проблема построения математической модели, описывающей динамику колебаний уровня Каспия. Проблема адекватного описания этого процесса была актуальной, когда уровень неожиданно и стремительно падал и остается такой в наше время, которое характеризуется заметным глобальным потеплением и все возрастающим подъемом уровня мирового океана.
Статистический анализ наблюденных данных показывает, что реальное распределение вероятностей не является нормальным, т.к. имеет несколько мод. Впервые о многомодальности плотности распределения уровня Каспия и, следовательно, об отличии этого распределения от нормального было отмечено в работах В.И. Найденова [5]. Отмеченный феномен является всеобщим: негауссовость распределений уровня замкнутых водоемов проявляется для всех исследованных водоемов (озера Чад, Чаны, Большое Соленое, Балхаш, Ханка), а также присущ многим другим природным явлениям, имеющим в своих колебаниях несколько устойчивых состояний.
Ежемесячные наблюдения за уровнем Каспийского моря с 1900 по февраль 2006 г. показывают появление третьего устойчивого уровня, в окрестности которого уровень моря находится более 20 лет. Значение уровня, равное приблизительно -27 м абс, до последнего времени авторы считали неустойчивым [4]. С этого уровня колебания моря, индуцированные внешним воздействием, неминуемо должны были приблизиться к устойчивым состояниям -26 или -28 м абс. Однако в последние 20 лет такого скачка уровня не зафиксировано. По сравнению со всем интервалом имеющихся наблюдений в 175 лет отрезок в 20 лет не слишком большой, чтобы окончательно считать значение уровня устойчивым. Но такие косвенные характеристики, как гистограмма эмпирических наблюдений (рис.1) и фазовый портрет (рис.2) имеющихся данных показывают значимые скопления данных около значения уровня -27 м абс.
и.о
О
о
н о
S
н о ft о я
0.5 0.4 0.3 0.2 0.1
-29а -28а -27а -26а -25
Уровень, м абс.
Электронный научный журнал ИССЛЕДОВАНО В РОССИИаа 1451а Рис. 1. Гистограмма данных наблюдений за уровнем моря в г. Махачкале.
0.4
|
Iаа 0.2
<и о
Sа ^а О
К йаа и
-0.2 -0.4 |
а
са
-30а -29 -28 -27 -26
Уровень, м. абс
Рис. 2. Фазовый портрет уровня Каспийского моря.
В статье [4] обосновано представление о колебаниях уровня Каспия как о хаотическом процессе, чьи переходы с одного устойчивого состояния в другое поддаются только вероятностной оценке. Как правило, колебания уровня замкнутого водоема рассматриваются как случайный процесс. В статье сделана попытка показать, что колебания Каспия обусловлены взаимодействием нескольких случайных процессов, каждый из которых описывает лопределенную компоненту изменчивости, обусловленную влиянием некоторого природного фактора. Таким образом, мы получаем многомерное описание колебаний уровня Каспия.
Получить модель колебаний уровня моря можно разными способами. Первый способ, разработанный авторами, основан на аппроксимации исходных данных. Полученное приближение колебаний используется в качестве коэффициента сноса в уравнении Фоккера-Планка-Колмогорова (ФПК), решение которого дает плотность распределения. Такой способ, использующий нелинейную регрессию 5-го порядка, применен при построении модели колебаний Каспия в [4]. Дополненные среднемесячные данные по г. Махачкале, оцененные с помощью нелинейной регрессии [1], по-прежнему демонстрировали два устойчивых уровня и один неустойчивый. Интересно отметить, что ряд среднегодовых значений уровня Каспия по г. Баку, для которого также была построена нелинейная стохастическая модель с использованием нелинейной регрессии, обнаруживает три устойчивых состояния и два неустойчивых (переходных). Значения всех корней регрессии оказались действительными, хотя сама регрессия не очень четко фиксирует эти состояния, два корня, соответствующие значениям уровня -28,31 и -28,17 м абс. мало различимы. В статье предложен еще один способ получения модели, четко фиксирующий наличие трех устойчивых состояний. Идея заключается в решении обратной задачи: аппроксимируются не исходные наблюдения, а эмпирическая плотность вероятностей, на основе которой строится модель.
Задача статистического разделения смесей вероятностных распределений
Смешанное распределение вероятностей характерно для многих процессов, описывающих природные явления. В гидрологических исследованиях, как правило, используется какое-нибудь одно распределение вероятностей, с помощью которого описывается весь ряд наблюдений. Конечно, выбор распределения зависит от задачи, которую при этом решают. Если, например, интересует в основном правильное описание вероятности редко встречающихся событий, то рациональнее использовать степенное распределение [2,6]. По речному стоку ряды наблюдений достаточно хорошо описываются гамма распределением, а в некоторых случаях 3-х параметрическим распределением Вейбулла,
Электронный научный журнал ИССЛЕДОВАНО В РОССИИаа 1452а которое в гидрологических исследованиях принято называть распределением Крицкого-Менкеля. Для построения смешанного распределения, кроме упомянутых выше, могут быть использованы и многие другие распределения, например, экспоненциальные, пуассоновские, биномиальные и др. [3]. Оценка теоретических параметров смешанного распределения также может быть осуществлена различными методами, например, методом моментов, методом максимального правдоподобия, методом наименьших квадратов, некоторыми видами минимаксных оценок, графическими методами и т.д. В статье использованы гауссовские распределения, а для предварительного оценивания параметров и получения начальной точки итеративного метода - графический метод.
Таким образом, имея на сегодня три устойчивых состояния, исследуемый процесс можно аппроксимировать смесью трех нормальных распределений. Применяя строгие математические процедуры, можно провести кластерное разделение ряда наблюдений за уровнем моря, однако простой здравый смысл позволяет выделить три периода, когда колебания уровня происходили около одного из устойчивых состояний. Первый период, включающий 37 лет наблюдений, приходится на начало ряда, когда море тяготело к уровню -26 м абс, второй период включает резкое падение уровня моря и его стабилизацию около -28 м абс, и третий, содержащий наблюдения с 1986 г., характеризуется колебанием уровня около -27 м абс. Для каждого из этих трех периодов по критерию Д'Агустино была проверена и принята гипотеза о подчинении колебаний нормальному закону. Так как указанный критерий редко применяется при исследовании гидрологических явлений, опишем его более подробно [9]. Рассмотрим натурные данные Хх...Хп и построим для них вариационный ряд Х^<Х(2)<...<Х(Ду Определим выборочную
Т
функцию D = ЧЧ,
п S
где
s^-t^-xf
Ча 1аа "
П ,-=1
Ваа [9]аа показано,а чтоа еслиа выборк Хх...Хпаа взятаа иза нормальногоа распределения,а то
асимптотическиеаа значения математического ожидания и стандартного отклонения выборочной функции D соответственно равны
?(?>)л Ч - = 0,28209479,
Тогда выборочная функция
JЩ(D)
Y
0,02998398
4п
D-E(D)
имеет при и^-оо нулевое математическое ожидание и единичную дисперсию. Если выборка не принадлежит нормальному распределению, значение Y будет отличаться от нуля и может быть, и положительным и отрицательным. Методом математического моделирования было установлено: если альтернативное распределение имеет эксцесс, больший, чем у нормального распределения, тогда значение Y будет больше нуля. В [9] приведены таблицы, дающие критические значения для различных уровней значимости в случае выборок больших и малых длин. Например, для выборки верхнего уровня (-26 м абс.) критерий Д'Агустино дает значение -0.137, заключенное в доверительных пределах (-
Электронный научный журнал ИССЛЕДОВАНО В РОССИИаа 1453а 1.661; 0.759). Это означает, что на уровне значимости 0.2 временной ряд первого периода имеет нормальное распределение. Аналогично, на уровне значимости 0.2 установлена нормальность распределения для выборок второго и третьего периодов. Таким образом, задача аппроксимации истинного распределения сведена к статистическому определению смеси распределений, которое имеет неизвестные параметры.
Теоретические моменты смешанного распределения выражаются через первый и второй моменты каждой компоненты смешанного распределения [7].
/(*)=pJi (*; м, en2)+аЛ (*; м> ст2)+ 0 - а - а)/3 (х; м> Gl \
гдеаа /(х;//.,сгг2]-аа плотностьаа /'-ойаа компонентыаа смешанногоаа распределения; pt-аа вес
соответствующей компоненты. Чтобы оценить параметры каждой компоненты и веса компонент необходимо вычислить моменты смешанного распределения вплоть до восьмого порядка. Приведем формулы для моментов гауссовского распределения #(ы,<72)[8]:
Щ =ju,
т |
y=y+гCf<72V-2*(2*-l)!,аа j>2,
к=\
где j - порядок момента гауссовского распределения, [2к -1)!! - произведение нечетных чисел от единицы до (2к -1) включительно. Тогда формулы для вычисления моментов j -го порядка смешанного распределения с q компонентами имеют вид:
т
ч ,1=ZAA'а Ч = \
2=1
т
/=1
к=\ |
м/ + 1ёс?}км/~2к(2*-1У-
,аа 7^2.
я I 2=1 |
2>,-=1>а А=1-А"А-
i = AM + AM + О " А " А)м,
т2 = А (м2 + cWx) + А (м2 + С 2^2) + О " А " А Хм2 + С22сгз),
щ = а(м3 + Q2c"2m)+а(м3 +Q2cr22)+(1-A - аХм3 + Q2c"32),
да4 = рх {$ + С^о-т2//!2 + С\о^ жl-3)) + p2(t4+ С\о\& + С\а\ Х 1 Х з) + (1 -рх -р2)(А4(//3,ст3)),
да5 = а(м5 +Q2c"2m3 +QVM1 -1-з)+^2(А5(//2,сг2))+(1-а -^2ХА5(//3,сг3)), Щ6 = А (мб + С' + Q4X Х 1 Х 3 + Cfo6 Х 1 Х 3 Х 5)+ р2(Аб(//2, ст2)) + (l - Pl- р2)А6{/иъ, а3),
Электронный научный журнал ИССЛЕДОВАНО В РОССИИаа 1454а
т
7 = р1 Щ + CjCrfju^ + Cj<j*juf Х 1 Х 3 + Cyof/Zj Х 1 Х 3 Х 5)+ р2А7{ju2,а2) + В7.
m8=Pli[juf+Ci^juf+C^al4ju^h3 + Clafju^h3-5 + Claf-h3-5-7) + P2A8(ju2,a2) +
Bs
гдеВк=(\-Р1-р2)Ак,аа ? = 7,8,аа 4= l4 + ZC?^kt4~U'(2*-l)!!,аа / = 4,...,8
?=1
Начальные моменты в левой части уравнений оцениваем по выборке, применяя формулы:
1аа п
Вычисления ведутся, исходя из минимума функции
![]()
![]() е=1
е=1
7 = 1
m. - m. ifi
С помощью итерационных методов решения системы алгебраических уравнений получили следующие значения оценок параметров смешанного распределения вероятностей.
Таблица. Оценки параметров q компонент смешанного распределения.
q = \ |
q = 2 |
q = 3 |
|
ч |
jux = -26.0085 |
ju2 = -28.24 |
ju3 =-27.0713 |
, |
Gx =0.316 |
a2 = 0.363 |
cr3 = 0.256 |
pq |
px =0.37 |
A =0.45 |
p3 =0.18 |
Полученныеаа значенияаа параметроваа позволяютаа построитьаа смешанноеаа распределение, которое хорошо согласуется с эмпирическим (рис.3).
Электронный научный журнал ИССЛЕДОВАНО В РОССИИаа 1455а 0.7
|
0.6аа -
0.5аа -
0.4
0.3аа -
0.2
0.1аа -
-29.5 -29
-28.5 -28 -27.5
-27 -26.5 -26 -25.5 -25 Уровень, м абс.
Рис. 3. Смешанное распределение вероятностей для уровня Каспийского моря (сплошная линия - смесь трех нормальных распределений, маркеры - значения гистограммы).
Традиционно по модели, в качестве которой взят диффузионный процесс, получают уравнение ФПК для стационарной плотности вероятностей. Полученная стационарная плотность не совсем совпадает с оценкой по выборке. В статье впервые решается задача обратного преобразования одного из коэффициентов уравнения ФПК, а затем строится уточненная модель.
Таким образом, получена оценка плотности распределения вероятностей в виде смеси трех гауссовских распределений с 8-ю оцененными параметрами. Рассмотрим непрерывную модель колебаний уровня моря в виде диффузионного процесса
dZt
dU dZ
dt + <jdWt
(1)
где Ut - потенциал Каспийского моря, - dU/dZ - коэффициент сноса, а -коэффициент диффузии, Wt- стандартный винеровский процесс. Тогда соответствующее диффузионному процессу (1) уравнение ФПК имеет вид
dp(y,t\x)_ d[Q(y)p(y,t\x)] g2d2(p(y,t\x))
dt
ду
ду2
Стационарнаяаа плотностьаа вероятностейаа уровня,аа полученнаяаа ваа результате решения уравнения ФПК для (1) и при dp/dt = 0 выражается следующим образом:
Ps (Х) = =Т еХР =Г j Ф(иУЩ
\<Уаа _ш
'а Х1Ша Ч Х Ч Хтах >
(2)
где С - нормирующий множитель,аа аа =0.011. Подставляя в (2) выражение для
коэффициента сноса ф(х)=------- Ч, получаем
dx
Электронный научный журнал ИССЛЕДОВАНО В РОССИИаа 1456а
![]()
С |
(х)==гехр -=2"?/(х)
Vаа о
Выразим из последнего выражения U(x).
ЧU(x) = ln Ч -lnps(x),
Стационарная плотность, как правило, отличается от эмпирической гистограммы. Решим обратную задачу, а именно: возьмем в качестве стационарной плотности распределения функцию, достаточно хорошо аппроксимирующую эмпирическую гистограмму f(x). Тогда, подставляя ее в последнее выражение для потенциала, будем иметь:
^U(x)=\n^-\nf(x),
аа
или
г/(x)=гlln_C
2аа */М
Используем выражение потенциала для нахождения нового коэффициента сноса уравнения ФПК, решением которого является функцияа f{x), по следующей формуле
<&Х(*) =
dU _ aа f'(x) dxаа 2аа f(x)
Теперь модель колебаний уровня Каспийского моря выражается вновь полученным стохастическим уравнением
dXt = Ч ЦЩ- dt + adWt 2аа /(X)
где
2al
V2;r k=l
Ч3
Ok
2al
В ранее предложенной авторами модели [4] коэффициент сноса выражался полиномом 5-ой степени. Теперь он выражен более сложным образом, но точнее описывает регрессионное облако точек. Используя полученную модель, была получена траектория (рис.4), качественно похожая на кривую колебаний уровня Каспийского моря (рис.5).
Электронный научный журнал ИССЛЕДОВАНО В РОССИИаа 1457а -25.6 -|
0а 500 1000аа 1500аа 2000
Время, отн.ед.
Рис. 4. Моделированная траектория.
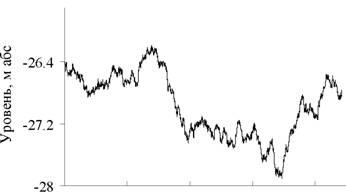
|
а
-25.5
-27.5
-29.5
1900 1940 1980 2020
Время, годы
Рис. 5. Уровень Каспийского моря.
Адекватность полученной модели исходным данным характеризует остаточная сумма квадратов значений, каждое из которых равняется разности наблюденного и высчитанного по модели. Эта сумма получилась равной 9.87. Остаточная сумма квадратов, посчитанная по нелинейной регрессии в виде алгебраического полинома 5-ой степени для данных г. Махачкалы, составляет 11,81.
Заключение. Предложенная модель четко фиксирует третий устойчивый уровень. Для уровня Каспийского моря возможен только вероятностный прогноз, так как его колебания имеют хаотические режимы. Приближаясь к точке бифуркации, уровень как самоорганизующаяся система сам выбирает свой дальнейший путь, предсказать который можно только вероятностно. Так как в колебаниях уровня вполне вероятен хаотический режим, вся траектория его изменения очень зависит от начальных условий. Как показал, например, В.И. Найденов, а до него американский метеоролог Э. Лоренц, для хаотических систем расхождение в начальных данных порядка 10" приводит к совершенно различным видам колебаний. В настоящее время в оценочных докладах Межправительственной группы экспертов по изменению климата приведены самые разные виды прогноза изменения уровня Каспия. Прогнозируется как подъем уровня, так и его падение, а также стабилизация уровня около современного его значения -27 м абс. Разные виды прогноза зависят от начальных условий, что еще раз подтверждает хаотический характер колебаний уровня Каспия. Колебания уровня замкнутого водоема так же, как и всей гидросферы, нелинейные, поэтому не только разные начальные условия, но и изменение только одного какого-нибудьа параметраа са течениема времениа неминуемоа приводита к радикальному
Электронный научный журнал ИССЛЕДОВАНО В РОССИИаа 1458а изменению всей системы. В существующих моделях общей циркуляции атмосферы и океана пока этот принципиально важный факт не учитывается.
Появление третьего устойчивого уровня в колебаниях Каспийского моря приводит к новым пока не решенным математическим задачам определения времен перехода от одного устойчивого состояния к другому. В потенциальной функции, описывающей движение идеальной точки, возникают три ямы. Расчет расщепленных вероятностей нахождения точки в одной из них требует дальнейших исследований.
Второй способ получения модели колебаний уровня Каспия, разработанный авторами, предложен впервые. Решение уравнения Фоккера-Планка-Колмогорова выражается через коэффициенты сноса и диффузии. Основная задача заключается в точном определении этих коэффициентов. Однако можно эту тонкость обойти, решая обратную задачу через аппроксимацию плотности распределения вероятностей. При этом решение получается адекватно отражающим некоторые характерные свойства исходных данных, в частности четко фиксируется число устойчивых состояний.
итература
- Айвазян С. А. Исследование статистических зависимостей. М. Металлургия. 1968. 258 с.
- Долгоносое Б.М., Корчагин К.А. Нелинейная стохастическая модель формирования ежедневных и среднемесячных расходов воды в речных бассейнах.//Водные ресурсы. 2007. т. 34. № 6. С. 662-672.
- Исаенко O.K., Урбах В.Ю. Разделение смесей распределений на их составляющие. В кн. Итого науки и техники. Теория вероятностей. Математическая статистика. Теоретическая кибернетика. Т. 13. ВИНИТИ. Москва. 1976. С. 37-58.
- Кожевникова И.А., Швейкина В.И. Нелинейная динамика колебаний уровня Каспийского моря. //Водные ресурсы. 2008. Т. 35. № 3. С. 313-320.
- Найденов В.И.,а Подсечин В.П.а Оа нелинейнома механизмеа колебаний уровня водоемов//Водные ресурсы. 1992. №6. С. 5-11.
- Найденов В.И., Швейкина В.И. Гидрологическая теория глобального потепления климата Земли. Метеорология и гидрология. № 12. 2005. С. 31-38.
- Хальд А. Математическая статистика с техническими приложениями. М. Иностранная литература. 1956. 664 с.
- Ширяев А.Н. Вероятность. 2004 М., Наука. 418 с.
- D'Agostino R.B. An omnibus test of normality for moderate and large size samples//Biometrika. 1971. V. 58. № 2. Pp. 341-348.
 Все научные статьи
Все научные статьи