Сикорский Д.А. Метод оценки уровня турбулентности атмосферы

Научная статья

Электронный журнал ИССЛЕДОВАНО В РОССИИаа 824

Объект наблюдения

Среда распространения

Зрительный анализатор

Рис. 1. Обобщенная структурная схема ОЭТ

В качестве турбулентной среды выступает атмосфера. Ее оптические турбулентные свойства обусловлены случайными изменениями коэффициента преломления по трассе наблюдения, что вызывает искривление волнового фронта и, следовательно, приводит к размытию изображения в картинной плоскости ОЭА. Как правило, аппаратура наблюдения вышеотмеченных систем работает с временами накопления Тн=1-5 мс. Эти времена значительно меньше временного радиуса корреляции случайных турбулентных возмущений. В этом случае можно считать, что съемка объекта наблюдения осуществляется через так называемую "замороженную атмосферу". На рис.2 в одномерной геометрической интерпретации иллюстрируются варианты формирования суммарной функции рассеяния точки оптической системы и "замороженной атмосферы".

Р. Хафнагель [1] оценил функцию распределения интенсивности кружка рассеяния турбулентной атмосферы при наблюдении в полдень через всю её толщу для видимого диапазона. В дальнейшем кру-

Электронный журнал ИССЛЕДОВАНО В РОССИИаа 825

Турбулентная среда

Плоскийфронт, формируемыйточечнымисточником

Неискаженныйфронтпри отсутствиитурбулентности

Оптическаясистема

ФРТоптическойсистемы

ЧжЧ

/:-".u- Л.ур^улентн-ая1 среда *&*#

жж ж ж__________________

liii___ !_

V5^3

к'жж'.'-Х' "Турбулентная'

_"J____ I___ "аа I |Г ' 'аа '_______ ~^1а ж 'жХ_________ ^ "жаа ж 'ч-

Фронты, искаженные "замороженной" турбуентнойатмосферой

/Vаа /\

Суммарныефункциирассеянияточкиоптическойсистемыитурбулентнойсреды

Рис. 2. Геометрическая одномерная интерпретация процесса формирования функции рассеяния точки при различных турбулентных искажениях, вносимых "замороженной атмосферой"

Электронный журнал ИССЛЕДОВАНО В РОССИИаа 826

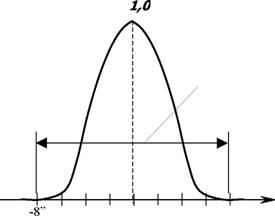
Относительная

интенсивностьв

среднемкружке

рассеяния

Угловойрастворкружкарассеяния

Угловоерасстояниеотцентра усредненногокружкарассеяния

угл. сек

-4" 'аа 0аа 'аа +4"а +8"

Рис. 3. Распределение интенсивности в кружке рассеяния турбулентной среды при наблюдении в полдень через всю её толщу

Автором с целью юстировки зеркального телескопа с фокусным расстоянием 1 м осуществлялось наблюдение удаленного (Lл2,5 км) квазиточечного объекта на поверхности Земли по слабонаклонной (ф=5) открытой трассе. Результаты измерений ФРТ телескопа показали, что раствор этой функции значительно превышает расчетное значение. По мнению автора это связано с негативным влиянием турбулентности среды распространения.

В связи с этим возникла необходимость количественной оценки степени данного влияния в конкретных условиях наблюдения.

Для проведения этих оценок был использован известный инструментарий [2], описание которого приводится ниже.

1. Метод оценки пространственных свойств функциональной пары оптическая система+фотоприемник по обобщенной пограничной кривой

Для пояснения сути метода определим распределение выходного сигнала фотоприёмного устройства (ФПУ) с пространственно-регулярной дискретной структурой его элементов.

Пусть Н(х,у) - двумерное распределение яркости объекта наблюдения. Тогда распределение сигнала в непрерывном (гипотетическом) фотоприемнике

Q*(x,y)=к Н(х,у)**0(х,у)**Р(х,у),

(1.1)

Электронный журнал ИССЛЕДОВАНО В РОССИИаа 827

здесь Ax, AY - периоды решетки ФПУ по соответствующим осям;

Afx, Afy - случайные фазы выборки.

Функция S5(x,y) называется дискретизирующей функцией или функцией выборки.

Суть методики сводится к оценке суммарной апертурной функции Т(х,у), равной свертке апертурных функций ОС и элемента ФПУ. Будем считать, что все приведенные апертурные функции пространственно инвариантны.

Учитывая (1.1), а также то обстоятельство, что преобразование Фурье свертки нескольких функций равно произведению преобразований Фурье свертываемых функций, можно записать:

T(v,m)=0(v,M) P(v,M). (1.4)

Центральная предельная теорема утверждающая, что закон распределения суммы случайных величин неограниченно приближается к нормальному закону, имеет аналог в теории линейной фильтрации: произведение п пространственно-частотных характеристик отдельных звеньев линейной системы стремится к гауссовой форме, когда п становится большим.

Указанное обстоятельство придает особое значение гауссоиде вращения, как универсальному и достаточно точному описанию пространственно-частотных свойств реальных оптико-электронных приборов.

Математическая запись нормированной гауссоиды вращения представляется в виде:

~~2

,2 \(а Д2 Л

ехр

(1.5)

2о

Т(х,у)=ехр

2о

Электронный журнал ИССЛЕДОВАНО В РОССИИ

828

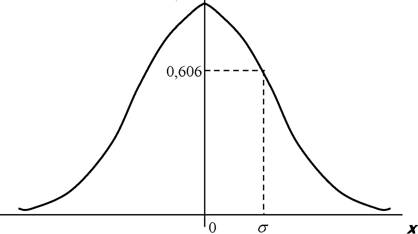
Сечение гауссоиды вращения по оси х представлено на рис.1.1.

1,0аа м

Рис. 1.1. Сечение гауссоиды вращения. Здесь о - параметр гауссоиды

Наличие Т(х,у) изображающей системы с о>0 приводит к тому, что резконтрастное распределение яркости объекта Н(х,у) преобразуется в размытое изображение. Степень размытия тем больше, чем больше величина о.

Пусть объект Н(х,у) имеет двумерное распределение яркости резкого края:

0 при х<х0,

1 при хп >х,

НР.к.(х,у) =

(1-6) 1/2 при х0=0,

для любых у.

Функция распределения сигнала резкого края в непрерывном фотоприемнике Qp.K.(x) п0 оси х за счет наличия апертурной функции Т(х,у) однозначно связана с ней и определяется её видом.

Определим распределение Qp.K.(y) по оси У и Qp.k.(x) п0 оси х-Функции Qp.K.(x) и Qp.K.(y) называются пограничными кривыми резкого края (по соответствующим направлениям).

Значение двумерной функции распределения сигнала изображения в точке с координатами х, у в непрерывном фотоприемнике находится в соответствии с выражением (1.1).

Найдем производную по оси х, т.е. в направлении, перпендикулярном границе резкого края.

5Qp.K.(x>y)

дх

_д_ дх

+00+00

{а jHp.K.(xi,yi)-exp

(x-Xl)2

Электронный журнал ИССЛЕДОВАНО В РОССИИ

829

ехр

(y-yi)2

2а2

chqdy]

(1.7)

Так как НРК (х,у) не зависит от у и интегрирование осуществляется по переменным Xi yi, а также учитывая (1.5), последнее выражение запишется в виде:

Эхаа I

ехр

(x-Xl)2

+оо

6х1 J ехр

(У-Yi)2 2о2

dy1 =

= V2noexp

2о'

(1.8)

где {QJx-обозначает операцию дифференцирования функции ( ) по

переменной х.

Поскольку производная пограничной кривой резкого края по направлению х определяется выражением (1.8), то

( х ^ л/2о.

Xаа (аа t2аа N\

ехр

-ооа V

(1.9)

dt = erf

<&c(x)=4uJ

2а'

2по

Найдем производную функции распределения <Зр.к.(х'У) по оси у,

совпадающей с границейаа резкогоаа края

dQp.K.(*,yL д

дуду

+ GO+GO

| |Hp.K.(xi,yi)exp

2а2

ехр

(У-Yi)2 2а2

dXidy!

(1.10) Учитывая те же обстоятельства, отмеченные при нахождении производной <Зр.к.(х/У) по оси х, запишем:

+оо

dXlJ

+оо

{ехр

о |п

SQ?.K.(x,y)аа +

ах

-о Х ехр

(x-xt)2 2а2

" (у-уд)2

2а2

ехр

(y-yi)2

2о2

JJ Y

dy1 =

(1.11)

Поскольку производная функции <Зр.к.(х/У) резкого края по направлению у равна нулю, то сама функция Qp.K.(y) есть величина, постоянная для любых х.

Если в поле зрения изображающей системы присутствует объект, описанный выражением (1.5), то, измерив одномерную функцию распределения сигнала от этого объекта, формируемого в непрерывном фотоприемнике в направлении, перпендикулярном границе резкого края,а иа взяв от нее производную,а можно определить апертурную

Электронный журнал ИССЛЕДОВАНО В РОССИИаа 830

%жж

q;j

х)

......... 4

*.........

......... 4

Е^-"*""

""*"'...... i

--------------- <

Р"

->>

					,... а QpAx)
т...						------------- >

Электронный журнал ИССЛЕДОВАНО В РОССИИаа 831а

QpjJx)

<Ж.М

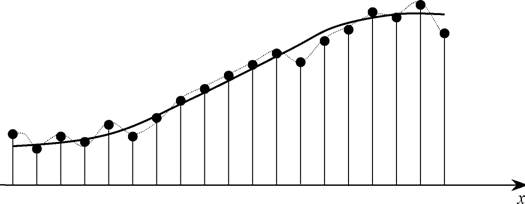
Рис.1.3. Сглаживание функцииа Qpг(x) (пунктирная линия) по большому количеству ее отсчетов в условиях действия шума

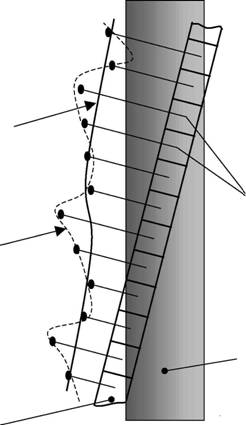
Из выделенных объектов отбираются такие, у которых их прямолинейная граница расположена под малым углом ср по отношению к одному из направлений пространственной структуры приемника (рис.1.4).

Структура приемника такова, что элементы образуют столбцы и строки, расположенные ортогонально по отношению друг к другу. За направления пространственной структуры приемника выбраны направления строк и столбцов. Практика использования оптико-электронных систем показала, что трудностей в выборе пригодных объектов на получаемых изображениях нет.

К таким объектам относятся: резкие края крыш, стены домов, прямолинейные участки автомобильных магистралей, прямолинейные участки береговой линии водоемов и т.п.

Ниже рассматривается случай расположения границы смежных полей изображения резкого края под малым углом к направлению

Электронный журнал ИССЛЕДОВАНО В РОССИИаа 832

столбцов. При этом последующие рассуждения полностью справедливы для случая, когда граница объекта ориентирована под малым углом к направлению строк.

Из всей совокупности столбцов фотоприемника выбирают такой j-й столбец, элементы которого полностью пересекают границу изображения выбранного объекта (рис.1.4). Выборкиэтогостолбцаобразуют, такназываемую, обобщеннуюпограничнуюкривую (ОПК).

Рассматривая соседние значения выборок ОПК, отмечаем, что они отличаются на малую величину, т.е. сильно коррелированы. Это позволяет, как было отмечено выше, в условиях действия шумовой компоненты эффективно проводить сглаживание ОПК без потери полезной информации.

Поиск параметра о гауссоиды вращения осуществляется в следующем порядке.

Определяется область последовательных выборок j-ro столбца, которая несет информацию о степени размытия резкого края.

В соответствии с (1.9) огибающая сигналов элементов выбранного столбца аппроксимируется (например, по минимуму СКО) функцией

вида erf Ч-аа путем подбора параметра о' (x'=x/sin^).

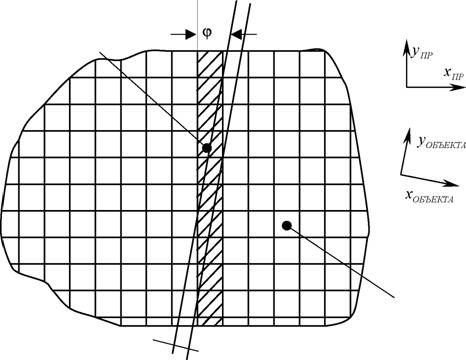
] -йстолбец

Одиночныйэлементфотоприемника

Размытаяобласть' резкогокрая

v2o')

Рис.1.4. Структура приемника определяет пространственно регулярный характер выборки распределения сигнала, формируемого в непрерывном приемнике. Из всей совокупности столбцов приемника

Электронный журнал ИССЛЕДОВАНО В РОССИИаа 833

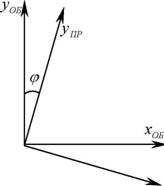
Аппроксимирующая ОПКфункция

ПериоданализирующейдискретизацииА

Огибающая ОПК

Размытаяобласть резкогокрая

]-йстолбец

Рис. 1.5. Геометрическая интерпретация процесса определения параметра апертурной функции

ОПК

2. Метод оценки уровня турбулентности атмосферы по

Электронный журнал ИССЛЕДОВАНО В РОССИИаа 834

*-#*

*-№'Х

Турбулентная среда отсутствует

. Турбулентная <Ереда \- ., ж. присутствует. '

Алгоритм

обработки

отсчетов ОПК

ЭВМ

Результаты измерений

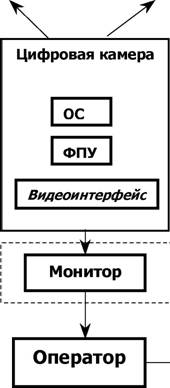
Рис. 2.1. Блок-схема эксперимента

С помощью измерительной цифровой камеры проводится последовательная съемка резкого края в отсутствии турбулентности и с ней. Первая съемка осуществляется в равномерно прогретом, изолированном от внешних температурных градиентов помещении. Вторая - через анализируемую среду. И в том и в другом случае ориентация цифровой камеры должна обеспечивать малый угол ср.

Оператор проводит анализ полученных изображений с целью определения отсчетов ОПК. Полученные данные (отсчеты ОПК) вводятся в ЭВМ, где обрабатываются по алгоритму, представленному на рис.2.2.

Электронный журнал ИССЛЕДОВАНО В РОССИИаа 835

Исходный массив

' к

Результат медианной фильтрации

уРаствор апертуры- 27

Апертура фильтра

Результат низкочастотной фильтрации

Результат дифференцирования ОПК

Электронный журнал ИССЛЕДОВАНО В РОССИИа 836а

Относительные значения

сигнала в элементах

анализируемого столбц Обобщенная ПОГраНИЧНаЯ КрИВаЯ

Угол- 8.333083 град

Оптическая система - ОКС ( фокус 75 мм)

Шаг решетки - 4.65 мкм

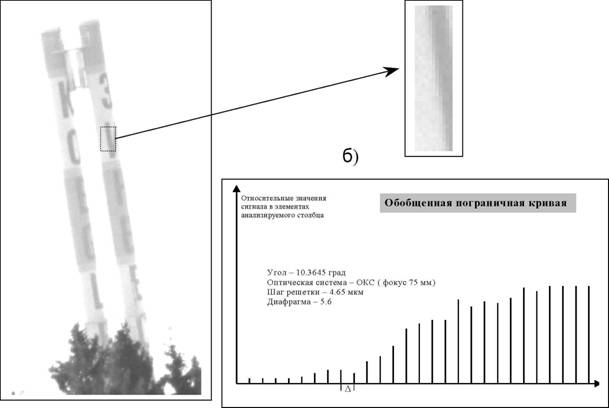
Диафрагма - 5.6

в)

Рис. 2.3. Изображение резкого края, полученное в помещении:

Съёмки через турбулентную атмосферу осуществлялись по слабонаклонной трассе. Объект наблюдения находился на расстоянии 1_=2,5 км. На рис. 2.3, 2.4 приведены примеры полученных экспериментальных данных.

Электронный журнал ИССЛЕДОВАНО В РОССИИа 837

а)

в)

Рис. 2.4. Одно из серии изображений резкого края, полученное через турбулентную среду: а)изображение, имеющее резкую границу смежных полей; б) анализируемый франмент изображения; в) отсчеты ОПК

В процессе эксперимента было получено двадцать аналогичных рис. 2.4.а изображений. Съёмка объекта осуществлялась через равные промежутки времени в течение 10 минут. Результаты, количественно отражающие уровень турбулентности атмосферы на момент съемки, сведены в гистограмму, представленную на рис.2.5.

Частота появления

Чi------------- 1----------- 1---------- 1----------- 1---------- 1----------- 1Ч>ж у гл. сек

8.0аа 11.0аа 14.0

Угловой размер раствора апертурной функции турбулентной "замороженной атмосферы"

Электронный журнал ИССЛЕДОВАНО В РОССИИаа 838 Все научные статьи

Blog

Сикорский Д.А. Метод оценки уровня турбулентности атмосферы