Авторефераты по темам >> Разные специальности - [часть 1] [часть 2]

АСИМПТОТИЧЕСКИЙ ВЕРОЯТНОСТНЫЙ ГЕНЕТИЧЕСКИЙ АЛГОРИТМ РЕШЕНИЯ СЛОЖНЫХ ЗАДАЧ ГЛОБАЛЬНОЙ ОПТИМИЗАЦИИ

Автореферат кандидатской диссертации

На правах рукописи

Галушин Павел Викторович

05.13.01 - Системный анализ, управление и обработка информации

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата технических наук

Красноярск - 2012

Работа выполнена в ФГБОУ ВПО Сибирский государственный аэрокосмический университет имени академика М.Ф. Решетнева (СибГАУ) г. Красноярск

Научный руководитель

доктор технических наук, профессор

Семёнкина Ольга Эрнестовна

Официальные оппоненты:

овчиков Анатолий Николаевич

доктор технических наук, профессор, Сибирский государственный аэрокосмический университет, институт Информатики и телекоммуникаций, профессор кафедры Информатики и вычислительной техники

Миркес Евгений Моисеевич

доктор технических наук, профессор, Сибирский федеральный университет, институт Космических и информационных технологий профессор кафедры вычислительной техники

Ведущая организация:

ФГБОУ ВПО Национальный исследовательский Томский политехнический университет

Защита состоится л 18аа амая 2012 г.а в аа14.00а ачасов

на заседании диссертационного совета Д 212.249.02 в ФГБОУ ВПО Сибирский государственный аэрокосмический университет имени академика М.Ф. Решетнева по адресу 660014 г. Красноярск, проспект имени газеты Красноярский рабочий, 31

С диссертацией можно ознакомиться в библиотеке Сибирского государственного аэрокосмического университета имени академика М.Ф. Решетнева

Автореферат разослан лаа апреля 2012 г.а

Ученый секретарь диссертационного совета аа А. А. Кузнецов

доктор физико-математических наук

Общая характеристика работы

Актуальность. Задачи оптимизации постоянно возникают в деятельности человека, в частности, при проектировании технических и социально-экономических систем: если существует возможность выбора параметров такой системы, то их следует выбрать оптимальным с точки зрения цели функционирования системы образом. Классические методы оптимизации накладывают существенные ограничения на целевую функцию задачи оптимизации: выпуклость, аналитическое задание функции и возможность вычисления вектора градиента в любой допустимой точке. Однако многие возникающие задачи оптимизации не укладываются в эти рамки. Развитие техники и производства привело к появлению задач оптимизации,а характеризующихся такими свойствами как алгоритмическое задание целевой функции, наличие большого количества локальных экстремумов, большая размерность и различный характер параметров (задача может одновременно иметь двоичные, целочисленные и вещественные параметры).

Важным классом методов оптимизации, способных решать такие задачи оптимизации являются эволюционные алгоритмы и, в частности, генетические алгоритмы (ГА), основанные на имитации эволюционных процессов, происходящих в природе. Дальнейшим развитием данного направления стали алгоритмы оптимизации с оценкой распределения и вероятностный генетический алгоритм (ВГА), основная идея которых заключается в интерпретации эволюционных процессов, лежащих в основе ГА, с точки зрения теории вероятностей и математической статистики. В методах этого класса вместо генетического оператора скрещивания используется процедура оценивания распределения вероятностей значений переменных и порождения решений с заданным распределением.

Однако существующие эволюционные методы оптимизации имеют большое количество настраиваемых параметров, что затрудняет их использование специалистами в прикладных областях, не являющимися экспертами в эволюционных методах оптимизации. Ситуацию ещё более усугубляет использование биологической терминологии при описании эволюционных алгоритмов. Кроме того, многие эволюционные алгоритмы (в частности, генетический алгоритм) определены так, что их программные реализации оказываются плохо приспособленными для современных ЭВМ (с конвейерной архитектурой и аппаратной многопоточностью).

Таким образом, разработка и исследование эволюционных алгоритмов, имеющих меньшее число настраиваемых параметров, имеющих ясную интерпретацию в терминах теории вероятности и эффективно использующих особенности архитектуры ЭВМ, является актуальной научно-технической задачей.

Целью работы является повышение эффективности решения сложных задач оптимизации эволюционными алгоритмами. Для достижения поставленной цели необходимо решить следующие задачи:

Выполнить обзор существующих методов глобальной оптимизации.
Разработать модификации существующих эволюционных алгоритмов, превосходящие существующие по быстродействию и эффективности.
Реализовать предложенные методы в виде программных систем.
Применить разработанные методы для решения практических задач оптимизации и сравнить с существующими методами по критериям эффективности и быстродействия.

Методы исследования. При выполнении диссертационной работы использовались методы теории оптимизации, теории вероятностей и математической статистики, системного анализа и исследования операций, теории эволюционных алгоритмов, дифференциального и интегрального исчисления, дискретной математики, методика создания прикладных интеллектуальных систем.

Научная новизна результатов диссертационной работы состоит в следующем:

Предложен новый асимптотический вероятностный генетический алгоритм (АВГА) псевдо-булевой оптимизации, превосходящий известные аналоги (ГА, ВГА и другие) по быстродействию и эффективности использования аппаратных средств ЭВМ, но не уступающий им по надёжности решения задач оптимизации.
Предложен новый способ учёта взаимосвязи между переменными, позволяющий повысить эффективность ВГА и АВГА.
Предложены модификации ГА, ВГА и АВГА, позволяющие эффективно решать задачи оптимизации с целочисленными переменными.
Предложена модификация рыночного алгоритма динамического составления расписаний, основанная на идее регуляризации функции предложения и позволяющая уменьшить время выполнения работ.

Теоретическая значимость результатов диссертационного исследования состоит в том, что разработаны, исследованы и апробированы новые эволюционные алгоритмы глобальной оптимизации, превосходящие существующие аналоги по эффективности и быстродействию.

Практическая значимость. Разработанные в ходе исследования алгоритмы реализованы в виде программ Асимптотический вероятностный генетический алгоритм (APGA) и Глобальная оптимизация локальными и эволюционными мультиагентными стохастическими алгоритмами (GOLEM-SA), зарегистрированных в Роспатенте (№2012612374, №2011611158). Данные программные системы позволяют пользователям, не являющимся экспертами в эволюционной оптимизации, эффективно решать сложные практические задачи глобальной оптимизации. Они прошли апробацию на ряде практических задач и продемонстрировали превосходство над существующими аналогами по надёжности и быстродействию.

Реализация результатов работы. Результаты работы вошли в отчёты по НИР № 2.1.1./2710 Математическое моделирование инвестиционного развития региональных экономических систем АВЦП Развитие научного потенциала высшей школы (2009Ц2010 годы), НК-136П/3 Автоматизированная система решения сложных задач глобальной оптимизации многоагентными стохастическими алгоритмами по направлению Обработка, хранение, передача и защита информации в рамках мероприятия 1.2.2 и НК-409П/49 Разработка устойчивого гибридного генетического алгоритма для определения кристаллических структур химических соединений из данных порошковой дифракции по направлению Физические методы исследования химических соединений в рамках мероприятия 1.2.1 Федеральной целевой программы Научные и научно-педагогические кадры инновационной России на 2009Ц2013 годы. В 2011 году по результатам исследования диссертанту присуждена Государственная премия Красноярского края в области системного анализа.

Основные защищаемые положения:

Асимптотический вероятностный генетический алгоритм (АВГА) псевдо-булевой оптимизации превосходит наиболее часто используемые эволюционные алгоритмы оптимизации по эффективности, быстродействию и затратам памяти.
Модификации ВГА и АВГА, предназначенные для решения задач дискретной оптимизации, превосходят по эффективности свои аналоги, использующие бинарное кодирование решений.
Учёт взаимосвязи переменных задачи оптимизации в ВГА и АВГА позволяет повысить эффективность этих алгоритмов.
АВГА позволяет эффективно решать задачу настройки параметров рыночного алгоритма динамического составления расписания.
Регуляризация функции предложения позволяет повысить эффективность рыночного алгоритма динамического составления расписаний.

Публикации. По теме диссертации опубликовано тринадцать работ, в том числе пять в изданиях из перечня ВАК.

Апробация результатов работы. Результаты работы были представлены на Всероссийской научно-практической конференции Актуальные проблемы авиации и космонавтики, Международных научно-практических конференциях Решетневские чтения (Красноярск, СибГАУ, 2005, 2006, 2009), на 11-й Международной конференции Natural Computations в Шанхае (КНР, 2011), на Международных конференциях Distributed Computing and Artificial Intelligence и Hybrid Artificial Intelligence Systems в Саламанке (Испания, 2012).

Структура работы. Диссертация состоит из введения, четырёх глав, заключения, списка литературы.

Основное содержание работы

Во введении обоснована актуальность работы, сформулирована цель и поставлены задачи исследования, рассмотрены вопросы научной новизны и практической ценности проведенных исследований, изложены основные положения, выносимые на защиту.

В первой главе даётся обзор существующих методов глобальной оптимизации: мультистарт локального поиска, метод группировок, топографический метод, методы покрытий и метод интервалов, метод туннелей, метод сглаживания целевой функции, методы оптимизации, основанные на непараметрической оценке кривой регрессии, метод усреднения координат, метод направляющего конуса, метод имитации отжига, поведенческие алгоритмы оптимизации, матричный алгоритм глобального поиска, эволюционные стратегии (ЭС), стайные алгоритмы (PSO), методы дифференциальной эволюции, муравьиные алгоритмы, алгоритм пчелиной колонии, генетический алгоритм (ГА) и алгоритм GENITOR, квантовые эволюционные алгоритмы, алгоритмы с оценкой распределения (EDA) и вероятностный генетический алгоритм (ВГА).

Вводятся обозначения, используемые в тексте диссертации. Пусть N Ч размер популяции, f Ч целевая функция, r Ч вероятность мутации. Исходная популяция состоит из булевых векторов U1,...,UN размерности M: Uk={uk1,...,ukM}. В результате селекции выбираются Nа векторов X1,...,XN размерности M: Xk={xk1,...,xkM}, P={p1,...,pM} Ч вектор средних арифметических компонент решений, отобранных в ходе селекции:

Результат действия оператора мутации на вектор Xk будем обозначать X'k. Вектора X'k является случайными, так как мутация Ч стохастическая процедура. Вектор средних для векторов X'k обозначим P'={p'1,..., p'M}:

а.а (1)

Далее в первой главе на основе анализа теоретико-вероятностных свойств вероятностного генетического алгоритма, предлагается новый алгоритм оптимизации Ч асимптотический вероятностный генетический алгоритм.

Работу ВГА можно описать следующим образом:

Распределение значений генов в начале работы Ч равномерное, положить pi<1/2, i=1ЕM.
Создать популяциюU1,Е,UN, в которой компоненты каждого вектораUk являются независимыми случайными булевыми величинами, причём P{uki=1}=pi.
Вычислить значения целевой функции yk=f(Uk).
Если выполнен критерий останова Ч прекращаем работу.
Сформировать промежуточную популяцию X1,...,XN с помощью выбранного метода селекции.
Применить к полученным решениям оператор мутации, мутировавшие решения обозначим X'1,Е, X'N.
Вычислить p'i, i=1ЕM , по формуле (1).
Положить pi=p'i,i=1ЕM.
аПерейти к шагу 2.

Теорема. Имеют место равенства

Следствие. Дисперсия вектора средних мутировавших векторов стремится к нулю при размере популяции, стремящемся к бесконечности:

Таким образом, при больших размерах популяции отклонения компонент вектора средних от их математических ожиданий стремится к нулю. Используя вместо P' его математическое ожидание, получим процедуру мутации, статистически эквивалентную традиционной мутации ВГА, но требующую меньше вычислений:

Данную процедуру можно назвать асимптотической мутацией, так как она, фактически, является предельным эквивалентом традиционного оператора мутации при размере промежуточной популяции, стремящемся к бесконечности.

Устанавливаются следующие свойства предложенной процедуры:

Преобразование (1) является линейным и сжимает отрезок [0;1]а до отрезка [r;1-r].
Значение p=0,5 является неподвижной точкой отображения (1).
Время выполнения асимптотической мутации не зависит от размера популяции.
Программная реализация асимптотической мутации не содержит условных инструкций.
Программная реализация асимптотической мутации не требует генерации псевдослучайных чисел.

Проведём аналогичный анализ для оператора селекции. Будем считать теперь векторы-решения U1,...,UN случайными, каждому из которых назначена вероятность прохождения отбора (в одном испытании): g1,...,gN. Подсчитаем математическое ожидание вероятности того, что i-й ген окажется равным единице.

Теорема. Имеет место равенство

Теорема. Имеет место неравенство:

Следствие.

Так как дисперсия pi стремится к нулю, мы можем использовать вместо случайных значений pi их математические ожидания.

Предложенный оператор можно назвать асимптотической селекцией. В обычных операторах пропорциональной и ранговой селекции вероятности прохождения отбора g1,...,gN вычисляются явно, поэтому они могут быть использованы как реализации асимптотической селекции непосредственно. Алгоритм оптимизации, аналогичный ВГА, но использующий асимптотические мутацию и селекцию, назван асимптотическим вероятностным генетическим алгоритмом (АВГА). Работу АВГА можно описать следующим образом:

Распределение значений генов в начале работы Ч равномерное, положить pi<1/2, i=1ЕM.
Создать популяциюU1,Е,UN, в которой компоненты каждого вектораUk являются независимыми случайными булевыми величинами, причём P{uki=1}=pi.
Вычислить значения целевой функции аyk=f(Uk).
Если выполнен критерий останова Ч прекращаем работу.
Вычислить вероятности прохождения отбора g1,...,gN.
Вычислить величины .
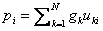Применить к полученному распределению оператор асимптотической мутации
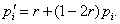
Положить pi=p'i,i=1ЕM.
Перейти к шагу 2.

Во второй главе АВГА обобщается в следующих направлениях: добавляется турнирная селекция, рассматривается целочисленное представление решений и вводится учёт корреляций между переменными.

В процедуре турнирной селекции вероятности отбора в явном виде не вычисляются. Однако турнирная селекция во многих случаях оказывается более надёжной и эффективной, чем другие методы, поэтому распространение асимптотического подхода на этот метод селекции является важной задачей. Пусть в популяции N решений, которым соответствуют значения целевой функции y1,...,yN. Вычислим вероятности g1,...,gN отбора решений при турнирной селекции (размер турнирной группы обозначим как t). Сначала получим вероятности выбора для значений целевой функции, а не для решений. Пусть в популяции встречается K различных значений пригодности: Y1,...,YK, причём k-е значение (то есть Yk) встречается nk раз. Сумма всех nk аравна N

Будем также предполагать, что значения Yk упорядочены по возрастанию. Вероятность выбора значения Yk обозначим как bk. Рассмотрим величины

По определению, Bk Ч это вероятность того, что будет выбрано решение со значением целевой функции, меньшим либо равным Yk. Так как отбор в турнирную группу осуществляется случайным образом, причём все особи имеют равный шанс прохождения в турнирную группу, то данная вероятность равна отношению количества турнирных групп, содержащих только значения, меньшие либо равные Yk, к общему количеству турнирных групп. Обозначим число турнирных групп размера t для m особей как s(m,t), отметим, что это число зависит от способа формирования промежуточной популяции, и введём частичные суммы

Будет иметь место следующее равенство:

Теперь можно вычислить обычные вероятности выбора для значений:

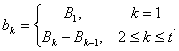
Так как значение Yk встречается в коллективе решений nk раз, и все решения с одинаковым значением целевой функции должны иметь одинаковую вероятность выбора, то вероятность выбора для решения со значением целевой функции Yk равна bk/nk. Выражение вероятности выбора особи через вероятности выбора значений можно записать следующим образом:

Наконец, необходимо получить выражение для функции s(k,t), которая определяет количество турнирных групп. Если отбор в турнирную группу производится с повторами, то данная функция имеет простой вид:

В случае отбора без повторов, формула получается более сложной:

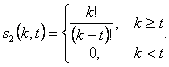
Оценивается величина разности между значениями вероятностей, получаемых по формулам для выборки с повторами и без повторов:

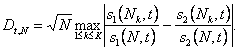
Доказана следующая теорема:

Теорема. Если t Ч постоянная величина, то

Далееа обосновывается асимптотический вероятностный генетический алгоритм для более общего случая целочисленных (не бинарных) переменных. Пусть i-я компонента векторов Xk может принимать целочисленные значения из интервала [0;li-1]. Введём следующее обозначение для вероятностей различных значений: pij Ч вероятность того, что i-я компонента вектора примет значение j. Вероятности значений компонент решений после мутации обозначим .

Обсуждается адаптация обычных операторов скрещивания и мутации к случаю дискретных переменных, обосновывается применение асимптотической мутации.

Теорема. Имеют место следующие равенства:

Как и для случая бинарных переменных, было доказано, что асимптотическая мутация преобразует распределение компонент векторов решений в более близкое к равномерному.

Теорема. Распределение вероятностей аближе к равномерному распределению, чем :

В результате получен АВГА с целочисленным типом хромосом, аналогичный ранее исследованному бинарному АВГА.

Далее рассматривается учёт корреляций между переменными в АВГА. Входными данными для процедуры синтеза генератора случайных векторов является ковариационная матрица C с компонентами

и одномерные распределения генов, которые определяются величинами pij.

Вычислим элементы корреляционной матрицы:

Далее, тем элементам корреляционной матрицы, которые статистически незначимо отличаются от нуля, присваивается нулевое значение. Преобразованную таким образом корреляционную матрицу представляют (с помощью разложения Холецкого) в виде произведения R=STS , где S Ч верхне-диагональная матрица.

Наконец, рассчитываются пороговые значения для преобразования стандартного нормального распределения в дискретные распределения отдельных генов:

где Фinv Ч обратная функция распределения стандартного нормального распределения. Процедура генерации случайных величин с заданной ковариационной матрицей выглядит следующим образом:

Порождаем M независимых стандартных нормальных случайных величин zi, составляющие случайный вектор Z={z1,...,zM}
Вычисляем вектор случайных величин Y=SZ с заданной корреляционной матрицей.
Элементы вектора Y преобразуются в значение генов с помощью дискретизации: xi=j: ti(j-1)<yi<tij, i=1...M.

Чтобы учитывать взаимосвязи переменных в АВГА, необходимо установить, как ковариационная матрица меняется при мутации. Пусть Xk Ч одинаково распределённые случайные булевы векторы с компонентами {xk1,Е,xkM}, причём M[xki]=pi и Cov(xki,xkj)=cij. Значение ковариации после мутации обозначим как .

Теорема. Если все переменные Ч бинарные, то

Теорема. Если , то имеет место равенство

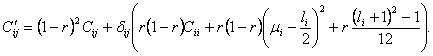
Роль мутации с точки зрения теории численных методов заключается в том, число обусловленности матрицы аменьше, чем у матрицы C.

Таким образом, разложение Холецкого для мутировавшей корреляционной матрицы имеет меньшую вычислительную погрешность, чем для исходной матрицы.

В третьей главе описывается программная реализация предложенных алгоритмов и их исследование на тестовых задачах оптимизации.

Программная система Асимптотический вероятностный генетический алгоритм (APGA) разработана на языке программирования C++ с использованием методологии мультипарадигменного проектирования. Программная система предназначена для решения задач условной и безусловной оптимизации с дискретными и вещественными переменными. В отличие от многих аналогичных программ, целевые функции и функции, задающие ограничения, не выбираются из фиксированного списка, а импортируются из подготовленных специальным образом динамически загружаемых библиотек (.dll в операционных системах семейства Microsoft Windows и .so Ч в операционных системах семейства GNU/Linux). Такой подход требует определённых навыков программирования от пользователя, но существенно расширяет возможности системы: значения целевой функции могут вычисляться по сколь угодно сложному алгоритму с использованием любых библиотек на языке С++, что принципиально невозможно при использовании интерпретатора или фиксированного набора функций.

В программной системе Асимптотический вероятностный генетический алгоритм (APGA) реализованы следующие методы оптимизации: стандартный генетический алгоритм (ГА), вероятностный генетический алгоритм (ВГА) и асимптотический вероятностный генетический алгоритм (АВГА). Для каждого алгоритма существует возможность выбора максимального основания системы счисления для кодирования небинарных переменных (от 2 до 32). Для ВГА и АВГА реализованы версии, учитывающие взаимосвязи между переменными.

Программная система Глобальная оптимизация локальными и эволюционными мультиагентными стохастическими алгоритмами (GOLEM-SA), как и предыдущая, предназначена для решения сложных задач оптимизации, но в ней делается упор на автоматизацию выбора наиболее подходящего алгоритма оптимизации для данной задачи оптимизации, что позволяет решать сложные задачи оптимизации специалистам предметных областей, не являющимися экспертами в области эволюционных методов оптимизации. В данной программной системе реализованы следующие методы оптимизации: мультистарт локального поиска, стандартный генетический алгоритм (ГА), вероятностный генетический алгоритм (ВГА) и асимптотический вероятностный генетический алгоритм (АВГА), метод последовательного популяционного обучения (PBIL), роевые алгоритмы вещественной, дискретной, псевдо-булевой и смешанной оптимизации (PSO, Particle Swarm Optimization), а также коэволюционный алгоритм, сочетающий преимущества эволюционных и роевых алгоритмов.

В таблице 1 приведены результаты сравнения на тестовых задачах без шума из набора Black-Box Optimization Benchmarking (BBOB) 2010 ГА и методов, не учитывающих корреляции между распределениями: PBIL, АВГА и ВГА. В таблицах 1-3 delta обозначает разность между лучшим значением целевой функции, достигнутым алгоритмом, и значением целевой функции в глобальном оптимуме, а p Ч это доля запусков, в которых такая разность была достигнута. Лучшим считался алгоритм с меньшей delta, при равных значениях delta, лучше алгоритм с большим значением p. В таблице 1 полужирным выделены лучшие значения в строке.

Таблица 1. Сравнение методов оптимизации, не учитывающих корреляции.

Алгоритм	ГА		ВГА		АВГА		PBIL
Задача	delta	p	delta	p	delta	p	delta	p
F1	1e-6	0,91	1e-6	0,99	1e-6	1	1e-6	1
F2	0,01	0,68	0,01	0,96	0,01	1	0,1	1
F3	1e-5	0,28	1e-5	0,49	1e-5	0,91	1e-3	0,98
F4	1e-3	0,3	1e-3	0,52	1e-3	0,98	1e-3	1
F5	0	0,42	0	0,81	0	1	0	1
F6	1e-4	0,12	1e-4	0,09	1e-5	1	1e-5	1
F7	1e-6	0,98	1e-8	1	1e-9	1	1e-9	0,18
F8	1e-6	0,11	1e-6	0,04	1e-6	0,12	1e-5	0,17
F9	1e-4	0,11	1e-4	0,04	1e-4	0,22	1e-4	0,36
F10	0,1	0,15	0,1	0,09	0,1	0,15	0,1	0,05
F11	0,1	0,12	0,1	0,12	0,1	0,1	0,1	0,04
F12	0,01	0,08	0,01	0,12	0,01	0,1	0,01	0,03
F13	1e-3	0,09	1e-3	0,08	1e-4	0,12	1e-5	0,09
F14	1e-4	0,12	1e-5	0,13	1e-5	0,13	1e-4	0,32
F15	1e-4	0,08	1e-4	0,1	1e-4	0,73	1e-4	0,62
F16	1e-3	0,24	1e-3	0,58	1e-3	0,97	1e-3	0,67
F17	1e-3	0,14	1e-3	0,37	1e-3	0,93	0,01	0,92
F18	0,1	0,18	0,1	0,24	0,1	0,61	0,1	0,17
F19	1	1,00	0,1	0,06	0,1	0,08	0,1	0,27
F20	0,1	0,54	0,1	0,41	0,1	0,80	0,1	0,27
F21	0,1	0,52	0,1	0,67	0,1	0,53	0,1	0,60
F22	0,1	0,13	0,1	0,40	0,1	0,27	0,1	0,67
F23	1	0,98	1	0,61	0,1	0,87	1	0,93
F24	10	1,00	10	0,86	10	1,00	1	0,67
Победы	1		3		15		9

Из таблицы видно, что АВГА превосходит ГА и ВГА практически на всех задачах по точности и надёжности нахождения решения. Кроме того, АВГА обладает большим быстродействием (на 30-50% быстрее, в зависимости от задачи). АВГА также превосходит другой широко известный метод класса EDA, не учитывающий взаимосвязи между переменными Ч PBIL.

Необходимо выяснить, как влияет учёт зависимостей между переменными на эффективность алгоритмов оптимизации. В таблице 2 приведены результаты решения задач оптимизации из пакета BBOB методами оптимизации, учитывающими корреляции между переменными (BOA - байесовский алгоритм оптимизации). Строка Улучшения содержит количество целевых функций, на которых алгоритм с учётом зависимостей между переменными превосходит аналогичный алгоритм без учёта зависимостей. В таблице 2 полужирным выделены случаи, когда учёт корреляций приводит к повышению эффективности решения задачи оптимизации.

Таблица 2. Сравнение методов оптимизации, учитывающих корреляции.

	ВГА		ВГА-2		АВГА		АВГА-2		BOA
Функция	delta	p	delta	p	delta	p	delta	p	delta	p
F1	1e-6	0,99	1e-13	1,00	1e-6	1	1e-8	1	1e-6	0,41
F2	0,01	0,96	1	0,05	0,01	1	0,01	1	0,1	0,69
F3	1e-5	0,49	1e-30	0,89	1e-5	0,91	1e-5	0,98	1e-3	0,25
F4	1e-3	0,52	0,1	0,01	1e-3	0,98	1-3	0,98	1e-3	0,3
F5	0	0,81	0,01	0,01	0	1	0	1	0	0,38
F6	1e-4	0,09	1e-3	0,03	1e-5	1	1e-5	1	1e-4	0,04
F7	1e-8	1	1e-7	0,99	1e-9	1	1e-9	1	1e-6	0,14
F8	1e-6	0,04	1e-6	0,42	1e-6	0,12	1e-6	0,19	1e-3	0,09
F9	1e-4	0,04	1e-7	0,48	1e-4	0,22	1e-4	0,27	1e-3	0,03
F10	0,1	0,09	1e-7	0,82	0,1	0,15	1e-3	0,03	0,1	0,11
F11	0,1	0,12	1e-5	0,16	0,1	0,1	0,1	0,11	0,1	0,06
F12	0,01	0,12	1e-5	0,2	0,01	0,1	1e-4	0,04	0,01	0,01
F13	1e-3	0,08	1e-6	0,96	1e-4	0,12	1e-4	0,18	1e-3	0,02
F14	1e-5	0,13	1e-9	0,33	1e-5	0,13	1e-4	0,03	1e-4	0,11
F15	1e-4	0,1	1e-4	0,01	1e-4	0,73	1e-4	0,69	1e-4	0,03
F16	1e-3	0,58	1e-3	0,05	1e-3	0,97	1e-3	0,13	1e-3	0,26
F17	1e-3	0,37	1e-3	0,32	1e-3	0,93	1e-3	0,83	1e-2	0,31
F18	0,1	0,24	0,01	0,74	0,1	0,61	0,1	0,32	0,1	0,01
Улучшения			10				7

Из таблицы 2 видно, что учёт корреляций повышает эффективность ВГА для 10 целевых функций. В случае АВГА учёт корреляций повышает эффективность нахождения оптимума для 7 целевых функций, для ещё 4 задач различий нет.

Кроме того, ВГА и АВГА с учётом корреляций превосходят наиболее распространённый метод класса EDA с учётом зависимостей переменных Ч BOA. Отметим, что BOA обладает существенно меньшим быстродействием, чем АВГА: примерно в 15-30 раз в зависимости от целевой функции.

Так как в некоторых случаях учёт взаимосвязи переменных приводит к ухудшению эффективности алгоритмов оптимизации, то необходимо реализовать гибридную схему, позволяющую избегать худших случаев. Простейшим вариантом, является схема, аналогичная используемой в классических методах оптимизации: в начале процесса оптимизации используются методы первого порядка (в нашем случае Ч без учёта взаимосвязей переменных), а после нахождения хорошего приближения Ч методы второго порядка (методы с учётом взаимосвязей между переменными).

В таблице 3 приведены результаты сравнения гибридной схемы с худшим результатов аналогичных алгоритмов без учёта корреляций и учётом корреляций на всех итерациях, (А)ВГА-1-2 Ч это модификация (А)ВГА, в котором на первой половине итераций взаимосвязи переменных не учитываются, а на второй Ч учитываются. Полужирным выделены результаты, когда гибридная схема позволяет избежать худшего случая.

Таблица 3. Эффективность гибридного метода.

	Худшее из ВГА иа ВГА-2		ВГА-1-2		Худшее из АВГА и АВГА-2		АВГА-1-2
Функция	delta	p	delta	p	delta	p	delta	p
F1	1e-6	0,99	1e-11	1,00	1e-6	1,00	1e-16	1,00
F2	1	0,05	0,01	0,99	0,01	1,00	0,01	1,00
F3	1e-5	0,49	1e-5	0,51	1e-5	0,91	1e-5	1,00
F4	0,1	0,01	1e-3	0,59	1e-3	0,98	1e-3	1,00
F5	0,01	0,01	0	0,85	0	1,00	0	1,00
F6	1e-3	0,03	1e-4	0,11	1e-5	1,00	1e-5	1,00
F7	1e-7	0,99	1e-9	0,12	1e-9	1,00	1e-9	0,09
F8	1e-6	0,04	1e-4	0,06	1e-6	0,12	1e-5	0,04
F9	1e-4	0,04	1e-4	0,08	1e-4	0,22	1e-4	0,12
F10	0,1	0,09	0,1	0,12	0,1	0,15	0,1	0,22
F11	0,1	0,12	0,1	0,20	0,1	0,1	0,1	0,29
F12	0,01	0,12	0,01а	0,12	0,01	0,1	0,01	0,17
F13	1e-3	0,08	1e-3	0,24	1e-4	0,12	1e-4	0,08
F14	1e-5	0,13	1e-5	0,08	1e-4	0,03	1e-4	0,46
F15	1e-4	0,01	1e-4	0,11	1e-4	0,69	1e-4	0,59
F16	1e-3	0,58	1e-3	0,67	1e-3	0,13	1e-3	0,93
F17	1e-3	0,37	1e-3	0,42	1e-3	0,83	1e-3	0,89
F18	0,1	0,24	0,1	0,27	0,1	0,32	0,1	0,42

Как видно из приведённых результатов, практически во всех случаях использование гибридного алгоритма позволяет избежать худшего случая, что повышает вероятность успешного решения задачи оптимизации специалистами предметных областей, не являющихся экспертами в области эволюционной оптимизации.

В четвёртой главе предложенные алгоритмы оптимизации применяются для решения практической задачи динамического составления расписаний.

На вход системы обслуживания поступает поток заявок на выполнение работ, характеризующихся типом. Для выполнения заявок существует несколько однотипных процессоров. На выполнение работы процессору требуется определенное время. Кроме того, если тип выполненной и новой работы не совпадают, то процессор требует переналадки, которая также занимает определенное время. Процессоры выходят из строя случайным образом. Время ремонта является случайной величиной. Задача состоит в распределении работ по процессорам таким образом, чтобы минимизировать время выполнения всех работ. Переналадка процессоров увеличивает время выполнения работ и может требовать больших расходов, поэтому количество переналадок должно быть уменьшено.

Так как характеристики и время появления задач не известны заранее, то планирование в классическом смысле невозможно. Необходимо использовать некоторую эвристику. Примерами таких эвристик являются рыночный и муравьиный алгоритмы. Эти алгоритмы имеют параметры, которые могут быть настроены с помощью методов оптимизации, способных работать в случае алгоритмически заданной целевой функции. Анализ рыночного алгоритма показал, что его эффективность может быть повышена за счёт регуляризации так называемой функции предложения Ч она не должна обращаться в бесконечность.

Рыночный алгоритм динамического составления расписания был применён для управления участком окраски грузовых автомобилей. Работы характеризуются цветом, в который должен быть окрашен грузовик. Время окрашивания не зависит от цвета (3 минуты), но если поступающий в камеру окрашивания грузовик должен быть окрашен не в тот же цвет, что предыдущий, то необходимо сменить краску, что также занимает 3 минуты (кроме того, смена краски является затратной). Целью является минимизация общего времени выполнения всех работ. В таблице 4 приведены результаты решения задачи выбора параметров рыночного алгоритма для управления участком окраски грузовиков различными эволюционными алгоритмами (ВГА-2 Ч ВГА с учётом корреляций, АВГА-2 Ч АВГА с учётом корреляций). Полужирным выделены лучшие результаты.

Из таблицы видно, что лучшее значение целевой функции достигнуто гибридной схемой АВГА (первая половина итераций Ч без учёта корреляций, вторая половина Ч с учётом корреляций). При этом использование десятичного кодирования повышает эффективность по сравнению с двоичным кодированием.

Таблица 4. Результаты решения задачи выбора параметров рыночного алгоритма

Алгоритм	Среднее	Ср. кв. уклонение	Затраченное время (секунды)
ГА (двоичный)	4,62	0,89	9,85
ГА (десятичный)	4,69	0,87	9,31
ВГА (двоичный)	4,70	0,74	10,60
ВГА (десятичный)	4,86	0,94	9,99
АВГА (двоичный)	4,65	0,89	9,26
АВГА (десятичный)	4,68	0,66	9,81
ВГА-2 (двоичный)	4,73	0,83	10,27
ВГА-2 (десятичный)	4,90	1,02	9,82
АВГА-2 (двоичный)	4,72	0,78	10,12
АВГА-2 (десятичный)	4,24	0,69	9,11
ВГА-1-2 (двоичный)	3,83	0,63	9,83
ВГА-1-2 (десятичный)	3,74	0,48	10,18
АВГА-1-2 (двоичный)	3,92	0,61	10,22
АВГА-1-2 (десятичный)	3,65	0,61	9,55
PBIL	4,32	0,64	10,28
BOA	3,62	0,57	23,67

Аналогично, гибридный ВГА превосходит как стандартный ВГА, так и ВГА с учётом корреляций. Гибридный АВГА превосходит широко распространённый метод класса EDA без учёта корреляций Ч PBIL, и имеет сравнимую эффективность с методом BOA (отметим, что BOA обладает существенно меньшим быстродействием, в данной задаче Ч более чем в два раза). АВГА превосходит другие методы эволюционной оптимизации без учёта зависимостей между переменными по быстродействию. АВГА с учётом корреляций превосходит по быстродействию другие методы оптимизации с учётом взаимосвязей между переменными (в том числе, BOA).

Далее рассматривается задача настройки параметров рыночного алгоритма для управления GRID-системой, то есть вычислительной сетью, состоящей из пространственно распределённых вычислительных ресурсов. Был рассмотрен следующий сценарий: задачи, которые должны быть решены с помощью GRID-системы, неизвестны заранее, то есть моменты их появления представляют собой поток случайных событий, а вычислительная сложность и объём задач являются случайными величинами. В качестве критерия качества использовалось среднее время завершения задач (с учётом времени, затраченного на пересылку данных) в секундах. Результаты численных экспериментов приведены в таблице 5.

Приведённые результаты показывают, что лучшее значение целевой функции было достигнуто гибридным АВГА.

Таблица 5. Результаты решения задачи управления GRID-системой

Алгоритм	Среднее	Ср. кв. уклонение	Затраченное время (секунды)
ГА (двоичный)	21,01	0,58	56
ГА (десятичный)	20,91	1,15	54
ВГА (двоичный)	20,61	1,27	55
ВГА (десятичный)	20,52	1,11	55
АВГА (двоичный)	20,86	1,22	57
АВГА (десятичный)	20,87	1,27	54
ВГА-2 (двоичный)	20,42	1,52	63
ВГА-2 (десятичный)	20,37	1,45	60
АВГА-2 (двоичный)	20,49	1,23	67
АВГА-2 (десятичный)	20,50	1,29	57
ВГА-1-2 (двоичный)	20,31	1,25	61
ВГА-1-2 (десятичный)	20,29	1,27	57
АВГА-1-2 (двоичный)	20,26	1,17	63
АВГА-1-2 (десятичный)	20,26	1,16	60
PBIL	20,39	1,27	54
BOA	20,27	1,24	74

Гибридный АВГА превосходит два широко известных метода класса EDA: PBIL (лучшее среднее значение целевой функции) и BOA (при примерно одинаковом среднем значении целевой функции, у гибридного АВГА меньше дисперсия и выше быстродействие). Быстродействие алгоритмов одного класса различается несущественно из-за того, что преобладающим фактором является время вычисления значения целевой функции, а не время проработки алгоритмов.

В заключение диссертации приведены основные результаты, полученные в ходе выполнения исследования, и сформулированы выводы.

Основные результаты и выводы

При проведении диссертационного исследования получены следующие результаты:

Предложен новый асимптотический вероятностный генетический алгоритм, превосходящий вероятностный генетический алгоритм по быстродействию и надёжности решения задач оптимизации.
Предложены модификации ВГА и АВГА, в которых учитываются корреляции между переменными задачи оптимизации.
Предложены модификации генетического алгоритма, ВГА и АВГА с небинарным кодированием переменных.
Разработаны, апробированы и зарегистрированы программные системы, реализующие предложенные алгоритмы оптимизации и позволяющие решать сложные задачи оптимизации специалистам предметных областей, не являющимся экспертами в эволюционных методах оптимизации.
Проведён сравнительный анализ существующих и предложенных алгоритмов при решении стандартных тестовых задач оптимизации и сложной практической задачи оптимизации: задачи настройки параметров эвристических алгоритмов динамического составления расписания (для управления цехом окраски автомобилей и управления GRID-системой).

Таким образом, в ходе диссертационного исследования были разработаны, реализованы, исследованы и апробированы новые эволюционные методы решения задач оптимизации, превосходящие аналоги по эффективности и быстродействию, что имеет существенное значение для теории и практики эволюционных методов оптимизации.

Публикации по теме диссертации

Галушин, П.В. Разработка и исследование асимптотического вероятностного генетического алгоритма / П.В. Галушин, О.Э. Семёнкина // Journal of Siberian Federal University. Mathematics & Physics. № 5(1). Ч 2011. Ч p. 46Ц56.
Галушин, П.В. Асимптотический вероятностный генетический алгоритм дискретной оптимизации // П.В. Галушин, О.Э. Семёнкина // Вестник Сибирского государственного аэрокосмического университета им. академика М.Ф. Решетнева. № 5 (38). Ч 2011. Ч С. 25-29.
Галушин, П.В. Автоматизированная система глобальной оптимизации многоагентными стохастическими алгоритмами / П.В. Галушин, С.Н. Ефимов, Е.С. Семёнкин, И.А. Панфилов // Программные продукты и системы. № 3 (95). Ч 2011. Ч С. 97-101.
Галушин, П.В. Асимптотический вероятностный генетический алгоритм / П.В. Галушин, Е.С. Семёнкин // Вестник Сибирского государственного аэрокосмического университета им. академика М.Ф. Решетнева. № 4 (25). Ч 2009. Ч С. 37-42.
Galushin, P.V. The asymptotic probabilistic genetic algorithm / P.V. Galushin, E.S. Semenkin // Вестник Сибирского государственного аэрокосмического университета им. академика М.Ф. Решетнева. № 5 (26). Ч 2009. Ч С. 45-49.
Galushin, P. Comparative Analysis of Two Distribution Building Optimization Algorithms / P. Galushin, O. Semenkina, A. Shabalov // In: Distributed Computing and Artificial Intelligence. Advances in Intelligent and Soft Computing, Volume 151. - 2012. - pp. 759-766.
Shabalov, A., Integration of Intelligent Information Technologies Ensembles for Modeling and>
Galushin, P.V. Design and analysis of asymptotic genetic algorithm / P.V. Galushin, O. E. Semenkina // Proc. of the 11th International Conference of Natural Computations. Ч 2011. Ч p. 1082-1087.
Shabalov, A. Automatized design application of intelligent information technologies for data mining problems / A. Shabalov, E. Semenkin, P. Galushin // Proc. of the 11th International Conference of Natural Computations. Ч 2011. Ч p. 2596-2599.
Галушин, П.В. Об асимптотическом вероятностном генетическом алгоритме / П.В. Галушин // Решетнёвские чтения: Материалы XIII Междунар. науч. конф., посвящ. 45-летию Сиб. гос. аэрокосмич. ун-та имени акад. М. Ф. Решетнева. (10-12 ноября 2009, г. Красноярск) / Под общ. ред. С. И. Сенашова. - Сиб. гос. аэрокосмич. ун-т. - Красноярск, 2009. - Ч. 2. - С. 409-411.
Галушин, П.В. Динамическое составление расписания адаптивными методами / П.В. Галушин // Вестник университетского комплекса: Сб. науч. трудов / Под общ. ред. профессора Н.В. Василенко. - Красноярск: ВСФ РГУИТП, НИИ СУВПТ. Ч 2006. Ч Выпуск 7 (21). Ч С. 111-115.
Галушин, П.В. Автоматизированная система решения сложных задач глобальной оптимизации многоагентными стохастическими алгоритмами (GOLEM-SA): свидетельство о государственной регистрации программы для ЭВМ / П.В. Галушин, С.С. Бежитский, и др. Ч М.: Реестр программ для ЭВМ, 2011. Номер гос. рег. №2011611158.
аГалушин, П.В. Асимптотический вероятностный генетический алгоритм (APGA): свидетельство о государственной регистрации программы для ЭВМ / П.В. Галушин Ч М.: Реестр программ для ЭВМ, 2012. Номер гос. рег. №2012612374.

Галушин Павел Викторович

Асимптотический вероятностный генетический алгоритм решения сложных задач глобальной оптимизации

Автореферат

Подписано к печати 16.04.2012. Формат 60х84/16

Уч. изд. л. 1.0 Тираж 100 экз. Заказ № ________

Отпечатано в отделе копировальной и множительной техники СибГАУ.

660014, г. Красноярск, пр. им. газ. Красноярский рабочий, 31

Авторефераты по темам >> Разные специальности - [часть 1] [часть 2]

Blog

АСИМПТОТИЧЕСКИЙ ВЕРОЯТНОСТНЫЙ ГЕНЕТИЧЕСКИЙ АЛГОРИТМ РЕШЕНИЯ СЛОЖНЫХ ЗАДАЧ ГЛОБАЛЬНОЙ ОПТИМИЗАЦИИ