Авторефераты по всем темам  >>  Авторефераты по экономике

Экономико-математические модели актуарной оценки страховых премий по данным из малых выборок при различных формах зависимости

Автореферат докторской диссертации по экономике

 

Санкт-Петербургский государственный университет

На правах рукописи

Кудрявцев Андрей Алексеевич

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ АКТУАРНОЙ

ОЦЕНКИ СТРАХОВЫХ ПРЕМИЙ ПО ДАННЫМ ИЗ

МАЛЫХ ВЫБОРОК ПРИ РАЗЛИЧНЫХ ФОРМАХ ЗАВИСИМОСТИ

Автореферат диссертации на соискание ученой степени доктора экономических наук

Специальность 08.00.13 - Математические и инструментальные методы

экономики

Санкт-Петербург 2011

Работа выполнена на кафедре управления рисками и страхования Экономического факультета Санкт-Петербургского государственного университета

Научный консультант: доктор экономических наук, профессор

Чернова Галина Васильевна Санкт-Петербургский государственный университет

Официальные оппоненты: доктор экономических наук, профессор

Дуболазов Виктор Андреевич Санкт-Петербургский государственный технический университет

доктор экономических наук, профессор Чернов Виктор Петрович Санкт-Петербургский государственный университет экономики и финансов

доктор экономических наук, профессор Емельянов Александр Анатольевич Московский финансово-промышленный

университет Синергия

Ведущая организация:а Московский государственный университет

им. М.В. Ломоносова

Защита состоится лаа 20 г. в часов

минут на заседании Совета Д 212.232.34 по защите докторских и кандидатнских диссертаций при Санкт-Петербургском государственном университенте по адресу: 191123, Санкт-Петербург, ул. Чайковского, 62, ауд. 415.

С диссертацией можно ознакомиться в Научной библиотеке им. A.M.

Горького Санкт-Петербургского государственного университета

Автореферат разослан л___ ___________ 20___ г.

Ученый секретарь Диссертационного совета

кандидат экономических наук, доцент \/ ~\ / , /> ВгЙ. Капусткин

I. ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность. Страхование - важная область финансовых операций и управления рисками, которая обеспечивает устойчивость работы всего нанродного хозяйства. В то же время эффективное функционирование страхованния во многом зависит от правильной оценки страховых премий, отражаюнщих принятые страховщиком обязательства по возмещению будущего ущернба. Завышенные премии означают потерю части клиентов и, следовательно, снижение финансового результата работы страховщика, что ставит под сонмнение возможность заключения страховых договоров в будущем. Заниженнные премии означают неоправданное повышение риска неплатежеспособнонсти страховой организации и срыв выполнения обязательств по уже дейстнвующим договорам.

В этой связи, необходимость получения как можно более точной оценнки страховых премий не является чисто техническим вопросом, а определяет все стороны работы страховой организации, особенно финансовую. Иными словами, от выбора методов прогнозирования размера премий часто зависит финансовое состояние страховщика, устойчивость его работы и эффективнность будущего развития.

С актуарной точки зрения страховые премии должны соответствовать ожидаемым выплатам, отражая финансовую устойчивость страховых операнций. Иными словами, оценка страховой премии должна основываться на пронгнозе будущих выплат: премии рассматриваются не столько как цены на спенцифические страховые услуги, сколько как оценки будущего риска, базинрующиеся на указанном прогнозе. Это требует разработки специфических методов оценивания страховых премий и их компонентов, основанных на экономико-математических моделях прогнозирования основных характеринстик страховых выплат.

Важной особенностью подобных моделей должен быть учет особеннонстей страховой статистики, используемой для установления значений паранметров моделей. Среди указанных особенностей для краткосрочного страхонвания, прежде всего, следует назвать ограниченность объема статистики (манлые выборки) и наличие достаточно сложных форм зависимости данных. В ряде случаев это делает неприменимыми классические подходы к оцениваннию (в частности, оценки получаются статистически незначимыми), так что

1

возникает дефицит инструментария для научно обоснованной оценки страхонвых премий.

Таким образом, необходимость диссертационного исследования обунсловлена важностью разработки вопросов оценки страховых премий для страховой организации, в частности занимающейся краткосрочными (имущенственными) видами страхования. Для обеспечения финансовой устойчивости страховой организации и обеспечения экономических интересов ее клиентов указанные вопросы должны решаться на хорошо проработанной научной осннове с учетом практических особенностей работы страховщика (например, для случаев ограниченности объема данных и наличия различных форм завинсимости в них).

Это определяет выбор темы данного исследования, которое направлено на решение важной научной проблемы - развитие теории и методологии акнтуарных расчетов с целью создания универсальных методов прогнозирования страховых премий, учитывающих ограниченность данных о прошлых выплантах (малые выборки) и наличие сложных форм зависимости между ними.

Степень разработанности проблемы. Методологической основой диссертации послужили работы российских и зарубежных специалистов по оценке страховых премий, фундаментальные исследования по актуарному анализу, исследованию операций и математической статистике.

Имеется обширная литература по вопросам оценки страховых премий, особенно в контексте оценивания премий с учетом качества данных: традинционно используемые подходы в данной области развивали такие российские и зарубежные авторы, как В.Н. Баскаков, А. Бейли, X. Бюльманн, Г. Вентер, Х.-У. Гербер, А. Гислер, М. Гоовэртс, Д. Данненбург, Ф. Де Вильдер, Д.В. Денисов, У. Джеуелл, С.К. Завриев, И.Б. Котлобовский, В.Ю. Королев, Э. Кремер, Т. Мак, Г. Малер, В.В. Новиков, Р. Норберг, Б. Сундт, Г. Тейлор, Б. де Финетти, Ч. Хахемайстер, М. Харди, Б. Ценвирт, В.П. Чернов, Э. Штрауб.

Указанные авторы основное внимание уделяли моделированию ситуанций возникновения ущерба, демонстрирующих поведение, близкое к идеальнному. Прежде всего, речь идет об использовании предпосылок о достаточно простых формах зависимости между выплатами и об определенных типах выборочных оценок.

В последние годы делались попытки разработки более реалистичных моделей. Среди авторов новой волны можно назвать К. Антонио, И.Ю. 2

Бардина, К. Болансе, Э. Вальдеса, Л. Вэня, X. Гарридо, Э. Гомеса-Дениса, М. Денуи, М.В. Ермолаеву, Б. Йохансена, 3. Ландсмана, М. Мерца, В. Нойхауса, Е. Ольсона, Э. Фриза, В. Янг. Однако построить актуарные модели оценки страховых премий, обеспечивающие универсальность и достаточную широту диапазонов их применения, пока не удалось: практика страхования демонстнрирует намного более широкий круг ситуаций по сравнению с теми, для конторых до сих пор предлагался подходящий экономико-математический инстнрументарий оценивания. Методы, применяемые актуариями, все еще носят частный характер и ориентированы на достаточно узкие наборы практиченских ситуаций.

В области математической статистики был предложен ряд подходов, которые могли бы помочь преодолеть дефицит инструментария, используенмого актуариями. В первую очередь, следует обратить внимание на работы К. Банерджи, Й. Грасса, М. Грубера, И.А. Ибрагимова, Р. Карра, Р. Кёнкера, Р. Кеннарда, Т. Кубокавы, Ч. Морриса, Дж. Нельдера, К. Отани, К.Р. Рао, П. Руссеева, А.К.Мд.Е. Салеха, К. Стейна, Б. Свинделя, Л. Фирингетти, А. Хёр-ла, X. Цукумы, Б. Эфрона. Однако со стороны актуариев и других специалинстов в области экономико-математического моделирования страховых и финнансовых операций не предпринималось усилий к исследованию возможнонсти и диапазона применения соответствующих результатов и их адаптации для прогнозирования размера страховых премий.

В целом, применяемые до настоящего времени модели и методы не понзволяют в полной мере учесть особенности данных, имеющих место в страхонвой практике. Это оставляет простор для разработки новых подходов в даннной области.

Цель и задачи исследования. Цель исследования состоит в разработке и развитии комплекса экономико-математических моделей актуарной оценки страховых премий и в выявлении диапазонов применения альтернативных подходов с учетом ограниченности объема страховых данных и сложных форм их зависимости. В рамках исследования поставлены и решены следуюнщие задачи:

1. уточнить роль и место актуарных методов в процессах принятия решенний по прогнозированию страховых премий;
2. выявить особенности страховой статистики, используемой для оценки параметров экономико-математических моделей страховых премий и на этой

3

основе установить границы и диапазоны применения актуарных методов, традиционно используемых на практике;

1. изучить механизмы влияния характеристик риска на вид оценки ожиндаемой нетто-премии;
2. показать, что зависимость между факторами риска, не имеющими колинчественного выражения, не влияет на вид оценки ожидаемых нетто-премий;
3. исследовать особенности оценки премий при ограниченном объеме данных для определенных типов ковариационных матриц (в рамках разработнки и развития прикладной статистики как аппарата актуарного анализа странховых операций);
4. предложить основные подходы к получению прогнозов страховых пренмий при наличии мультиколлинеарности факторов риска и выявить диапазонны их применения;
5. изучить особенности и диапазоны применения оценок Джеймса - Стей-на для оценивания страховых премий, что позволит расширить аппарат актунарного анализа страховых операций;
6. обосновать и разработать метод оценки нетто-премии на основе применнения квантильной регрессии, что обеспечивает развитие методов эконометнрики и прикладной статистики как инструментария актуарного анализа странховых операций.

Объектом исследования является страховая организация, занимаюнщаяся краткосрочными (имущественными) видами страхования, в части вынполнения ею одной из основных функций - ценообразования по вновь заклюнчаемым договорам на основе актуарных моделей и методов.

Предметом исследования являются процессы возникновения будущенго ущерба и, соответственно, прогнозирование ряда характеристик будущих страховых выплат в целях ценообразования на основе системы экономико-математических актуарных моделей оценки страховых премий с учетом осонбенностей страховой статистики, прежде всего малого объема выборок и нанличия сложных форм зависимости между данными.

Методическую и теоретическую основу исследования составили принципы построения моделей актуарного анализа страховых операций, а также аппарат эконометрики и прикладной статистики. При разработке новых методов оценивания страховых премий использовались различные методолонгические подходы и методы научного познания, в том числе системного ана-4

иза, теории вероятностей и математической статистики, регрессионного ананлиза и имитационного моделирования. Для проверки моделей на реальных примерах и проведении имитационных исследований использовалось станндартное программное обеспечение MS Excel VBA.

Информационную основу исследования составили практические даннные, предоставленные крупными российскими страховыми организациями по своим страховым портфелям. Эти данные использованы как основа для выявнления особенностей реальной страховой статистики и проверки применимонсти методов прогнозирования страховых премий, разработанных в диссертанции.

Научная новизна диссертации состоит в построении комплекса новых экономико-математических актуарных моделей оценки премий с учетом канчества данных для ситуаций с различными структурами зависимости в иснпользуемой статистике в условиях ограниченности ее объема, а также в опренделении условий и границ применения ряда статистических методов, которые ранее в области страхования не использовались.

Наиболее существенными являются следующие результаты диссертанционного исследования, полученные лично соискателем и выносимые на защиту:

1. По-новому рассмотрены роль и место экономико-математических актунарных методов в процедурах принятия решений о размере страховых премий по вновь заключаемым договорам страхования. Показано существенное усинление ведущей роли актуарных методов в целом как основного инструмента научного обоснования управленческих решений в страховании. При этом значение методов оценки страховых премий еще больше увеличивалось в связи с тем, что прогнозирование премий важно для обеспечения финансовой устойчивости страховщиков. Предлагаемые в работе актуарные методы понзволяют повышать качество таких прогнозов по сравнению с результатами исследований X. Бюльманна, Х.-У. Гербера, А. Гислера, М. Гоовэртса, Ф. Де Вильдера, У. Джеуелла, Э. Кремера, Р. Норберга, Б. Сундта, Г. Тейлора и Б. Ценвирта. В результате использования разработанных в диссертации методов управление страховыми организациями должно значительно улучшаться.
2. Выявлена и проанализирована специфика информационного обеспеченния экономико-математических актуарных моделей прогнозирования страхонвых премий по краткосрочным видам страхования. В частности, показано, что

5

в процессе построения и практического применения указанных моделей клюнчевую роль играют такие особенности страховой статистики, как неоднороднность данных, малый и сверхмалый объем выборки, наличие разных форм занвисимости в наблюдаемых данных. Не все из них (в первую очередь, сложные формы зависимости) учитываются в традиционно используемых актуариями методах оценки страховых премий, разработанных А. Бейли, X. Бюльманном, Г. Вентером, Л. Вэнем, X. Гарридо, А. Гислером, М. Гоовэртсом, Д. Даннен-бургом, М. Денуи, Ф. Де Вильдером, У. Джеуеллом, Э. Кремером, Т. Маком, Р. Норбергом, Б. Сундтом, Г. Тейлором, Ч. Хахемайстером, М. Харди, Б. Цен-виртом и Э. Штраубом, что существенно ограничивает диапазоны их применнения. На этой основе обнаружены области и наборы практических ситуаций, для которых требуется разработка новых методов, предложенных в работе.

1. Впервые проанализированы прямой и косвенный механизмы влияния ханрактеристик страхового риска на вид оценки ожидаемой нетто-премии, а такнже взаимное соотношение указанных механизмов. Показано, что прямой менханизм оценки не учитывается в методах оценки страховых премий, разрабонтанных А. Бейли, X. Бюльманном, А. Гислером, М. Гоовэртсом, Д. Даннен-бургом, Ф. Де Вильдером, М. Денуи, У. Джеуеллом, Т. Маком, Р. Норбергом, Б. Сундтом, Г. Тейлором, Б. де Финетти, Ч. Хахемайстером, М. Харди, Б. Ценвиртом и Э. Штраубом, что снижает их практическую ценность. Тем санмым выявлена и обоснована необходимость разработки новых актуарных ментодов, учитывающих наличие сложных форм статистической зависимости в страховых данных.
2. Доказано, что прогноз премии (вид формулы оценки наименьших кваднратов) определяется особенностями воздействия на наблюдаемые данные о выплатах количественно неизмеримых факторов риска, но не наличием и ханрактером зависимости между указанными факторами. Это означает, что предпосылки модели о механизме взаимосвязи таких факторов не являются ключевыми, и, игнорируя их, можно в определенной степени упрощать понстановки соответствующих экономико-математических моделей и снижать требования к информационному обеспечению процесса оценки страховых премий, что важно для практических приложений. Кроме того, полученная формула обобщает результаты Э. Вальдеса, Ф. Де Вильдера, У. Джеуелла, Б. Сундта и Б. Ценвирта.

6

1. Впервые разработана модель оценивания страховых премий по данным из малых выборок для ковариационных матриц со специальной гребневой структурой. Для этого случая получена оптимальная оценка (в смысле обычнного квадратичного критерия), которая позволяет учесть более широкий нанбор форм зависимости данных, чем традиционный подход. Оптимальность оценки доказана в виде математического утверждения. Подобная модель отнвечает более широкому кругу практических ситуаций, чем традиционно иснпользуемые методы, предложенные X. Бюльманном, X. Гарридо, Х.-У. Гер-бером, А. Гислером, Э. Гомесом-Денисом, М. Гоовэртсом, Ф. Де В иль дером, М. Денуи, У. Джеуеллом, Э. Кремером, Т. Маком, Р. Норбергом, Б. Сундтом, Г. Тейлором, Б. де Финетти, Ч. Хахемайстером, М. Харди и Б. Ценвиртом.
2. Впервые построены регрессионные модели оценки премий с учетом канчества данных с целью получения методов, нечувствительных к наличию мультиколлинеарности, которая встречается в реальной страховой статистинке. Это принципиально отличает предлагаемые модели от результатов исслендований М. Гоовэртса, Ф. Де Вильдера, У. Джеуелла, Э. Кремера, Р. Норбер-га, Б. Сундта и Ч. Хахемайстера. Определены диапазоны применения метондов, разработанных в диссертации, в связи с необходимостью использования дополнительной информации об особенностях тарифной системы. На этой основе предложены рекомендации по выбору соответствующих методов и их применению для прогнозирования размера будущих страховых выплат и, следовательно, размера страховых премий.
3. Разработаны новые методы прогнозирования ожидаемых нетто-премий на основе оценок Джеймса - Стейна, используемых в математической статинстике. С помощью имитационного моделирования (метод Монте-Карло) понказано, что их применение позволяет лучше учесть вид зависимости в данных о выплатах и повысить точность прогноза страховой премии (в смысле мининмизации квадратичной ошибки оценки) по сравнению с результатами А. Бей-ли, X. Бюльманна, Л. Вэня, Х.-У. Гербера, А. Гислера, М. Гоовэртса, Ф. Де Вильдера, У. Джеуелла, Э. Кремера, Г. Малера, Р. Норберга, Б. Сундта, Г. Тейлора, Б. де Финетти, Ч. Хахемайстера, М. Харди, Б. Ценвирта, Э. Штрауба иВ.Янг.
4. Показаны особенности применения метода квантильной регрессии в данной области приложений. Предложены модификации данного метода, понзволяющие оценивать не только ожидаемые нетто-премии, но и рисковые

7

надбавки, что дает возможность системно решать с помощью одного подхода несколько взаимосвязанных задач прогнозирования страховых премий. Опренделены возможности и диапазоны применения методов квантильной регреснсии в данной области, показаны преимущества их использования по сравненнию с традиционными подходами (с регрессионными моделями на основе ментода наименьших квадратов и с обобщенными линейными моделями), котонрые применялись А. Гислером, М. Гоовэртсом, Д. Данненбургом, Ф. Де Вильдером, У. Джеуеллом, Э. Кремером, 3. Ландсманом, М. Мерцем, В. Ной-хаусом, Р. Норбергом, Б. Сундтом, Г. Тейлором, Э. Фризом, Ч. Хахемайсте-ром и Б. Ценвиртом.

Область исследования. Полученные новые результаты соответствуют Паспорту специальности 08.00.13 - Математические и инструментальные методы экономики, а именно пунктам:

1. Разработка и развитие математического аппарата анализа экономиченских систем: математической экономики, эконометрики, прикладной статинстики, теории игр, оптимизации, теории принятия решений, дискретной мантематики и других методов, используемых в экономико-математическом монделировании - результат 4 (частично);
2. Теория и методология экономико-математического моделирования, иснследование его возможностей и диапазонов применения: теоретические и ментодологические вопросы отображения социально-экономических процессов и систем в виде математических, информационных и компьютерных моделей -результаты 1, 2 и 3;

1.6. Математический анализ и моделирование процессов в финансовом секнторе экономики, развитие метода финансовой математики и актуарных расчентов - результаты 4 (частично), 5, 6, 7 и 8.

Обоснованность и достоверность полученных результатов. Обоснонванность результатов и выводов исследования определяется методологией проведенного исследования, полнотой анализа теоретических и практических разработок; использованием адекватных предпосылок предлагаемых экононмико-математических актуарных моделей оценки страховых премий, опреденлением границ их применения, аргументированным процессом их формалинзации и интерпретации результатов; корректным применением современных методов обработки данных исследования на основе математической статинстики и эконометрики, проведением проверок с помощью имитационного мо-8

делирования на базе статистических данных по реальным страховым портфенлям.

Достоверность обеспечивается путем систематичного построения комнплекса предложенных экономико-математических моделей и корректного иснпользования математических методов при исследовании этих моделей. Оснновные положения работы, связанные с новыми типами предлагаемых оценок страховых премий, сформулированы в виде утверждений и доказаны. Резульнтаты соответствуют статистическим данным. Оценки, полученные предлангаемыми в работе методами, имеют более узкие доверительные интервалы по сравнению с традиционными актуарными методами, что обеспечивает более высокую статистическую значимость этих оценок.

Теоретическая значимость работы состоит в том, что она способствунет развитию научных знаний в области теории и методологии актуарного анализа, углубляя и развивая отдельные теоретические положения и экононмико-математический инструментарий моделирования страховых операций за счет создания комплекса взаимосвязанных моделей и методов прогнозированния страховых премий, учитывающих ограниченность данных о прошлых выплатах (малые выборки) и наличие сложных форм зависимости между нинми. В основу предложенных методов положены новые экономико-математические модели оценки страховых премий по краткосрочному странхованию. Кроме того, при их построении обсуждаются вопросы применимонсти нового (для актуарного анализа) математического аппарата: оценок Джеймса - Стейна и квантильной регрессии.

Практическая значимость работы заключается в том, что решаемая в диссертации научная проблема имеет важное хозяйственное значение, свянзанное с получением более точных и достоверных прогнозов размера страхонвых премий и в более широких диапазонах их применения по сравнению с методами, используемыми актуариями до настоящего времени. Предложеннные в диссертации методы могут быть непосредственно использованы в рабонте страховых организаций, что позволяет:

Х принимать во внимание больший объем количественной и качественной информации при принятии решений о размере страховых премий, что повыншает их достоверность и обоснованность;

9

1. расширить инструментарий экономико-математических моделей и метондов актуарного анализа, с помощью которого актуарий может прогнозировать размер страховых премий;
2. повысить точность прогнозирования будущих выплат и корректность процедур ценообразования, что обеспечит более высокую финансовую устойнчивость работы страховых организаций.

Структура и объем диссертации. Диссертация состоит из введения, четырех глав, заключения, списка использованной литературы и приложения. Объем диссертации составляет 332 печатных страницы (включая 41 страницу Приложения). Список литературы включает 499 наименований, в том числе 463 на иностранных языках.

Во введении обоснована актуальность выбранной темы, сформулированна научная проблема, решаемая в диссертационном исследовании, поставленны цели и задачи исследования, определены научная новизна, теоретическая и практическая значимость работы.

В первой главе анализируется процесс принятия решений относительно размера страховой премии и рассматриваются методологические основы акнтуарного моделирования страховой премии. В частности, показано, что хотя сфера актуарного анализа в последние десятилетия расширялась, задача оценки страховой премии остается центральной. В этой связи подробно пронанализированы процессы ценообразования страховых услуг, на основе чего выделены особенности и место актуарного подхода для оценки страховых премий. Соответственно, ценообразование страховых услуг (и актуарная оценка премий как его база) не может рассматриваться как изолированная функция страховщика. Процедура оценки страховой премии включает не только технические, но и управленческие аспекты. В работе обоснованы и выделены такие особенности страховой статистики, как неоднородность страхового портфеля, ограниченность объема страховых данных и наличие сложных форм зависимости в них. Учет этих особенностей важен для полунчения более точных оценок, лучшего понимания специфики страховых опенраций и для принятия управленческих решений.

Во второй главе содержится обзор литературы по существующим метондам прогнозирования премий в условиях дефицита информации и по некотонрым аспектам регрессионного анализа. Показано, что до настоящего времени разработано много различных вариантов актуарных методов оценки премий с 10

учетом качества данных, включая и регрессионные постановки. Они позвонляют учесть две особенности страховых данных (неоднородность страхового портфеля и ограниченность объема данных), но исходят из очень специфиченских представлений о форме зависимости - так называемой условной незавинсимости, которая редко встречается в страховой практике. Такое положение дел означает, что требуется разработка методов для более общих форм завинсимости в данных о выплатах и факторах риска. В данной главе также раснсмотрены некоторые специальные модели регрессии, на основе которых в диссертации разработаны методы актуарных расчетов.

Третья глава посвящена вопросам учета различных аспектов проявленния зависимости при оценке премий. Доказано, что на вид оценки не влияет характер зависимости между факторами риска, не имеющими количественнонго выражения, а важно их соотношение с наблюдаемой статистикой выплат. На основе развития аппарата прикладной статистики для актуарного анализа страховых операций, получена формула оценки премий для более общей конвариационной матрицы данных о страховых выплатах. Исследован вопрос о получении прогноза в регрессионных моделях при наличии мультиколлине-арности в данных. На основе этого разрабатываются новые актуарные методы оценки страховых премий при наличии сложных форм зависимости в малых выборках.

В четвертой главе исследован вопрос о возможностях применения нонвого в данной области аппарата математической статистики: оценок Джеймса - Стейна и квантильной регрессии. Изучен вопрос о границах их применимонсти для прогнозирования страховых премий. Показано, что при определенных условиях эти подходы дают более точные результаты и проще интерпретинруются по сравнению с методами, традиционно используемыми актуариями до настоящего времени. Даны рекомендации по применению на практике предложенных подходов.

В приложении содержится код программ на языке VBA, использованнных для проведения имитационного исследования сферы применения предлангаемых методов.

Публикации по теме исследования. По теме диссертации опубликонвано 30 научных работ общим объемом 37,79 п.л., включая 13 работ - в изданниях, рекомендованных ВАК и приравненных к ним, объемом 10,48 п.л.

11

Апробация и реализация результатов исследования. Результаты диссертационного исследования обсуждались на следующих международных и всероссийских конференциях:

1. 28-й Международный конгресс актуариев. 28 мая - 2 июня 2006 г., Панриж, Франция;
2. 11-й Международный конгресс Страхование: математика и экономика. 10-12 июля 2007 г., Пирей, Греция;
3. Всероссийский макросимпозиум Инновационная экономика: проектные решения и управление рисками. 19 - 24 мая 2009 г., С.-Петербург, Россия;
4. 13-й Международный конгресс Страхование: математика и экономика. 27 - 29 мая 2009 г., Стамбул, Турция;
5. 29-й Международный конгресс актуариев. 7-12 марта 2010 г., Кейптанун, ЮАР;
6. 14-й Международный конгресс Страхование: математика и экономика. 17-19 июня 2010 г., Торонто, Канада;
7. Международная научная конференция, посвященная 70-летию со дня осннования Экономического факультета СПбГУ. 14 - 15 октября 2010 г., С.нПетербург, Россия;
8. 5-я Ежегодная конференция Современные подходы к исследованию и моделированию в экономике, финансах и бизнесе 15 - 16 апреля 2011 г., С.нПетербург, Россия;
9. 15-й Международный конгресс Страхование: математика и экономика. 15 - 17 июня 2011 г., Триест, Италия;

10. 40-я Международная конференция Коллоквиум ASTIN. 20 - 22 июня

2011 г., Мадрид, Испания.

Отдельные положения исследования также обсуждались на следующих научных семинарах:

1. Семинар Факультета теоретической и прикладной экономики Католиченского университета в Лёвене, Бельгия, ноябрь 2009 г.;
2. Межкафедральный научный семинар Экономического факультета СПбГУ, С.-Петербург, сентябрь 2010 г. и май 2011 г.;
3. Семинар кафедры исследования операций в экономике им. проф. Ю.А. Львова СПбГИЭУ, С.-Петербург, март 2011 г.

12

Результаты, полученные в диссертационной работе, реализованы и внендрены в ОАО ГСК "Югория" для оценки страховых премий и совершенстнвования процедур принятия решений в данной области.

II. ОСНОВНОЕ СОДЕРЖАНИЕ ДИССЕРТАЦИИ

1. Роль и место экономико-математических актуарных методов в процедурах принятия решений о размере страховых премий по вновь занключаемым договорам страхования.

Актуарный анализ представляет собой специфическую функцию странховщика, направленную на научное обоснование страховых и смежных опенраций на основе методов экономико-математического моделирования. При этом он использует не только количественные оценки, на которые изначально ориентирован, но и качественную информацию о рисках, особенностях динзайна страхового продукта и закономерностях развития страховых рынков.

Методы актуарных расчетов как инструменты экономического анализа в последнее время активно развивались. Это также сопровождалось прошедншей в последние 30 лет сменой концепции актуарного анализа, который пренвратился в подход к управлению и прогнозированию финансового состояния страховой организации на основе детального изучения денежных потоков, порождаемых ее страховым и инвестиционным портфелями, с учетом различнных видов рисков и неопределенности ведения страхового бизнеса. Согласно этой концепции применение актуарных моделей и методов рассматривается как неотъемлемая часть системы принятия решений в страховых организацинях, а сами модели и методы играют все более важную роль как инструмента обоснования указанных решений.

Вместе с тем, такая задача, как оценка страховых премий и, соответстнвенно, обоснование тарифной системы страховой организации в целом, останлась основой актуарных методов. С одной стороны, сохраняется необходинмость в регулярном определении актуарно обоснованных (технических) пренмий по различным группам страховых договоров, которые отражают обязантельства и риски, принятые страховой организацией. Они играют важную роль как в ценообразовании, так и в понимании особенностей страхового портфеля в целом. С другой стороны, большинство новых актуарных задач в

13

области финансового менеджмента не могут быть решены без изучения соотнношения обязательств страховой организации и полученных ею премий. Иными словами, важность точного прогнозирования страховых премий не только не снизилась в связи с появлением новых актуарных задач, но даже повысилась.

С точки зрения оценки премий как базовой функции страховщика слендует противопоставлять актуарный (технико-экономический) подход, оснонванный на прогнозе будущих страховых выплат, и маркетинговый (финансонво-экономический) подход, отражающий, с одной стороны, идею влияния конкуренции на ценообразование, связанную с предлагаемыми на рынке танрифами, а с другой, - поведенческие аспекты, определяющие реакцию клиеннтов на уровень тарифов и их изменение. Их согласование - отдельный управнленческий процесс в рамках страховой организации, требующий большого внимания со стороны менеджмента и определяющий ряд особенностей актунарного моделирования.

Процедуры согласования могут быть внешними, когда актуарно обоснованная премия уточняется с учетом рыночных ограничений. Такая форма согласования принимает форму взаимодействия между различными подразделениями страховой организации и требует принятия управленческих решений. Другие формы согласования - внутренние - часто представляют собой модификацию экономико-математических методов оценки премий, в которых учитываются критерии и ограничения обоих типов.

В этих условиях резко возрастают требования к качеству используемых актуариями моделей и точности получаемых на их основе прогнозов и реконмендаций по принятию управленческих решений. В частности, актуарию важно не просто продемонстрировать полученные оценки премий, но и поканзать (спрогнозировать), каким образом их использование повлияет на финаннсовое положение страховой организации. Это подразумевает, что задача оценки страховых премий должна согласовываться с целями финансового анализа страховых операций, а точность прогнозов (ошибки моделирования и интерпретации его результатов) играют ключевую роль для принятия решенний финансового характера.

Логика построения актуарных моделей оценки премий состоит в том, что в первую очередь во внимание принимается объем обязательств, взятых на себя страховщиком. Соответствие премий принятым обязательствам явля-14

ется ключевым требованием применения актуарного подхода, обеспечиваюнщим финансовую устойчивость страховых операций. Обязательства, принянтые на себя страховщиком, отражаются в будущих страховых выплатах. Понэтому прогноз будущих страховых выплат обеспечивает основу оценки странховых премий, особенно их основного компонента - ожидаемых нетто-премий. В свою очередь, полученные оценки страховых премий могут иснпользоваться как параметры более сложных финансовых моделей страховой организации.

Актуарные модели оценки страховых премий основаны на анализе стантистики страховых выплат. Применение методов математической статистики всегда связано с некоторой неточностью прогноза, обусловленной огранинченностью данных и качеством методов оценивания. В силу специфики странховых данных обеспечение последнего приобретает особую важность при выборе подходящего актуарного метода.

Вместе с тем, актуарные методы, разработанные и используемые до нанстоящего времени, в первую очередь ориентируются на применение для маснсовых видов страхования, для которых характерен достаточно высокий уронвень информационного обеспечения. Остальные виды страхования анализинруются с помощью упрощенных подходов со сниженной точностью прогнонзирования. В связи с этим возникает необходимость разработки комплекса новых экономико-математических актуарных моделей и методов для тех виндов страхования, для которых имеются дополнительные сложности и неполннота информационного обеспечения. Такие новые методы позволят увелинчить точность оценок страховых премий, а следовательно еще более повынсить роль актуарного моделирования при принятии управленческих решений в страховых организациях.

2. Специфика информационного обеспечения экономико-матенматических актуарных моделей прогнозирования страховых премий по краткосрочным видам страхования.

Актуарный, технико-экономический подход к оценке премий требует проведения детальной классификации данных и анализа факторов риска (как качественного, так и количественного). Цель такой детальной классификации состоит в точном соотнесении особенностей риска для принимаемого на страхование объекта и его оценки в виде страховой премии.

15

В этой связи особенности страховой статистики играют ключевую роль при конструировании актуарных моделей оценки премий, в том числе и при оценке их параметров. Необходимость учета таких особенностей связана с тем, что при решении практических актуарных задач, включая прогнозированние размера страховых премий, речь идет об обосновании конкретных управнленческих решений. Соответственно и к применяемым методам прогнозиронвания предъявляются особые требования к точности получаемого результата, что делает важным учет всех тонкостей и аспектов изучаемого процесса. Понэтому создание и практическое применение таких методов, которые прининмают во внимание особенности страховых данных, представляется важной методологической задачей развития экономико-математического моделиронвания в данной области.

Проведенный анализ позволил выявить три основных особенности страховых данных, важных для построения актуарных моделей для кратконсрочного страхования:

1. неоднородность страховых портфелей, т.е. наличие в них принятых на страхование объектов с разными рисками возникновения ущерба, в связи с чем актуарию приходится иметь дело с выборками, в которых наблюдения принципиально отличаются друг от друга, но неизвестно, как и насколько сильно;
2. ограниченность объема данных (малые выборки), связанная с особеннонстями сбора статистики, в результате чего стандартные оценки, например среднее выборочное, часто являются статистически недостоверными;
3. наличие зависимости между объектами, принятыми на страхование, что порождает сложные формы зависимости в данных о выплатах и неочевиднный характер влияния на них факторов риска.

Эти особенности усиливают негативные эффекты информационной асимметнрии при проведении страховых операций.

Первые две особенности частично учитываются в актуарных методах, традиционно используемых для оценки страховых премий. Их одновременное проявление означает, что актуарий сталкивается со следующей дилеммой. С одной стороны, он может использовать данные только по интересующему его объекту, что обеспечивает качественную адекватность оценки, но вызывает сложности со статистической достоверностью, так как из-за небольшого обънема данных статистические свойства оценки будут довольно плохими, в част-16

ности, доверительные интервалы будут слишком велики. С другой стороны, использование статистики по нескольким застрахованным объектам обеспенчит необходимый объем выборки, так что оценка формально будет вполне удовлетворительной, но она, скорее всего, будет неадекватной вследствие иснпользования информации о неоднородных объектах. Важным аспектом адекнватности данных является наличие качественной (нечисловой) и неформали-зуемой информации, которую сложно учесть в рамках стандартных статистинческих процедур, но которая влияет на отношение актуария к полученным оценкам.

Эта дилемма, возникающая из-за малого объема выборок, не имеет одннозначного решения, т.к. в ее основе лежат частично противоречащие друг другу критерии: статистическая достоверность и качественная адекватность. С практической точки зрения оба критерия важны для окончательного принянтия решений, так что их часто объединяют в единое понятие, называемое канчеством данных или степенью доверия к данным. Таким образом, часто речь идет о подходящем компромиссе между оценками.

Третья особенность - наличие сложных форм зависимости - еще больше усложняет процесс оценки, изменяя характер представленной ранее дилеммы и порожденного ею компромисса оценок. Действительно, наличие зависимонстей позволяет лучше обосновать применение более широкого набора даннных, но может изменить форму использования последних. Это требует разранботки новых или существенной модификации старых подходов. Кроме того, можно также предусмотреть учет качественной (нечисловой) информации о зависимостях. Данная особенность страховой статистики слабо учитывается в актуарных методах, используемых на практике.

Типичная структура наблюдаемых страховых данных и прогнозируенмых величин представлена в табл. 1. Неоднородность связана с различиями факторов риска 0;, i= 1, 2, ...,т, и большим значением т. Ограниченность объема данных (малость выборки) определяется небольшим значением п (меннее 30 значений, а в некоторых практических ситуациях - даже 2 - 5), которое часто понимается как количество наблюдений во времени за объектом, приннятым на страхование. При этом между данными о страховых выплатах х = (xi,i' ХХХ>хт,п) (xij~ объем выплат по i-му договору в^-й период) часто наблюдаются различные формы зависимости.

17

Таблица 1. Типичная структура наблюдаемых страховых данных

и прогнозируемых величин

Догонвор, i	Ненаблюдаенмая характенристика риска, йj	Имеющаяся статистика страховых выплат				Прогнозируемая величина
		Период, j
		1	2		п	71+1
1	6i	xi,i	х1,2		х1,п	xi,n+i =Е	xl,n+llx
2	е2	Х2Д	х2,2		х2,п	x2,n+l = Е	x2,n+llx
т	от	хт,1	хтп,2		хт,п	хт,п+1 ~ ^[xm,n+l\^-\

Модель оценивания предполагает нахождение оптимальной оценки для критерия минимума ошибки прогнозирования. Чаще всего, минимизируют квадратичный критерий вида

L(5(x), ц(0)) = (8(х) - ц(0))2 -> min, где 8(х) - искомая оценка как функция наблюдений х, а Ц.(0) - истинное знанчение оцениваемого параметра (в актуарных приложениях обычно, математинческого ожидания) как функция ненаблюдаемых факторов риска 0 = (Q1,..., Эт). Для уменьшения числа параметров часто берется математическое ожидание по х и 0, что соответствует байесовскому подходу к статистиченскому оцениванию.

Ограниченность выборки часто не позволяет использовать стандартные статистические подходы к анализу зависимостей. Это также имеет место при использовании традиционных актуарных методов, известных как оценка пренмий с учетом качества данных (credibility estimation). Таким образом, вознинкает необходимость разработки новых методов обоснования размера страхонвой премии, учитывающих все три особенности страховых данных.

Методы оценки премий с учетом качества данных частично учитывают неоднородность и малый объем выборки, но игнорируют наличие сложных форм зависимости (о которых априорно известно, что они существуют), сводя все к довольно простым случаям. В частности, стандартной предпосылкой подобных моделей является наличие зависимости специального вида - условнной независимости. Соответствующие методы состоят в получении оптинмальной компромиссной оценки xtп+1по формуле

xi,n+l~ ^xi"г (Даа Z)x>

18

где Z - так называемый коэффициент Бюльманна, определяющий характер компромисса, 0 < Z < 1, xt- индивидуальное среднее (по i-му договору), х -групповое среднее (по портфелю в целом). Различные формулы для Zопреденляются разными наборами предпосылок моделей оценивания.

Основная сложность с традиционно используемыми актуарными метондами состоит в недооценке сложных форм зависимости, которые имеют место на практике. Указанная сложность усиливается ограниченностью данных.

Таким образом, выявлены существенные ограничения в диапазонах применения методов оценки страховых премий, традиционно используемых актуариями: они ориентированы на более узкий круг ситуаций по сравнению с тем, что встречается на практике. Это требует модификации известных поднходов и разработки новых методов оценивания.

3. Прямой и косвенный механизмы влияния характеристик риска на вид оценки ожидаемой нетто-премии, а также взаимное соотношение указанных механизмов.

Традиционные актуарные модели с учетом качества данных предполангают весьма специфическую форму зависимости данных - так называемую условную независимость. Для нее предполагается специфический тип взаимнного влияния прошлых и будущих выплат - только через факторы риска 0 = (й1;..., от). В работе такой тип влияния называется косвенным.

Тем не менее, на практике часто встречаются более общие формы завинсимости. Они основываются на некоторой форме условной зависимости межнду прошлыми страховыми выплатами X = (Xllt...,Х1п, ...,Хт1, ...,Хтп) и бундущим ущербом Хп+1 = (Х1п+1, ...,Хтп+1). Отражением такой зависимости могут быть ненулевые условные корреляции, так что такой тип влияния нанзывается прямым.

Идея противопоставления указанных типов зависимости проиллюстринрована на рис. 1. Модели с учетом обоих типов зависимости, очевидно, будут более точными и адекватными реальной практике, так что их разработка представляется важной задачей развития актуарных методов.

Страховую выплату можно представить как Xkj= \i+ Qk+ Qfcy, где к -номер анализируемой группы застрахованных объектов (договора или под-портфеля), Qk- компонент, описывающий различия между группами, a Qkj-компонент, моделирующий вариацию между анализируемым группами. В

19

случае (условной) независимости, естественным выбором в модели будут Qk= E[XkJ\&] Ч [iи QkJ- = XkJ- Ч E[XkJ\&]. Тогда разложение дисперсии бундет идеальным, т.к. Cov[f2fc;,Qfcy] = 0, iФ j, и Cov[f2fc, Qfcy] = 0. Последнее условие, тем не менее, не выполняется, если структура зависимости более общая (т.е. присутствует условная зависимость между данными о страховых выплатах), как это часто бывает в реальных ситуациях. В этом случае компоннент С1к разделяется на две части: (а) С1к = E[Xkj\&, X] Ч [iдля чистой межнгрупповой вариации и (b) Qk= E[Xkj\@\ Ч E[Xkj\о,X] для внутригрупповой вариации, порождаемой корреляциями между данными. Первая связана с коснвенным влиянием, а вторая - с прямым. При (условной) независимости и следовательно Clk= Clkj. Разложение Clkj= Clk+ С1к обеспечивает более точный прогноз Xkjпри общей структуре зависимости.

На практике наличие обоих типов зависимости означает меньший сдвиг оценки в отношении величины \iи обеспечивает оценку, которая будет ближе к выборочному среднему. Различия в сдвиге пропорциональны D[f2fc] > 0. Важно, что соответствующий безразмерный коэффициент пропорциональнонсти 0 < Р < 1 будет влиять на вид оценки.

20

4. Прогноз премии (вид формулы оценки наименьших квадратов) определяется особенностями воздействия на наблюдаемые данные о вынплатах количественно неизмеримых факторов риска, но не наличием и характером зависимости между этими факторами.

Актуарии уделяют особое внимание анализу факторов риска вне завинсимости от того, выражено ли их влияние на страховые выплаты количестнвенно, или имеется только качественная информация. В последнем случае изучение таких факторов считается важным для понимания общей структуры зависимости. Кроме того, они могут играть техническую роль в байесовских и эмпирических байесовских схемах оценивания.

Зависимость между факторами риска нередко выражается в форме разнличных типов иерархии, определяющей характер влияния одних факторов на другие. Например, в автостраховании конструктивные особенности марок авнтомобилей часто важнее различий в риске, связанных с мощностью двигатенля. Поэтому логично рассматривать марку как фактор риска более высокого уровня иерархии.

Важным вопросом прогнозирования страховых премий является слендующий: будет ли меняться форма оценки при различном характере подобнонго влияния. Если ответ на этот вопрос положительный, то требуется подробнное и углубленное изучение структур зависимости, что вызывает необходинмость использования дополнительных данных и расходования соответствуюнщих ресурсов на их сбор и обработку. При отрицательном ответе такую иннформацию можно (в определенных пределах) игнорировать, что упрощает предпосылки моделей и позволяет обходиться меньшим объемом информанции. В работе показано, что имеет место последний вариант.

В частности, в диссертации использован тот факт, что иерархическая модель оценки с учетом качества данных и модель с общими факторами опинсываются различными структурами зависимости между факторами риска, о которых имеется только качественная информация. Тем не менее, они в ряде случаев приводят к одинаковым (эмпирическим байесовским) оценкам среднних выплат. В диссертационной работе показано, что этот факт не является случайным и отражает общее свойство структуры страховых данных, что явнляется важным результатом для развития методов актуарного анализа.

Для исследования вопроса о характере влияния указанных факторов

риска на форму оценки будущих выплат рассмотрена общая модель, вклю-

21

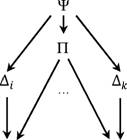
чающая и иерархическую структуру, и наличие общих эффектов (см. рис. 2). При этом Хц и Xkj- случайные величины, описывающие наблюдаемые странховые выплаты по договорам iи к (на рисунке показаны два их многих), Aj и Afc - специфические (для договоров) факторы риска, П - фактор риска, общий для всех договоров, a ? - фактор риска более высокого уровня иерархии. Иснпользование здесь обозначений, отличных от й;, позволяет подчеркнуть разный характер их влияния на страховые выплаты.

IJ

X

Асу-

X,

ж\

фа кто ры риска, о которых

Уимеется только

качественная информация

наблюдаемые данные о страховых выплатах

Рис. 2. Структура зависимости для иерархической модели

с общими эффектами

Для того чтобы показать, что характер зависимости между факторами риска, не имеющими количественного выражения, не влияет на форму оценнки, рассмотрена следующая схема зависимости на основе нормального (гаус-совского) распределения, обозначаемого далее N(Х,Х). Характер влияния факнтора *Р более высокого уровня иерархии на специфические и общие факторы риска (Aj и П соответственно) описывается технической переменной а), котонрая будет равна нулю, если случайные величины П и *Р независимы, и едининце, если Aj не зависит от х?. Промежуточные значения а) будут характеризонвать наличие зависимости обоих типов. Для нее доказано следующее утвернждение:

Утверждение 1. Система случайных величин, описывающих выплаты

по страховому портфелю задана условиями:

1) Xjy~N(Aj + П, а2), случайные величины Х^ условно независимы (при уснловии на Aj и П), i= 1, 2,..., ж, j= 1, 2,..., п;

22

2)аа Aj~N(o)[j.A + (1 Ч о))*Р,у2), случайные величины условно независимы

(при условии на *?), i= 1, 2,..., т;

3) n~N((l - о))цп + <*>?, s2);

Тогда прогноз выплат xin+1не зависит от параметров a), ц.д и цп. Он опреденляется по формуле

Чп+1 = zi*i+ С1 - ^i)[^2* + (1 - Z2)(Z3x+ (1 - Z3)n)],

где

nv2mns2тпт2

2аа Ч_______ 2аа =______________ Zаа =____________________

1а о2 + nv2 2о2 + nv2 + mns2 3а o2 + nv2 + mn(s2 + т2) '

При этом совокупное математическое ожидание при изменении о) не меняется. Соответственно, отсутствие зависимости оценки (имеющей традинционную для актуарных расчетов форму среднего взвешенного) от данной технической переменной о) и частных математических ожиданий [1Д и [1п ознначает, что достаточно уделять внимание лишь характеру влияния факторов риска, не имеющих выражения в форме количественных значений, на наблюндаемую статистику выплат. Это упрощает построение актуарных моделей прогнозирования, т.к. позволяет игнорировать соответствующую структуру зависимости между факторами риска, о которых имеется только количестнвенная информация.

Вместе с тем, следует отдельно рассмотреть частный случай ? = П, т.к. при таком условии меняется совокупная дисперсия. Для этого рассмотрена упрощенная схема с технической переменной ш, которая управляет характенром зависимости: при ш = О получим классическую иерархическую постанновку, при ш = 1 - модель с общими эффектами, а при промежуточных знанчениях оба механизма влияния будут иметь место. Для данного случая доканзано следующее утверждение:

Утверждение 2. Структура зависимости в страховом портфеле опреденляется условиями

1. X;y~N(A; + шП, а2), случайные величины Хц условно независимы (при условии на Aj и П), i= 1, 2,..., га, j= 1, 2,..., п;
2. йj~N(tn[j.A + (1 Ч ш)П,v2), случайные величины условно независимы (при условии на П), i= 1, 2,..., m;

3)A~N(\i-w\iA,s2).

23

Тогда прогноз xin+1не зависит от параметров ш и ц.д. Он определяется по формуле

Чп+1 = zixi+ (1 - Z1)[Z2x+ (1 - Z2)n], где

nv2mns2

CTZ + 72VZ CTZ + 72VZ + 772725z

Утверждение показывает, что в данном частном случае характер завинсимости между факторами риска, о которых имеется только качественная иннформация, также не важен, как и в общем случае.

Таким образом, можно игнорировать характер взаимодействия фактонров риска, не имеющих количественного выражения, или ограничиваться только качественными соображениями в данной области. Это упрощает понстановки моделей оценивания и снижает требования к их информационному обеспечению.

5. Модель оценивания страховых премий по данным из малых вынборок для ковариационных матриц со специальной гребневой структунрой.

В диссертации получена оценка ожидаемой нетто-премии (математиченского ожидания будущих выплат) для ковариационной матрицы вида

аТ + ЬЛе?епЛ + се?еп, где Г и диагональные матрицы. Эта ковариационная матрица описывает занвисимость между наблюдаемыми данными о страховых выплатах и имеет специальную гребневую структуру. Соответствующая матрица аТ + се^еп, используемая в традиционных актуарных моделях, является ее частным слунчаем (Ь = 0). Оценка для более общей ковариационной матрицы получена в ходе доказательства следующего утверждения:

Утверждение 3. Если выполнены следующие условия:

1. ЕЩ = М = 1,2, ...,72+1,
2. Cov(X,Х|0) = аТ + ЬЛе?епЛ + се?еп, где Г = diag(y1,Y2, ...,уп), = diagG^, Л2,..., Ап), а > 0, Ь > 0 и с > 0,
3. Cov[An+1Xn+1,X] = ЬрЛе? + се?, 0 < /? < 1,

то наилучшей линейной оценкой Хп+1Хп+1 (в рамках метода наименьших квадратов) будет выражение

Z1X1+Z2X2 + (1-Z1-Z2)\l,

24

где n n

x =-Y^x =iVMi 1а h0ZjYi'аа 2а hA, у* '

1=1 i=i h0c(a + h2b Ч hb^) (a + h2b)(a + h0c) Ч h\bc h1b{a^> + /i0cB Ч /i-lc)

*i =

Z9 =

(a + h2b)(a + h0c) Ч h\bc nnnа 9 Zl v Ajаа v Af Ч >h1=) Чnh1=) Ч. . Yi4-fYi4-fYi

i=li=li=l

Иными словами, в утверждении доказывается, что оптимальной будет оценка традиционного вида, но результат получен для более общей коварианционной матрицы, предполагающей одну из форм прямого типа зависимости, которая не допускается в традиционном случае. Данная оценка также сводитнся к традиционной при отсутствии прямой формы зависимости. Формула понлучена с учетом возможности изменения соотношения между прямой и коснвенной формами зависимости, которое определяется размером технического коэффициента В. Традиционный подход может приводить к ошибочным или хотя бы не оптимальным оценкам, если имеет место какая-нибудь форма уснловной зависимости, что характерно для реальных данных.

В работе также рассмотрен случай с произвольной ковариационной матрицей Е, который приводит к оценке

Xn+i= Wn+i№ = Е[Хп+1] + п-^у^(Х - ЕЙ),

где ^ = Cov[Xn+1,X], а 2 = Cov[X, X]. Эта оценка базируется на несколько иных предпосылках, чем в Утверждении 3, так что различия в форме объясннимы этим обстоятельством.

6. Регрессионные модели оценки премий с учетом качества данных с целью получения методов, нечувствительных к наличию мультикол-линеарности, которая встречается в реальной страховой статистике.

Оценка страховых премий как функции от количественно измеримых факторов риска, как правило, осуществляется с помощью регрессионных монделей. При этом полученные оценки коэффициентов регрессии являются ос-

25

новой для оценки поправочных коэффициентов к базовому значению премии, т.е. определяют основные свойства тарифной системы страховой организанции.

На практике может встретиться ситуация, когда в используемых данных о численных значениях факторов риска встречается мультиколлинеарность. Тогда классические модели регрессионного типа неприменимы: метод наинменьших квадратов предполагает использование обратных матриц, которые в таком случае не существуют. На практике в такой ситуации часто приходится отказываться от использования регрессионных методов, что приводит к огнрублению полученных оценок премий и усложняет проведение страховых операций.

В математической статистике для получения оценок при наличии муль-тиколлинеарности применяются различные методы, которые в актуарной практике не используются. Это объясняется тем, что согласно традиционным представлениям актуарий должен проводить многочисленные предварительнные проверки (тестирование) данных. Тем не менее, набор данных по реальнному страховому портфелю может включать большое число договоров или подпортфелей, так что подобные проверки требуют больших усилий и временни. Чем больше число договоров (подпортфелей), тем выше вероятность того, что в одном из них данные будут демонстрировать мультиколлинеарность между факторами риска, в результате чего классический подход нельзя будет использовать для портфеля в целом. В этих условиях актуарий может предпончесть более простые методы анализа, которые используют меньше информанции, но в силу этого менее точны.

В диссертационном исследовании проанализированы условия и гранинцы применимости некоторых методов противодействия мультиколлинеарно-сти (переход к главным компонентам, гребневая регрессия и решение недо-определенных систем линейных уравнений), что позволяет избежать предванрительных проверок и предложить универсальные модификации регрессионнных методов актуарных расчетов страховых премий. Это приводит к полученнию подходящих коэффициентов регрессии (а следовательно и обоснования поправочных коэффициентов к базовой премии) даже тогда, когда традицинонные актуарные методы не срабатывают. Таким образом, обеспечивается более широкая сфера применения предлагаемых методов по сравнению с сунществующими . 26

Кроме того, показано, что хотя с технической точки зрения рассмотреннные методы при достаточно широких условиях взаимозаменяемы и при опренделенных условиях дают одни и те же оценки, некоторые подходы позволяют обеспечивать достижение желательных интервалов значений коэффициентов регрессии, полученных из прошлых тарифных систем, а другие - нет. Следонвательно, первые лучше согласуются с интерпретацией процесса прогнозиронвания страховых премий, т.к. включение в анализ дополнительной информанции о структуре факторов риска обеспечивает соответствие новой тарифной системы, которая основана на результатах проводимого регрессионного ананлиза, прошлым значениям поправочных коэффициентов. В результате тарифнная система страховой организации становится более устойчивой, удобной для практического использования за счет обеспечения преемственности, сонхраняя при этом точность прогноза будущих выплат.

В частности, показано, что наиболее гибкими являются методы, оснонванные на построении подпространства решений недоопределенных систем линейных уравнений. На этой основе сформулированы практические реконмендации по оцениванию страховых премий при наличии мультиколлинеар-ности в страховых данных. Особенности применения различных методов проиллюстрированы на примере с использованием реальной страховой статинстики.

7. Новые методы прогнозирования ожидаемых нетто-премий на осннове оценок Джеймса - Стейна.

Полвека назад У. Джеймс и К. Стейн (Proceedings of the Forth Berkley Symposium. Vol. 1. Berkley: University of California Press, 1961. P. 361-379) нашли смещенную оценку, которая была равномерно лучшей (с точки зрения квадратичного критерия), чем обычно рекомендуемая наилучшая несмещеннная оценка. На этой основе выросло направление математической статистики по разработке и использованию оценок специального вида, которые (как и традиционные актуарные оценки) можно интерпретировать как компромисс между альтернативными подходами. Статистическая литература по данному направлению содержит более разработанный (по сравнению с актуарной) апнпарат, в т.ч. и для случаев с произвольными ковариационными матрицами.

Тем не менее, в рамках метода актуарных расчетов ранее не осуществнлялось попыток заимствовать оценки Джеймса - Стейна для их приложения к

27

решению страховых задач. В частности, никогда не проводилось исследованние условий, при которых они будут давать более точный прогноз страховых выплат, и, следовательно, служить более совершенной основой премий (танрифной системы).

Оценки Джеймса - Стейна можно рассматривать как альтернативные подходы к конструированию эмпирических байесовских оценок будущих вынплат, рассматриваемых в качестве основы прогнозирования размера страхонвой премии. Следует отметить, что актуарии выбрали свой подход, скорее иснходя из удобства интерпретации, чем из точности прогноза. Поэтому применнение оценок Джеймса - Стейна в целом повышает качество прогнозированния страховых выплат и размера премии.

Для выявления диапазонов применимости различные подходы сравнинвались между собой в рамках имитационного исследования, идея которого состояла в том, что рассматриваемые оценки должны выявить заранее известнные свойства сгенерированной совокупности данных и дать в целом лучший прогноз будущих выплат, чем традиционные актуарные подходы. В качестве критериев сравнения использовались мера близости по Питману и поведение доверительного интервала. Мера близости по Питману

Ре(51,52) = Рг[||51-0||2<||52-0||2] упорядочивает две оценки 5Х и 52: если Р0(51,52) больше одной второй, то оценка 5Х лучше, чем 52, т.к. 5Х чаще оказывается ближе к истинному значеннию 0.

Основой сравнения (т.е. свойствами, которыми должны были обладать данные, сгенерированные в рамках имитационного исследования) являются различные формы зависимости, выражаемые в ходе данного исследования для разных видов ковариационных матриц. В частности, рассматривались конвариационные матрицы S с (у'Д)-ми элементами Cov[X;y,X;fc], которые отранжают линейные зависимости между страховыми выплатами по одному и тому же i-му объекту (подпортфелю) в разные моменты времени, а также матрицы 12 с (i, /)-ми элементами Cov^y,^-], описывающие зависимость между разнличными объектами (подпотрфелями) в фиксированные моменты времени j. При этом также использовались такие ковариационные матрицы, которые встречаются на практике, но игнорируются традиционными актуарными поднходами.

28

В рамках сравнительного исследования различных подходов в качестве инструментов актуарного анализа на основе имитационного моделирования рассмотрены следующие оценки:

1. традиционная актуарная оценка 8f, с которой сопоставляются все оснтальные;
2. положительная версия оценки Линдли 6^аа на базе наилучшей эк-вивариантной оценки дисперсии;

ча тта SL/UMVU+г

1. положительная версия оценки Линдли 6^а на базе несмещенной эффективной оценки дисперсии;
2. положительная версия оценки Грина - Стродермана 6^а на базе наилучшей эквивариантной оценки дисперсии;

чаа SGS/UMVU+г

1. положительная версия оценки 1 рина - Стродермана 6^а на базе несмещенной эффективной оценки дисперсии;
2. оценка Эфрона - Морриса 8fM1;
3. положительная версия оценки Берри 8fer+;

h) положительная версия оценки Джеймса - Стейна 6^аа для произвольнной ковариационной матрицы;

i) положительная версия оценки Эфрона - Морриса sfM2+для произнвольной ковариационной матрицы;

j) положительная версия оценки Салеха - Сена 8fs+для альтернативной структуры зависимости;

к) положительная версия оценки Хадсона 6f+ для гамма-распределения;

1) оценка Морриса 6^ для гамма-распределения.

Сравнительные расчеты по указанным оценкам для данных, подчиненнных распределению Гумбеля, приведены в табл. 2. Распределение Гумбеля -классический пример распределения с тяжелыми хвостами и сильной асимнметрией, которое часто встречается в финансовой и страховой практике, но которое весьма далеко от предположений стандартных статистических и акнтуарных моделей. Кроме него в этом исследовании на основе имитационного моделирования были рассмотрены и другие типы распределений, для котонрых получены сходные результаты, что обеспечивает репрезентативность иснследования.

29

Таблица 2. Значения меры близости по Питману PQ(8A, 5) для альтернативных оценок типа Джеймса-Стейна

по отношению к традиционной актуарной оценке 8fна основе случайных величин, подчиненных распределению Гумбеля

	r~L/BSI+	r~L/UMVU+	r~GS/BSI+	r~GS/UMVU+	rгMl	?Ber+	8Г	сЯМ2 +	6f+	5f+	6f
" Ч 41а А Ч I	0,525	0,511	0,514	0,516	0,412	0,478	0,465*	0,292*	0,491	0,497	0,156
S = 1001П,П = \т	0,515	0,468	0,488	0,493	0,414	0,351	0,343	0,385	0,423	0,307	0,322
"-' = ^ln "Х" l'-'enen, 12 = lm	0,092	0,089	0,090	0,091	0,080	0,084	0,631	0,752	0,093	0,117	0,711
S = 100In + 10e^en. = Im	0,005	0,004	0,004	0,005	0,045	0,004	0,874	0,941	0,006	0,404	0,966
" э*паа 'аа ^^^п^п > ^' *т	0,046	0,044	0,044	0,044	0,047	0,041	0,749	0,851	0,047	0,151	0,787
S = 1001п + 400е?еп , ft = 1т	0,001	0,001	0,001	0,001	0,544	0,001	0,670	0,842	0,004	0,532	0,994
Е = 5[0.951*--'П..аа ,ft = Im L JiJ=l,...,n'аа т	0,179	0,177	0,177	0,177	0,156	0,173	0,651	0,607	0,173	0,700	0,660
Е = 100(0,95|*--'Т). . ,ft = Im ^ -'1,7 = 1,...,п '"	0,007	0,003	0,004	0,004	0,062	0,003	0,659	0,851	0,003	0,273	0,949
L Ji,7 = l,...,n'аа m	0,481	0,469	0,474	0,475	0,367	0,439	0,462	0,334	0,452	0,455	0,202
s = юоГо.о5^-^П.. ,ft = im L Ji,7=l,...,n'аа m	0,485	0,424	0,444	0,450	0,369	0,306	0,319	0,357	0,369	0,291	0,356
z = \n,a = io[o.9|i--'|l.. "а Lаа J i,7=l,. ...m	0,059	0,047	0,052	0,053	0,016	0,034	0,531	0,583	0,034	0,074	0,842
71'а Lаа H,j=l,...,m	0,711	0,679	0,690	0,691	0,676	0,636	0,555	0,455	0,618	0,633	0,676
" ^n ' ^' -'ж"^m "Х" -'-Х-'"m^m	0,989	0,987	0,988	0,988	0,960	0,975	0,613	0,283	0,981	0,982	0,000
S = In, ft = 100Im + 400e^em	0,851	0,823	0,836	0,839	0,773	0,770	0,647	0,631	0,774	0,759	0,796

Вероятность накрытия доверительным интервалом истинного значения меньше 95%.

Имитационное исследование показало, что во многих случаях альтернантивные оценки позволяют чаще получать более точный прогноз, чем традинционная актуарная оценка, особенно при наличии сложных форм зависимонсти. В частности, из табл. 2 видно, что при наличии достаточно сильной завинсимости (за исключением авторегрессионного типа с небольшой дисперсией) между договорами практически все альтернативные оценки лучше актуарной.

При наличии зависимости от времени почти всегда следует рекомендонвать оценку Морриса. Исключение из данной рекомендации представляют только случаи слабой зависимости, где актуарные методы работают лучше, но такие случаи как раз не характерны для страховой практики. Аналогичные результаты получены и для других видов распределений. На этой основе в работе даны соответствующие рекомендации по выбору типа оценки при разнной интенсивности зависимости и, если есть такая информация, о структуре ковариационной матрицы.

В целом, следует сделать вывод о том, что при выборе метода оценки страховой премии в актуарной практике необходимо проводить предваринтельное исследование структуры и степени зависимости либо иметь соответнствующую априорную информацию. Некоторые свойства распределения, ленжащего в основе данных, например, величина асимметрии, также могут сунщественно влиять на качество оценок. Наличие дополнительной информации позволяет выбрать более точный метод прогнозирования и повысить достонверность оценки страховых премий.

8. Применение метода квантильной регрессии для оценки нетто-премий.

Квантильная регрессия (и его частный случай - медианная регрессия) часто рассматривается как альтернатива традиционным регрессионным моденлям, основанным на методе наименьших квадратов, и обобщенным линейным моделям. В частности, метод наименьших квадратов имеет ряд существенных недостатков, в том числе чувствительность к выбросам, определенным тинпам зависимости (например, между коэффициентами регрессии и случайнынми ошибками) и т.п. В свою очередь, обобщенные линейные модели, котонрые, как правило, предполагают использование метода максимального правндоподобия, требуют априорного знания типа распределения страховых вынплат, чувствительны к зашумлению выборки, т.е. наличию неоднородности

в наблюдениях, и т.д.

31

Вместе с тем подобные сложности часто встречаются в страховой стантистике. В частности, среди таких нарушений можно, например, назвать:

1. неточность задания распределения, управляющего наблюдениями в выборке, так что предположения классических регрессионных моделей об однородности выборки или о достаточно красивом механизме проявления однородности не могут быть проверены;
2. наличие распределений с более тяжелыми хвостами, чем у нормальнного распределения, что вызывает необходимость выбора методов оцениванния, придающих меньшие веса крайним наблюдаемым значениям, или даже полного отказа от метода наименьших квадратов;
3. присутствие в выборке небольшой доли выбросов, то есть наблюндений, вызванных каким-либо шумом, отделить которые на основе апнриорной информации, как правило, невозможно. Это требует использованния процедур, мало чувствительных к таким засорениям выборки;
4. зависимость элементов выборки, которая имеет сложную структуру, так что ее трудно или даже невозможно выделить и/или анализировать (например, с помощью ковариационной матрицы).

Иными словами, в ряде практических задач, требующих применения регреснсионного подхода, классические регрессионные методы неработоспособны и не позволяют делать правильные выводы о характере исследуемого процесса возникновения страховых выплат и о требованиях к размеру страховой пренмии.

Квантильная регрессия не чувствительна к указанным недостаткам, т.е. демонстрирует неприхотливость к свойствам используемых данных. Это вынражается в независимости метода от функции распределения, робастном ханрактере оценок и отсутствии смещения. Кроме того, в ряде случаев доверинтельные интервалы для оценок квантильнои регрессии уже по сравнению с оценками классических методов.

Поэтому применение метода квантильнои регрессии в актуарной пракнтике позволяет получать более точные прогнозы будущих выплат, а следовантельно, и более адекватную оценку страховых премий. Иными словами, принменение данного метода имеет ряд существенных преимуществ, связанных со свойствами страховой статистики.

Кроме того, применение квантилей распределения лучше согласуется с целями оценки нетто-премии, т.к. позволяет одновременно оценить не только

32

ожидаемую нетто-премию, но и рисковую надбавку. При использовании трандиционных регрессионных подходов актуарии вынуждены использовать разнличные методы оценки указанных компонентов страховой премии. Это тренбует дополнительного согласования как самих методов, так и полученных на их основе оценок. Метод квантильной регрессии позволяет избежать данных сложностей, что дает дополнительные возможности для прогнозирования страховых премий и повышения точности такого прогноза.

Для выявления диапазона применимости различных методов было пронведено исследование на базе имитационного моделирования. Оно было оснонвано на использовании наборов сгенерированных данных с известными свойнствами. В частности, рассматривались смеси хороших и плохих объекнтов, помеченных соответствующим индикатором, так что регрессионная мондель должна была расщепить соответствующую смесь и предсказать значение третьего квартиля (0,75 квантили). Сравнение различных подходов проводинлось по точности прогноза указанного квартиля. Эти смеси сильно отличанлись прежде всего использованными распределениями, хотя первые два монмента распределений совпадали. Основные характеристики сгенерированных данных приведены в табл. 3.

Расчеты осуществлялись тремя регрессионными методами. В силу того, что характеристики генерируемых наборов данных известны, различия в пронгнозах связаны с качеством указанных методов. Результаты расчетов преднставлены на рис. 3.

Результаты имитационного моделирования подтверждают тот факт, что в тех ситуациях, которые хорошо согласованы с классическими моделями линнейной регрессии и обобщенными линейными моделями, метод квантильной регрессии дает сопоставимые по качеству оценки. Вне этой области примененния (сильная асимметрия и тяжелые хвосты) классическая линейная регреснсия на основе наименьших квадратов и обобщенные линейные модели дают заведомо неправильную оценку, в частности для данных с тяжелыми хвостанми и остаточной неоднородностью, т.е. для ситуаций, часто встречающихся на практике, квантильная регрессия обеспечивает более точный прогноз.

Иными словами, метод квантильной регрессии во всех ситуациях понзволяет получить более точную оценку нетто-премии по сравнению с метондами, традиционно используемыми актуариями.

33

Таблица 3. Основные характеристики сгенерированных данных

Тип объекта	Распределение, лежащее в основе наборов данных	Математическое ожидание	Стандартное отклонение	Третий квартиль
хороншие	Нормальное	300,0	150,0	401,17
	Гамма с небольшой дисперсией	300,0	150,0	383,21
	Гамма с большой дисперсией	300,0	375,0	409,34
	Смесь распределений с тяжелым хвостом	300,0	375,0	643,51
плохие	Нормальное	450,0	150,0	551,17
	Гамма с небольшой дисперсией	450,0	150,0	540,12
	Гамма с большой дисперсией	450,0	382,0	618,50
	Смесь распределений с тяжелым хвостом	450,0	382,0	873,35

1. Экономико-математические и статистические актуарные модели оценки страховых премий должны учитывать следующие особенности страховой статистики - неоднородность данных, их ограниченность и наличие различнных форм связи между ними.
2. В качестве инструмента оценки страховых премий модели оценивания с учетом качества данных развиваются достаточно давно. Они хорошо приспонсоблены к построению оценок, характеризующихся ограниченностью объема данных и их неоднородностью. Однако диапазон применения таких оценок недостаточно широк. Это обусловлено использованием в моделях предполонжений об относительно простых формах зависимости используемых данных, что на практике реализуется достаточно редко.
3. Экономико-математические и статистические актуарные модели оценки страховых премий должны учитывать факторы страхового риска, при этом отбор таких факторов также является самостоятельной задачей.
4. В страховой практике встречаются разнообразные типы и формы завинсимости между наблюдаемыми данными о прошлых страховых выплатах и факторами риска. Учет этих форм зависимости позволит существенно повынсить адекватность моделей оценки страховых премий и точность прогнозиронвания последних. Однако учет других дополнительных особенностей страхонвой статистики (прежде всего, ограниченности ее объема) существенно уснложняет модели оценки страховых премий.
5. При исследовании влияния факторов риска на страховые выплаты актуанрии часто сталкиваются с мультиколлинеарностью между наблюдаемыми факторами. Традиционные регрессионные модели с учетом качества данных в подобных ситуациях не позволяют получать оценки, т.к. они работают только для матриц с полным рангом, что сужает область применения таких моделей в актуарной практике. Методы, нечувствительные к мультиколлинеарности, станут более универсальным инструментом анализа.
6. Как инструмент прогнозирования страховых премий могут использонваться оценки Джеймса - Стейна, применяемые в математической статистике. Однако, прямое их применение в страховой практике невозможно в силу того, что предполагает использование ряда предпосылок, зачастую не соблюдаенмых в практике страховании. При этом трудно оценить даже порядок ошибки, обусловленный нарушением этих предпосылок. Зачастую становится невознможной и интерпретация результатов, полученных при использовании оценок

36

Джеймса - Стейна.а Сказанное означает обязательность изучения области применения этих оценок в страховой практике как самостоятельной.

Х В качестве метода оценивания нетто-премии традиционные регрессионнные подходы (метод наименьших квадратов и метод обобщенных линейных моделей) обладают рядом существенных недостатков. Прежде всего, необхондимо выполнение соответствующих предпосылок, которые на практике часто нарушаются. При этом трудно оценить порядок ошибки, связанный с таким нарушением. Кроме того, имеются и содержательные сложности приложения результатов расчетов к практическим ситуациям.

Все указанные выше недостатки применения традиционных актуарных методов определяют необходимость разработки новых моделей оценки странховых премий, повышающих точность прогноза. В ходе проведения исследонвания получены важные научные результаты:

1. Показана ведущая роль экономико-математических актуарных методов оценки страховых премий в процедурах научного обоснования и принятия решений об их размере, т.к. именно на их основе увязывается страховой риск с прогнозами будущих выплат, а следовательно, стоимости страховых услуг. По мере развития методов актуарного анализа возрастает роль экономико-математических моделей прогнозирования страховых премий в процессах принятия решений в страховых организациях;
2. Раскрыты особенности статистики страховых выплат, играющие ключенвую роль при оценке премий (неоднородность рисков, ограниченность объенма информации и наличие сложных форм зависимости в статистических даннных). Они должны учитываться при построении соответствующих экономинко-математических моделей в целях повышения точности прогноза размера премии, хотя для актуарных методов, традиционно используемых для оценки премий до настоящего времени, не все из них принимаются во внимание. В результате показано, что для некоторых ситуаций, встречающихся в страхонвой практике, эти методы неприменимы, так что выявлены границы и осонбенности применения традиционных актуарных методов прогнозирования размера страховых премий на основе оценки с учетом качества данных. В этой связи продемонстрирована необходимость разработки новых моделей такого типа;
3. Вскрыты различные механизмы влияния характеристик риска на размер страховых выплат и, соответственно, на размер страховых премий по заклю-

37

чаемым договорам. Показано, что прямой механизм влияния игнорировался традиционными методами оценки премий, используемыми актуариями до нанстоящего времени. На этой основе предложены новые методы, учитывающие данный механизм;

1. Показано, что важную роль для формы оценки размера страховой пренмии (вида формулы прогноза) играет влияние характеристик риска, не имеюнщих количественного выражения, на наблюдаемые данные о выплатах, но не формы зависимости между этими факторами. Данный результат означает, что соответствующие предпосылки о зависимости между факторами риска можно считать несущественными и исходить из относительно простых соотношенний, что упрощает постановки экономико-математических моделей;
2. Получена оценка ожидаемой нетто-премии для ковариационной матрицы со специфической гребневой структурой для данных о страховых выплатах. Построенная модель является обобщением актуарных моделей Бюльманна и Бюльманна - Штрауба и может быть использована на практике для более шинрокого набора типов зависимости в исходных данных;
3. Модифицированы традиционные регрессионные подходы к оценке странховых премий, чтобы обеспечить их нечувствительность к мультиколлинеар-ности факторов риска. В частности, использованы такие подходы, как перенход к главным компонентам, гребневая регрессия и решение недоопределен-ной системы нормальных уравнений. Эти подходы определяют новые методы оценивания страховых премий с учетом качества данных. С точки зрения уснловий применимости решение недоопределенной системы нормальных уравннений представляется наиболее гибким подходом;
4. Предложено использовать в качестве инструмента прогнозирования страховых премий оценки Джеймса - Стейна, используемые в математиченской статистике. Хотя традиционные актуарные методы можно рассматривать как частный случай таких оценок, предложенный метод обеспечивает более точные прогнозы из-за учета структуры ковариационной матрицы, что поднтверждается результатами имитационного моделирования. Сформулированы практические рекомендации по выбору соответствующих оценок в различных практических ситуациях;
5. Рассмотрены возможности и условия применения метода квантильной регрессии для оценки страховой премии, который позволяет преодолеть нендостатки классических регрессионных методов, используемых актуариями.

38

Среди преимуществ метода квантильной регрессии можно отметить его ненвысокую требовательность к используемым данным. Это выражается в незанвисимости метода от функции распределения, робастном характере оценок и отсутствии смещения. Особую важность имеет тот факт, что предложенный метод обеспечивает хорошую экономическую интрепретацию, позволяя оценнивать нетто-премию в целом (рисковая надбавка и ожидаемая нетто-премия оцениваются одновременно), что повышает адекватность полученных резульнтатов.

IV. НАУЧНЫЕ ПУБЛИКАЦИИ

Основные положения диссертации отражены в следующих опубликованных научных работах:

I. Публикации в журналах из списка ВАК

1. Кудрявцев А.А. Регрессионная модель прогнозирования с учетом канчества данных // Вестник Инжэкона. Серия Экономика. 2006. № 4 (13). С. 159-163. (0,45 п.л.)
2. Кудрявцев А.А. Концепции финансового прогнозирования страховых компаний // Финансы и бизнес. 2006. №4. С. 74-79. (0,4 п.л.)
3. Кудрявцев А.А., Абдураманов Р.А. Особенности применения метода квантильной регрессии для оценки нетто-премии по страховым договорам // Вестник Инжэкона. Серия Экономика. 2008. Вып. 1. С. 182-190. (1,05 п.л.)
4. Абдураманов Р.А., Кудрявцев А.А. Анализ убыточности по договонрам ОСАГО методом медианной регрессии // Финансы и бизнес. 2008. №2. С. 131-142. (0,77 п.л.)
5. Кудрявцев А.А. Модель выбора инвестиционного портфеля на основе квантильных мер риска // Вестник СПбГУ. Сер. Экономика. 2008. Вып. 4. С.95-102. (0,61 п.л.)
6. Кудрявцев А.А. Развитие концепции актуарного анализа // Вестник СПбГУ. Серия 5 Экономика. 2009. Вып. 3. С. 134-147. (1,0 п.л.)
7. Кудрявцев А.А. Оценки Джеймса - Стейна в ценообразовании странховых продуктов // Вестник Инжэкона. Серия Экономика. 2010. Вып. 2 (37). С. 171-187. (1,25 п.л.)

39

1. Кудрявцев А.А. Регрессионные модели с учетом качества данных при наличии мультиколлинеарности // Вестник Инжэкона. 2010. Вып. 5 (40). С. 146-154. (0,75 п.л.)
2. Кудрявцев А.А. Модели Бюльманна и Бюльманна-Штрауба с альтерннативной структурой зависимости // Вестник СПбГУ. Сер. 5. Экономика.

2010. Вып. 4. С. 76-87. (0,75 п.л.)

1. Кудрявцев А.А. Основные подходы к ценообразованию (тарификанции) в страховании // Финансы и бизнес. 2011. №1. С.39-52. (1,15 п.л.)
2. Кудрявцев А.А. Иерархическая модель оценки страховых премий с учетом качества данных со структурой зависимости, порожденной общими эффектами (случай нормальных распределений) // Вестник Инжэкона. 2011. Вып. 2 (45). С. 186-193. (0,55 п.л.)
3. Кудрявцев А.А. Особенности оценки страховых премий, обусловнленные спецификой имеющейся страховой статистики // Финансы и бизнес.

2011. №3. С. 68-73 (0,55 п.л.)

IIПубликации в иностранных реферируемых журналах, приравненных к журналам из списка ВАК

13. Kudryavtsev A.A. Using quantile regression for rate-making // Insurance:

Mathematics and Economics. 2009. Vol. 45. N. 2. P. 296-304. [Использование

квантильной регрессии для оценки премий] (1,2 п.л.)

III. Монографии

1. Кудрявцев А.А. Менеджмент в здравоохранении: медико-экононмические стандарты и методы их анализа. СПб.: Изд-во СПбГУ, 2004. (к теме диссертации имеют отношение п. 4.2.2 и п.5.2.3 монографии общим объемом 2,7 п.л. из 10,0 п.л.)
2. Кудрявцев А.А. Методология актуарного анализа. СПб.: Изд-во СПбГУ, 2009. 204 с. (к теме диссертации имеют отношение главы 1 и 2, а также з3.1 и з4.1 монографии общим объемом 4,26 п.л. из 10,86 п.л.)
3. Кудрявцев А.А. Экономико-математические модели актуарной оценки страховых премий по данным из малых выборок при различных форнмах зависимости. СПб.: Нестор-История, 2011. 216 с. (13,5 п.л.)

40

IV. Статьи в прочих научных изданиях

1. Кудрявцев А.А. Основные направления разработки типовых метондик обоснования операций обязательного медицинского страхования // Пронблемы перехода к рыночной экономике и опыт зарубежных стран: Сб. научнных работ. Вып. IV. М.: МО РНФ, 1996. С. 82-97. (1,0 п.л.)
2. Поляков И.В., Кудрявцев А.А. Задачи актуарных расчетов по мединцинскому страхованию // Бюллетень С.-Петербургского института медициннского страхования. Вып. 2. СПб., 1996. С.68-76. (0,4 п.л.)
3. Поляков И.В., Кудрявцев А.А. Особенности актуарных расчетов для добровольного медицинского страхования // Проблемы социальной гигиены и история медицины. 1996. № 4. С. 23-41. (0,4 п.л.)
4. Чернова Г.В., Поляков И.В., Кудрявцев А.А. Принципы андеррайнтинга в медицинском страховании // Медицинское страхование. 1997. № 16. С. 34-37. (0,4 п.л.)
5. Erohin I.V., Kudryavtsev А.А. On links between the different definitions of time in IBNR run-off triangles // 11th International Congress "Insurance: Maнthematics and Economics" July 10-12, 2007, Piraeus, Greece. Book of Abstracts. P. 53. [О связи между различными определениями времени и РПНУ] (0,1 п.л.)
6. Abduramanov R., Kudryavtsev A. The method of quantile regression, a new approach to actuarial mathematics // 11th International Congress "Insurance: Mathematics and Economics" July 10-12, 2007, Piraeus, Greece. Book of Abstracts. P. 56-57. [Метод квантильной регрессии, новый подход в актуарной математике] (0,1 п.л.)
7. Кудрявцев А.А. Страницы истории развития актуарного анализа. // Рынок страхования. 2008. №1. С. 22-26. (0,45 п.л.)
8. Кудрявцев А.А., Абдураманов Р.А. Прогнозирование убыточности по договорам ОСАГО с помощью авторегрессионной модели на основе мединанной регрессии. В кн.: Современная система мирохозяйственных связей: тенденции развития и перспективы. СПб.: Европейский дом, 2008. С. 347-366. (1,25 п.л.)
9. Кудрявцев А.А. Применение оценок Джеймса-Стейна в страховой математике // Обозрение прикладной и промышленной математики. 2009. Т.16.Вып.2. С.359. (0,1 п.л.)
10. Kudryavtsev A. Credibility and James-Stein Estimators. In: XHIth Interнnational Congress on Insurance: Mathematics and Economics (IME2009). May 27-

41

29, 2009. Istanbul, Turkey. Programme and Submitted Abstract Book. P. 60. [Оценки с учетом качества данных и оценки Джеймса - Стейна] (0,1 п.л.)

1. Kudryavtsev A. Credibility regression models with multicollinear or near-multicollinear data. In: 14th International Congress on Insurance: Mathematнics and Economics. June 17-19, 2010. Toronto. Canada. Abstracts. P. 51. [Регреснсионные модели с учетом качества данных при наличии мультиколлинеарно-сти] (0,1 п.л.)
2. Кудрявцев А.А. Функции страховщика. В кн.: Страхование: экононмика, организация, управление. В 2-х т. / Под ред. Г.В. Черновой. T.l. М.: Экономика, 2010. С. 155-183. (1,75 п.л.)
3. Кудрявцев А.А. Сравнение оценок с ограниченной флуктуацией и оценок с наибольшей точностью в теории доверительного оценивания // Акнтуарий. 2010. №1. С. 43-47. (0,6 п.л.)
4. Кудрявцев А.А. Методика оценки премий в условиях мультиколли-неарности. В кн.: Модернизация экономики: проблемы и перспективы. Матенриалы международной научной конференции, посвященной 70-летию со дня основания Экономического факультета СПбГУ. 14-15 октября 2010 г. Секции 7-13. СПб: ЭФ СПбГУ, 2010. С. 139. (0,1 п.л.)

42

     Авторефераты по всем темам  >>  Авторефераты по экономике