Все авторефераты докторских диссертаций

Развитие теории и разработка вибрационных электромеханических систем сельскохозяйственного назначения

Автореферат докторской диссертации

На правах рукописи

Денисов Валерий Николаевич

аРАЗВИТИЕ ТЕОРИИ И РАЗРАБОТКА ааВИБРАЦИОННЫХ аЭЛЕКТРОМЕХАНИЧЕСКИХаа аСИСТЕМа СЕЛЬСКОХОЗЯЙСТВЕННОГОаа аНАЗНАЧЕНИЯа а

Специальность: 05.20.02 - электротехнологии и электрооборудование в сельском хозяйстве

Автореферат адиссертации на соискание ученой степени доктора

технических наук

Москва - 2012

Работа выполнена в Федеральном государственном бюджетном образовательном учрежденииа высшего профессионального образования л Российский государственный аграрный заочный университет. а

Научный консультант:аа Мамедов Фуад Алиевичаа доктор технических наук, профессор.

Официальные оппоненты:

Беспалов Виктор Яковлевич, д.т.н., апрофессор, Федеральное государственное бюджетное образовательное учреждениеа высшего профессионального образования Национальный исследовательский университет МЭИ, профессор кафедры Электромеханика;

Гольдберг Оскар Давидович, д.т.н., профессор, Федеральное государственное бюджетное образовательное учреждениеа высшего профессионального образованияа л Московский государственный открытый университет им. В.С.Черномырдина, заведующий кафедрой Электрических машин;

Забудский Евгений Иванович,а д. т. н., профессор, Федеральное государственное бюджетное образовательное учреждениеа высшего профессионального образования л Московский государственный агроинженерный университет аим. В.П.Горячкина, апрофессор кафедры Электроснабжения и электрических машин.

Ведущая организация: Государственное научное учреждениеаа Всероссийский научно-исследовательский института электрификациии сельского хозяйства Российской академии сельскохозяйственных наук.

Защита состоится л_29__а _мая____ 2012__ г. в __ часов ___ минут

на заседании диссертационного совета Да 220.056.03 апри Федеральном государственном бюджетном образовательном учрежденииа высшего профессионального образования л Российский государственный аграрный азаочный ауниверситет апо адресу: аа143900, аМосковская область, аг. Балашиха 8, ул. Ю. Фучика, д. 1.

С диссертацией можно ознакомиться в библиотеке Федерального государственного бюджетного образовательного учрежденияа высшего профессионального образования л Российский государственный аграрный азаочный ауниверситет.

Автореферат разослан ___ ______201___ г.

Ученый секретарь диссертационного света

к.т.н, доцент _______________________________________(О.П.Мохова)___

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

аа Актуальность проблемы. аСодержанием современного этапа развития АПК является переход от экстенсивного к интенсивному пути развития. Аграрное производство РФ все ещеа сохраняет черты экстенсивной системы.а Оноа в 5 раз более энергоемко, в 4 раза более металлоемко, а производительность труда ав 10 - 13 раз ниже, чем в США. Переход к интенсивному пути развития требует инновационных решений в отношении электрооборудования и технологий АПК, а также амодернизации существующей техники. На это анеоднократно указывалось в ряде директивных документов: Перечне приоритетных направлений развития науки, технологий и техники Российской Федерации, аПеречне критических технологий Российской Федерации. Это отмечается и ав Государственной программеа развития сельского хозяйства и регулирования рынков сельскохозяйственной продукции, сырья и продовольствия на 2008..2012 годы. В материалах и рекомендациях Министерства сельского хозяйства и Россельхозакадемии большое внимание уделяетсяа повышению технического уровня сельскохозяйственной техники путем её модернизации. По существующим оценкам модернизация аатехнологических машин (ТМ) аадаст экономический эффект в сотни миллионов рублей. а Намечены два направления интенсификации производства продукции в АПК; разработка новой техники и модернизация существующей. Качественное изменение ситуации ав этих направлениях невозможно без аразвития научного обоснования разработок и модернизации сельскохозяйственной техники.а Большинство ТМ,а эксплуатирующихся в настоящее время, аобладают повышенным энергопотреблением и избыточной материалоемкостью. Причинами этого являются:аа а аа1.Использование несовершенных кинематических схем электропривода;аа 2.Морально и физически устаревший парк электрооборудования; аа3.Несовершенство технологических процессов и рабочих органов (РО) ТМ;а аа4.Недостаточное использование устройств регулирования характеристик электропривода с учетом изменения их в процессе работы. Одним из ключевых направлений арешения отмеченных выше проблем являетсяаа совершенствование применяемыха в АПК вибрационных ТМ, представляющих собой вибрационные электромеханические системы (ВиЭМС).а Ведь в 63% технологических процессов АПК источником вибрации являются инерционные дебалансные вибраторы, приводимые в движение в 71% случаев от асинхронных электродвигателейа а Рабочие органы ВиЭМСа совершаюта движения, получаемые в результате композиции элементарных продольных перемещений по трем осям координат. Для реализации продольных перемещенийа РО использование линейных асинхронных двигателей (ЛАД) в ВиЭМС наиболее рационально. Это позволяет устранить акинематические энергопоглощающие устройства и снизить материалоемкость конструкции.а Применение ВиЭМСа с рекуперацией электрической энергииа и управлением работой ЛАД создает условия для повышенияа энергетических показателей. аЛАД с рекуперацией энергии иа управлением, вследствиеа простоты изготовления, монтажа, обслуживания, использования вторичного элементаа ЛАД как РО ТМ, позволяют совершенствовать ВиЭМС для АПК. аОднако,а в силу большого разнообразия конструкций, малосерийного изготовления,а отсутствия опыта проектирования и эксплуатации ЛАД, адля создания энергоэффективных ВиЭМС на их основе аатребуются научно обоснованные математические модели, обеспечивающие возможность многократных расчетов различных вариантов конструкций и нагрузок.

Перспективным направлением снижения материалоемкости ТМ являетсяа совершенствование рабочих органов аТМ за счет уменьшения избыточного запаса прочности. В связи с недостаточной научной и методической проработкой вопросов проектирования вибрирующих рабочих органов ВиЭМС,а в эти системы закладывают 2-3 кратный запас прочности, реализуемый избыточным объемом металлоконструкций. Это обусловленоа опасениями вибрационного разрушения привода и рабочего органа. Кроме того,а при создании ВиЭМС, апрактически не исследованными остаются вопросы взаимодействия рабочих органов со средой. При проектированииа РО ВиЭМС малоа используютсяа резонансные аи нелинейные эффекты. Назрел вопрос о разработке методов исследований нелинейных колебаний РО аресурсосберегающих ТМ с учетом их работы в сыпучей среде.аа аа Взаимодействие электрических и механических подсистем в ВиЭМСа является неотъемлемой частью вибротехнологических процессоваа в машинах и аппаратах АПК.а Выработка анаучно обоснованных методов исследования взаимодействия таких подсистем позволяет найти подходы к улучшениюа характеристик энергопотребления. Дляа получения конструкций ВиЭМС, позволяющих решать поставленные выше задачи, авыработки рекомендаций поа аих проектированию иа использованию,а необходимы научно обоснованные методы аамоделированияаа как работы составных частей в отдельности, так и асовместной работы этих частей.а Рабочие органы ТМ в сельском хозяйствеа используютсяаа в широкома диапазоне амплитуд и частот, зачастую при неизменных параметрах колебаний. Это приводит ка аснижению эффективности работы этих машин и качества выпускаемой продукции, так как в действительности эти параметры должны изменяться в процессе работы в зависимости от особенностейа технологического процесса.а Требуется дальнейшая модернизация ВиЭМС аАПКа с учетом возможности оперативного изменения параметров колебаний ав ходе технологического процесса. аа ЛАД, используемый в приводе ВиЭМС, является несимметричной электрической машиной (ЭМ). В условиях сельского хозяйства,а ВиЭМС работает как часть несимметричной энергетической системы. Повышение энергоэффективности ВиЭМС невозможно без развитияа теории энергетических процессов в несимметричных энергетических объектах. Для решения задач, возникающих на пути повышения энергоэффективности ВиЭМС, необходимоа совершенствование научного обоснования энергетических процессов ва ЛАД и несимметричных энергетических системах с учетома неоднородности характеристик этих объектов. а аа Имеются следующие пути повышения энергоэффективности и снижения материалоемкостиа ВиЭМС: аа аа1. Применение упрощенных кинематических схем электропривода в теха случаях, когда это целесообразно, технически осуществимо и экономически оправдано. Эта мера позволяет не только экономить электрическую энергию, но и существенно снижать материалоемкость ТМ;аа аа2. Созданиеа математических моделейа ЛАД для ВиЭМС, обладающих свойствами системности, универсальности и возможностями численно-аналитического исследования, как основы для разработки энергоэффективных и ресурсосберегающих аВиЭМС; аа

3. Создание системы диагностики ВиЭМС, как инструмента поддержания его высоких технических и энергетических характеристик; а аа4. Совершенствование РО ВиЭМС с учетом их продольно-поперечных колебанийа в сыпучей среде на основе атеории нелинейных колебаний;аа 5.Разработка и реализация аконцепции рационального питанияа несимметричных ВиЭМС.а аа В диссертационной работе впервые рассматриваются, представляющиеа актуальную научно-техническую проблему, имеющие важное народно хозяйственное значение,а вопросыа научного обоснования аматематических моделей ЛАД ас рекуперацией энергии, амплитудно-частотных зависимостей для рабочих органов ТМ, совершающих колебания в сыпучей среде, энергетических процессов, происходящих в электрических машинах (ЭМ) и несимметричных энергетических системах, а также модернизированные энергоэффективные ТМ для АПК. аа аЦель диссертационной работы. Диссертационная работа направлена на развитие научных основ разработкиа и аамодернизации аресурсосберегающих, аэнергоэффективных вибрационных электромеханических систем для АПК с продольно-поперечными движениями рабочих органов.аа В соответствии с целью диссертационной работы были поставленыаа следующие задачи:

аРазработка универсальныха аинженерных математических моделей ВиЭМС на базеаа ЛАД;
Исследование и сравнительный анализ разных типов ЛАД для ВиЭМС;
Экспериментальная проверка адекватности аразработанных математических моделей;
Развитие методов расчетаа колебаний рабочих органов ТМа при продольно-поперечных перемещениях в асыпучей среде;
Разработка численно-аналитической математической модели для нелинейных ВиЭМС;
Разработка научных основ многопараметрической диагностики аВиЭМС;
Развитие энергетической теории параметрически неоднородных система и методова визуализации энергетических процессов в них;
Модернизация и разработка ВиЭМС на базе ЛАД с рекуперацией энергии для АПК.

аа Объект исследований. Вибрационные электромеханические системы с продольно-поперечными движениями рабочих органов, использующие ЛАД, в частностиа ТМ аАПК, служащие для апосева, сушки, атранспортировки, апереработки продукции. аа аа а аа Предмет исследований. Математические модели ВиЭМС на базе ЛАД, собственные колебания РО ВиЭМС с учетом влияния среды, энергетические процессы в несимметричных ВиЭМС.а аа Методы исследования. Основные результаты диссертационной работы получены на основании фундаментальных законов и уравнений электромеханик, механики, теории интегральных уравнений и вариационного исчисления.аа Достоверность результатов исследований и выводов проверялась экспериментальными и численно-аналитическими методами, сравнениема полученных результатов с решениями других авторов, экспертизой разработанных технических решений в Роспатенте РФ.

Научные результаты , выносимые автором на защиту:

Универсальные аматематические модели ВиЭМС на базе ЛАД;
Результаты параметрических исследований на основе математических моделей;
Оценка энергетической эффективности ВиЭМС ас рекуперацией энергии и разночастотным аапитанием;
Амплитудно - частотные характеристики рабочих органов сельскохозяйственных машин апри больших прогибах с учетом параметров среды;
Научное обоснование способа диагностики ВиЭМС;
Энергетическая теория и визуальные модели энергетических процессов в параметрическиа неоднородных системах, имеющих место в АПК;

а Научная новизна работы состоит в следующем.

Развита итерационная схема нахождения решения полевого уравнения адля ЛАД;
Разработаны математические модели ВиЭМС, ориентированные на инженерную практику;
Проведен сравнительный анализ ЛАД с рекуперацией энергии и с разночастотным питанием и выработаныа рекомендации по их применению в сельском хозяйстве;
Впервые асимптотический метод В.В.Болотина (АМБ) применен для исследования собственных частот, амплитудно-частотных характеристик арабочих органов сельскохозяйственных машин в сыпучей среде;
Разработан математический аппарат для анализа нелинейныха ВиЭМС;
Научно обоснован новый способ диагностики аВиЭМС;
Впервые предложены визуальные модели энергетических процессов в ЭМ и введены понятия d и q подмножеств токов ЭМ.

Практическая ценностьа предлагаемой диссертационной работы заключаетсяаа в следующем:

аРазработке амоделей ЛАД, ориентированных на среду специалистов;
Упрощении кинематических схем, уменьшенииаа материалоемкости, повышении качественных характеристик аряда ВиЭМС, эксплуатируемых в АПК;
Возможности проводить параметрическое исследование процессов ва ВиЭМС на основе полученных аналитических приближений;
Получении аналитических выражений амплитудно-частотных характеристикаа рабочих органов аВиЭМС с учетом влияния асреды ;
аРазработке способа диагностики ВиЭМС.
Разработке новых, защищенных патентами РФ, ВиЭМС сельскохозяйственного назначении (сеялки, сушилки, смесители) с улучшенными характеристиками.

Реализация результатов диссертационной работы. аОсновные результаты диссертации использованы при выполнении госбюджетных НИР, проводимых в ФГБОУ ВПО л Российский государственный аграрный заочный университет по теме Разработка научного обеспечения и обоснования требований по повышению эффективности технологических машин АПК со встроенными электродвигателями и в рамках договора о научном сотрудничестве со Смоленским НИИ сельского хозяйства аРоссельхозакадемии. Результаты работы использованы концерном Русэлпром апри создании энергоэффективных двигателей серии 7AVE и энергонасыщенных тракторова Беларус-3023. Используются ааОАО Амкодор республики Беларусьа при модернизации зерноочистительно-сушильных комплексов ЗСК-40Ш. Внедреныа в учебный процесса в афилиале ФГБОУ ВПО НИУ МЭИ в г. Смоленске и в ФГБОУ ВПО л Российский государственный аграрный заочный университет г.Балашихи Московскойа области.

Апробация работы. Основные положения и результаты диссертации докладывались и обсуждались на научно-технических конференциях, школах и симпозиумах: Всесоюзной школе поа актуальным проблемама механики оболочек( Казань,КАИ,1983), IVа Международной конференции Электротехника, электромеханика и электротехнологии(18 - 22 сентября 2000. Россия, Клязьма), 5-й Международной. конференции. МКЭЭЭ(Крым, Алушта, 2003),а 4-м и 5-м международных симпозиумах ЭЛМАШ - 2002, ЭЛМАШ - 2004 (Москва), научно-технических конференциях РГАЗУ (Москва, 2006 - 2009 гг.), международной научно-технической конференции Электромеханические преобразователи энергии (Томск,2005 г.), Всероссийской научно-технической конференции с международным участием Актуальные проблемы энергосберегающих электротехнологий (Екатеринбург: ГОУВПО УГТУ - УПИ, 2006), VI Всероссийской научно-технической конференции Информационные технологии в электротехнике и электроэнергетике (Чебоксары, 2006 г.), XI-й, XII, XIII Международных конференциях л Электромеханика, электротехнологии, электротехнические материалы и компоненты( 2006 г., 2008 г., 2010 г., Крым, Алушта), V всероссийской научно-технической конференции Информационные системы и модели в научных исследованиях, промышленности и экологии, (Тула, 2006), Всероссийской научно-технической конференции Приоритетные направления развития науки и технологий (Тула,2006), VII Всероссийской .научно-технической конференции Динамика нелинейных дискретных электротехнических и электронных систем (Чебоксары, 2007), 6-й, 7-йа Международных научно-техническиха конференциях Энергообеспечение и энергосбережение в сельском хозяйстве ( 2008 г, 2010г., аМосква, ГНУ ВИЭСХ), ХХI, XXII Международныха научныха конференциях л Математические методы в технике и технологиях.- ММТТ-21 (Саратов, а2008), ММТТ-22 (Псков, 2009), XXVII Российской школе л Наука и технологии ( Екатеринбург, УрО РАН, 2008), Международной научно-практической конференции Обеспечение и рациональное использование энергетических и водных ресурсов в АПК (Балашиха, РГАЗУ, 2009), Межд. Научн.-техн. конференции. Энергетика, информатика, инновации -2011 ( Смоленск,2011).

Публикации. Содержание работы отражено ва 1 монографии, 1 учебном пособии с грифом УМО иа научных публикациях. В их числеаа 14 статей в ведущих рецензируемых научных журналах,а 31аа публикация в материалах конференций, совещаний и симпозиумов, имевших статус всероссийских и международных,а 12 патентов на изобретения и полезные модели.

Структура и объем работы. Диссертация состоит из введения, семи глав, заключения, списка литературы из 290 наименований и приложения, изложена наа 350 страницах амашинописного текста.

Основное содержание работы

Во введении обоснована актуальность работы, сформулирована аее цель, осуществлена постановка задач, приведены основные результаты работы, выносимые на защиту, аданные о ее новизне,а практической ценность, публикациях и структуре диссертации.

В первой главеа приводится обзор современного состояния аи аобластейа применения вибрационных технологий в основных отраслях сельского хозяйства.

Проанализированоа большое число работ в направлении уменьшения энергозатрата при использовании вибраций в области почвообработки. Отмечен вклад М.М. Крылова, А.Г Вульфа, Д.Д.Баркана, Н.С.Шкуренко, Г.Г.Трапезонцева, О.В.Верняева, В.И. Ускова, Л.В. Александряна, Р. Мюллера, А. Газеллы, А.И.Тарана,а А.Г Демьянченко и др. в аэтом направлении.

. В этих работах отмечается влияние вибраций на уменьшение тягового сопротивления плугов от 20% до 35%, снижение залипания рабочих органов, улучшение водно-воздушного режима, вспушивания, скважности и проницаемости почвы. Зафиксированы преимущества электропривода для задания движений рабочих органов ТМ,а где нужно менять частоту вращений или колебаний рабочих органов. Отмечено, что рассредоточенные электродвигатели, непосредственно передающие движения рабочим органам,а позволяют увеличить КПДа механизмов, уменьшить их материалоемкость, улучшить качественные характеристики за счет внедрения микропроцессорной техники.

Проанализировано применение вибрационных технологий ав растениеводстве. В работах В.М.Булгакова,а В.В. Брея,аа А.А.Василенко, П.М.Василенко, А.Г.Возмилова, Б.А.Волика, Н.П.Волоха, В.И.Гиммерфельда, В.И.Горшенина, ааБ.В.Зонова, Н.М. Зуева. Заложеныа основыа проектирования, теории и практики вибрационных технологий при апосеве и уборке урожая. аОбоснованы параметры рабочих органов; изучены схем вибропривода. аПроведены экспериментальные исследованияа работы подкапывающих и сепарирующих рабочих органов, по снижению потерь при уборке корнеплодов. В области внесения в почву удобрений и семян с использованием вибрационных технологий особо отмечены работы Н.М. Беспамятновой, посвященные вибрационным процессам при внесении в почву семян и удобрений, анализу колебаний и вибраций в технологических процессах. аЗначительный вклад в создание вибрационных аппаратов для подготовки удобрений, для внесения удобрений и семяна в почву, в методы частотного управления рабочими органами,а выбора параметров и режимов технологических процессов осуществлен в работах Н.М.Кулешова, В.А.Рычкова, А.С.Вишнякова, С.В.Кравченко, С.А.Овсянникова, В.Г.Захарченко,а Н.П.Боровинских, О.А.Пономаревой, Р.С.Рахимова.

Проанализированы аработы по применению вибраций в послеуборочных операциях. Большой вклад в изучение вибрационных технологий в послеуборочных операциях авнесли Н.Е. Авдеев, С.С. Алатырев, В.Н. Анискин, А.С. Архипов, А.М.Васильев, Н.Г. Гладков, В.В. Гортинский, В.П. Горячкин, А.Г. Громов, П.М. Заика, А.Н. Зюлин, А.И. Климок, И.Е. Кожуховский, Н.Ф. Конченко, Н.И. Косилов, В.А.Кубышев, П.Н. Лапшин, И.П.Лапшин, М.Н. Летошнев, А.А. Лопан, Е.А. Непомнящий, Г.Т. Павловский, Ю.В. Терентьев, Г.Д. Терсков, М.А. Тулькибаев, Н.Н. Ульрих,а И.Я Федоренко, В.М Фоминых, В.М.Цециновский, Р.Б.Яруллин. В их работах исследованы вопросы аповышения эффективности работы колеблющихся поверхностей, уменьшения энергоемкости процесса сепарирования. Развита теории вибрационного перемещения зерновых смесей,а моделирования реологических свойств сыпучих материалов,а поведения сыпучих материалов при вынужденных воздействиях, адвиженияа частиц в псевдоожиженных материалах. Рассмотрены устройства для разгрузки сыпучих материалов, транспортирования и смешивания сыпучих материалов. Исследовано влияние вибраций на технологические процессыаа в сыпучих материалах, на повышение эффективности работы вибрационных механизмов за счет использования дорезонансных, резонансных или зарезонансных арежимов работы.

Схематизированная структур этих областей на основании статистической обработкиа числа публикаций по соответствующему направлению представлена на рис.1.

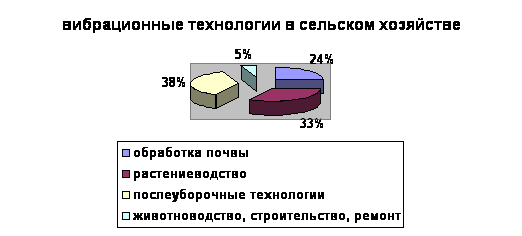
Рис.1 Структура областей применения вибраций.

Выделен класс сельхозмашин аВиЭМС с продольно-поперечными движениями рабочих органов. Определены направления повышения энергоэффективности и ресурсосбережения ВиЭМС рассматриваемого класса: почвообработка, растениеводство, послеуборочные технологии. Систематизированы вопросы моделирования, анализаа и диагностики электромеханических систем и составляющих их частей. Исследования, проведенные в рассматриваемых областях,а показывают, что: Ч в настоящее времяа в большинстве вибротехнологических сельскохозяйственных машин до сих пор используется электропривод с редуктором или с дебалансными механизмами;аа аа

Чзаявленные цели по энергоэффективности и ресурсосбережению влекут за собой детальный анализ обоснованности применения подобных кинематических схем электропривода;

Ч требует развития теория электромагнитных и энергетических процессов в ЭМ,а применяемых для привода РО вибрационных ТМ;

Ч отсутствуют исследования нелинейных колебанийаа рабочих органоваа ТМ,а представляющих собою пластины или оболочки, совершающиеа аколебанияа в сыпучей среде;

Ч недостаточно научное обоснование ВиЭМС как единого целого: источник энергии, двигатель, рабочий орган, рабочая среда, система управления;

Ч несовершенна научная база диагностики аВиЭМС по фактическому состоянию. а

Таким образом, аадля разработки новых аи модернизации существующих типов ВиЭМС требуются научно обоснованные методы моделирования и анализа как их составных частей, так и ТМ как единой системы из взаимодействующих между собой частей.

Для этого целесообразноа использовать математическое моделирование ЛАД, основанное на фундаментальных работах Вольдека А.И., Гольдберга О.Д., Беспалова В. Я.,а Иванова-Смоленского А.В., Копылова И.П., аЛитвина В.И., Львовича А.Ю., Малиновского А.Е., Мамедова Ф.А.,а Сарапулова Ф.Н., Скубова Д.Ю., Ходжаева К.Ш., аЯмамуры, аи топологический подход, присущий работам Г. Крона и Н.Хенкока.а Исследование ММ ЛАД и топологических свойств операторов ММ аЧ основныеа составляющие анализа электромагнитных и энергетических процессов в ВиЭМС. а

Для научного обоснования аразработки и модернизацииа рассматриваемого класса сельхозмашин, в работе выделены основные направления совершенствования методов моделирования и анализа :

Чсоздание аММ ВиЭМС на базе ЛАД, обладающих свойствами универсальности, системности, аналитичности, применимости в инженерной среде;

Чсовершенствование методов исследований ММ ВиЭМС и их составных частей;

Чразработка методов анализа операторов ММ.

Исследования, предпринятые в этих направлениях, асоздают научные основы разработки аи модернизации энергоэффективных сельскохозяйственных ВиЭМС путема совершенствования аММ ВиЭМС на базе ЛАД, методов моделирования рабочих органов ВиЭМС,а расчета аВиЭМС при совместной работе всех ее составных частей, теории преобразования энергии ва ВиЭМС.

В главе отмечен большой вклад в изучение задач о динамическом взаимодействии колебательных систем с источниками энергии ааклассических работ аВ.О. Кононенко, И.И.Блехманаа ,а К.В.Фролова , К.Ш.Ходжаева, А.Ю. Львовича, Д.Ю. Скубова.. Их исследования основываются ана использовании асимптотических методов, методов осреднения, малого параметра, разделении переменных для соответствующих операторных уравнений. Вместе с тем существует метод, позволяющий строить решенияа операторных уравнений ММ используя информацию об уравнении, заключенную в функции Грина.

Отражен вклад в развитие теории построения решений операторных уравнений с использованием функций точечного источника Г.Хермандера , В.С.Владимирова , Л. Шварца, В.Д.Купрадзе и М.А.Алексидзе, Г.Шмидта , В.В. Болотина, В.И. Астахова, аЮ.А.Бахвалова, С.Ю.Князева,а А.И.Маликова. Отмечено, что направление применения фундаментальных функций для построения решений уравнений в электромеханике атребует дальнейшего развития.

Проанализированы работы по повышению энергетических характеристик ЛАД и применению ЛАД в АПК. Отмечена вклад аА.И.Вольдека, О.Н. Веселовского, А.Ю. Коняева, Ф.Н. Сарапулова, Ф.А. Мамедова, А.Е Малиновского, В.И.Литвина, аБ.И. Петленко, Р.С. Аипова,а и др. Отмечено, что для расширения области применения ЛАД в АПК требуется развитие ММа ЛАД и методов иха исследования для использования устройств компенсации краевых эффектов и рекуперации энергии.

В главе показана необходимость эксплуатационной диагностики ВиЭМС и приведены сведения о методах диагностики электродвигателей и систем, которые разработаны в трудах ВИЭСХ,а Ю.С.Борисова,а О.Д.Гольдберга, С.В. Оськина,а А.И. Некрасова, С.О. Хомутова, аВ.С.Петухова, аи др.

На основании проведенного анализа сформулированы основные задачи диссертационной работы, выбраны методы аих решения, намечены направленияа экспериментальногоа исследования адекватности получаемых результатов, аразработкиа энергоэффективных аТМ для некоторыха направлений АПК и методов диагностики ВиЭМС.

Втораяа глава посвящена построению аналитических решений для векторного магнитного потенциала ЛАД на базеа применения функции Грина аи аметодам построения инженерных моделейа ЛАД, использующихся в приводе сельхозмашин. Исследования производились как для моделей с распределенными параметрами (уравнения в частных производных Ч УЧП), так и для математических моделей с сосредоточенными параметрами (обыкновенные дифференциальные уравнения ЦОДУ). Ва качестве базовой модели ЛАД принята известная модель конвективной диффузии са соответствующимиа начальными и граничными условиями. аИспользовано уравнение конвективной диффузии с переменными коэффициентами. Согласно этой модели векторный магнитный потенциал аЛАД, изображенного на расчетной схеме рисунка 2, может быть описан уравнениями в ао.е. авида:

,а (1) .

Краевые условия на бесконечностиа и начальное условие принимаются равными нулю. аВыше обозначено: а- векторный магнитный потенциал (ВМП), а- переменные пространства и времени, а- плотность тока обмотки индуктора, аа- скорость движения вторичного элемента (ВЭ), а- координаты концов ВЭ, а- функция амагнитной проницаемости индуктора,а -электрической проводимости, коэффициент . Остальные обозначения общеприняты.

Получение решения для векторного магнитного потенциалаа основывается наа аитерационной схеме

. (2)

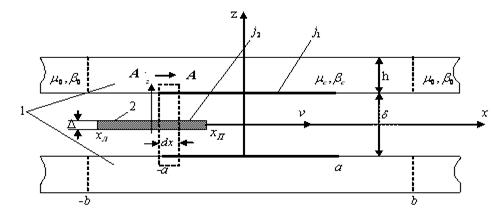
Рис.2 Расчетная схема одномерного ЛАД. 1 - индуктор, 2 - вторичный элемент.

В (2) используется свертка функции Грина левой части уравнения (1) с постоянными коэффициентами и правой части этого же уравнения. Схема основана на примененииа функции Грина соответствующего линейного оператора в совокупности с методом интегральных уравнений. При этом функция Грина вводитсяа для режима идеального холостого хода и адля режима нагрузки.

Приведены численно-аналитические решения задачи для различных случаев исполнения ЛАД. На рисунке 3 показаны кадры анимации вектор-потенциала аЛАД с коротким ВЭ. Темной полосой показано положение ВЭ.

Рис.3аа Графики потенциалаа в разные моменты времени.

Из рисунка 3 видно, что в месте прохождения ВЭ происходит провал волны ВМП. ВЭ движется с постоянной скоростью ав положительном направлении оси х, начиная от точек с координатами адо точек , пересекая в своем движении область первичной обмотки . В главе обоснована сходимость метода к точному решению задачи.

Для нужд практики разработана инженерная модель ЛАД, авключающая в себя три блока обыкновенных дифференциальныха уравнений.

Первый блок связан с описанием электромагнитного поля ЛАД.а Для описанияа поля использовано уравнение аконвективной диффузии типа а(1)

аа ,аа (3)

которое дополняется соответствующим граничными и начальным условиями

.а (4)

Здесьа а- электромагнитная добротность, а- координаты левой и правой границ ЛАД, , а- скорость подвижной части, а- начальное распределение векторного магнитного потенциала. Все выражения и величины в (3), (4) даны в о.е..

Приведенное УЧП заменяется двумя ОДУ первого порядка, полученными из него методом Бубнова - Галёркина. При этом арешение

и первичный ток

представляются в виде частичных сумм их разложенийа в ряды по собственным функциям задачи Штурма - Лиувилля, удовлетворяющим краевым условиям (4). Первый член ряда возбуждаемого электромагнитного поля выражается через анамагничивающие токи , а первый член соответствующего ряда для тока, выражается через первичные токи . Первый блок уравнений имеет вид:

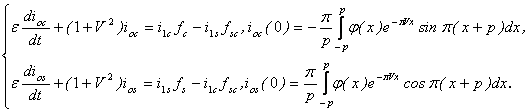а (5)

Второй блок уравнений связан с описанием электрических цепей индуктора.а Он задан двумя ОДУ первого порядка с соответствующими начальными условиями. Уравнения получены на основе баланса электрических сил в фазах индуктора и имеют вид:

(6)

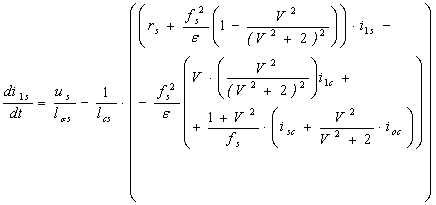Этим блоком определяются значения токов, потребляемых ЛАД из источника питания.

Третий аблок уравнений моделирует механическую цепь ВиЭМС. Описание механической цепи дано двумя ОДУ первого порядка с соответствующими начальными условиями. Уравнения получены наа основе балансов механических сил и перемещений. Этот блок определяет значенияа скорости аи перемещенияа аподвижной части амассой :

, аа а (7)

. (8)

Разработанная математическая модельа а(5)-(8) представляет собой нелинейную систему из шести ОДУ первого порядка с соответствующими начальными условиями. При необходимости, её можно расширить включением второго, третьего и так далее членов ряда ВМП. Каждый такой член добавляет в математическую модель два ОДУ. Адекватность модели подтверждается данными многочисленных публикаций, а также экспериментальными данными.

Для ВиЭМС с параметрами ЛАД: длинной -1м, шириной- 0,2м, зазором - 0,02м,а числом пар полюсов -2, апри максимальном числе проводников в пазу - 100, магнитной проницаемостьюа и электрическая проводимость вторичной части - соотвественно аГн/м иа 1/(Ом*м), массе подвижной части а2кг, пусковой силе и силе нагрузки -100Н и 50 Н, амплитуде фазного напряжения -393В и частоте а50 Гц было произведено моделирование по предложенной выше инженерной модели. На рисунках 4, 5а изображены результаты моделирования пуска ЛАД в режимеа холостого хода. Из рисунка 4 видно, что среднее значение электромагнитной силы стремится ка нулю, график скорости выходит на постоянную величину. Изображение рисунка 5 показывает, что потребляемая мощность стремится к константе, а полезная равна нулю.

Пусковые характеристики ЛАД при повышенной и пониженной добротностиа при наличии нагрузки изображены на рисунке 6. На нем изображены графики электромагнитной силы и скорости,а полученные при решении инженерной модели для добротностиа аи ао.е.. Значения пусковой силы и нагрузки принимались равнымиа 100 Н и 50 Н соответственно. аОстальные параметры брались, как и для случая ХХ ЛАД. аПредложенная инженерная модель применена к анализу различных типов ЛАД для ВиЭМС: при наличии накопителя энергии в виде пружины ( рисунок 7) и с разночастотным питанием( рисунок 8). Для рассматриваемых приводов получено, что КПД привода с пружиной составил 0,70,а в то время как КПД привода с разночастотным питаниема составил 0,67.а Поэтому при создании ТМ для АПК на базе ЛАДа предпочтительнее устройства с рекуперацией энергии,аа использующие пружины Таким образом, материал данной главы позволяют не только исследовать ВМП в ЛАД, но и проводить параметрическое моделирование дляа ВиЭМС, реализующих колебательные режимы работы РО при помощи ЛАД. Даны рекомендации для применения ЛАД в аАПК.

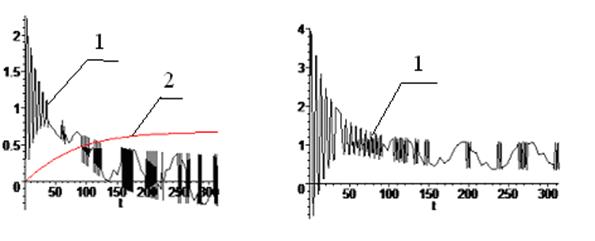
Рис. 4. Графики скорости -2 и электромагнитной силы -1

Рис.5. График потребляемой мощности -1

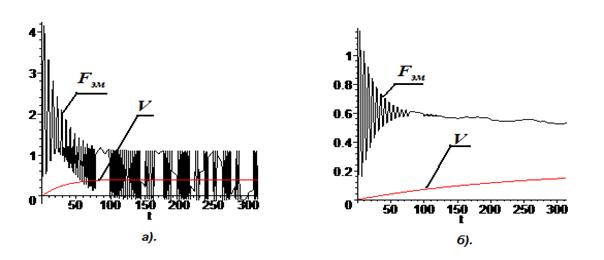
Рис.6 Графики электромагнитной силы и скорости

а).при добротности ,б). при .

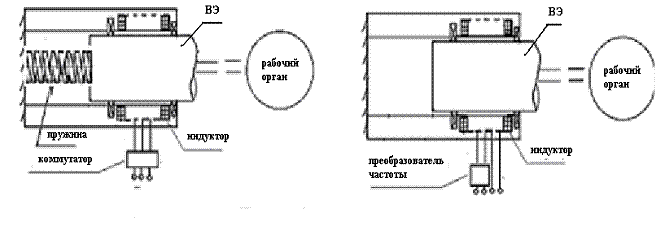
Рис.7 Принципиальная схема привода с трехфазным ЛАД и пружиной

Рис.8 Принципиальная схема привода с разночастотным питанием

аа Третья глава посвящена экспериментальному подтверждению адекватности аачисленно-аналитических решений, полученныха в главе 2. С этой целью был поставлен эксперимент по сравнению расчетных и экспериментальных данных для конкретного ЛАД. Эксперимент был проведен на кафедреа Электромеханические системы филиала МЭИ(ТУ) в г. Смоленске.а Эскиза ЛАД изображен на рисунке 9. Экспериментальная установка выполнена апо принципиальной схеме, априведенной на рисункеа 10.

Рис.9. Эскиз экспериментального ЛАД. 1- пакет индуктора, 2 - обмотка индуктора, 3 - вторичный элемент, 4 - измерительные катушки.

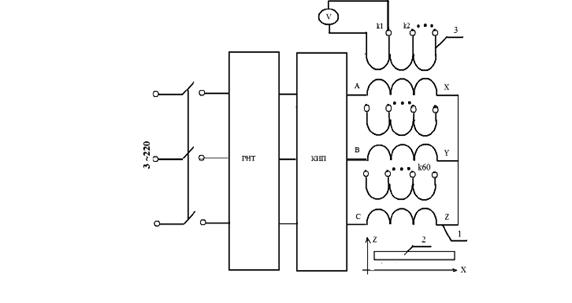
Рис. 10. Принципиальная схема установки. 1 -обмотка индуктора, 2 - вторичный элемент, 3 - измерительные катушки k1,Еk60.

Конструктивно установка являетсяа двусторонним ЛАД с шихтованным ферромагнитным ярмом для замыкания магнитного потока. Сердечники выполненыа шихтованными из листов электротехнической стали. Вторичной часть является алюминиевая шина. Эксперимент проведен для четырех случаев: режим идеального холостого хода (ИХХ)-рис.11, режим короткого замыкания (РКЗ) с положением ВЭ со смещением влево - рис.12, вправо относительно центра и по центру- рис.13, 14. Полученные экспериментальные данные на основе проведенной статистической обработки материалов свидетельствуют об адекватности решений, полученных при помощи разработанных моделей,а результатам эксперимента.

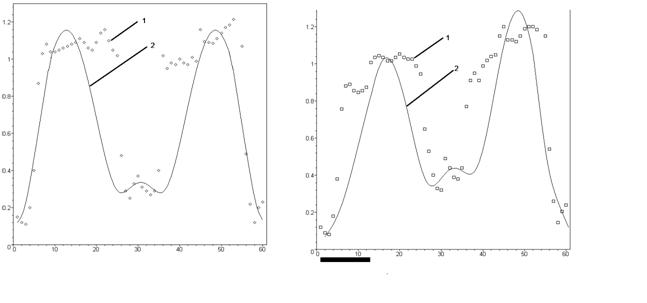
Рис. 11. Режим ИХХ ЛАД ааРис. 12. Короткий ВЭ.

1- экспериментальные данныеаа смещен влевоаа 2- результаты расчетаа аа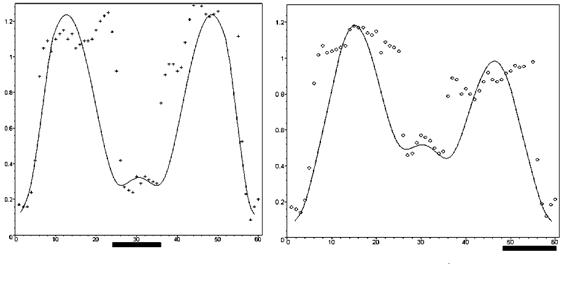

Рис.13.Короткий ВЭ размещен по центру Рис.14. Короткий ВЭ смещен вправо

Кроме этогоа экспериментально исследовано влияние длиныа ВЭ на распределение поля ЛАДа и получены данные, указывающие на необходимостьа учета геометрических параметров ВЭ при конструировании ЛАД с длинным индуктором. Экспериментально оценено влияние вида соединений обмотки в звезду или треугольник на поле в ЛАД. а

В четвертойа главеа приводятся результатыа расчетов аколебанийа ав асыпучей среде РО сельхозмашин, имеющих вид пластин или пологих оболочек. Считается, что среда находится в псевдоожиженном состоянии. Эти вопросы имеют важное значение при подборе режимов работы аТМ при вынужденных колебаниях, а также для создания рабочих органов удовлетворяющих задачам ресурсосбережения. Для научного обоснования исследований и получения практически применимых аналитических формул использован аасимптотический метод В.В.Болотина (АМБ). Задачи решались в нелинейной постановке. Применялись математические модели в форме записи Кармана дляа рабочих органов ТМ в виде прямоугольных в плане пластин и пологих оболочек.

Для исследования собственных колебаний прямоугольных в плане однородных тонких гибких прямоугольных пластина использованы уравнения Кармана

,а

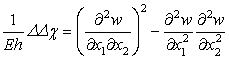Здесьа - функция прогиба, - функция усилий в срединной плоскости, -функция свойств среды, аD- цилиндрическая жесткость, h- атолщина пластины, E- модуль упругости, - плотность материала пластины,а - оператор Лапласа. Граничные условия для функцииа аформулировались стандартным образом, для функции усилийа - в среднем. В соответствии с основной идеей АМБ решение во внутренней области представлялось в виде

Здесь , , и ,а- неизвестные волновые числа и фазы, а- неизвестные постоянные, которые выбирались так, чтобы тангенциальные граничные условия удовлетворялись в среднем, а- неизвестная функция, если не идет речь о случае малых колебаний. Учитывая, что система уравнений Кармана следует аиз вариационного принципа Гамильтона-Остроградского

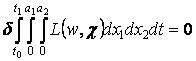
иа используя для построения приближенного решения осредненную по волновой ячейке плотность лагранжиана 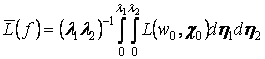, неизвестная функция аопределялась из вариационного уравнения 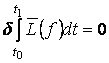. Уравнение Эйлера для этой вариационной задачи апри имеет вид

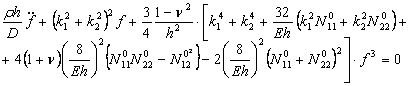.аа (9)

Решение уравнения а(9) искалось ав эллиптических функцияха Якоби в виде

, ,аа (10)

где k - модуль эллиптической функции, K(k) - полный эллиптический интеграл первого рода, ? - частота собственных нелинейных колебаний. При этом частота ? и модуль k эллиптической функции k удовлетворяют соотношениям:

а аа(11)

а а а(12).

Далее в главе приведены авыражения для ав зависимости от волновых чисел. С учетом динамического краевого эффекта получены уравнения для нахождения волновых чисел

Для различных видов краевых условийа найдены решения этой системы уравнений при помощи метода итераций. Сравнительный анализ с известными результатами для случая пластин в отсутствии сыпучей среды при аподтверждает адекватностьа результатов. На рисунке 15 приведены результаты для амплитудно-частотных зависимостей шарнирно-опертых и защемленных квадратных пластин.

Сравнительный анализ результов, приведенных на рис.15, ас известными результатами А.С. Вольмира, подтверждаета хорошееа соответствие дажеа для низших частот. Данные для пластин в сыпучей среде, полученные по этой же схеме, позволяют использовать их при создании новых рабочих органов ВиЭМС с учетом свойств сыпучей среды.

Рис.15 Амплитудно-частотные зависимости для нелинейных колебаний пластин

аа Аналогичным образом получены и результаты для собственных колебаний рабочих органов сельскохозяйственных ТМ, амоделями которых служат пологие тонкие оболочки. Для исследования колебаний в этом случае применяются ауравнения вида:

аа

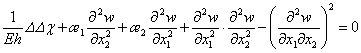. а аа

Граничные условия формулируются аналогично случаю пластин. Рассматриваются собственные колебания пологих оболочек.а Порождающее решение в области срединной поверхности, удаленной от кромок ищетсяа в виде

аа

а аа

Здесь n11, l11, n22,l22, n12, l12 - неизвестные параметры, независящие от координат и времени. Они выбираются из условия удовлетворения в среднем граничных условий в тангенциальном направлении. Кривизны обозначены через ,.а Используя вариационный принципа Гамильтона-Остроградского и идею осредненного по волновой ячейке лагранжиана, приходим ак нелинейному дифференциальному уравнению второго порядка относительно

. а аа

с начальными условиями , . Применив метод гармонической линеаризации, положим, что аи после преобразований получим

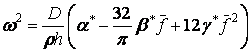, (13)

где обозначено

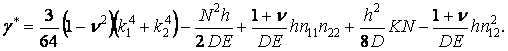
Введены следующие обозначения:

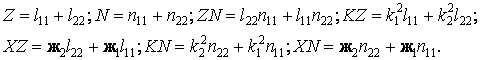
Неизвестные параметры ааи волновые числа анаходятся усреднением по контуру оболочки и решением уравнений стыковки соответственно. Результаты численного моделированияа зависимостиа амплитуды ота частоты ва о.е. для оболочек в отсутствии среды приведены на рисунке 16

Рис.16. Амплитудно-частотные зависимости для колебаний пологих оболочек.

На основании полученных результатов проведены исследования влияния тангенциальных граничных условий на частоты собственных колебаний, описан эффект группировки частот при больших прогибах около некоторой характерной частоты, обнаружено наличие точек бифуркации при пересечении скелетных кривых адля случая оболочек. Получено авлияние сыпучей среды на асдвиг резонансных частот в сторону более низких частот аколебаний. аРезультаты данной главы анеобходимы дляа использования на этапе проектирования новых РО ТМ сельскохозяйственного назначения дорезонансного, резонансного илиа зарезонансного типов.

В пятой аглаве изложено ааприменение метода функций Грина к нелинейным задачам моделирования ВиЭМС. Используются дифференциальные уравнения, описывающие электромеханическую систему в целом, а значит учитывающие взаимодействие электромагнитных и механических процессов в ВиЭМС.а Нелинейная постановка задачи апозволяет исследовать как различные законы питания ЭМ, так и воздействие на ВиЭМС законов управления. Вибрационная электромеханическая система аописывается с помощью системы дифференциальных уравнений первого порядка, записанной относительно характеристик электрической и механической частей системы следующим образом:

аа(14)

,а аа(15)

где аЦа вектор, координаты которого есть обобщенные координаты электромеханической системы (например,а фазные токи или потокосцепления, угловые скоростиа и т.п.); - вектор питающего напряжения статора или ротора, а также внешних моментов механической части системы; а - параметрическая матрица потокосцепления с постоянными элементами; Цвектор-функция, представляющая нелинейную связь, обусловленную произведением обобщенных координат или законом управления, - начальные условия. Такая постановка задачи позволяет моделировать ВиЭМС с различными типами апитания аи при наличии законов управления. Для получения решения системы (14) вводится аматрица Грина как решение системы дифференциальныха матричныха уравнений:

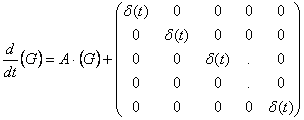Принято, что элементы матрицы Гринаа , а

представляют собою отклики электромеханической системы по обобщенной координате с индексом ана импульсное воздействие по цепи питания с индексом . С использованием интегральных преобразований и итерационной процедуры было найдено решение системы дифференциальных уравнений (14),а (15) по формулам

.а а(16)

В акачестве начального приближенияа принимается аотклик линейной части системы на заданное внешнее воздействие при нулевых начальных условияха .

Выражение (16) позволяет получать аналитические или численно-аналитические зависимости для характеристика рассматриваемых систем. Для ускорения сходимости итерационного процесса аучитываются изменения матрицы Грина на соответствующиха промежуткаха времени:

.аа (17)

Исследован аслучай ВиЭМС с низкоскоростным ЛАД. Ниже приведена принципиальная схема ВиЭМС и результаты математического моделирования. Сравнение результатов, полученных разными методами, показывает применимость предлагаемого метода к амоделированию ВиЭМС.

Кинематическая схема электроприводаа колебательного движения

1-демпфирующий элемент, 2- вторичный элемент, 3 - пружина, 4 - индуктор, 5 - блок управления ЛАД.

Изменение во времени скоростиа ВЭ

-Расчет методом Рунге-Кутта

7-а Расчет методом функций Грина

Рис.17. Кинематическая схемаа и графики изменения скорости

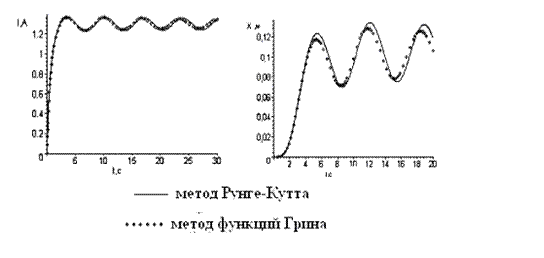
.Рис.18. Ток индуктора, рассчитанный разными методами

Рис.19. Перемещение ВЭ, подсчитанное этими же методами

аа В этой же главе производится анаучное обоснование аметода диагностикиа аВиЭМС, построенного на основном свойстве матриц Грина - информации о состоянии и характеристиках системы. Эта информация может быть получена для любой системы путем воздействия на нее импульсными источниками заданной мощности.а Показано, что если воздействие осуществляется точечными источниками, тоа отклики системы формируют матрицу Грина. Если воздействие осуществляется функцией Хевисайда, то отклики системы формируют интегральную матрицу Грина. Получаемые матрицы откликов являются функциональными матрицами, но, тем не менее, аони путем обработки их элементов преобразуются в числовые матрицы. Это оказывается удобным для хранения и сравнения этих матриц с эталонными для исследуемого объекта матрицами. Путем сравнения числовых матриц текущего состояния системы с эталонной матрицей этой же системы делаются заключения о текущем состоянии системыа и о месте возникновения дефектов. Разработана методика оценки текущего состояния электрических двигателей с фазным ротором, защищенная патентом [52]. По этой методике в соответствии с принципиальной схемой (рис.20) проводились измеренияа ва фазаха двигателя по определенной циклической схеме.

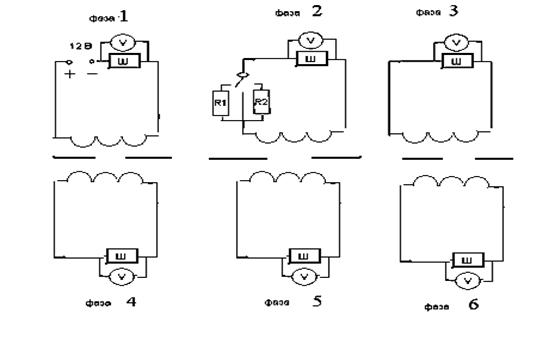
Рис.20 Принципиальная схема опыта по диагностике ЭД с фазным ротором.

Опыты осуществлялись как для двигателя со всеми исправными фазами, так и для случая неисправностей в обмотке одной из фаз.а На фазу 1 статора эталонного асинхронного двигателяа с активным сопротивлением 3 Ома подавалось постоянное напряжение амплитудой 12 Ваа в виде функции Хевисайда. За это же самое время с обмоток а1, 2, 3, 4, 5, 6 (Рис.а 20 ) одновременно снимались показания цифровым запоминающим осциллографом PCS500, при одинаковых сопротивлениях ашунтов (Ш) 0,25 Ом. Опыт циклически повторялся для каждой фазы двигателя. Имитацияа повреждения обмотки проводилась включением дополнительного сопротивления в цепь фазы 2 статораа (Рис. 20 ). Экспериментальные данные в обмотках без повреждений и в обмотках с повреждениями приведены на рис.21,22. На рисунке 21 представлена осциллограммаа для обмоток с неповрежденными фазами. На рисункеа а22 представлена осциллограмма для обмоток при наличии повреждения, которое моделируется сопротивлением 10 Ом. аДанные осциллограмма используются для построения матрицы Грина.а Информации, содержащаяся в матрице Грина и представленная таблицей 1, апо аналогии с реляционными базами данных хранится виде массивов (таблиц).

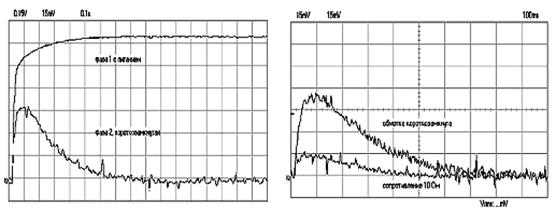
Рис.21. Обмотки с неповрежденными фазами.

Рис.22. Обмотка при наличии повреждения

Таблица 1. Элементы интегральной матрицы Грина.

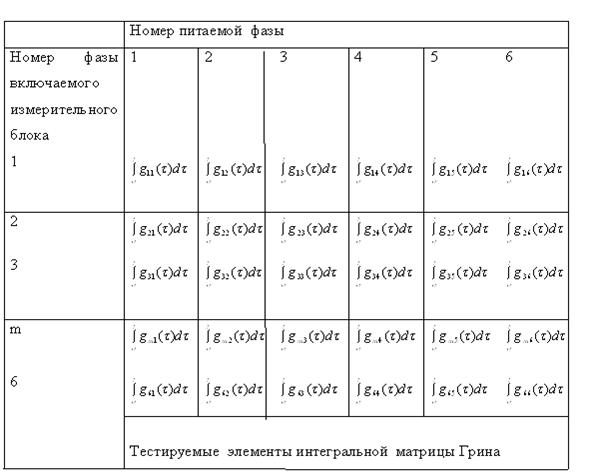
Предложен критерий оценки текущего состояния адвигателя на основе сравнения аэлементов матрицы Грина этого состояния с соответствующими элементами эталонной матрицы Грина.а Обосновано применение микропроцессорной техники для использования этого критерия. Рассмотрены случаи применения вышеописанного алгоритма для систем, авыведенных из рабочего состояния.

Шестая глава посвящена развитию теории энергетическиха процессов в ВиЭМС. ВиЭМС на базе ЛАД является несимметричной электромеханической системой. Теоретические основы преобразования энергии в таких системах в настоящее время разработаны слабо. Основным элементом аразработанной теории являетсяа матричнаяа ММа электромагнитных и энергетических процессов в ЭМ. Информация о механической части ВиЭМС вводится в ММ с помощью задания угловой (линейной) координаты ротора (или ВЭ) .а ВиЭМС представлена алинейным оператором с матрицей , который в векторном пространстве токова осуществляета преобразование координата . Базисы, в которых записаны векторыа статора и ротора , связаны углом .а В модель входят и соотношения, определяющие эффективность электромеханического преобразования энергии:

мощность электрических и магнитных цепей аВиЭМС

();

мощность механического входа ВиЭМСаа

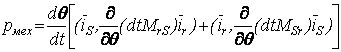Для исследованияа энергоэффективности введеноа понятиеа совокупной мощности линейного оператора . Это выражение фактически является моделью мощности ВиЭМС.

Кроме того, дляа исследования топологическиха свойств апредложено использовать данную аматематическую модель в виде .аа В соответствии с записанной формулой, очевидно,аа чтоа при фиксированном внешнем воздействии ав ЭМ возможны только токи, определяемые условиями существования матрицы . Определен комплекс топологических свойств ВиЭМС Ч свойства параметрической матрицы , векторного пространства аи поля мощности ЭМ. Развита концепция по использованию топологических свойства ММ ВиЭМС адля анализа происходящих в них процессов.а Разработанная модель ориентирована на матричные исследования энергетическиха процессов аи многопараметрическую (матричную) диагностику ВиЭМС.

В качестве еще одного элемента теории энергетических процессов разработаны вопросы приводимости матрицы оператора ЭМ в пространства меньшей размерности с учетом ограниченийа на векторы напряжений и токов, накладываемые схемой соединений обмоток. Особое внимание уделено матрицам взаимной индукции ротора и статораа ()а и (). Для исследования вопросов приводимости использованаа векторно-матричная модель ЭМа вида:

Векторы азаданы в системе координата ротора, а векторы в системе координата статора; а- матрица индуктивных сопротивлений взаимной индукции ротор-статор; а- аналогичная матрица статор-ротор, а- скольжение. Матрицы аявляются собственными параметрическими матрицами статора и ротора, включающими в себя диагональные матрицы параметров рассеяния аи квадратные матрицы самоиндукции статора и ротора . Наличие в составе аматриц рассеяния гарантируета существование обратных матриц . Это позволило исключением вектора тока ротораа записать уравнение машины в трехмерном пространстве токов статора:

,аа (18)

где

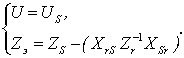
Этот подход позволил исследовать параметрические свойства ЭМ, выявить область существования решений задачи приводимости ЭМ.аа Показано, что не все токи ротора способны трансформироваться в токи статора. Такая ситуация может возникать при диагностировании обмоток ротора, когда диагностическими факторами служат токи статора. Полученное решение является одним из элементов научного обоснования способов диагностики ЭМ. Кроме этого, показано, что обязательным элементом электромеханического преобразования энергии являетсяа наличие преобразования векторов тока статора и ротора в плоскость ненулевых собственных векторов матриц взаимной индукции.

В главе также осуществлен анализ квадратичных форм аэлектромагнитной мощности обмотки статора и квадратичной формы механической мощности. На основе понятия квадратичной формыа создана авизуальная модельа потоков мощности для симметричных и несимметричных ЭМ.а При соответствующем выборе системы координат квадратичная форма мощности преобразуется к каноническому виду:

, (19)

гдеа адиагональная матрица,а состоящая из собственных чисел матрицы ЭМ. Это позволяет анализировать состояние мощности ЭМ в зависимости ота схемы соединения и вида питания.а При фиксированной мощности,а выражение (19) представляет собой уравнение поверхности в пространстве размерности m. Разработанные модели ориентированы на визуальное решение задач минимизации мощности рассеяния. Развита концепция визуализации мощности ЭМ при помощиа изображения поверхностей неизменнойа мощности (поверхностей уровня). Приведеныа примерыа поверхностей неизменной мощности трехфазных обмоток. Поверхности строились по выражению (19). С помощью поверхности показано, что одна и та же мощность может быть реализована различными системами фазных токов. В связи с этим выделено геометрическое место малых токов (ГММТ). аКонтур ГММТ, обозначенный на рисунке 23 символом , строился по выражению (19) при условии, что . На графиках показаны главные оси, связанные с базисом , аи оси фаз обмоткиа . Положение вектора минимального тока соответствует точке пересечения ГМТ с осьюа .

Дляа несимметричной трехфазной обмоткиа с собственными числаа матрицы этой обмотки равными соответственно , поверхность неизменной мощности обмотки задается уравнением. Это уравнение представляет собой эллипсоид изображенный на рис. 23. Любой точке поверхности соответствует определенный модуль вектора тока, равный . Величины модулей тока для аточек поверхности неизменной мощности находятся между минимальным значением на оси а(о.е.) и максимальным значением на оси а(о.е.). Таким образом, при неизменной мощности модуль тока данной обмотки может изменяться в араз. Компонента вектора тока асвязана, в основном, с мощностью рассеяния, так как она удаляет вектор тока от ГММТ. Для точек, лежащих вне осей ГММТ, эти токи представляют собой несимметричные трехфазные системы, а для точек на осях - однофазные системы токов..

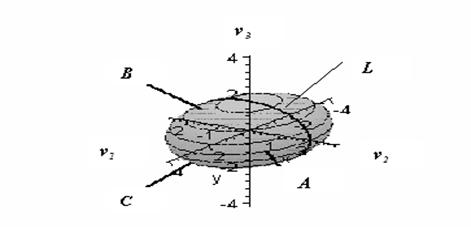
Рис.23. Поверхность неизменной мощностиа несимметричной обмотки

аа В главе проанализирована также анесимметричная обмотка с вырожденной параметрической матрицей. В трехфазном исполнении матрицы параметров обмотки имеют одно собственное число, равное нулю. У таких обмоток (к ним, в частности, относятся и симметричные обмотки) токи, отвечающие нулевому собственному числу,а являются особыми. Поверхность неизменнойа мощности представляет собой эллиптический цилиндр, ориентированный по осиа отвечающей нулевому собственному числу. Особые токи ав подобных обмотках участвуют только в рассеянии энергии. Их исключение из состава фазных токов в любом случае рационально и осуществляется питанием обмотки токами, принадлежащими ГММТ.

Для оценки энергетической эффективностиа процессов преобразованияа аэнергии в ЭМ использована концепция аи подмножеств токов. Токи этих подмножеств выбираются из условий:

Векторы продольного () и поперечного аподмножеств в канонических базисах строились для той же обмотки, визуальная модельа которой приведенаа выше. На приведенных ниже рисункаха 24, 25 подмножества токова показаны полем стрелок. Отмечается, что векторы продольного подмножества ортогональны поверхности неизменной мощности . Векторы поперечного подмножества принадлежат касательным к этой поверхности плоскостям. Для наглядности поверхность неизменной мощности тоже приведена на рисунках 24, 25. Для несимметричной обмотки с параметрической матрицей общего вида векторы апродольного подмножества показаны на рисунке 24. Канонические оси аобозначены наа рисунке асоответственно. Плотность векторов подмножества тем выше, чем выше значение эффективного собственного числа ав данном направлении.

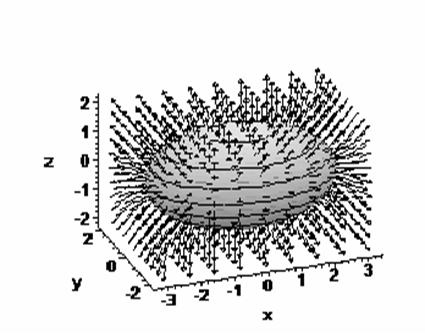
Рис.24. Поле векторов продольного подмножества токов несимметричной обмотки

Векторы поперечного подмножестваа токова обмотки показаны на рисунке 25. Ориентация векторов апо всем направлениям векторного пространства свидетельствует о том, что эффективное собственное число аизменяется при любой вариации координат. Плотность векторов подмножества тем ниже, чем ниже значение эффективного собственного числа в данном направлении.

Рис.25 Поле векторов поперечного подмножества токов несимметричной обмотки

Проанализирована также несимметричная обмотка с вырожденной параметрической матрицей. Вырожденность параметрической матрицы по оси а(ось ) приводит к тому, что векторы продольного подмножества имеют нулевые координаты по этой оси. Относительно других осей можно отметить, что поток мощности (плотность векторов ) более интенсивен по осиа(ось ) и менее интенсивен по оси а(ось ). Это связано с различием собственных чисел матрицыа апо этим осям.а С токами, принадлежащими асвязаны энергетические обмены и избыточные потери энергии.

Понятие о d- и q- подмножествах токов позволяет формировать рациональное питание ВиЭМСа вектором питающего напряжения по критерию минимума

Отмечено, что рациональное питание объекта осуществимо путем реализации его мощности за счет токов подмножества анастолько, насколько это физически возможно, технически и экономически целесообразно.

На визуальных моделях были оценены возможности реализации этого принципа для электротехнического оборудования. Расчеты, проведенные на основе визуальных моделей для серийного асинхронного двигателя 4А160S4У3 мощность 15КВт , позволили оценить результаты нарушения параметрической однородности фаз. Результаты относятся к случаю повышения сопротивления рассеяния одной из фаз на 10% вследствие эксплуатационного старения или механического (электрического) повреждения. Они свидетельствуют о том, что изменение сопротивления одной из фаз на 10% приводит:

- к увеличению апотребления активной мощности на 3,5%;

-а к увеличению реактивной мощности наа 3,3а %;

- к появлению поперечного энергообмена мощностьюа 92,6 ВА, отсутствовавшегоа у двигателя без повреждений.

аа Положения, выводы и результаты этой главы являются базой адля научного обоснования и ареализации энергосбережения в таких областях практической электротехники,а гдеа имеет место существенная параметрическая неоднородность объекта или группы объектов. Это особенно касается электрооборудования осветительных электрических сетей, производств с неполнофазным, однофазным и групповым включением электрооборудования в сельском хозяйстве.

Седьмая глава посвящена разработке энергоэффективных вибрационных электромеханических систем сельскохозяйственного назначенияа с продольно-поперечными движениями рабочих органов. В частности рассмотрены аВиЭМС применяемые для операций посева, сушки и сортировки продукции и приготовления смесей.а При разработке этих систем использована основная идея работ Ф.А.Мамедова и его школы, асостоящая в удалении из системы привода энергопоглощающих подсистем. аа Наиболее приемлема эта идея для систем с продольно-поперечными движениями рабочих органов, так как она позволяет упростить кинематическую схему ТМ,а устранив лишние передаточные звенья ( редукторы, карданные передачи и др. механизмы).а Это осуществимо путем применения ЛАД с рекуперацией энергии при помощи пружины (механической или электрической). При использовании кинематических схем ТМ с ЛАД решается не только задача энергоэффективности, но и задача ресурсосбережения (за счет упрощения кинематической схемы или применения менее материалоемких РО).а Рассматриваемый в главе подход позволяет решать азадачи разработки новой и модернизации существующей техники, так как конструкция ТМ в целом остается неизменной, а меняется лишь часть, отвечающая за преобразование электрической энергии в механическую. К тому же этот подход очень хорошо согласуется с направлением применения в сельском хозяйстве энергонасыщеных тракторов, так как позволяет применять разработанные ВиЭМС путем непосредственного подключения в электрическую сеть трактора без дополнительных механических передаточных устройств. Он создает определенные преимущества, особенно для передвижных технологических машин. Приведены разработки авысевающего аппарата сеялки, защищенныеаа патентами [47,59]. Конструкция амодернизированного высевающего аппарата приведена ниже на рисунке 26.

Рис. 26а Высевающий аппарат сеялки

Экономический эффект модернизации для рассмотренного случая заключается в ресурсосбережении, повышении энергоэффективности и улучшении технических характеристик конструкции.а В АПК РФ ав 2010 году, в соответствии со статисическими данными, априменялось около 100000 сеялок. В результатеа их модернизации будет сохранено минимум а1000 тонн металла и а50000 квт аэнергии. Суммарный экономический эффект от модернизации может составить как минимум 20 млн.рублей ва рамках АПК. К тому же у модернизированной конструкции лучше технические характеристики за счет управляемости процессом работы в зависимости от характеристик посевного материала. Экономический эффект в этом случае определяется экспериментальным путем, но по оценкам некоторых авторов он может достигать адо 1000 рублей в год на одну сеялку.

Для задач сушки сельскохозяйственной продукции с различными характеристиками сыпучей среды разработаны конструкции вибрационных сушилок и сушильных комплексов, защищенныеаа патентами [ 49,55-59] и ачастично представленные на рисункаха 27,28.

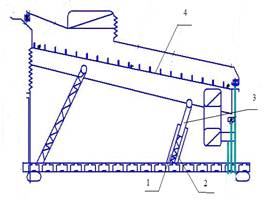
Рис. 27а Односекционная вибрационная сушилка. 1-ЛАД, 2-пружина, 3-ВЭ, 4- вибрационная решетка.

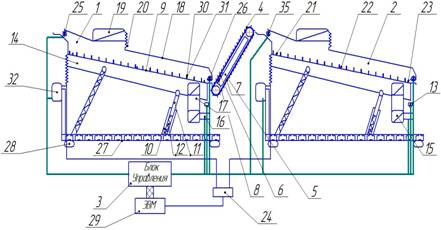
Рис. 28 Многосекционная вибрационная сушилка. Патент [55]

аа Для задач приготовления смесей (подготовка удобрений, обработка посевного материала, кормопроизводство и др.) разработаны вибрационные смесители с электромеханическими вибраторами, защищенные патентами [ 51-54] и приведенные на арисунке 29.

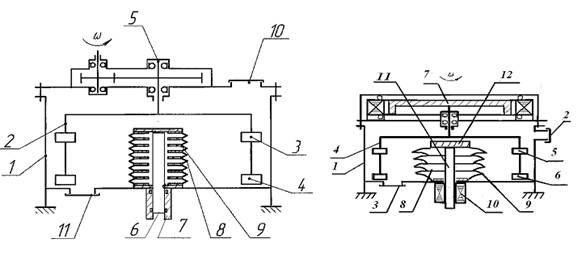
Рис. 29а Вибрационные смесители.

Экономический эффект от применения разработанного ряда сушилок и смесителей составляет не менее 2000 рублей в года на один агрегат при снижении энергоемкости на 15%, материалоемкости ана 10%.

аОсновные результаты и выводы.

В диссертационной работе на основе теоретических и экспериментальных исследованийа решенаа важнаяа научно-техническая проблемаа увеличения энергоэффективности и снижения материалоемкости авибрационного технологического оборудования АПК РФ. Разработаны новые инженерные модели ВиЭМС, получены аналитические амплитудно-частотные зависимости для арабочих органов ТМ с учетом взаимодействия с сыпучей средой, усовершенствованы аметоды арешения нелинейных задач,а модернизированы аВиЭМС адля посева, сушки и смешивания.

При решении поставленных азадач получены следующие арезультаты:

Разработана универсальная инженерная математическаяа модель ВиЭМС на базе ЛАД и развита итерационная математическая модель ЛАД. Она необходима адля расчетов различных вариантов конструкций и электромагнитных нагрузок при создании энергоэффективных, ааресурсосберегающих ВиЭМС. Экспериментально подтверждена адекватность разработанных математических моделей;
Проведен сравнительный анализ ЛАД с рекуперацией энергии посредством пружины по отношении к ЛАД с разночастотным питанием на основе разработанных инженерных моделей. Получены результаты, показывающие преимущества аВиЭМС на базе ЛАД с рекуперацией энергии,а применимые при создании ТМа для АПК.
Развиты методы расчета колебаний рабочих органов ТМ при апоперечных перемещениях в сыпучей среде. Получены амплитудно-частотные зависимости для поперечных колебаний рабочих органов ТМ в виде тонких пластин и пологих оболочек с учетом взаимодействия со средойа в случае больших отклонений от положения равновесия. Отмечены эффекты группировки частот и влияние параметров среды. Результаты необходимы при разработке ресурсосберегающих РО для ВиЭМС дорезонансного, резонансного и зарезонансного типов;
Разработана численно-аналитическая математическая модель для исследования нелинейных ВиЭМС. Модель позволяет отыскивать аналитические приближенияа и производить параметрическое исследование ВиЭМС при произвольном режиме питания и с учетом закона управления. Модель предназначена для осуществления предварительных ааналитических расчетов динамических режимов ВиЭМС ;
Разработаны научные основы многопараметрической диагности ВиЭМС. Предложен, защищенный патентом,а метод диагностики электромеханических систем на основе матриц Грина. Метод позволяет путем сравнения текущего аи эталонного состояний ЭМС определять место и степень дефекта в ВиЭМС, а такжеа может служить основой для построения микропроцессорных систем диагностики ВиЭМС;
Впервые предложены методы визуализации энергетических процессов в ЭМ и введены понятия подмножеств токов ЭМ, позволившие проанализировать особенности электромагнитных и энергетических процессов ва электрооборудовании сельского хозяйства;
Разработаны, научно обоснованы и защищены патентами энергоэффективные и ресурсосберегающие аВиЭМСа для посева, сушки сельхозпродукции и приготовления смесей;
Осуществлено внедрение результатов работы: в концерне Русэлпром при созданииа серии двигателей 7AVE и энергонасыщенных тракторов Беларус-3023, ав ОАО Амкодор республики Беларусь при модернизации зерноочистительно-сушильных комплексов ЗСК-40Ш, ав учебный процесса филиала ФГБОУ ВПО Национальныйа исследовательский университет МЭИ в г. Смоленске.

Содержание диссертации опубликовано в следующих работах:

Работы в журналах из перечня ВАК:

Денисов В.Н. Продольно-поперечные колебания неоднородного стержня переменного сечения при наличии опорного устройства//аа Труды МФТИ,серия УАэрофизика и прикладная математикаФ,1975,ч. 1
Курилин С.П., Денисов В.Н. Одномерный расчет переходного электромагнитного процесса в ЛАД методом Бубнова-Галеркина.// Электротехника. - 1981. - № 11. - С. 54 - 56.
Жинжер Н.И.,Денисов В.Н.а Асимптотическийа метода в задаче о нелинейных колебаниях оболочек//Проблемы прочности, № 9,1983
Жинжер Н.И., Денисов В.Н.а Асимптотический метод в задаче о нелинейных колебаниях изотропных прямоугольных пластин// Изв.АН СССР, мех.тв. тела, 1985, №1. С.152-158.
Денисов В.Н., Ершова Л.Н..,Кислицын В.И.,Козлов А.Е. Создание автоматизированного банкаа данных для прогнозирования техничес. сост. и планир. ремонтов основного оборудования.//Энергетика, 1985,№7. С.22-23.
Мамедов Ф.А., Денисов В.Н., Курилин С.П., Хуторов Д.В. Варианты построения математической модели линейной машины.// Электричество. - 2000. - №10. - С. 35 - 39
Мамедов Ф.А., Денисов В.Н., Курилин С.П. Особенности энергетических процессов в электрических машинах с асимметричными обмотками.// Электричество. - 2002. - №9. - С. 36 - 43.
Денисов В.Н., Курилин С.П. Преобразование координат и анализ параметрических свойств электрических машин// Электричество,а №6, 2007.- С. 45-50.
Мамедов Ф.А., Денисов В.Н., Курилин С.П. Применение функций Грина к анализуаа электрооборудованияа в сельском хозяйств// Техника в сельском хозяйстве, 2008, 2.
Денисов В.Н. Метод функций Грин и моделированиеаа электромеханическиха система с линейнымиа двигателямиаа дляа АПК// Механизация и электрификация сельского хозяйства, 2008,а 6.
Денисов В.Н. Линейныеаа асинхронные двигателиа в энергосберегающих технологиях АПК// Наука и технологии. Том 2. Труды XXVIII Российской школы.- М.: РАН, 2008.- с. 306 (С.193-201).
аМамедов Ф.А., Денисов В.Н., Хромов Е.В. Линейный электропривод для вибрационного смесителя сыпучих кормов// Тракторы и сельхозмашины.-2010.- 6.- С.20-22.
Денисов В.Н., Курилин С.П. Микропроцессорная диагностика электромеханических систем // МЭСХ, № 9, 2010.-а С.17-18.
Денисов В.Н., Курилин С.П. Инженерная модель линейного асинхронного двигателя// Электричество, 2011, №3. - С.52-54.

Монографии и пособия с грифом УМО:

Курилин С.П., Денисов В.Н., Круглов В.В. Матричная теория электрических машин.аа Печаа М.: АНО ВПО ЦС РФ Российский университет кооперации , 2008.-128 с.: ил. ISBN 978-5-94771-102.
Денисов В.Н., Курилин С.П. Матричное моделирование электромагнитных и энергетических процессов в электрических машинах.:учебное пособие/ В.Н.Денисов, С.П.Курилин, под.ред Денисова В.Н.-Смоленск:РИО филиала ГОУВПО МЭИ(ТУ) в г.Смоленске, 2011.-140 с..

Работы в трудах конференций и журналах:

Денисов В.Н. Применение асимптотического метода для анализа собственных нелинейных колебаний упругих пластин// Труды МЭИ, вып.578,1982.С.79-80.
Денисов В.Н.а Применение асимптотического методаа ка исследованию собственных колебаний цилиндрических оболочек при больших прогибах//В кн.:а Актуальные проблемы механики оболочек. Тезисы докладов Всесоюзной школы, Казань,КАИ,1983.
Мамедов Ф.А., Денисов В.Н., Курилин С.П., Хуторов Д.В. Исследование электромагнитных процессов в линейном электродвигателе с коротким вторичным элементом.//IV Межд. конф. Электротехника, электромеханика и электротехнологии МКЭЭЭ: Сб. тр. - 2000. - М., 2000. - С. 326-327.
Мамедов Ф.А., Курилин С.П., Денисов В.Н., Хуторов Д.В. Асимметричные электромеханические преобразователи энергии вращательного и поступательного движения для АПК. // РГАЗУ - агропромышленному комплексу./ Сб. научн. тр. в 2-х ч. - ч.2 - М., 2000. - С.238 - 241.
Мамедов Ф.А., Денисов В.Н., Курилин С.П. Параметрические свойства и особенности энергетики асимметричных обмоток электрических машин.// IV Межд. симпозиум ЭЛМАШ - 2002: Сб. тр. - 2002. - М., 2002. - С. 85 - 88.
Курилин С.П., Денисов В.Н. Энергетические показатели электрических машин при полигармонических и апериодических функциях фазных токов.// 5-ая Межд. конф. МКЭЭЭ - 2003: Сб. тр. - 2003. - Ч.1 - Крым, Алушта, 2003. - С. 563 - 566.
Денисов В.Н., Курилин С.П. Визуальные модели мощности многофазных обмоток.// Перспективы и тенденции развития электротехнического оборудования./ V Межд. симпозиум ЭЛМАШ - 2004 11 - 15 октября 2004 г.: Сб. тр. - М., 2004. - С. 105 - 111.
аДенисов В.Н., Курилин С.П. Визуализация математических моделей мощности многофазных обмоток.//Материалы международной научно-технической конференции Электромеханические преобразователи энергии. Россия, Томск, 20 Ц22 октября 2005 г. - С. 131-134.
Денисов В.Н., Курилин С.П. Параметрическая матрица электрической машины переменного тока.//а Актуальные проблемы энергосберегающих электротехнологий. Труды Всероссийской научно-технической конференции с международным участием. Екатеринбург: ГОУВПО УГТУ - УПИ, 2006 - С.200 - 202.а
Денисов В.Н., Курилин С.П.Преобразование координат и параметрические свойства электрических машин переменного тока.// Актуальные проблемы энергосберегающих электротехнологий. Труды Всероссийской научно-технической конференции с международным участием. Екатеринбург: ГОУВПО УГТУ - УПИ, 2006 - С.203 - 207.
Денисов В.Н., Курилин С.П. Использование векторных пространств в математическом моделировании электрических машин.// Информационные технологии в электротехнике и электроэнергетике. Материалы VI Всероссийской научно-технической конференции. Чебоксары. 7-9 июня 2006 г.- Изд-во ЧГУ, Чебоксары, 2006.-С.110-113.
Денисов В.Н.О сходимости одного итерационного метода теории ЛАД// XI-я Межд. конф. Электромеханика, электротехнологии, электротехнические материалы и компоненты. Труды. Часть 2.аа Ца 18-23 сентября 2006 г. Крым, Алушта. - С. 283 - 284.аа
аа Денисов В.Н., Курилин С.П. Особенности параметрических матриц электрических машин//а XI-я Межд. конф. Электромеханика, электротехнологии, электротехнические материалы и компоненты. Труды. Часть 1.аа Ца 18-23 сентября 2006 г. Крым, Алушта. - С. 260 - 261.аа
Денисов В.Н., Курилин С.П. Виды и свойства параметрических матриц математических моделей электрических машин// Информационные системы и модели в научных исследованиях, промышленности и экологии. Доклады V всероссийской научно-технической конференции.- Тула: Изд-во ТуГу,2006.-С. 115-117.
Денисов В.Н. Оба итерационном методе решения краевой задачи для дифференциальных уравнений второго порядка.// ПРИОРИТЕТНЫЕ НАПРАВЛЕНИЯ РАЗВИТИЯ НАУКИ И ТЕХНОЛОГИЙ.. Книга II. Всероссийская научно-техническая конференция в 2 кн./Под общей редакцией чл.корр.РАНа В.П. Мешалкина .-М.;Тула: Изд-во ТуГУ,2006.-С.121-123.
Денисов В.Н., Курилин С.П. Подход к вопросам энерго- и ресурсосбережения в АПК с использованием свойств матриц//а Вестник РГАЗУ. Научный журнал №1(6). Москва, 2006.- С.242-243.
Денисов В.Н., Курилин С.П. Преобразования координат в системном подходе к вопросам энерго- и ресурсосбережения в АПК// Вестник РГАЗУ. Научный журнал №1(6). Москва, 2006.- С.243-245.
Денисов В.Н. Применение дискретных методов в математическом моделировании электрических машин//аа Динамика нелинейных дискретных электротехнических и электронных систем. Материалы VII Всерос.научн.-техн.конф. Чебоксары: Изд-во Чуваш. Ун-та, 2007.- 338с.(С.328-331).
Денисов В.Н. Применение мехатронных технологий в моделированииа сельскохозяйственныха виброустановок.// Вестник РГАЗУ. Научный журнала а№ 3 (8а ). Москва, 2007.- С.164-166.
Мамедов Ф.А., Денисов В.Н., Курилин С.П. Применение функций Грина к анализуа электромеханических систем при диагностике и проектировании электрооборудования в сельском хозяйстве// Энергообеспечение и энергосбережение в сельском хозяйстве. Труды 6-й Межд.научн.-техн. конференции ( 13-14 мая 2008 гд, г. Москва, ГНУ ВИЭСХ). в 5-ти частях. Часть 3. Энергосберегающие технологии в животноводстве и стационарной энергетике.
Денисов В.Н. О применении функций точечного источника в математическом моделированииа процессов в электромеханических системах// Математические методы в технике и технологиях.- ММТТ-21.[текст]: сб. трудова ХХI Международ. науч. конф.: в 10 т.Т.5 Секция 11/ под общ.ред. В.С.Балакирева. Саратов: Сарат.гос. ун-т, 2008.-С.203-205.
Денисов В.Н.Линейныеаа асинхронные двигателиа в энергосберегающих технологиях АПК Докл.аа Наука и технологии. Секция 5. Новые технологии.-Краткие сообщения XXVII Российской школы. Екатеринбург: УрО РАН. 2008.-116 с.(С.79-82).
Денисов В.Н., Курилин С.П. Метод расчета нелинейных электромеханических системаа Докл.аа XII-я Международная конференция. Электромеханика, электротехнологии, электротехнические материалы и компоненты. Труды.-29сентября-4 октября, Крым, Алушта, 2008.- С.201.
Денисов В.Н., Курилин С.П. Основы матричной диагностики асинхронных электродвигателей Докл.аа Математические методы в технике и технологиях - ММТТ-22[текст]:сб.трудов XXII Междунар.научн.конф.: в 10 т. Т.8 Секция 9/ под общ.ред. В.С. Балакирева.-Псков: Изд-во Псков. гос. политехн. ин-та, 2009.-244 с.(С.71-74) ISBN 978-5-91116-101-3(T.8)ISBN 978-5-91116-087-2.
Денисов В.Н. Совершенствование методов анализа и диагностики электромеханических системаа // аа Обеспечение и рациональное использование энергетических и водных ресурсов в АПК: Материалы международной научно-практической конференции / Рос. гос. аграр. заоч. ун-т. М., 2009.- С.88-93.
Мамедов Ф.А., Денисов В.Н., Курилин С.П. .Линейные двигатели в высевающих аппаратах сеялок.//аа Обеспечение и рациональное использование энергетических и водных ресурсов в АПК: Материалы международной научно-практической конференции / Рос. гос. аграр. заоч. ун-т. М., 2009.-С.70-74.
аДенисов В.Н., Курилин С.П.а Диагностикаа асинхронныха электродвигателей с использованием импульсных функций// Вестник РГАЗУ. Научный журналаа а№7(12),МОСКВА 2009.-С.140-143.
Денисов В.Н., Курилин С.П.Сравнительный анализ энергосберегающего электропривода на основе линейных асинхронных двигателей// Ве?тник РГАЗУ. Научный журналаа а№8(13),МОСКВА 2010.-С.92-95.
Денисов В.Н., Курилин С.П. Исследованиеа энергосберегающего электропривода на основе линейных асинхронных двигателей// Энергообеспечение и энергосбережение в сельском хозяйстве. Труды 7-й Межд.научн.-техн. конференции ( 19-20 мая 2010 гд, г. Москва, ГНУ ВИЭСХ). в 5-ти частях. Часть 3. Энергосберегающие технологии в животноводстве и стационарной энергетике.
Денисов В.Н., Курилин С.П. Визуальные модели векторных пространств и проблемы энергосбереженияа .// Системы компьютерной математики и их приложения: материалы XI международной научной конференции, посвященной 70-летию профессора Дьяконова В.П.- Смоленск: изд-во СмоГУ,2010.-Вып. 11.-342 с.(С.45-46).
Денисов В.Н. О собственных колебаниях пластин в сыпучей среде. Энергетика, информатика, инновации -2011 ЦЭИИ-2011: сб. трудов Междунар. Научно-техн. Конференции. В 2 т.Т. 2. Смоленск:РИО филиала ГОУВПО МЭИ(ТУ) в г. Смоленске,2011.-С.49-51.

Патенты на изобретения и полезные модели:

Высевающий аппарат сеялки//Патент на полезную модель RU 88245 U1, F01Са 7/16, опубликован 25.03.2009 Бюл.№31. Мамедов Ф.А., Денисов В.Н.,Курилин С.П.
Вибрационная сушилка для сыпучих материалов// Патент RU а2377489а C1, F26B17/26, опубликован 27.12.2009, Бюл.№ 36аа Мамедов Ф.А., Денисов В.Н., Курилин С.П.
Высевающий аппарат сеялки// Патент на полезную модель RU 93621 U1, A01Са 7/16, опубликован 10.05.2010 Бюл.№13. Денисов В.Н., Курилин С.П.,Новиков В.М. Никитенков В.М.Швецова .
Роторный смеситель с электромеханическим вибровозбудителем// аа Патент на полезную модель RU 93696 U1, B01F 11/00, опубликован 10.05.2010 Бюл.№13. Денисов В.Н., Курилин С.П.
Роторный смеситель с механическим вибровозбудителем// Патент RUа 2398625 С1, B01F 11/00, опубликован 10.09.2010 Бюл. № 25. Денисов В.Н., Курилин С.П., Летов Л.А., Новиков В.М., Никитенков П.А.
Способ диагностики электрических двигателей с фазным ротором// Патент RUа 2392632а C1, G01Rа 31/34, опубликован 20.06.2010, Бюл.№ 17. Денисов В.Н., Курилин С.П.
аРоторный смеситель с электромеханическим вибровозбудителем// Патент на полезную модель RU 94165 U1, B01F 11/00, опубликован 20.05.2010 Бюл.№14. Денисов В.Н., Курилин С.П., Летов Л.А.
Многосекционная вибрационная сушилка.// Патент на полезную модель RU 105011 U1, F26B17/26 , опубликован
. Многосекционная вибрационная сушилка.// Патент на полезную модель RU 111620 U1, F26B17/26 , опубликован
Вибрационная сушилка для сыпучих материалов со встроенной электромеханической системой. .// Патент на полезную модель RU 112370 U1, F26B17/26 , опубликован 10.11.2012 Бюл.№ 1 . Денисов В.Н., Курилин С.П., Литвин В.И., Фицулин Д.А.
Вибрационная сушилка для сыпучих материалов со встроенной электро?еханической системой. .// Патент на полезную модель RU 112371 U1, F26B17/26 , опубликован 10.11.2012а аБюл.№ 1 . Денисов В.Н., Курилин С.П., Литвин В.И., Фицулин Д.А.
Вибрационная сушилкаа с конвейером для сыпучих материалов .// Патент на полезную модель RU 112372 U1, F26B17/26 , опубликован 10.11.2012 ааБюл.№ 1 . Денисов В.Н., Курилин С.П., Литвин В.И., Фицулин Д.А.

аа Личный вклад автора в опубликованные работы. Научные работы, представленные в диссертации, выполнены лично автором, под его научным руководством или при его активном участии. Участие автора выражено в разработке идей, постановке задач исследований, выборе научных направлений, разработке и исследовании математических моделей, разработке технических решений, их правовой защите, выполнении экспериментальных исследований, анализе и обобщении результатов. Все идеи, положения, научные результаты и выводы, приведенные в диссертации, получены автором. Работы [1,10,11,17,18,28,31,34, 35,37,38,41] выполнены автором лично. В работах [9,13,14,27,36,39,40,42-46, 48-59], участие автора выразилось в разработке основных научных аи практических идей. Доля участия автора в этих работах составляет 70 - 80%. В остальных работах участие автора выразилось в написании отдельных разделов объемом от 30 до а50%.

Автор выражает глубокую благодарность заслуженному деятелю науки РФ доктору технических наук, профессоруа Мамедову Фуаду Алиевичу аза научные консультации, всестороннюю помощь и поддержку при выполнении работы,а а доктору технических наук, профессору Курилину Сергею Павловичуа за конструктивное оппонирование при выполнении совместных исследований.

Объем 2,75 п.л. Тираж 100 экз.

Издательский центр филиала ГОУВПО МЭИ (ТУ) в г. Смоленске

214013, г. Смоленск, Энергетический проезд, 1.

Все авторефераты докторских диссертаций

Blog

Развитие теории и разработка вибрационных электромеханических систем сельскохозяйственного назначения