 Авторефераты по всем темам >>
Авторефераты по педагогике
Авторефераты по всем темам >>
Авторефераты по педагогике
МОДУЛЬНО-РЕЙТИНГОВАЯ ОЦЕНКА КАК СРЕДСТВО ПОВЫШЕНИЯ КАЧЕСТВА МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ СТУДЕНТОВ УНИВЕРСИТЕТА
Автореферат кандидатской диссертации по педагогике
![]()
На правах рукописи
Рязанова Любовь Сергеевна
Модульно-рейтинговая оценка как средство
повышения качества математического образования студентов университета
13.00.08 Ц теория и методика профессионального образования
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата педагогических наук
а
Магнитогорск
2010
![]() Работа выполнена на кафедре педагогики
Работа выполнена на кафедре педагогики
государственного образовательного учреждения
высшего профессионального образования
Магнитогорский государственный университет
Научный руководитель:
доктор педагогических наук, профессор
Савва Любовь Ивановна
Официальные оппоненты:
доктор педагогических наук, профессор
Романов Пётр Юрьевич
кандидат педагогических наук, доцент
Акманова Зоя Сергеевна
Ведущая организация:
ГОУ ВПО Челябинский государственный педагогический университет
Защита состоится л21 маяа 2010 года в 10 часов на заседании диссертационного совета Д 212.112.01 в Магнитогорском государственном университете по адресу: 455038, г. Магнитогорск, пр. Ленина, 114, ауд. 211.
С диссертацией можно ознакомиться в библиотеке Магнитогорского государственного университета. Текст автореферата размещен на сайте ГОУ ВПО Магнитогорский государственный университет
Автореферат разослан л19 апреля 2010 г.
Ученый секретарь
диссертационного совета,
доктор педагогических наук,
 профессораа Н.Я. Сайгушев
профессораа Н.Я. Сайгушев
ОБЩАЯ ХАРАКТЕРИСТИКА ИССЛЕДОВАНИЯ
Актуальность исследования. В условиях научно-технического прогресса категория качество рассматривается не только как ценность, самоцель, но и как мера сравнения объекта с заданным эталоном. Международный стандарт ISO а9000:2001 определяет качество как степень соответствия присущих объекту характеристик установленным требованиям. XXI век стал эпохой информационной революции, а знания и умение человека применять их - основными стратегическими ресурсами. Возрастает спрос на образовательные услуги, вместе с ним изменяются требования к их качеству. Интеграция России в европейское образовательное пространство актуализировала вопроса повышения качества высшего образования. По мнению В.А. Болотова, важным фактором повышения качества высшего образования выступает совершенствование контроля образовательного процесса. Вместе с тем, сохраняющиеся в образовании традиционные подходы к контролю не обеспечивают должного качества подготовки студентов. Поэтому одним из приоритетных направлений повышения качества образования в настоящий момент является применение в учебном процессе современных систем его контроля и управления.
Современные производственные технологии нуждаются в специалистах с высоким уровнем математической подготовки, владеющих не только классическими, но и новыми математическими методами. При этом многие учёные выражают озабоченность состоянием и перспективами математического образования в России (В.А. Садовничий, В.М. Тихомиров, И.Ф. Шарыгин и др.). Повышение качества математического образования актуально также в свете приоритетных направлений развития образовательной системы, одобренных Правительством Российской Федерации: улучшения качества профессионального образования, обеспечения его фундаментальности.
Различные аспекты математического образования освещены в широком круге научных работ. Целям, задачам, стандартам математического образования посвящены работы Б.В. Гнеденко, В.А. Садовничего, И.Ф. Шарыгина и др. Содержание математического образования стало объектом исследований аЕ.А. Москвиной, А.А. Прокофьева, Т.А. Шумеевой и др. В историческом аспекте математическое образованиеа рассматривается в работах В.М. Беркутова, З.У. Колокольниковой и др. Методике преподавания математики посвящены работы Ю.М. Колягина, Л.Д. Кудрявцева, В.М. Тихомирова и др. Анализ научных работ показал, что для математического образования, как и для профессионального образования в целом, актуально совершенствование контроля качества.
Эффективным средством повышения качества образования может служить введение в процесс профессиональной подготовки модульно-рейтинговой оценки, так как она стимулирует ритмичную работу студентов в течение семестра, их самоуправляемую деятельность, активизирует деятельность преподавателей (Ю.В. Белов, Н.В. Ефремова, С.И. Калачёва, Р.Я. Касимов, Н.Ю. Коробова, К.Л. Шхацева и др.). Однако, наряду с положительными результатами применения модульно-рейтинговой оценки, в практике вузов отмечены и негативные моменты: формальный подход преподавателя к проектированию модульно-рейтинговой программы, эмоциональное неприятие студентами рейтинговой оценки,а увеличение нагрузки преподавателя, создание ситуации погони за баллами, в ряде случаев отказ студентов от научно-исследовательской работы. Анализ опыта применения модульно-рейтинговой оценки привёл нас к выводу о том, что для устранения её негативных моментов и усиления позитивных сторон необходима разработка соответствующих педагогических и организационных мер.
Вышеизложенное позволяет выделитьа противоречия между:
возрастающими требованиями к качеству математического образования выпускников вуза и сохраняющимися традиционными подходами к контролю в образовательном процессе, не обеспечивающими должной математической подготовки студентов;
возможностью университетов в повышении качества математического образования студентов с применением модульно-рейтинговой оценки как педагогического средства и недостаточным уровнем теоретического обоснования и научно-методического обеспечения этого процесса.
Необходимость разрешения указанных противоречий определяет актуальность проблемы исследования, которая заключается в поиске и научном обосновании организационно-педагогических условий повышения качества математического образования студентов университета с применением модульно-рейтинговой оценки как средства.
Исходя из важности и актуальности данной проблемы, ее недостаточной теоретической и практической разработанности, была сформулирована тема диссертационного исследования: Модульно-рейтинговая оценка как средство повышения качества математического образования студентов университета.
Цель исследования - разработка и экспериментальная проверка модели повышения качества математического образования студентов университета с использованием модульно-рейтинговой оценки как педагогического средства.
Объекта исследования - математическое аобразование студентов в высшем учебном заведении.
Предмет исследования Ц повышение качества математического образования студентов университета с использованием модульно-рейтинговой оценки как педагогического средства.
Анализ литературы по теме и наш педагогический опыта позволили сформулировать следующую гинпотезу: повышение качества математического образования студентов университета возможно, если:
- определены структура, этапы, назначение модульно-рейтинговой оценки как основного педагогического средстваа повышения качества математического образования студентов вузов;
- разработана модель повышения качества математического образования студентов университета с применением модульно-рейтинговой оценки, которая основана на принципах модульного, личностно-ориентированного, компетентностного и задачного подходов;
- в рамках модели реализован следующий комплекс организационно-педагогических условий: а) осознание студентами объёма, содержания и выбора последовательности изучения материала в структурированном модуле; б) развитие творческой активности студентов в ходе решения комплекса задач разного уровня сложности; в) формирование ответственности студентов за результаты и своевременное выполнение учебных заданий;
- разработана и апробирована практико-ориентированная методика повышения качества математического образования студентов университета с применением модульно-рейтинговой оценки.
аЦель, предмет и гипотеза исследования предусматривают решение следующих задач:
Проанализировать состояние проблемы в педагогической теории и практике и определить понятийный аппарат исследования.
Уточнить структуру, этапы, особенности модульно-рейтинговой оценки как педагогического средства повышения качества математического образования.
Разработать структуру, содержание и связи модели повышения качества математического образования студентов университета с использованием модульно-рейтинговой оценки как основного педагогического средства.
Экспериментально проверить комплекс организационно-педагогических условий обеспечения эффективности разработанной модели.
Разработать и проверить эффективность практико-ориентированной методики повышения качества математического образования студентов университета с применением модульно-рейтинговой оценки.
Методологическую основу исследования составили: основные положения аличностно-ориентированного (В.А. Беликов, Э.Ф. Зеер,а Н.В.а Кузьмина,а А.Н. Леонтьев, А.К. Маркова, В.А. Петровский, А.В. Усова, К.Д. Ушинский, И.С. Якиманская и др.); модульного (Г.Н. Егорова, Х.М. Иннусова, Г.В. Лаврентьев, Н.Б. Лаврентьева, Д. Рассел, М.А. Чошанов П.А., Юцявичине, аН.М. Яковлева и др.); задачного (В. И. Андреев,а С. И. Архангельский,а аВ. В. Вербицкий, Ю. Н. Емельянов,а А. И. Зильберштейн,а ааТ.В. Кудрявцев,а аА. М. Матюшкин,а М. И. Махмутов,а Я. А. Пономарев,а М. Н. Скаткин,а ааВ. А. Сластенин,а В. П. Ушачев,а Г.И. Щукинаа и др.); компетентностного (А.Г.Бермус, Т.Е.Исаева, Л.И. Чумичёва и др.) подходов; исследования, посвященные различным аспектам проблемы профессиональной подготовки студентов (С.И. Архангельский, А.А. Вербицкий, Г.Г. Гранатов, М.Е. Дуранов, Л.М. Кустов, Р.А. Литвак, Л.М. Митина, А.Я. Найн, П.Ю. Романов, И.В. Резанович, А.Н. Сергеев, В.А. Сластёнин и др.); работы по педагогическому моделированию (С.И. Архангельский, В.П. Беспалько, Ф.И. Перегудов, Ф.П. Тарасенко, В.А. Штофф и др.).
Особое значение для нашего исследования имели работы, посвящённые различным аспектам математического образования (В.М. Беркутов, З.У. Колокольникова, Е.А. Москвина, А.А. Прокофьев, В.А. Садовничий, В.М. Тихомиров, И.Ф. Шарыгин и др.); исследованиям ааразличных аспектов педагогического контроля (В.П. Беспалько, П.Я. Гальперина, Е.П. Перовский, Н.Ф. Талызина и адр.); исследования, посвященные проблемам педагогического мониторинга, диагностики процесса и результата обучения, управления и оценки качества образования (В.С. Аванесов, Г.В. Ахметжанова, Т.Г. Калугина, Т.Е. Климова, Н.Г. Корнещук, Э.М. Коротков, А.Н. Майоров, Д.Ш. Матрос, Л.И. Савва, М.Б. Челышкова, Р.М. Чумичёва и др.); работы по изучению модульно-рейтинговой оценки качества образования (В. Алчинов, О. Боев, аР.Я. Касимов, Н.Ю. Коробова, В.В. Латынина, М. Панин, А. Чучалин, аК.Л. Шхацева и др.).
Базой исследования послужили Магнитогорский государственный университет, Магнитогорский государственный технический университет имени Г.И. Носова. В констатирующем эксперименте участвовало 139 студентов МГТУ имени Г.И. Носова и 198 студентов МаГУ. В формирующем эксперименте приняли участие 190 студентов МаГУ. Всего в экспериментальной работе участвовал 481 студент.
Цель и задачи определили логику и содержание теоретико-экспериментального исследования, которое осуществлялось с 2005 по 2010 в три этапа. На каждом этапе, в зависимости от решаемых задач и условий проведения работы, применялись соответствующие методы исследования.
Первый этап (2004 - 2007 г.г.). Целью данного этапа являлось изучение состояния проблемы повышения качества математического образования студентов университета средствами модульно-рейтинговой оценки. На данном этапе был проведён теоретический анализ философской, психолого-педагогической литературы; изучался и анализировался опыт применения модульно-рейтинговой оценки в высших учебных заведениях; определены предмет, объект и новизна исследования; составлен план опытно-экспериментальной работы, проведён констатирующий эксперимент. Ведущими методами исследования на данном этапе являлись: теоретический анализ литературы по проблеме исследования, анализ и обобщение педагогического опыта, анализ опыта высшей школы, наблюдение, констатирующий эксперимент, анкетирование, беседа, тестирование, опрос студентов и преподавателей вуза.
Второй этап (2007 - 2008 гг.).а Цель второго этапа - уточнение гипотезы исследования, разработка модели и педагогических условий повышения качества математического образования студентов университета с применением модульно-рейтинговой оценки. На данном этапе были выявлены структура, этапы, особенности данной оценки, разработана модель повышения качества математического образования студентов университета с её применением.а Основные методы исследования на данном этапе: методы теоретического моделирования, теоретический анализ, аметоды наблюдения, опроса, метод экспертных оценок, обобщение, систематизация, экспериментальная проверка.
Третий этап (2009 - 2010 гг.). Цель данного этапа - выявление комплекса организационно-педагогических условий повышения качества математического образования студентов университета с использованием модульно-рейтинговой оценки; проведение формирующего эксперимента; анализ и оценка результатов экспериментальной работы. Методы исследования на данном этапе: формирующий эксперимент, теоретический анализ, синтез, педагогический мониторинг, обобщение, объяснение, методы статистической обработки результатов, математические и графические методы.
Научная новизна выполненного исследования заключается в том, что:
- уточнены структура, этапы и особенности модульно-рейтинговой оценки как основного педагогического средства повышения качества математического образования студентов университета;
- разработана модель повышения качества математического образования студентов университета с использованием модульно-рейтинговой оценки, основанная на принципах модульного, личностно-ориентированного, компетентностного и задачного подходов, позволяющая объективно, оперативно, систематично и комплексно оценивать личностные и образовательные достижения студентов в течение и в конце семестра;
- выявлен, теоретически обоснован и экспериментально проверен комплекс организационно-педагогических условий повышения качества математического образования студентов университета ас применением модульно-рейтинговой оценки, направленный на: осознание студентами объёма, содержания и выбора последовательности изучаемого материала; развитие творческой активности и формирование ответственности студентов за результаты и своевременное выполнение учебных заданий;
- обоснована и экспериментально проверена практико-ориентированная методика повышения качества математического образования студентов университета с применением модульно-рейтинговой оценки, особенностью которой является поэтапная реализация комплекса организационно-педагогических условий.
Теоретическая значимость заключается в том, что результаты проведённого исследования вносят вклад в теорию профессионального образования и теорию качества образования, так как:
- уточнены признаки понятия модульно-рейтинговая оценка качества математического образования студентов университета;
- определены особенности применения принципов модульного, компетентностного, личностно-ориентированного и задачного подходов применительно к рассматриваемому процессу.
Практическая значимость исследования заключается в том, что:
- разработана модульная программа курсов Практикум на ЭВМ, аИнформатика с использованием модульно-рейтинговой оценки;
- разработаны и апробированы в вузах методические рекомендации для преподавателей и студентов: Модульно-рейтинговая система оценки качества образования, Модульно-рейтинговый контроль при преподавании гуманитарных дисциплин.
Материалы исследования могут быть широко использованы в педагогической практике вузов при внедрении в учебный процесс модульно-рейтинговой оценки, а также для оценки качества математического образования.
Достоверность и обоснованность полученных результатов исследования обеспечивается тщательным анализом философской, психолого-педагогической и методической литературы по проблеме; выбором комплекса методов, адекватныха предмету и задачама исследования, их методологической обоснованностью; разнообразием источников информации; репрезентативностью выборки контрольных и экспериментальныха групп; использованием методов математической статистики при обработке экспериментальных данных; подтверждением гипотезы; а также эффективными результатами внедрения методических разработока в практику вузов.
На защиту выносятся следующие положения:
- Компонентами модульно-рейтинговой оценки как педагогического средства повышения качества математического образования студентов университета являются рейтинговая оценка знаний и модульная организация образовательного процесса. Особенностями данной оценки выступают её объективность, систематичность и комплексность; направленность на коррекцию образовательного процесса, ритмичную учебную работу студентов,а развитие их навыков самообразования, самоорганизации и самоуправления; активизация субъектов образовательного процесса.
- аЭтапы модульно-рейтинговой оценки определены как проектирование модульной программы; внедрение рейтинговой оценки и коррекция образовательного процесса; вычисление рейтинга и итоговая аттестация.
- Модель повышения качества математического образования студентов университета с использованием модульно-рейтинговой оценки как педагогического средства состоит из четырёх взаимосвязанных компонентов: нормативно-целевого, организационно-содержательного, методического, оценочно-результативного; она основана на реализации принципов модульного, личностно-ориентированного, компетентностного и задачного подходов и позволяет объективно, оперативно, систематично и комплексно оценивать личностные и образовательные достижения студентов в течение и в конце семестра.
- Комплекс организационно-педагогических условий, направленный на повышение качества математического образования студентов университета с применением модульно-рейтинговой оценки, обеспечивает эффективное функционирование разработанной модели и включает в себя: а) осознание студентами объёма, содержания и выбора последовательности изучения материала в структурированном модуле; б) развитие творческой активности студентов в ходе решения комплекса задач разного уровня сложности; в) формирование ответственности студентов за результаты и своевременное выполнение учебных заданий.
- Практико-ориентированная методика повышения качества математического образования студентов университета с применением модульно-рейтинговой оценки включает совокупность специальных методов (тестирования, анкетирования, объяснения, анализа, синтеза, упражнения, наблюдения, рефлексивных методов), средств (основного: модульно-рейтинговой оценки и дополнительных: задач, заданий, дискуссий, диалога, тестов, анкет, правил, технических и электронных средств, рефлексивных заданий, вопросов) и форм организации обучения (практикумов, консультаций, групповой дискуссии, самостоятельной работы, контрольных работ, зачётов).
Апробация и внедрение результатов исследования осуществлялись посредством: публикаций в печати; отчётов на заседании кафедр педагогики, прикладной математики и вычислительной техники ГОУ ВПО Магнитогорский государственный университет; выступлений на методологических семинарах аспирантов и соискателей МаГУ (2005-2010 гг.). Материалы исследования излагались на международной научно-практической конференции Современные технологии оценки качества образования: модульно-рейтинговая система (г. Псков, 2006 г.), представлены в статьях журналов, рекомендованных ВАК для написания кандидатских диссертаций (Архангельск, 2006; Челябинск, 2008; Новосибирск, 2009 г.). Основные положения, выводы и рекомендации исследования, имеющие теоретическое и прикладное значение, содержатся в публикациях. Материалы диссертационного исследования прошли апробацию в ГОУ ВПО Магнитогорский государственный университет, Магнитогорский государственный технический университет имени Г.И. Носова.
Структура диссертации: диссертационная работа состоит из введения, двух глав, заключения, списка литературы по проблеме исследования.
Вовведении обосновывается актуальность проблемы исследования, определяются цель, объект и предмет исследования, формулируются гипотеза и задачи, обозначаются теоретико-методологическая основа и методы исследования, раскрываются научная новизна, теоретическая и практическая значимость исследования, характеризуются экспериментальная база и этапы исследования, представляются положения, выносимые на защиту, и приводятся сведения об апробации и внедрении результатов выполненной работы.
В первой главе - Теоретические аоснованияа повышения качества математического образования студентов университета с применением модульно-рейтинговой оценки - определяется разработанность заявленной проблемы в теории и практике высшего образования; даётся характеристика МРО как педагогического средства в повышении качества математического образования; разрабатывается модель повышения качества математического образования студентов университета с применением МРО; выявляется комплекс организационно-педагогических условий обеспечения её эффективности.
Во второй главе - Экспериментальная работа по повышению качества математического образования студентов университета с применением модульно-рейтинговой оценки - описывается логика и содержание педагогического эксперимента, методика использования МРО для повышения качества математического образования студентов университета; анализируются и обобщаются результаты экспериментального исследования.
В заключении изложены основные результаты и выводы исследования, намечены перспективы дальнейшего изучения проблемы.
ОСНОВНОЕ СОДЕРЖАНИЕ ДИССЕРТАЦИИ
- Теоретические основания повышения качества математического
- образования студентов университета средствами
- амодульно-рейтинговой оценки
Математическое образования сегодня является фундаментом для профессионального образования, различные его аспекты отражены в широком круге работ. Большинство исследователей рассматривают математическое образование как результат образовательного процесса, выделяя следующие его задачи: усвоение математических знаний; формирование математических умений; формирование репродуктивных и творческих способов математической деятельности и соответствующих качеств мышления. аМы, опираясь на аопределение В.М. Беркутова, рассматриваем математическое образование как результат процесса, направленного на формирование математических знаний, умений и опыта их творческой реализации.
Проведенный нами теоретический анализ показал, что существующие методологические подходы по-разному представляют содержание "качества образования". В рамках личностно-ориентированного подхода - это уровень развития личности; в культуросообразной модели образования его качество определяется как творчество личности; деятельностный подход под качеством образования понимает его результат: заданный объём знаний и умений; системный подход рассматривает качество как готовность выпускника одной образовательной системы к вхождению в другую.
Компетентностный подход диктует новые требования к определению качество образования, рассматривает его как результат процесса: наличие у выпускника вуза комплекса профессиональных компетенций, позволяющих ему адаптироваться к условиям современного производства и социума (Чумичёва). Компетенции определяются как результат профессиональной деятельности и условия обеспечения её качества. а
Совокупность математических знаний, умений, значимых качеств и ценностей личности мы рассматриваем как математические компетенции. Учитывая вышесказанное, качество математического образования студентов университетов мы понимаем как развитость их математических компетенций и сформированность опыта творческой деятельности.
Качество образования неразрывно связано с такими понятиями, как педагогический контроль, проверка, лоценка, лучёт результатов учебной деятельности. В педагогической литературе представлены различные точки зрения на определенияа и соотношение между собой данных понятий. Проведённый теоретический анализ позволил прийти к выводу о том, что под проверкой понимают процесс оценивания результатов обучения на определённом его этапе, а контроль определяют как систему проверочной деятельности. Оценка же рассматривается как определение и выражение в условных знаках-баллах, а также оценочных суждениях преподавателя степени аусвоения студентами знаний, умений, навыков. Вместе с тем, лоценку рассматривают и в более широком смысле: как процесс оценивания результатов учебной деятельности. В нашем исследовании, ориентируясь на компетентностный подход, лоценку мы понимаем акак систему проверочной деятельности, направленную на получение объективной и своевременной информации о степени развитости профессиональных компетенций и сформированности опыта творческой деятельности студентов.
Одним из видов педагогического контроля является кредитно-рейтинговый контроль, определённый Болонским соглашением как одно из условий достижения качества образования. Центральным понятием кредитно-рейтингового контроля является кредит - коэффициент атрудоёмкости дисциплины. аВ настоящее время в педагогической практике вузов введена система контроля, построенная на основе интеграции основных компонентов кредитно-рейтинговой системы: модульной организации образовательного процесса и рейтинговой оценки знаний - модульно-рейтинговаяа оценка (МРО) качества образования.
Теоретические основы и вопросы практического применения модульного обучения и рейтинговой оценки освещены в научной литературе. Модульная организация образовательного процесса подразумевает егоа разбиение на характеризующиеся своими целями организационно-методические структурные единицы учебной дисциплины - модули.аа Рейтинговая оценка качества освоения образовательной программы предполагает текущую оценку успешности познавательной деятельностиа студента в течение семестра и итоговую оценку в период сессии. Итоговый рейтинг определяется как процентное отношение полученного качества образования к запланированному, выраженных в баллах (формула 1):
(1)
а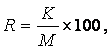
где ![]() а- итоговый рейтинг студента,
а- итоговый рейтинг студента, ![]() а- кумулятивный (накопительный) рейтинг студента,
а- кумулятивный (накопительный) рейтинг студента, ![]() а- запланированное качество образования, выраженные в баллах.
а- запланированное качество образования, выраженные в баллах.
В нашем исследовании мы рассматриваем МРО как педагогическое средство, поскольку данная оценка выступает средством аорганизации образовательного процесса и использует рейтинговую оценку как инструмент усвоения студентами математических компетенций, приобретения ими опыта творческой деятельности. Этапы МРО представлены как: 1) проектирование модульной программы; 2) внедрение рейтинговой оценки и коррекция образовательного процесса; 3) вычисление рейтинга и итоговая аттестация. Особенностями МРО выступают: 1) объективность, систематичность и комплексность оценки учебных достижений студентов; 2) направленность на коррекцию образовательного процесса, ритмичную учебную работу студентов, аразвитие их навыков самообразования, самоорганизации и самоуправления; 3) активизация субъектов образовательного процесса.
Нами уточнено, что модульно-рейтинговая оценка качества математического образования студентов университета - это атакая объективная, систематичная и комплексная оценка математических компетенций и опыта творческой деятельности студентов, полученных при освоении модульно-рейтинговой программы путём соотношения фактического качества образования и запланированного, которая позволяет своевременно осуществлять коррекцию образовательного процесса, стимулировать ритмичную работу и самоорганизацию обучающихся, развивать их навыки самообразования и самоуправления при педагогической поддержке преподавателя.
Исследования, проходящие в различных вузах, показали, что применение МРО как педагогического средства требует дальнейшего совершенствования и анаучного обоснования. В связи с этим мы пришли к выводу о необходимости моделирования процесса повышения качества математического образования студентов университета с применением МРО.
- 2. Модель повышения качества математического образования
студентов университета с применением модульно-рейтинговой оценки
В рамках нашего исследования мы выделяем три этапа моделирования: подготовительный этап, этап разработки модели, этап проверки её качества. Первый этап направлен на определение цели, объекта, методов и средств моделирования. Второй этап связан с разработкой и представлением модели, её описанием и характеристикой. Третий этап связан с экспериментальной проверкой её педагогических условий, методики в практике вуза и оценкой их эффективности. В работе представлено подробное описание каждого их выделенных этапов, остановимся на этапе разработки модели.
Модель повышения качества математического образования студентов университета с использованием МРО представлена четырьмя взаимосвязанными компонентами: нормативно-целевым, в состав которого входят социальный заказ, цель, задачи, а также принципы; организационно-содержательным, вбирающим модульно-рейтинговую программу курса Практикум на ЭВМ, комплекс педагогических условий, этапы МРО; методическим, содержащим методы, средства и формы; оценочно-результативным, включающим критерии, уровни и результат (рис. 1). Модель отражает требования, предъявляемые обществом к качеству математической подготовки студентов университета, основные идеи исследования, организацию процесса (цель, содержание, основные этапы МРО, педагогические условия, результат) и критерии оценки его эффективности. Рассмотрим компоненты представленной модели.
В состав нормативно-целевого компонента входят: социальный заказ, цель, задачи и принципы. Выявление социального заказа (высокий уровень математической подготовки специалистов в системе высшего профессионального образования) определило цель разрабатываемой модели как повышение качества математического образования студентов университета. По нашему мнению, данная цель может быть достигнута через решение следующих задач: 1) формирование у студентов университета математических знаний; 2) формирование у студентов университета репродуктивных математических умений в ходе решения типовых задач; 3) развитие действенности продуктивных и творческих математических умений в ходе решения нетиповых задач и задач-проблем; 4) формирование необходимых ценностей и личностных качеств.
Считаем, что модель основана на реализации принципов модульного, компетентностного, личностно-ориентированного и задачного подходов, а именно принципов: модульности, структуризации, ответственности, сознательности, рефлексивной активности, дифференцированности, индивидуального подхода, последовательности и преемственности в представлении задач. Данные принципы составляют основу нормативно-целевого компонента.
Организационно-содержательный компонент включает содержание, комплекс организационно-педагогических условий и этапы применения МРО. Элемент содержание содержит модульно-рейтинговую программу курса Практикум на ЭВМ для специальности Прикладная математика и информатика. В работе обосновано, что комплекс организационно-педагогических условий включает в себя: а) осознание студентами объёма, содержания и выбора последовательности изучения материала в структурированном модуле; б) развитие творческой активности студентов в ходе решения комплекса задач разного уровня сложности; в) формирование ответственности студентов за результаты и своевременное выполнение учебных заданий.
аМетодический компонент модели включает в себя: методы, средства и формы. Формами организации обучения были взяты практикумы, консультации, самостоятельная работа, групповые дискуссии, контрольные работы, зачёт.  В качестве методов были выбраны: тестирование, анкетирование, объяснение, анализ, синтез, упражнение, анаблюдение, рефлексивные методы. Основным педагогическим средством достижения цели разработанной модели в нашем исследовании выступает МРО качества математического образования студентов университета. Дополнительными педагогическими средствами являются правила, памятки, задачи, задания, тесты, анкеты, опросы, беседы, электронные и технические средства.
В качестве методов были выбраны: тестирование, анкетирование, объяснение, анализ, синтез, упражнение, анаблюдение, рефлексивные методы. Основным педагогическим средством достижения цели разработанной модели в нашем исследовании выступает МРО качества математического образования студентов университета. Дополнительными педагогическими средствами являются правила, памятки, задачи, задания, тесты, анкеты, опросы, беседы, электронные и технические средства.
Оценочно-результативный компонент включает обоснованные нами критерии, показатели, диагностические методики и результат. Нами выявлены низкий, средний, высокий уровни качества математического образования студентов университетов и дана их характеристика. Кроме того, в работе аргументировано, что данные уровни определяются следующими критериями и показателями: математическими знаниями (полнота и объём системы знаний, прочность знаний); математическими умениями (полнота сформированности умений, прочность умений, осознанность умений); опытом творческой деятельности (решение студентом типовых, нетиповых и творческих задач).
![]()
![]()
![]()
![]()
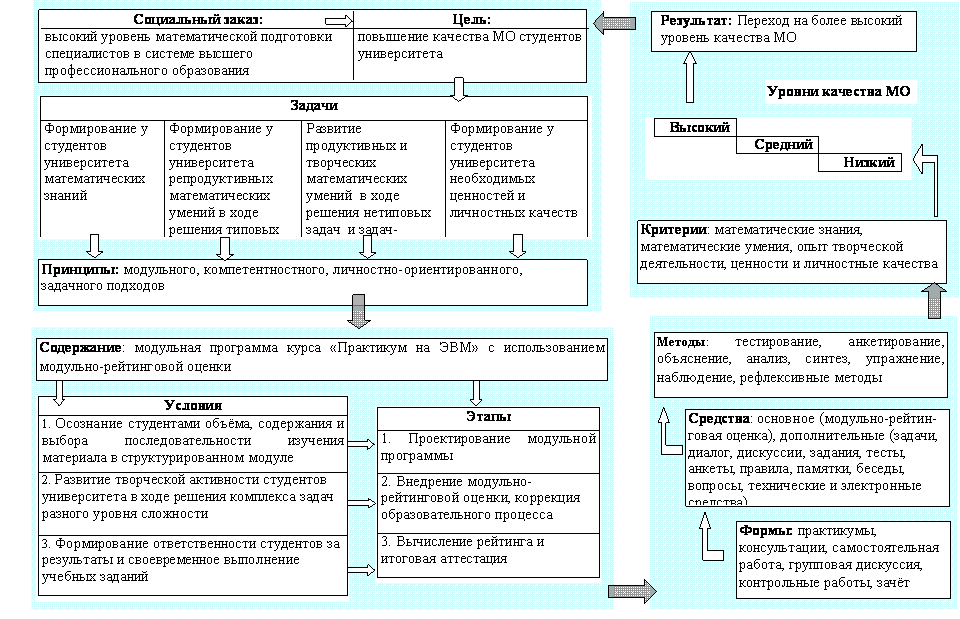
Рис.1. Структурная модель повышения качества математического образования (МО) студентов университета с применением МРО
Также к критериям качества математического образования мы отнесли ценности и личностные качества студентов (в качестве показателей определены: отношение студентов к математике, отношение студентов к оценке своего учебного труда, сформированность ответственности за результаты учебного труда, организованность студентов университета). Результат реализации модели сформулирован нами как переход студентов университетов на более высокий уровень качества математического образования.
Важно, что разработанная нами авторская модель имеет определенную закономерность. Все ее компоненты расположены последовательно: от нормативно-целевого до оценочно-результативного. Однако связь прослеживается не только между четырьмя компонентами модели, но и внутри каждого из них, обеспечивая продвижение от одного элемента к другому по указанному направлению. Определенная нами связь всех структурных составляющих компонентов и элементов в модели создаёт её целостность.
3. Комплекс организационно-педагогических условий обеспечения
эффективности модели повышения качества математического
образования студентов университета с применением
модульно-рейтинговой оценки
Реализация представленного комплекса условий велась на каждом из этапов МРО, при этом условия дополняли друг друга, но одно из них мы считали доминирующим, то есть необходимым на данном этапе, табл. 1. На этапе проектирования модульной программы доминирующим для нас являлось условие: осознание студентами объёма, содержания и выбора последовательности изучения материала в структурированном модуле. аНеобходимость введения данного условия обоснована тем, что проектирование модульной программы велось нами с учётом основных принципов модульного обучения: модульности и структуризации учебного материала.
Принцип модульности предполагает, что обучение строится по отдельным функциональным узлам (модулям), каждый из которых предназначен для достижения конкретной дидактической цели. Принцип структуризации учебного материала рассматривает учебный материал в рамках модуля не только как единое целое, но и как структуру, состоящую из обособленных и законченных элементов.
Структурирование учебного материала каждого модуля на взаимосвязанные и дополняющие друг друга теоретический, практический и творческий элементы помогает студентам осознать его объём и содержание. Это настраивает студентов на ритмичную учебную работу с начала семестра. Каждый из выделенных элементов модуля имеет свою цель: для теоретического элемента - ааэто формирование системы знаний, цель практического элемента - формирование математических умений, творческий элемента формирует готовность к творческой реализации накопленного потенциала. Данные цели взаимосвязаны и дополняют друг друга. Работа студентов с учебным материалом теоретического, практического и творческого элементов модуля может быть последовательной (в этом случае каждый предыдущий содержательный элемент готовит студентов к выполнению последующего) или параллельной, тогда акаждый из структурных элементов адресует студентов к материалу двух других элементов модуля.
Таблица 1
Особенности реализации комплекса организационно-педагогических
условий по этапам МРО
Условия
Этапы аМРО |
1. Осознание студентами объёма, содержания и выбора последовательности изучения материала в структурированном модуле |
2. Развитие творческой активности студентов университета в ходе решения комплекса задач разного уровня сложности |
3. Формирование ответственности студентов за результаты и своевременное выполнение учебных заданий |
Дополнительные педагогические средства |
|||
I. Проектирование модульной программы |
! Правила начисления балльной оценки, памятки, беседы, электронные и технические средства |
Правила начисления балльной оценки, памятки |
Правила начисления балльной оценки, памятки |
II. Внедрение рейтинговой оценки, коррекция образовательного процесса |
Правила начисления балльной оценки, памятки, электронные и технические средства, тесты |
! Задачи, диалог, рефлексивные задания и вопросы, дискуссии, правила начисления балльной оценки, опросы, памятки,а электронные и технические средства |
Правила начисления балльной оценки, памятки, беседы, рефлексивные вопросы, электронные и технические средства |
III. Вычисление рейтинга и итоговая аттестация |
Правила начисления балльной оценки, памятки, электронные и технические средства |
Правила начисления балльной оценки, рефлексивные вопросы, анкеты,а электронные и технические средства |
! Правила начисления балльной оценки, рефлексивные задания, вопросы, беседы, электронные и технические средства |
Примечание: знаком л! отмечено доминирующее условие на данном этапе МРО.
Дополнительными средствами на данном этапе были: правила начисления балльной оценки, памятки, беседы, электронные и технические средства.
На этапе внедрения МРО и коррекции образовательного процесса доминировало условие: развитие творческой активности студентов университетов в ходе решения комплекса задач разного уровня сложности. Данное условие направлено на развитие у студентов творческой активности и основано на принципах личностно-ориентированного и задачного подходов. Задачная технология реализована намиа за счёт представления элементов содержания образования в виде различного типа и уровня сложности задач. Классификация используемых задач представлена в работе. Личностно-ориентированный подход реализуется при выборе студентом уровня сложности решаемой задачи.
Анализ психолого-педагогической литературы показал, что лактивность трактуется как деятельное отношение человека к миру, его способность производить общественно-значимые преобразования материальной и духовной среды на основе освоения общественно-исторического опыта человечества, проявляющаяся в творческой деятельности, волевых актах и общении. Выделяют репродуктивную и творческую активность. Творческая активность определяется как высший уровень активности в учебно-познавательной деятельности. Развитие творческой активности осуществлялось нами путём решения студентами комплекса задач разного уровня сложности: типовых, нетиповых и творческих. Задачи разного уровня сложности (трудоёмкости) оценивались разным числом баллов. Количество баллов вычислялось нами путём применения коэффициента трудности (К) к количеству часов, отведённому в рабочей программе дисциплины на выполнение данного учебного задания, табл. 2.
Дополнительными педагогическими средствами на данном этапе применения МРО выступали: задачи, дискуссии, диалог, рефлексивные вопросы, тесты, электронные и технические средства, правила начисления балльной оценки, памятки.
На третьем этапе внедрения МРО (вычисление рейтинга и итоговая аттестация) доминирует третье условие: формирование ответственности студентов за результаты и своевременное выполнение учебных заданий. Данное условие основано на реализации принципов компетентностного подхода. Анализ психолого-педагогической литературы привёл нас к осмыслению того, что ответственность определяют как долг, моральное качество, профессиональную компетентность, ценность личности, выражающуюся в осознании себя как причины совершаемых поступков и их последствий,а в готовности взять на себя груз принятия решения и санкций за неудачу.
Если рассматривать ответственность как ценность личности, определяющую контроль её поведения, учения, образования, то правомерно утверждать, что качество обучения зависит от уровня ответственности студентов за процесс учения и его результат. Для поощрения своевременного выполнения учебных заданий студентами нами устанавливался срок сдачи для каждого учебного задания, были разработаны "штрафы" за несвоевременное его выполнение.
Каждое учебное задание в начале семестра оценивалось нами в баллах, назначалась дата его сдачи. Если студент сдавал работу на одно занятие позже указанного срока, то она оценивалась на 1 балл меньше, на два занятия - на два балла меньше, и т.д. Правила вычисления балльной оценки своевременноа разъяснялись студентам, в компьютерной сети размещались соответствующие памятки.
Опыт показал, что нецелесообразно уменьшать установленный балл более чем наполовину, независимо от срока задолженности, так как у студентов пропадает стимул выполнять просроченное задание. В процессе отслеживания результатов учебной деятельности студентов преподаватель фиксировал дату сдачи, качество выполненной работы. Таким образом, кумулятивный (накопительный) рейтинг задолжника был ниже, чем у студента, выполняющего все работы в срок. Эксперимент показал, что в начале следующего семестра студенты более активно включались в образовательную деятельность.
Таблица 2
Модульно-рейтинговая программа дисциплины Практикум на ЭВМ
|
Темы практических работ |
Бм |
Кол-во часов |
K |
Дата сдачи |
|||
Аудиторные |
Сам. работа |
Всего |
||||||
I мо д у л ь |
Практический блок |
|||||||
аЛабораторная работа Геометрические задачи |
8 |
8 |
0 |
8 |
1 |
16.02 |
||
абораторная работа Обработка последовательностей |
4 |
6 |
0 |
6 |
1 |
02.03 |
||
абораторная работа Задачи с целыми числами |
6 |
4 |
0 |
4 |
1 |
9.03 |
||
Теоретический блок |
||||||||
Теоретический тест по модулю |
4 |
2 |
|
2 |
2 |
14.03 |
||
Творческий блок |
||||||||
/р Решение задач |
10 |
0 |
5 |
5 |
2 |
|
||
Всего по модулю |
32 |
22 |
5 |
27 |
|
|||
II м о д у л ь |
Практический блок |
|||||||
абораторная работа Матрицы |
8 |
8 |
0 |
8 |
1 |
28.03 |
||
абораторная работа Системы счисления |
6 |
6 |
0 |
6 |
1 |
6.04 |
||
аЛабораторная работа Корни многочленов |
8 |
8 |
0 |
8 |
1 |
20.04 |
||
Теоретический блок |
||||||||
Теоретический тест по модулю |
3 |
2 |
|
2 |
1.5 |
25.04 |
||
Творческийа блок |
||||||||
/р Решение задач |
10 |
0 |
5 |
5 |
2 |
|
||
Всего по модулю |
35 |
24 |
5 |
29 |
|
|||
III м о д у л ь |
Практический блок |
|||||||
абораторная работа Логические формулы и фрагменты |
10 |
8 |
1 |
9 |
1.2 |
11.05 |
||
абораторная работа Рекурсия |
10 |
8 |
1 |
9 |
1.2 |
25.05 |
||
Теоретический блок |
||||||||
Теоретический тест по модулю |
3 |
2 |
|
2 |
1.5 |
30.05 |
||
Творческий блок |
||||||||
/р Решение задач |
10 |
|
5 |
5 |
2 |
|
||
Всего по модулю |
33 |
18 |
7 |
25 |
|
|||
|
Зачёт |
|
4 |
|
|
|
|
|
|
Количество часов в семестре |
|
68 |
17 |
85 |
|
||
Максимальный балл за семестр |
100 |
|||||||
Примечание: Бм аЦ максимальный балл, К - максимальный коэффициент трудности.
Дополнительными средствами на данном этапе были: правила вычисления балльной оценки, рефлексивные задания, вопросы, электронные и технические средства, беседа. Таким образом, представленная модель повышения качества математического образования студентов университета с применением МРО дополнена нами комплексом условий, особенностью реализации которого является последовательное применение на этапах данной оценки.
4. Основные результаты экспериментальной работы
Целью экспериментальной работы была проверка эффективности комплекса организационно-педагогических условий повышения качества математического образования студентов университета с применением МРО. Констатирующий этап эксперимента проводился на базе физико-математического факультета и факультета информатики Магнитогорского государственного университета, технологического факультета Магнитогорского государственного технического университета. В эксперименте участвовал 481 студент первого, второго, третьего и четвертого курсов.
Результаты, полученные на этом этапе эксперимента, позволили нам констатировать преобладание низкого и среднего уровней качества математического образования. На основании полученных данных, мы сделали вывод о необходимости применения новых педагогических средств в процессе повышения качества математического образования студентов университетов.
Общая выборка студентов формирующего эксперимента составила 190 студентов разных специальностей физико-математического факультета. Все респонденты были объединены в две экспериментальные и одну контрольную группу. В группе ЭГ-1 мы проверяли эффективность влияния двух выделенных условий, а именно: 1) осознание студентами объёма, содержания и выбора последовательности изучения материала в структурированном модуле; 2) формирование ответственности студентов за результаты и своевременное выполнение учебных заданий. В группе ЭГ-2 проверялась эффективность выделенных условий в комплексе. В контрольной группе К-1 МРО применялась без использования комплекса организационно-педагогических условий. Соответствующие данные представлены в табл. 3.
Результаты, представленные в табл. 3, убедительно свидетельствуют о том, что качество математического образования студентов возрастает при воздействии выделенного нами комплекса организационно-педагогических условий в двух экспериментальных группах.
Достоверность полученных результатов проверялась с помощью непараметрического критерия хи-квадрат. Нами была выдвинута нулевая гипотеза: разница по уровням качества математического образования студентов контрольной и экспериментальных групп статистически не значима, а также альтернативная гипотеза: уровень качества математического образования студентов контрольной и экспериментальных групп - не одинаковый, а различия существенны и не случайны.
Таблица 3
Данные по уровням качества математического образования астудентов университета на начало и конец формирующего эксперимента
Группы |
Уровни качества МО |
Кол-во человек группе |
|||||
Низкий |
Средний |
Высокий |
|||||
Кол-во |
% |
Кол-во |
% |
Кол-во |
% |
||
ЭГ-1 (Н) |
23 |
35,94 |
33 |
51,56 |
8 |
12,5 |
64 |
ЭГ-1 (К) |
6 |
21,98 |
47 |
62,50 |
11 |
15,63 |
64 |
ЭГ-2 (Н) |
25 |
39,68 |
32 |
50,79 |
6 |
9,52 |
63 |
ЭГ-2 (К) |
5 |
7,94 |
45 |
71,43 |
13 |
20,63 |
63 |
КГ (Н) |
23 |
36,51 |
33 |
52,38 |
7 |
11,11 |
63 |
КГ (К) |
17 |
26,98 |
38 |
60,32 |
8 |
12,70 |
63 |
Полученные нами расчетные данные показали в экспериментальных группах (ЭГ-1, ЭГ-2) на уровне значимости 0,05 преимущество альтернативной гипотезы перед нулевой, так как c2набл.>c2крит (7,81>5,99, 8,33>5,99) соответственно в ЭГ-1 и ЭГ-2.
Такой результат дал основание прийти к следующему выводу: повышение качества математического образования студентов университета не может быть объяснено случайными причинами, а является следствием введения комплекса педагогических условий. Так как наиболее высокие результаты были получены в группе ЭГ-2, был сделан вывод о том, что повышение качества математического образования студентов университета с применением МРО проходит более эффективно при введении всего комплекса организационно-педагогических условий.
Таким образом, положительные изменения в ходе формирующего эксперимента позволяют признать проведение экспериментальной работы достаточно успешным, а организационно-педагогические условия, обеспечивающие повышение качества математического образования студентов университета с применением МРО как средства необходимыми и достаточными.
В заключении изложены основные результаты и выводы исследования, намечены перспективы дальнейшего изучения проблемы.
Основные выводы исследования
- В ходе исследования было установлено, что проблема поиска и обоснования организационо-педагогических условий повышения качества математического образования студентов университета с использованием МРО как средства актуальна и требует дальнейшего теоретического осмысления.
- Компонентами модульно-рейтинговой оценки как педагогического средства повышения качества математического образования студентов университета являются рейтинговая оценка знаний и модульная организация образовательного процесса. Особенностями данной оценки выступают: объективность, систематичность и комплексность оценки учебных достижений студентов; направленность на коррекцию образовательного процесса, ритмичную учебную работу студентов,а развитие их навыков самообразования, самоорганизации и самоуправления; активизация субъектов образовательного процесса.
- Этапы модульно-рейтинговой оценки определены как проектирование модульной программы; внедрение рейтинговой оценки и коррекция образовательного процесса; вычисление рейтинга и итоговая аттестация.
- Уточнено, что модульно-рейтинговая оценка качества математического образования студентов университета - это атакая объективная, систематичная и комплексная оценка математических компетенций и опыта творческой деятельности студентов,а полученных при освоении модульно-рейтинговой программы путём соотношения фактического качества образования и запланированного, которая позволяет своевременно осуществлять коррекцию образовательного процесса, стимулировать ритмичную работу и самоорганизацию обучающихся, развивать их навыки самообразования и самоуправления при педагогической поддержке преподавателя.
- В работе обосновано, что модель повышения качества математического образования студентов университета с использованием МРО как средства, состоит из четырёх взаимосвязанных компонент: нормативно-целевого, организационно-содержательного, методического, оценочно-результативного; основана на принципах модульного, личностно-ориентированного, компетентностного и задачного подходов; позволяет объективно, оперативно, систематично и комплексно оценивать личностные и образовательные достижения студентов в течение и в конце семестра.
- Выявлено и доказано, что комплекс организационно-педагогических условий, направленный на повышение качества математического образования студентов университета с применением МРО, представлен в модели следующими условиями: 1) осознание студентами объёма, содержания и выбора последовательности изучения материала в структурированном модуле; 2) развитие творческой активности студентов в ходе решения комплекса задач разного уровня сложности; 3) формирование ответственности студентов за результаты и своевременное выполнение учебных заданий; реализация данного комплекса условий приводит к эффективному функционированию разработанной модели.
- Апробирована практико-ориентированная методика повышения качества математического образования студентов университета с применением МРО, вбирающая в себя: методы (тестирование, анкетирование, объяснение, анализ, синтез, наблюдение, упражнение, рефлексивные методы); средства (основные: модульно-рейтинговую оценку и дополнительные: задачи, дискуссию, диалог, атесты, анкеты, правила, технические и электронные средства, рефлексивные задания, вопросы); формы (практикумы, консультации, самостоятельную работу, групповую дискуссию, контрольные работы, зачёты).
- Обосновано, что повышение качества математического образования с использованием МРО - уровневый апроцесс. Критериями для определения уровня качества математического образования являются: математические знания, математические умения, опыт творческой деятельности, ценности и личностные качества.
- Проведённый статистический анализ полученных результатов экспериментальной работы показал, что выдвинутая гипотеза верна и цель исследования достигнута.
- аМы полагаем, что диссертационное исследование не исчерпывает всех аспектов обозначенной проблемы. Дальнейшая работа может быть посвященаа совершенствованию технологии учёта трудоёмкости различных видов учебной деятельности студентов при проектировании модульно-рейтинговой программы.
Основное содержание исследования отражено
в следующих публикациях автора:
- Рязанова, Л.С. Повышение качества математического образования как педагогическая проблема / Л.С. Рязанова // Сибирский педагогический журнал. - 2009. - № 7. - Новосибирск, 2009. - C. 51-56. (Реестр ВАК Минобрнауки РФ).
- Рязанова, Л.С., Шушкова, С.Н. Организационно-педагогические условия оценки качества математического образования студентов университетов / Л.С. Рязанова, С.Н. Шушкова // Сибирский педагогический журнал. - 2009. - № 2. - Новосибирск, 2009. - C. 303-311. (Реестр ВАК Минобрнауки РФ).
- Рязанова, Л.С. Модульно-рейтинговая система как средство повышения качества математического образования студентов университетов / Л.С. Рязанова // Вестник Челябинского государственного педагогического университета. - 2008. - № 10. - Челябинск, 2008. - С. 104-114. (Реестр ВАК Минобрнауки РФ).
- Рязанова, Л.С. Модульно-рейтинговая система как средство повышения качества образования / Л.С. Рязанова, М.В. Бишляга // Вестник Поморского университета. Серия Физиологические и психологические науки. - 2006. - № 7.а - Архангельск, 2006. - С. 43-49. (Реестр ВАК Минобрнауки РФ).
- аРязанова, Л.С.а Условия повышения эффективности применения модульно-рейтинговой системы оценки качества образования в вузе / Л.С. Рязанова, М.В. Бишляга // Современные технологии оценки качества образования: модульно-рейтинговая система: материалы V региональной научно-методической конференции (с международным участием). - Псков: Изд-во ПГПУ, 2006. - С. 41-43.
- Рязанова, Л.С. аОрганизационно-педагогические условия повышения качества математического образования студентов университетов в процессе применения модульно-рейтинговой системы / Л.С. Рязанова // Педагогические аспекты математического образования: сб. науч. тр. / под общ. ред. П.Ю. Романова. - 2008. - № 5. - Магнитогорск, 2008. - С. 99-101.
- Рязанова, Л.С. Методические рекомендации к применению модульно-рейтинговой системы оценки качества образования / Л.С. Рязанова // Современные технологии образования: сб. науч. тр. 6-й межрегион. заоч. науч.-практ. конф. / под ред. Т.Е. Климовой, Е.В. Романова. - 2006. - Магнитогорск, 2006. - С.138-140.
- Рязанова, Л.С.а Кредитно-рейтинговая система оценки качества образования её актуальность в современных условиях высшего образованияа / Л.С. Рязанова // Проблемы образования и развития личности учащихся: сб. науч. тр. докторантов, аспирантов, соискателей и преподавателей кафедры педагогики МаГУ / под ред. В. А. Беликова. - Магнитогорск: МаГУ, 2005. - С. 58-60.
- Рязанова, Л.С. Модульно-рейтинговая система оценки качества образования: Методические рекомендации для преподавателей и студентов / Л.С. Рязанова, М.В. Бишляга. - Магнитогорск: МаГУ, 2006. - 21с.
- Рязанова, Л.С. Модульно-рейтинговый контроль при преподавании гуманитарных дисциплин: Методические рекомендации для преподавателей и студентов / Л.С. Рязанова М.В. Бишляга. - Магнитогорск: МаГУ, 2006. - 22с.
![]()
Регистрационный № 0250 от 27.07.2006 г. Подписано в печать 15.04.2010 г.
Формат 60?841/16. Бумага тип № 1. Печать офсетная.
Усл. печ. л. 1,00. Уч.-изд. л. 1,00. Тираж 100 экз. Заказ № 279.
Бесплатно.
Издательство Магнитогорского государственного университета
455038, Магнитогорск, пр. Ленина, 114
Типография МаГУ
 Авторефераты по всем темам >>
Авторефераты по педагогике
Авторефераты по всем темам >>
Авторефераты по педагогике
