Упорядоченное (направленное) движение заряженных частиц
| Вид материала | Документы |
- Тс сила тока. Напряжение. Сопротивление. Закон Ома для участка цепи, 64.04kb.
- Самостоятельная работа Кредитная стоимость Лекции 36 Число недель, 154.88kb.
- Лабораторная работа №2 Моделирование движения небесных тел и заряженных частиц, 91.57kb.
- Изирующее излучение любое излучение, взаимодействие которого со средой приводит к образованию, 33.08kb.
- Молекулярная физика основы мкт изменение агрегатного состояния, 505.21kb.
- 01. 04. 20 – физика пучков заряженных частиц и ускорительная техника, 445.01kb.
- Фатихова Дания Ахтямовна, 249.42kb.
- «Проблемы теоретической и прикладной электронной и ионной оптики», 238.99kb.
- Спецификация темы «Тепловые явления» и примеры заданий к ней, 23.63kb.
- А. Н. Алмалиев, И. С. Баткин, М. А. Долгополов, И. В. Копытин, П. В. Лукин,, 70.09kb.
ЭДС в рамке, вращающейся в однородном магнитном поле. В проводнике, движущемся в постоянном магнитном поле, генерируется электрическое поле, возникает ЭДС индукции. Происходит преобразование механической энергии проводника в энергию электрического поля. С целью большей компактности генераторов электрического тока в электрическую энергию преобразуется механическая энергия вращательного дви-
24
Электродинамика

а)
*.j2>

б)
к 117
.зделение зарядов >амке, вращающейся шгнитном поле: а = 0; а = 90°
жения, а не поступательного. Основным элементом генератора является рамка, вращающаяся в магнитном поле. Во вращение рамку может приводить паровая машина, двигатель внутреннего сгорания, гидротурбина и т. д.
Найдем ЭДС, которая индуцируется в рамке со сторонами а и Ъ, вращающейся с угловой скоростью со в магнитном поле с индукцией В (рис. 117).
В начальном положении угол а, образуемый вектором индукции В с вектором площади AS, равен нулю (рис. 117, а). В этом положении рамки разделения зарядов не происходит.
В правой половине рамки вектор скорости со-направлен вектору индукции, в левой — направлен противоположно ему, поэтому сила Лоренца, действующая на заряды в рамке, равна нулю.
При повороте рамки на угол 90° в сторонах рамки под действием силы Лоренца происходит разделение зарядов (рис. 117, б). В сторонах 1 и 3 возникают одинаковые ЭДС индукции
а №2
fti = $а = vBb-Разделение зарядов в сторонах 2 и 4 незначительно, и поэтому ЭДС индукции, возникающими в них, можно пренебречь. С учетом того,
полная ЭДС, индуцируемая в рамке,
что v
равна
$t = 2$а = coBAS, (88)
где AS = аЪ.
ЭДС, индуцируемую в произвольном положении рамки в момент времени t, можно найти из закона Фарадея. Магнитный поток через площадь рамки изменяется с течением времени из-за изменения угла а = (at между линиями магнитной индукции и вектором площади:
Ф = BAScos со*. (89)
Тогда
£. = -
(90)
в6|
максимальная ЭДС, индуцируемая в рамке; $и
&BAS.
Электромагнетизм
125
| | (OBAS | Т = 2я/со | | |
| | | | | |
| 118 ЭДС индукции в рамке как функция времени | 0 -coBAS | я А Зге 2со со\ 2со | /2л 5л Зл\ /со 2со со \ | |
Гармоническая зависимость $t(t) приведена на рисунке 118. Частота ЭДС индукции V = - .
Генератор переменного тока. В генераторе переменного тока рамка вращается в магнитном поле, создаваемом постоянным магнитом. (В ряде конструкций рамка неподвижна, а вращается магнит.) Противоположные стороны рамки присоединены к кольцам, с которых с помощью гибких контактов (щеток) снимается индуцированный заряд. Принципиальное устройство генератора переменного тока показано на рисунке III на цветной вклейке, с. 257). Возникающий ток фиксируется осциллографом, а положения рамки показаны через каждую четверть периода ее вращения. При t = 0 и t = Г/2 заряды не разделяются, так как линейные скорости сторон рамки параллельны вектору магнитной индукции В. Когда t = Г/4 и t = ЗГ/4, разделение зарядов на сторонах рамки оказывается одинаковым, однако полярность сигнала, подаваемого на клеммы осциллографа, будет противоположной.
Для увеличения генерируемой ЭДС вместо рамки используют катушку с большим числом витков, называемую ротором. При подключении к щеткам нагрузки, потребляющей электроэнергию, через нее пойдет переменный ток, изменяющийся по гармоническому закону. Закон изменения тока в нагрузке зависит от того, какой элемент электрической цепи используется в качестве нагрузки.
ВОПРОСЫ
"■ Почему основным элементом генератора является рамка, вращающаяся в магнитном поле?
2. Поясните механизм разделения зарядов в сторонах рамки при ее вращении в магнитном поле.
*■ Нарисуйте один под другим графики зависимости от времени магнитного потока через вращающуюся рамку и ЭДС индукции в ней.
126
Электродинамика
- Объясните назначение гибких контактов (щеток) в генераторе переменного тока.
- Почему в реальном генераторе вместо рамки используют катушку с большим числом витков?
ЗАДАЧ И
- Прямоугольная рамка со сторонами а = 5смиЬ = 8см вращается вокруг вертикальной оси с периодом Т = 0,02 с в однородном магнитном поле с индукцией В = 0,$5Тл, направленной перпендикулярно оси вращения. Найдите максимальную ЭДС, индуцируемую в рамке, и зависимость ЭДС от времени. 'v[0i63 В]
- Найдите частоту вращения катушки с числом витков N = 20 в однородном магнитном поле с индукцией В - 0,5 Тл, если максимальная ЭДС в катушке fm = 7,85 В, а площадь сечения одного витка S = 25 см2. [50 Гц]
- Ротор генератора переменного тока, представляющий из себя катушку, содержащую N = 10 витков, каждый площадью S = 1200 см2, вращается с постоянной частотой у = 50Гц в магнитном поле с индукцией В = 0,58 Тл. Найдите максимальную ЭДС, индуцируемую в обмотке ротора. [220 В]
- При полете вертолета плоскость вращения его винта составляет с горизонтом угол а = 30°. Винт радиусом Д = 5м вращается с частотой v = 10 Гц. Найдите разность потенциалов между центром и краем винта. Вертикальная компонента магнитного поля Земли В = 5 • 10~4Тл. [nBvfi2sina = 0,2 В]
- Проводящая катушка с площадью поперечного сечения S = 100 см2 состоит из N = 200 витков и равномерно вращается с периодом Т = 20 мс в однородном магнитном поле с индукцией В = 0,2 Тл вокруг оси, перпендикулярной вектору магнитной индукции. Концы катушки замкнуты на резистор сопротивлением R = 100 Ом. Найдите, как изменяется сила тока через резистор со временем, определите частоту изменения силы тока и максимальное значение силы тока.
• \т _ 2nNBS _i ,R.l
итах--гд--1.26А]
§ 36. Передача электроэнергии на расстояние
Потери электроэнергии в линиях электропередачи. Электроэнергия производится вблизи источников топлива или гидроресурсов, в то время как ее потребители находятся повсеместно. Поэтому возникает необходимость в передаче электроэнергии на большие расстояния. При большой длине линии электропередачи ее электрическое сопротивление становится значительным. Это приводит к существенным потерям передаваемой мощности в подводящих проводах, пропорциональной сопротивлению
Электромагнетизм
127
линии г. Согласно формуле (46) потери мощности в подводящих проводах
составляют
Р2 Р = — г
" U2 '
где Р — мощность источника тока (генератора), U — передаваемое напряжение.
Оценим мощность, теряемую в подводящих проводах.
Крупный город потребляет электрическую мощность порядка 20 МВт. Из-за потерь мощности электростанция должна вырабатывать существенно большую мощность. Сопротивление 1 км двухпроводной линии из
медного провода диаметром 1 см равно: г1 = р- =1 Ом. Тогда при переда-
че электроэнергии при напряжении 200 В потери мощности на 1 км подводящих проводов составляют:
Рп =
При передаче на расстояние 1000 км потери мощности составят 1010кВт. За 1 ч в подводящих проводах потери составляют 1010кВт • ч. При стоимости одного киловатт-часа 2 р. потери оцениваются в 20 млрд р./ ч. Значительно уменьшить сопротивление линии практически невозможно. Поэтому уменьшение потерь мощности в линиях электропередачи (ЛЭП) достигается за счет повышения передаваемого напряжения. Потери мощности обратно пропорциональны квадрату передаваемого напряжения. Например, электроэнергия от Самарской ГЭС в Москву передается при напряжении 400 кВ. При таком напряжении потери энергии и их стоимость уменьшаются по сравнению с предыдущим вариантом в
(400-103t л ("loo-J =4млнРаз-
Поэтому передача электроэнергии на расстояние требует сначала повышения напряжения с 20 кВ до 400—500 кВ, а затем его снижения до 220 В, сравнительно безопасно используемых потребителем. Подобное изменение напряжения — технически затруднительная проблема при передаче постоянного тока, которая практически отсутствует в линиях электропередачи переменного тока. Это определяет повсеместное применение ЛЭП переменного тока, в которых изменение напряжения осуществляется с помощью трансформаторов.
Схема передачи электроэнергии потребителю. Рассмотрим принципиальную схему передачи электроэнергии от генератора к потребителю
128 Электродинамика

Генератор ЛЭП высокого Промышленное Потребитель
электростанции напряжения предприятие
▲ 119
Принципиальная схема передачи электроэнергии на расстояние и ее распределения
(рис. 119). Обычно генераторы переменного тока на электростанциях вырабатывают напряжение, не превышающее 20 кВ, так как при более высоких напряжениях резко возрастает возможность электрического пробоя изоляции в катушке (обмотке) и в других частях генератора.
Для сохранения передаваемой мощности (снижения потерь мощности) напряжение в ЛЭП должно быть максимальным, поэтому на крупных электростанциях ставят повышающие трансформаторы. Однако напряжение в линии электропередачи ограничено: при слишком высоком напряжении между проводами возникают разряды, приводящие к потерям энергии.
Для использования электроэнергии на промышленных предприятиях требуется значительное снижение напряжения, осуществляемое с помощью понижающих трансформаторов. Дальнейшее снижение напряжения до величин порядка 4 кВ необходимо для энергораспределения по местным сетям, т. е. по тем проводам, которые мы видим на окраинах городов. Менее мощные трансформаторы снижают напряжение до 220 В (напряжение, используемое большинством индивидуальных потребителей).
В России и странах ЕС (Европейского сообщества) используется переменное напряжение с частотой 50 Гц. Такой эталон частоты выбран с учетом инерционности человеческого зрения, позволяющего различать сигналы длительностью не менее 0,05 с. Частота 50 Гц достаточна для того, чтобы человеческий глаз не замечал изменения интенсивности излучения ламп накаливания.
Электромагнетизм
129
ВОПРОСЫ
•j. Почему повышение напряжения, передаваемого в линии электропередачи, уменьшает потерю мощности в подводящих проводах?
- Для чего в линиях электропередачи используют повышающие трансформаторы?
- Чем ограничено повышение напряжения в линиях электропередачи?
- Зачем при передаче электроэнергии на расстояние используют понижающие трансформаторы?
- Почему в качестве частоты переменного напряжения используется частота 50 Гц?
§ 37. Векторные диаграммы для описания переменных токов и напряжений
Представление гармонического колебания на векторной диаграмме.
Переменное напряжение, получаемое потребителем от электростанции через ЛЭП, изменяется с течением времени по гармоническому закону.
Мгновенное значение напряжения — напряжение в данный момент времени t можно представить в виде:
и = Umcos (cot + ф0), (91)
где Uт — амплитуда (максимальное значение) напряжения, со — круговая частота колебаний, равная угловой скорости вращения ротора генератора электростанции.
Аргумент косинуса ф = Ш + tp0 определяет фазу колебаний в момент времени t.
Фаза колебаний — аргумент функции, описывающей гармонические колебания.
и = Umcos(mt + <р0)

При заданной амплитуде фаза определяет yj мгновенное значение колеблющейся величины. Начальная фаза колебаний ф0 — фаза колебаний в начальный момент времени, т. е. при t = 0.
Для наглядного описания гармонических колебаний используется метод векторных диаграмм. В методе векторных диаграмм гармоническое колебание представляют в виде вектора. А 120 Модуль этого вектора равен амплитуде колеба- Представление гармо-нии, а угол, образуемый вектором с осью X, ра- нического колебания вен начальной фазе колебаний (рис. 120). Воз- в виде вектора
В. А. Касьянов, 11 кл.
130
Электродинамика

Фо=0
t = OX
то синусоидальное колебание можно представить в виде вектора длиной 1т, направленного противоположно оси У. Этот вектор имеет начальную фазу (-л/2) (рис. 121,6).
Рассмотрим теперь вращение вокруг начала координат вектора с модулем Um, имеющего начальную фазу ф0 (рис. 122, а). При угловой скорости вращения со его проекция на ось X изменяется по закону Umcos (со* + ф0).
Косинусоидальное колебание Umcos (со* + ф0) представляется в виде вектора длиной Um, составляющего с осью X угол ф0 (рис. 122, б). Синусоидальное колебание можно выразить как косинусоидальное:
а)
| Y | | | | |
| | Л, sin т | со* | t= | 0 |
| О | со* "" | Ч; | | X |
| 1т | 1 | ,-' | Фо = | я 2 |
б)
121
Векторная диаграмма
для:
я) косинусоидальных
колебаний;
б) синусоидальных
колебаний
можность такого представления гармонического колебания следует из взаимосвязи гармонического колебательного движения с вращением по окружности (см. Ф-10, § 18).
Рассмотрим подробнее эту взаимосвязь, чтобы обосновать метод векторных диаграмм. Предположим, что вектор с модулем 1т в начальный момент (* = 0) направлен по оси X. Если определить начальную фазу ф0 как угол, образуемый вектором с осью X в начальный момент времени, то ф0 = 0. Пусть этот вектор вращается в плоскости XY с угловой скоростью со против часовой стрелки (рис. 121, а). Через время * вектор поворачивается на угол cot.
Проекция вектора 1т на ось X изменяется по косинусоидальному закону Imcos со*. Поэтому косинусоидальное колебание удобно представить в виде вектора длиной 1т, направленного по оси X, т. е. имеющего начальную фазу, равную нулю. Любое синусоидальное колебание можно рассматривать как косинусоидальное с определенной начальной фазой. Так как
(*-!>
(92)
/„sin со* = /mcos
Umsm (со* + ф0) = Umcos (со* + ф0 - | ],
(93)
н поэтому представить вектором длиной Um, составляющим с осью X угол р0 - 7с/2. Этот угол играет роль начальной фазы для этого вектора. При наличии двух гармонических колебаний
Электромагнетизм
131
(94)
их = Umlcos ((at + фх)
«2 = Um2COS № + Фа)
их разностью фаз Д(р = <р2 - Ф! на векторной диаграмме является угол между ними (рис. 123). Говорят, что второе колебание опережает первое по фазе на Аф или что первое колебание отстает по фазе от второго на Аф. Такая терминология связана с тем, что векторы вращаются против часовой стрелки.
Сложение двух колебаний. Сложение колебаний на векторной диаграмме происходит по правилу сложения векторов, т. е. по правилу параллелограмма или треугольника.
Рассмотрим сложение двух колебаний с одинаковой амплитудой Um:
иЛ = Umcos (at,
ТТ • / 5)
и 2 = Umsin (at.
Найдем сначала результат сложения этих колебаний аналитически:
(-!))■
и1 + и2
U„ I cos со* + cos
cos
2C/mcos I
Следовательно,
(96)
"l + "2 = Um 2 cos ((at - j ].
Тот же результат легко получается с помощью векторной диаграммы (рис. 124). Косинусои-Дальному колебанию соответствует вектор с модулем Um, направленный по оси X, так как ф0 = 0.
Второе колебание можно тоже записать через косинус с начальной фазой (-л/2):
"2 = «COS ((at - | У
•этому колебанию соответствует вектор с моду-ем ш' направленный противоположно оси У, так как ф0 = л/2.
5*

0 Umcos(a>t + %) Х а)
у
 | Umcos(a>t + %)
| Umcos(a>t + %)иA Umsin((ot + %) б)
▲ 122
Колебания с начальной фазой на векторной диаграмме:
а) косинусоидальные;
б) синусоидальные
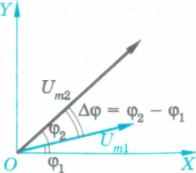
А 123
Разность фаз двух гармонических колебаний
)
Электродинамика

Сложение векторов дает вектор с модулем Umj2 и начальной фазой (-л/4). Такое колебание описывается зависимостью (97).
ВОПРОСЫ
1.
124
жжение колебаний на ;торной диаграмме
Дайте определение мгновенного значения напряжения, фазы колебаний и начальной фазы колебаний.
Как гармоническое колебание представляют на векторной диаграмме?
Как изображаются на векторной диаграмме косинусо-идальное и синусоидальное колебания?
Как изображаются на векторной диаграмме два синхронных колебания?
Как происходит сложение колебаний на векторной диаграмме?
ЗАДАЧИ
Напряжение меняется с течением времени по закону и = 10cos (2п/Т) (t + Г/6) В.
Найдите амплитуду, круговую частоту, начальную фазу и мгновенное значение на
пряжения в момент времени t = Т/4. [10В; 2к/Т; я/3; -8,5 В]
Изобразите на векторной диаграмме гармоническое колебание силы тока
i = 4cos(10< + 3rc/4)A.
Изобразите на векторной диаграмме гармоническое колебание напряжения и = 6sin (Ы - л/3) В.
Какое из двух колебаний u, = 10cos (cot + л/4), и2 = 10sin (cot + л/4) отстает по фазе?
Чему равно это отставание? Покажите его на векторной диаграмме. [я/2]
Сложите на векторной диаграмме колебания, описанные в задаче 4. Запишите за
кон результирующего колебания. [14,14 cos rot]
38. Резистор в цепи переменного тока
ла тока в резисторе. Предположим, что в качестве нагрузки генератора >еменного тока используется резистор с сопротивлением R (рис. 125, а), пряжение, созданное генератором на концах резистора, изменяется по :ону
и = Umcos (ot. (97)
В соответствии с законом Ома сила тока в резисторе будет
(98)
U
- д = Jmcos со*,
m ~ Um/R — амплитуда силы тока.
Электромагнетизм
133
б> и\1 Г=2я/ш 1
а)
J
 ) Ун
) УнR
cos cot
fcH
£/_
J
0 X
A 125
Резистор в цепи переменного тока:
а) схема включения; б) изменение со временем напряжения и силы тока;
в) векторная диаграмма
Напряжение и сила тока в резисторе синхронно меняются с течением времени по косинусоидальному закону (рис. 125, б).
Напряжение и сила тока в резисторе совпадают по фазе в любой момент времени. На векторной диаграмме (рис. 125, в) векторы Um и 1т, имеющие нулевую начальную фазу, направлены по оси X.
Действующее значение силы переменного тока. При включении в цепь переменного тока амперметра, рассчитанного на измерение постоянного тока, его стрелка будет колебаться с частотой 50 Гц. Поэтому определить величину тока, меняющегося в пределах от -1т до +1т, будет практически невозможно. Напомним, что сила тока 1 А была введена как сила постоянного тока (см. § 25). Возникает вопрос: какой переменный ток эквивалентен по действию постоянному току 1 А?
Среди известных действий электрического тока — химического, магнитного и теплового, только тепловое действие не зависит от изменения направления тока. Тепловая мощность, выделяемая в резисторе, пропорциональна квадрату силы тока (см. (44)): Р = PR.
Сила переменного тока 1 А — сила тока, выделяющего в проводнике такое же количество теплоты, что и постоянный ток 1 А за тот же промежуток времени.
Амперметр переменного тока измеряет действующее значение силы тока.
Действующее значение силы переменного тока равно силе постоянного тока, при котором в проводнике выделяется такое же количество теплоты, что и при переменном токе за тот же промежуток времени.
134 Электродинамика
Если переменный ток изменяется по гармоническому закону, в качестве промежутка времени выбирается период изменения тока. Чтобы найти действующее значение силы тока, протекающего через резистор, воспользуемся выражением для мгновенной мощности тока, выделяемой в резисторе:
P. = i2R= /2Rcos2cot.
Учитывая, что cos2 Ш — - (1 + cos 2(ot), получаем:
Р.=
ilR
IlR
+
(99)
cos cot.
2 2
Графиком зависимости мгновенной мощности тока от времени является косинусоида с амплитудой J2 R/2, периодом Г/2 = я/со. Косинусоида сдвинута вверх по вертикальной оси на IR/2 (рис. 126).
Равенство количества теплоты, выделяемого за период переменным и постоянным током, означает равенство средних тепловых мощностей этих токов. Из рисунка 126 видно, что средняя мощность Р_, выделяемая за период переменным гармоническим током, равна
IlR
Такая же мощность Р= выделяется в резисторе при протекании постоянного тока 1Д:
Действующее значение силы переменного тока получается, если приравнять эти мощности:
0,5/<Д
(
 100)
100) 126 ►
Мгновенная тепловая мощность, выделяемая в резисторе за период изменения силы тока
Электромагнетизм
135
Действующее (эффективное) значение силы, переменного гармонического тока в J2 раз меньше его амплитуды. Аналогично определяется действующее (эффективное) значение переменного гармонического напряжения:

(101)
U ш —2
и* Л'
В цепях переменного тока резистор часто называют активным сопротивлением.
Активное сопротивление — сопротивление элемента электрической цепи, в котором электрическая энергия необратимо преобразуется во внутреннюю.
Активным сопротивлением обладают электролампы, электродвигатели, трансформаторы и т. д.
ВОПРОСЫ
- Как связаны между собой напряжение и сила тока в резисторе?
- Что означает выражение: «Сила переменного тока в 1 А»? Почему сравнивают именно тепловое действие переменного и постоянного тока?
- Дайте определение действующего значения переменного тока.
- Как связано действующее значение силы тока (или напряжения) с его амплитудным значением?
- Какое сопротивление в цепи переменного тока называют активным?
