Лекция №4. Модели данных > Лекция №4. Модели данных Вопросы организации данных в гис, в частности, модели структуры данных, форматы, одна из самых сложных, самых важных и определяющих тем в гис

Вид материала

Лекция

Содержание 4.11. Модели представления графической информации. 4.12.Квадратомическое дерево

Подобный материал:

• Лекция 1) гис как специализированная информационная система. Структура информационных, 78.1kb.
• Курс лекций "Базы данных и субд" Ульянов В. С. Лекция. Манипулирование реляционными, 276.31kb.
• Лекция №3. Организация данных в гис первым шагом к проекту гис является создание пространственной, 268.29kb.
• Возможности реляционной модели данных по отображению сложных структур данных, 155.27kb.
• Проектирование базы данных, 642.58kb.
• Программы для интерпретации гис интегрированнaя система обработки данных гис "прайм", 103.04kb.
• Программа дисциплины Системы управления базами данных Семестры, 22.73kb.
• Реляционные решения: от открытия реляционной модели данных до проблематики фундаментальных, 61.83kb.
• Гис-технологии в экологии, 1013.18kb.
• Дискретных Марковских Цепей) в анализе данных. Пример применения. (лекция, 7.29kb.

4.11. Модели представления графической информации.

Не менее важным является деление моделей данных на векторные. оперирующие непосредственно с координатами объектов и слагающих его точек и модели данных с делением пространства. где положение объекта или слагающего его элемента задается принадлежностью к некоторому дискрету, элементу делимости пространства. Наиболее распространенным видом моделей с делением пространства являются растровые модели данных, то есть использующие регулярную сетку точек или, что эквивалентно, разбиение пространства на регулярные ячейки прямоугольной (чаще квадратной) формы. Однако хочется подчеркнуть, что хотя их практическое значение и распространенность гораздо больше, чем у других моделей данных с делением пространства, вся эта группа очень разнообразна и представляет значительный теоретический интерес. Отдельные на первый взгляд экзотические модели данных из этой группы находят довольно неожиданное применение в комбинации с векторными и растровыми данными. Например, с их помощью могут строиться системы пространственного индексирования.






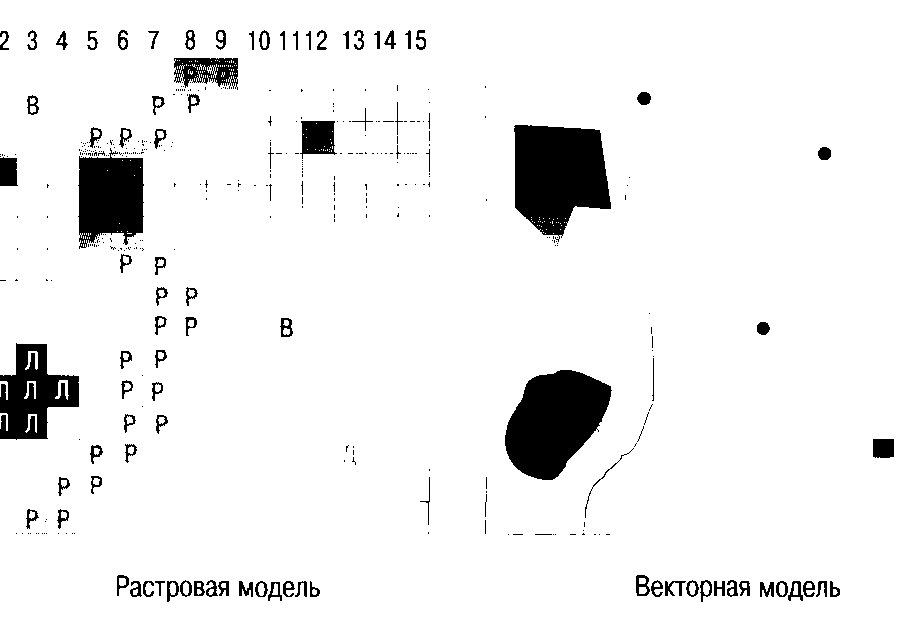
Серьезные ГИС сегодня также должны обладать возможностями работать с непрерывно распределенными данными, что часто заставляет в одной системе использовать комплексные (часто говорят, гибридные) модели данных (то есть фактически несколько разных моделей данных). Все это делает ГИСовские модели данных и форматы в среднем более сложными, чем все остальные. Можно думать, что и передний край теоретического осмысления общих вопросов о моделях и форматах данных также сегодня проходит в области геоинформатики.

Если вернуться только к области ГИС, то все равно сохраняется подразделение моделей и форматов данных по типу использования. Я говорю о моделях и форматах внутренних (реально используемых системой при ее основном функционировании) и моделях и форматах обменных, предназначенных для обмена с другими (ГИСовскими и неГИСовским пакетами).

4.12.Квадратомическое дерево

Иерархическая структура данных, известная как квадратомическое дерево, используется для накопления и хранения географической информации. В этой структуре двухмерная геометрическая область рекурсивно подразделяется на квадраты, что определило название данной модели.

На рис. 3.8 показан фрагмент двухмерной области QT, состоящей из 16 пикселей. Каждый пиксель обозначен цифрой. Вся область разбивается на четыре квадранта: А, В, С, D. Каждый из четырех квадрантов является узлом квадратомического дерева. Большой квадрант QT становится узлом более высокого иерархического уровня квадратомического дерева, а меньшие квадранты появляются на более низких уровнях.

Технология построения квадратомического дерева основана на рекурсивном разделении квадрата на квадранты и подквадранты до тех пор, пока все подквадранты не станут однородными по отношению к значению изображения (цвета) или пока не будет достигнут предопределенный заранее наименьший уровень разрешения.

Если регион состоит из 2n х 2n пикселей, то он полностью представлен на уровне n, а единичные пиксели находятся на нулевом уровне. Квадрант уровня 1 (0<1
На рис. 3.9 показано квадратомическое дерево, построенное по данным рис. 3.8. Как видно, эта структура являет собой классический пример Е-дерева. Преимущество такой структуры состоит в том, что регулярное разделение обеспечивает накопление, восстановление иобработку данных простым и эффективным способом. Простота проистекает из геометрической регулярности разбиения, а эффективность достигается за счет хранения только узлов с данными, которые представляют интерес.






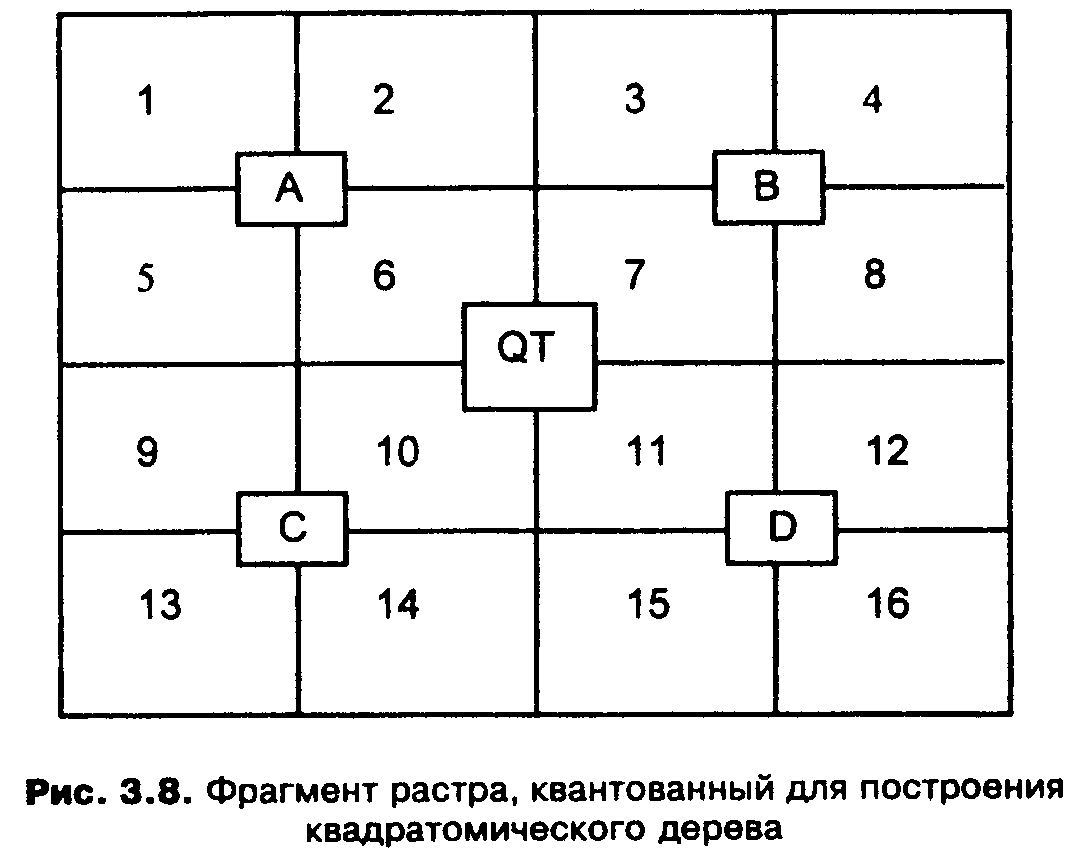
Рис. 3.8. Фрагмент растра, квантованный для построения квадратомического дерева





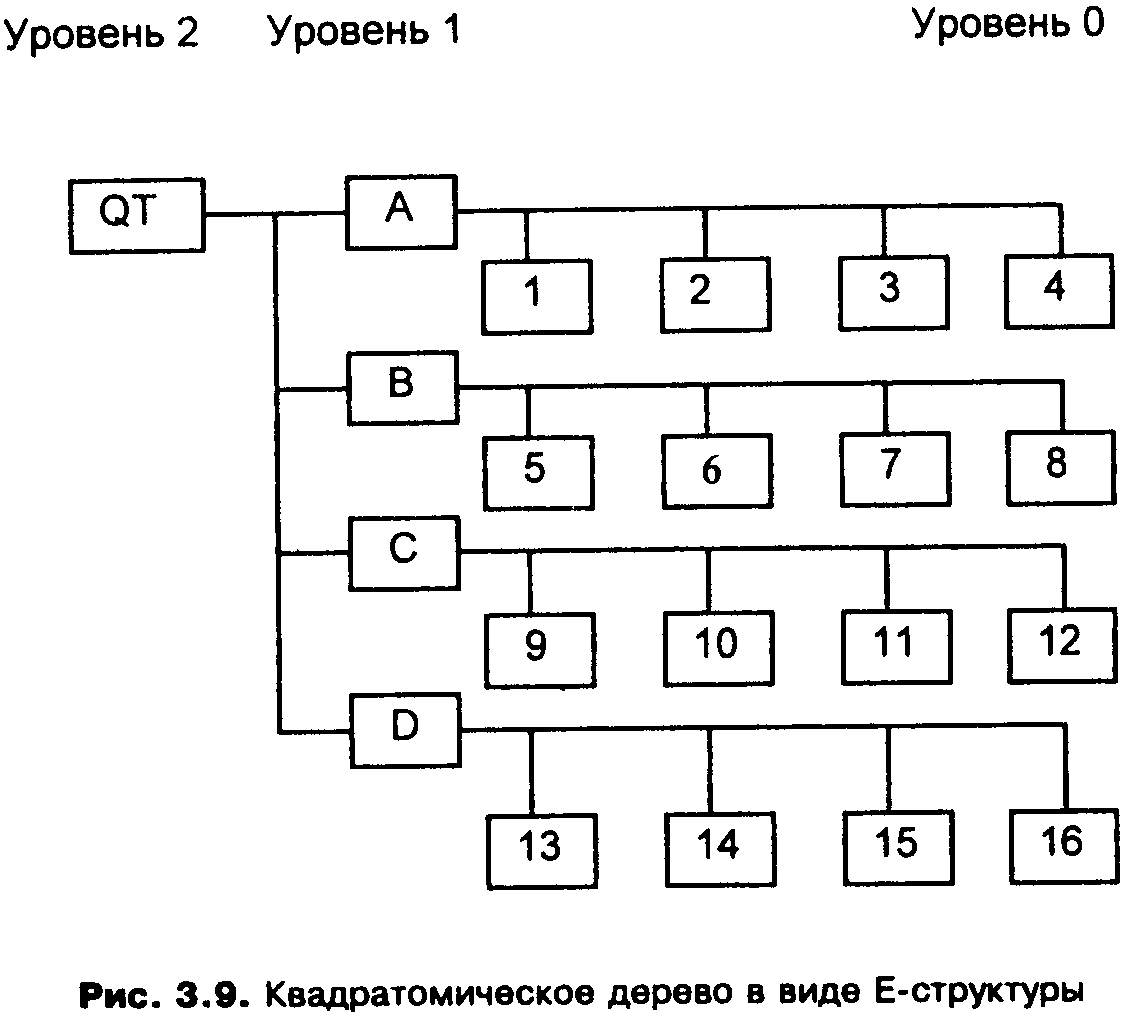
Рис. 3.9. Квадратомическое дерево в виде Е-структуры

Поскольку квадратомическое дерево известно как пространственно-рациональный способ представления сгруппированных однородных ми сопряженных изображений, их преимущество над векторной репрезентацией многих (но не всех) пространственных алгоритмов относительно затрат машинного времени весьма существенно.

Первоначально большинство приложений моделей квадратомических деревьев было сделано для обработки изображений. Из этой области данная модель была перенесена в ГИС.

Модели, основанные на квадратомических деревьях, обеспечивают расчеты площадей, центроидные определения, распознавание образов, выявление связанных компонентов, определение соседства, преобразование расстояний, разделение изображений, сглаживание данных и усиление краевых эффектов. Вследствие этого появилась возможность использовать квадратомические деревья для хранения географических данных. Однако при этом требуется развитие процедур для превращения растровых данных в формат квадратомического дерева и усовершенствование техники линейного кодирования.

Во-первых, работах по квадратомическим деревьям связи между квадрантом и подквадрантом давались в виде дерева со степенью ветвления, равной четырем. В такой структуре связи между родительским и дочерним уровнем определяются системой внешних указателей.

Все узловые точки дерева, за исключением корневой, имеют одного родителя. В то же время все они, за исключением листьев, связаны с четырьмя дочерними узловыми точками.

Преимущество представления, основанного на указателях, заключается в том, что оно выражает только значимую часть полного квадратомического дерева.

Последние исследования показали, что для больших квадратомических деревьев наиболее подходящей структурой является линейное квадродерево. В нем каждый листовой узел представлен линейным числовым кодом, который базируется на упорядоченном списке узловых точек прародителей. Последующее преобразование дерева в код достигается использованием битового уровня или модулярной арифметики. Система линейных кодов обеспечивает эффективную связь между структурами пространственных данных и алгоритмами, применяемыми в вычислительной геометрии для решения проблем восстановления прямоугольников и определения ближайшего "соседа".

Рядом исследователей была рассмотрена возможность использования искусственного интеллекта для совершенствования очень больших географических информационных систем, основанных на квадратомических деревьях.

Иерархические модели, как и прочие, могут описывать системы, данные и схемы процессов обработки данных. Следует, однако, подчеркнуть, что правильно составленная иерархическая схема должна содержать в качестве записей ( вершин) атрибуты или агрегаты атрибутов либо типы сущностей. Атрибуты или агрегаты атрибутов соответствуют множествам или расширенным множествам. Дуги могут использоваться для представления агрегации двух атрибутов в тип сущности или двух типов сущности в тип связи. На практике часто в запись вставляют не только сущности базы данных, но и связи. Такая схема описывается моделью "сущность-связь" и будет рассмотрена ниже.

Анализ иерархических моделей (связей между их частями) с "неправильным" описанием необходимо проводить, выделяя типы сущностей.