Geum.ru

Лекция №4. Модели данных > Лекция №4. Модели данных Вопросы организации данных в гис, в частности, модели структуры данных, форматы, одна из самых сложных, самых важных и определяющих тем в гис

Вид материалаЛекция

Содержание


4.6. Формы представления непрерывных признаков - полей.
Нерегулярная сеть точек
TIN (Triangulated Irregular Network)
Подобный материал:
1   2   3   4   5   6   7   8

4.6. Формы представления непрерывных признаков - полей.


Некоторое свойство, непрерывно распределенное в пространстве, например, на земной поверхности, удобно в математическом смысле рассматривать в качестве поля. (Вообще говоря, разного вида -скалярного, векторного, тензорного, трехмерного или двумерного, определенного только на поверхности земли или с ней не связанного, а только проектируемого на нее или пересекаемого ею, но всех сложностей мы сейчас касаться не будем). Типичные формы представления подобных непрерывных свойств таковы:

Н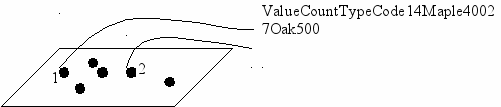ерегулярная сеть точек - произвольно расположенные точечные объекты, в качестве атрибутов имеющие значение поля в данной точке. С помощью такого способа представления, если не иметь очень густо расположенных по сравнению с пространственной изменчивостью поля точек, трудно гарантировать его адекватное представление. Сеть может быть слишком редкая, или точки, выбранные случайно, не попадают на характерные представительные места/значения, или, наоборот, точки выбраны неслучайно и тоже не являются представительными (например, все значения кислотности почвы измерялись только там, где можно было легко передвигаться по местности, то есть на голых водоразделах, а не в заболоченных речных долинах).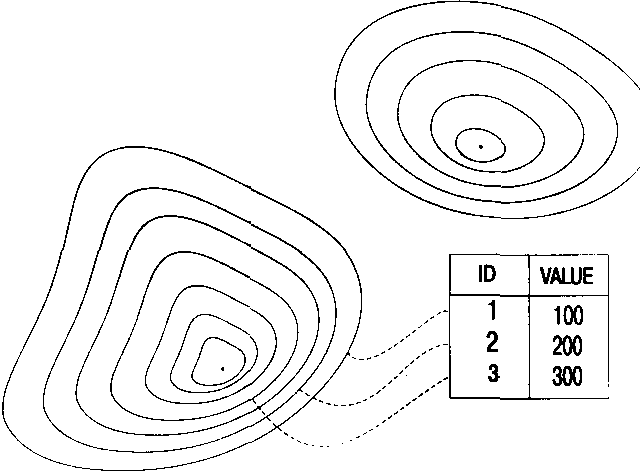





Способ представления изолиниями - наиболее распространен в традиционной картографии. Обычно нет никакой информации о поведении поля между изолиниями, и вторая проблема состоит в том, что по одним и тем же исходным данным (обычно это точки нерегулярной сети) интерполяция и последующее проведение изолиний может быть сделана не единственным способом. Способ представления очень привычный, но не самый удобный для анализа.


Наиболее удобен для многих случаев вариант, когда поля задаются регулярно расположенными в пространстве точками достаточной густоты (регулярная модель), особенно когда это точки не интерполированные из нерегулярных, а измерения, проведенные по регулярной сети. Из них легко перейти к любой другой форме представления.

1

2

Value
Count
Type
Code

1
4
Maple
400

2
7
Oak
500


















Несколько особняком стоит модель данных TIN (Triangulated Irregular Network), специально предназначенная для представления поверхностей значений, полей (например и в первую очередь -поверхности рельефа местности). Это также нерегулярная сеть точек, но точек связанных, соединенных особым образом выбранной сетью прямых отрезков, при этом эти отрезки (называемые часто ребрами - edges) образуют множество треугольников, как бы грани (фасеты). Наличие таких связок между точками дает некоторое представление (линейное приближение) о поведении поля (или форме поверхности) на данном участке в промежутке между точками. Поэтому модель данных типа TIN часто позволяет получать более качественное и более экономное представление поверхностей (полей). В особенности удачным оказывается применение этой модели данных для ситуации, когда изменчивость поля (например, рельефа местности) очень разная в разных частях территории, например, если район изучения захватывает и горный район, и плоскую предгорную равнину. К сожалению, многие типы аналитических задач трудно выполнимы на этом типе модели данных.




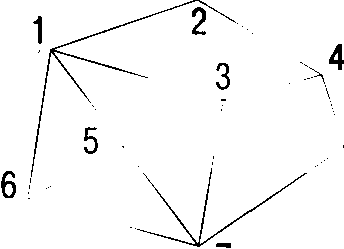
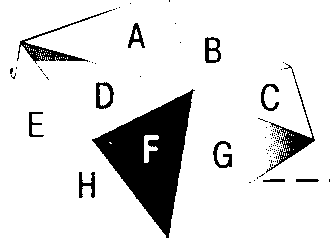
Треугольник
Список точек
Соседи

А
1,2,3
-,B,D

B
2,4,3
-,C,A

C
4,8,3
-,G,B

D
1,3,5
A,F,E

E
1,5,6
D,H,-

F
3,7,5
G,H,D

G
3,8,7
C,-,F

H
5,7,6
F,-,E