Элективный курс «Математика и гармония окружающего мира»

Вид материала

Элективный курс

Содержание Б. Рассел Тематическое планирование курса Урок №1 Тема урока План проведения урока Бертран Рассел Легко отыскать примеры прекрасного, но как трудно объяснить, почему они прекрасны. Платон Симметрия…есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство. План проведения урока Домашнее задание Цель урока Circle (x, 240), 50, 14 План проведения урока Window (-16,-12) – (16,12) Бенуа Мандельброт и его теория фрактальных кривых. Домашнее задание План проведения урока Слайд 20) Цель урока Леонардо да Винчи Цель урока ... Полное содержание

Подобный материал:

• Липецка Учитель Тарасова Светлана Васильевна. Предмет математика. Класс 9 элективный, 242.74kb.
• Элективный курс 11 класс «методы научного познания и физическая картина мира» (авторская, 107.2kb.
• Элективный курс «Уравнения и неравенства с модулем» 10 класс разработан учителем моу, 93.7kb.
• Элективный курс "Музыка мира: джаз" Пояснительная записка Элективный курс "Музыка мира:, 177.75kb.
• Элективный курс " Лексика и фразеология" Пояснительная записка, 71.55kb.
• Конспект урока окружающего мира в 3 классе умк «Гармония», 90.12kb.
• Кирилина Лидия Ивановна 2008 Содержание Введение 3 История математики на урок, 220.88kb.
• Элективный курс «глобальные проблемы человечества», 121.74kb.
• В. А. Ходаков моу воротынская средняя школа Перемышльского района Калужской области, 76.7kb.
• Элективный курс по астрономии, 93.86kb.

Элективный курс

«Математика и гармония

окружающего мира»





Разработчики:

Константинова Т.Г. – учитель математики и информатики

Строганов К., Аванян П. – учащиеся 11 класса


Программа элективного курса

«Математика и гармония окружающего мира»


Математика владеет не только истиной, но и высшей красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.

Б. Рассел


Данный элективный курс рассчитан на 17 часов (одно полугодие). Его слушателями могут быть учащиеся 10 или 11 классов. Программа данного курса предусматривает знакомство учащихся с законами математики, которые присутствуют в окружающем мире, управляют этим миром. Главной целью данного курса является попытка сформировать у учащихся убеждение в том, что математика, искусство и красота – понятия неразделимые. Математика – это царица всех наук, её красоте, мудрости, стройности и гармонии можно только бесконечно удивляться и восхищаться ею. Искусство – это точное соблюдение законов математики, гармония, пропорциональность, творческое вдохновение, художественное мастерство. Законы математики действуют даже в тех областях, где их менее всего ожидалось встретить: в живописи, музыке, скульптуре. И тем не менее, это так. Данный курс призван познакомить учащихся и убедить их в справедливости этого положения. Думается, что изучение этого курса позволит шире взглянуть на окружающий мир, ещё и ещё раз поразиться неразрывному сочетанию науки и искусства, пополнить свой багаж знаний. В ходе изучения курса учащиеся познакомятся с большим количеством иллюстративного материала, это станет возможным путём использования составленных к этому курсу набору презентаций. В ходе обучения предполагается выполнения практических работ в среде QuickBasic, работа в сети Интернет, работа с тестирующими программами. Итогом всей работы будет создание общего сетевого проекта: «Искусство, наука, красота».


Тематическое планирование курса

«Математика и гармония окружающего мира»

№ урока	Тема урока	ЦОР
1	Введение. Математика и искусство	Презентация
2	Удивительный мир симметрии	Презентация
3	Орнаменты, бордюры, паркеты	Презентация
4	Построение орнаментов и бордюров	Quick Basic
5	Замечательные кривые	Quick Basic
6	Красота фракталов	Презентация
7	Перспектива- геометрия живописи.	Презентации
8	Перспектива в изобразительном искусстве	Презентации
9	Пропорция. Тайны Золотого сечения.	Презентация
10	Золотые пропорции в природе, живописи, скульптуре	Презентация
11	Математика архитектурной гармонии	Презентация
12	Пифагор и пифагорейское учение о числе	Презентация
13	Математический строй музыки	Презентация
14	Пять красивых тел. Правильные многогранники	Презентация
15	Итоговое тестирование	Tester
16-17	Создание сетевого проекта «Искусство, наука, красота».	PowerPoint Internet

Урок №1

Тема урока: Математика и искусство.

Цель урока: показать учащимся неразрывную связь между основными законами математики и законами построения произведений искусства.

План проведения урока


1.Урок – лекция. Лекция сопровождается показом презентации.

Тезисы лекции учителя.

В природе существует много такого, что не может быть ни достаточно глубоко понято, ни достаточно убедительно доказано, ни достаточно умело и надёжно использовано на практике без помощи вмешательства математики.

Ф.Бэкон

Едва ли кто-нибудь из нематематиков в состоянии освоиться с мыслью, что цифры могут представлять собой культурную или эстетическую ценность или иметь какое-нибудь отношение к таким понятиям, как красота, сила, вдохновение. Я решительно протестую против этого костного представления о математике.

Н.Винер

Математика, Гармония, Красота.

Гармония означает «согласованность, соразмерность, единство частей и целого, обуславливающие внутреннюю и внешнюю формы предмета, события, явления, их совершенство». Внешне гармония может проявляться в мелодии, ритме, симметрии, пропорциональности.

Математика – царица всех наук, символ мудрости. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства. Это не только стройная система законов, теорем и задач, но и уникальное средство познания красоты.

Красота многогранна и многолика. Она выражает высшую целесообразность устройства мира, подтверждает универсальность математических закономерностей, которые действуют одинаково эффективно в кристаллах и живых организмах, в атоме и во Вселенной, в произведениях искусства и в научных открытиях

Конечно же, все законы красоты невозможно вместить в несколько формул. Но, изучая математику мы открываем всё новые и новые слагаемые прекрасного, приближаясь к пониманию, а в дальнейшем и к созданию красоты и гармонии. Искусство, наука, красота… эти великие сферы человеческой деятельности, внешне столь разные и далекие друг от друга, тесно переплетены между собой незримыми узами! И разорвать эти узы нельзя, не повредив и тому и другому. Красота является самым крепким связующим звеном между наукой и искусством!

«Потребность красоты и творчества, воплощающего ее, - неразлучна с человеком, и без нее человек, быть может, не захотел бы жить на свете».

Ф. М. Достоевский

Добро, Истина, Красота. Древние утверждали триединство этих трёх ликов культуры. Со временем Истина отошла к науке, Красота к искусству, а Добро вообще повисло в воздухе. Но наука, не освящённая идеалами Добра, ведёт мир к катастрофе. Искусство, потерявшее луч Истины, погружается в мир декаданса. Красота в равной мере должна питать искусство и науку. «Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства».

Бертран Рассел

Математик, так же как и художник или поэт, создает узоры, и если его узоры более устойчивы, то лишь потому, что они составлены из идей.

Легко отыскать примеры прекрасного, но как трудно объяснить, почему они прекрасны.
Платон

«Математика есть прообраз красоты мира».

В.Гейзенберг

Очень важно найти математические закономерности в прекрасном - «законы красоты». Попытки хотя бы приблизиться к ним предпринимались с древнейших времён: это и математические законы Пифагора в музыке, и геометрическая модель Вселенной Кеплера, это и система пропорций в скульптуре и архитектуре, и геометрические законы живописи. И сегодня энтузиазм исследователей не убывает.

В отличие от истины красота понятна человеку даже тогда, когда её внутренние закономерности остаются непознанными. Каждый ясно видит разницу между правильными и неправильными чертами человеческого лица, но до сих пор никто не может точно сформулировать закон, которому подчинена форма красивого лица. Струи бьющих фонтанов привлекают правильностью и красотою своих линий, хотя не каждый знает, что это параболы, и тем более не в состоянии написать их уравнения.

Существуют ли объективные законы прекрасного?

• Нельзя отрицать заглавную роль симметрии в природе, которая обязана своим существованием вечному закону природы - закону тяготения.
  
• В основе основ музыки и архитектуры- гамме и пропорции – лежит математика, в частности ряд золотого сечения и модулор Ле Корбюзье.
  
• В изобразительном искусстве используется общая теория перспективы.
  

Однако не стоит наводить «математический » порядок в искусстве. Искусство живёт своей жизнью, оно соткано из диалектически противоположных начал – материального и духовного, рационального и иррационального, сконструированного и сотворённого рассчитанного и угаданного. В первом случае искусство доступно точному математическому анализу, во второй неподвластно математике, да и не нужно разрушать эту волшебную часть искусства логикой. Искусство – это не только содержание , но и форма. Но не убьёт ли знание законов формообразования искусство, не превратит ли его в процесс изготовления штампов? Истинному искусству это не грозит. Имхотеп и Хесира, Поликлет и Пракситель, Дюрер и Леонардо да Винчи, Моцарт и Бах, Палладио и Ле Корбюзье – все они отдали дань поиску математических законов искусства, однако это не убило в них художников, а скорее наоборот, помогло стать великими.

Единство науки и искусства – важнейший залог последующего развития культуры


Домашнее задание.

Подготовить сообщение с демонстрацией примеров в виде презентации на тему: «Единство науки и искусства»


Литература

1.А.И.Азевич «Двадцать уроков гармонии» библиотека журнала «Математика в школе», выпуск 7. Москва «Школа-Пресс», 1998год

2. А.В. Волошинов «Математика и искусство», Москва, «Просвещение»,

1992 ГОД

3. CD “ Microsoft Office at school”

4. И.Ф.Шарыгин, Л.Н. Ерганжиева «Наглядная геометрия 5-6 классы» Москва, Издательский дом «Дрофа», 1998 год.

5. DVD Tsarskoe selo Master Video, 2004


Урок №2

Тема урока: Удивительный мир симметрии.

Цель урока: познакомить учащихся с симметрией – основополагающим принципам устройства мира.

План проведения урока


Рассказ учителя. Демонстрация презентации «Удивительный мир симметрии»


Симметрия…есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство.

Герман Вейль

Симметрия является фундаментальным свойством природы, представление о котором слагалось в течение десятков, сотен, тысяч поколений. В древности слово «симметрия» употреблялось в значении «гармония», «красота». Действительно, в переводе с греческого это слово означает «соразмерность, пропорциональность, одинаковость в расположении частей ». «Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство» - отмечал Г.Вейль. Симметрия принадлежит к числу широко и повсеместно распространённых явлений. Её всеобщность служит эффективным инструментом познания природы. Симметрия в природе – следствие необходимости сохранять устойчивость. Симметрия лежит в основе законов сохранения. Можно сказать, что симметрия – это проявление стремления материи к надёжности и прочности.

Будем называть симметрией фигуры любое преобразование, переводящее фигуру в себя, т.е. обеспечивающее её самосовмещение.

В школьном курсе геометрии рассматриваются три вида симметрии.

• симметрия относительно точки (центральная симметрия);
  
• симметрия относительно прямой (осевая или зеркальная симметрия);
  
• симметрия относительно плоскости.
  

Эти виды симметрии человек встречает повсюду: в природе и кристаллографии, архитектуре и живописи, скульптуре и народном творчестве.

Однако наряду с привычными формами симметрии существуют и другие виды симметрии.

• Винтовая симметрия. Например, рассматривая расположение листьев на ветке дерева, видим, что один лист не только отстоит от другого, но и повёрнут вокруг оси ствола. Листья располагаются на стволе по винтовой линии.
  
• Знакомое понятие и параллельного переноса используются при определении так называемой переносной симметрии.
  
• Понятие поворота даёт представление о поворотной симметрии. Например, пятиконечная звезда, будучи повёрнута на 72⁰ (360⁰: 5), займёт первоначальное положение.
  

Таким образом, не только симметричные формы окружают нас повсюду, но и сами биологические и физические законы пронизаны общим для всех них принципом симметрии. Принцип симметрии в ХХ веке охватывает всё новые области. Из области кристаллографии, физики твёрдого тела он вошёл в область химии, в область молекулярных процессов, в физику атома.

Симметрия многолика. Она обладает свойствами, которые одновременно и просты, и сложны. Даже человек, мало знакомый с геометрией, легко выберет из предложенных фигур наиболее симметричные Например из всех треугольников самый симметричный –равносторонний, из всех четырёхугольников – квадрат.

Разносторонний треугольник можно перевести в себя единственным способом: повернув всю плоскость на 360⁰ вокруг какой-нибудь точки. Такое отображение называется тождественным и обозначается Е. Равнобедренный треугольник может быть отражён сам в себя с помощью преобразования (Е) и осевой симметрии относительно высоты, проведённой к основанию (S). А вот у равностороннего треугольника можно уже насчитать шесть симметрий. Е, S1,S2,S3, повороты относительно точки О на 120⁰ и 240⁰.

Большинство четырёхугольников могут быть отображены на себя только преобразованием Е. Ромб можно совместить с самим собой с помощью Е, двумя S относительно диагоналей и относительно центра О.Самый богатый симметриями является квадрат, у него их – восемь: Е, относительно О,S1,S2 относительно диагоналей,S3,S4 относительно серединных перпендикуляров к сторонам квадрата, повороты вокруг точки О на 90⁰ и 270⁰.

А теперь спросим себя: какая из фигур нам нравится больше? Скорее всего это будет или правильный треугольник или квадрат. Человек инстинктивно стремится к устойчивости, удобству, красоте. Наверное, поэтому нам кажутся более привлекательными фигуры, у которых больше симметрий.

Самыми совершенными из фигур считают круг и его пространственное порождение – шар, ведь круг и шар переходят сами в себя при любом повороте вокруг своего центра, при симметрии относительно любого своего диаметра, т.е. эти фигуры обладают бесконечным множеством симметрий.

По тому, сколько симметрий имеют фигуры, можно проводить их классификацию. Распределение по классам симметрий даёт нам новый взгляд на фигуры. Фигур любого класса можно придумать сколь угодно много. Итак мы в общих чертах рассмотрели принцип наведения порядка в множестве фигур. Но порядок – это и есть ГАРМОНИЯ.

Искусству конструирования можно научиться у природы- создательницы организмов, геометрическому изяществу которых позавидует любой математик. Посмотрим на простейшие морские организмы радиолярии, они совсем незаметны невооружённым глазом, но если посмотреть в микроскоп, то откроется фантастическая природная геометрия симметрий разного порядка.

Различные виды симметрии используются в декоративно прикладном искусстве. Разные виды симметрий мы встречаем в розетках. Розетки – это круглые орнаменты, встречающиеся в резьбе по дереву, в настенной лепке, в вышивках, в ковровых изделиях.

Основой розетки является круг, который разбивают на части, в одной из них рисуют орнамент и повторяют его во всех остальных частях.

Симметрия, воспринимаемая человеком как внешнее проявление внутреннего порядка, начинает обладать эстетической ценностью. Простой пример убеждает нас в этом. Чернильная клякса сама по себе некрасива. Но стоит свернуть лист бумаги с невысохшей кляксой пополам, и мы получаем уже кляксу, которая производит приятное впечатление. Различные виды симметрий, применённые к новой кляксе позволят создать затейливые узоры, которые нельзя назвать некрасивыми. Нам нравиться вглядываться в узоры симметрии, постигать их законы, и они воспринимаются нами как красивые.

Симметрия часто встречается в самых различных видах искусства. В музыке, ряд музыкальных форм строится симметрично. В этом отношении особенно характерно рондо, в котором музыкальная тема многократно повторяется, чередуясь с эпизодами различного содержания. Это напоминает зеркальную симметрию, где основная тема служит плоскостью, от которой отражаются эпизоды.

Искусство танца также не лишено симметрии. Танец любого ансамбля строится на построении симметричных танцевальных фигур. Балерина заканчивает свой номер искромётным фуэте, когда она вращается на одной ножке 12, 24, 32!раза. Именно повторяемость этих движений определяет их эстетический эффект.

Нагляднее всего симметрия видна в архитектуре. Достаточно вспомнить строго симметричные формы античных архитектурных памятников. Выбирая эти формы, художники тем самым выражали своё понимание природной гармонии, как устойчивости, спокойствия и равновесия. Храмы, посвящённые богам, должны были быть именно такими.

Симметрия обнаруживаемая в жизни, в искусстве, в технике является одним из принципов гармоничного построения мира. Но, как и в любом деле, абсолютизация одной идеи не приводит ни к чему хорошему. Сведение гармонии и красоты только к симметрии ограничивало богатство её внутреннего содержания. Истинную красоту можно постичь только в единстве противоположностей. Вот почему асимметрия стала завоёвывать себе место в жизни. Симметрия воспринимается нами, как покой, скованность, закономерность, тогда как асимметрия означает движение, свободу, случайность. Противопоставление симметричного и ассиметричного мы встречаем в науке. Известный микробиолог Луи Пастер считал, что именно асимметрия отличает живое от искусственно организованного неживого. Ему казалось, что стоит узнать способ, которым природа ввела асимметрию в органические соединения, - и до разгадки жизни – всего один шаг

Примером удивительного сочетания симметрии и асимметрии является Покровский собор на Красной площади в Москве. Эта причудливая композиция из десяти храмов, каждый из которых обладает центральной симметрией, в целом не имеет ни зеркальной, ни поворотной симметрии. Симметричные архитектурные детали собора кружатся в своём ассиметричном беспорядочном танце вокруг его центрального шатра. Без своей удивительной асимметрии Храм Василия Блаженного просто немыслим!

Итак, сфера влияния симметрии, а значит и её антипода асимметрии поистине безгранична. Всюду мы видим противоборство, а часто и единство двух великих начал симметрии и асимметрии, которые во многом и определяют гармонию природы, мудрость науки и красоту искусства.

Домашнее задание:

1. Придумать и нарисовать фигуры того же класса симметрий, что и класс симметрий а) правильного треугольника б) квадрата.

2. Темы докладов и сообщений

• Симметрия и асимметрия в декоративно- прикладном искусстве
  
• Симметрия и асимметрия в природе
  

Литература

1.А.И.Азевич «Двадцать уроков гармонии» библиотека журнала «Математика в школе», выпуск 7. Москва «Школа-Пресс», 1998год

2. А.В. Волошинов «Математика и искусство», Москва, «Просвещение»,

1992 ГОД

3. И.Ф.Шарыгин, Л.Н. Ерганжиева «Наглядная геометрия 5-6 классы» Москва, Издательский дом «Дрофа», 1998 год.

4. DVD Tsarskoe selo Master Video, 2004

5. CD Microsoft Office at school


Урок №3

Тема урока: Геометрия орнаментов, бордюров, паркетов.

Цель урока: рассмотреть геометрические подходы при конструировании орнаментов, бордюров, паркетов.


План проведения урока


Объяснение нового материала ведётся в форме беседы учителя с учащимися. Рассказ учителя сопровождается показом презентации «Геометрия орнаментов, бордюров, паркетов».

Тезисы к рассказу учителя.

Орнаментальное искусство одно из самых древних. С орнаментами мы встречаемся повсюду: в декоративно-прикладном искусстве, в росписях архитектурных сооружений, в чугунных решётках, окаймляющих сады, парки, дворцы. Орнамент – это узор, состоящий из повторяющихся, ритмически упорядоченных элементов. Орнамент, как правило, подчёркивает своим построением и формой архитектурные и конструктивные особенности предмета, природную красоту материала. В построении орнамента используют главным образом принцип симметрии.

Практическая работа. «СНЕЖИНКА» Взять квадратный лист бумаги (можно бумажную салфетку), вырезать из него круг, затем 4 раза свернуть пополам . В сложенной бумаге вырезать ножницами узор, так, чтобы были прорезаны все слои бумаги. Развернуть, получили орнамент «снежинку». Увеличивая количество осей симметрии можно получать новые и необычные «снежинки».

Каждая эпоха, каждая национальная культура разрабатывала свою систему орнаментов.

Древний Египет. В орнаментах этой эпохи чаще всего встречаются растительные мотивы, листья и цветы лотоса. Эти орнаменты таинственны и загадочны, при рассмотрении их с разных точек, они предстают перед нами совершенно в новом виде.

Древняя Греция. Самое большое распространение получили орнаменты, которые называются «меандр», и «акант». Слово «меандр» происходит от названия очень извилистой реки в Малой Азии. Орнамент «меандр» как будто повторяет излучины этой прихотливой реки. Акант - это травянистое растение распространённое в Средиземноморье, с большими листьями и изогнутыми стеблями.

Мусульманский Восток Орнаментальное искусство мусульманского Востока достигло высочайшего совершенства. Ковры и гобелены Востока неповторимы по своей красоте и оригинальности. Для этих орнаментов характерно сочетание только геометрических и растительных мотивов, так как Кораном запрещено изображать людей и животных. Впоследствии этот вид орнамента получил название «арабеска».

Средневековая Русь. Высокого уровня достигло искусство орнамента средневековой Руси. Для него характерны как геометрические и растительные мотивы, так и изображения зверей, птиц, фантастических животных, человеческих фигурок. Наиболее ярко эти орнаменты представлены в вышивках. Полотенца, скатерти, салфетки, праздничная одежда на Руси традиционно украшалась вышивкой. Большого мастерства достигли русские золотошвеи и вышивальщицы жемчугом. Праздничные церковное облачение, платья для коронации всегда традиционно украшались жемчужным шитьём. Орнаменты этих вышивок просты и совершенны в своей простоте. Резьба по дереву – один из традиционно русских видов прикладного искусства. Внутреннее убранство почти всех дворцов украшено золочённой резьбой по дереву, эти украшения представляют собой орнаменты, выполненные в виде изящных растительных побегов. Легкость и красота этих узоров поражают своим совершенством и строго симметрией рисунка. Искусство керамики – одно из древнейших достижений человеческой культуры. Достойное место в ней занимает искусство русского изразца. Мастера русского изразца создавали разнообразные композиции с растительно-геометрическим орнаментом, с птицами среди ветвей, используя при этом цветные эмали, и глазурь.

Орнаменты бывают ленточными (их называют бордюрами) и сетчатыми.

Бордюры.

Бордюром называют плоскую геометрическую фигуру, характеризующуюся векторами а и na (где n целое число), при которых эта фигура переходит в себя, но не переходит в себя при параллельных переносах другого вида. Вектор а называют направляющим для бордюра. Чтобы построить бордюр, достаточно нарисовать какую-нибудь геометрическую фигуру (фундаментальную область бордюра) и выполнить её параллельный перенос вправо и влево на заданный вектор. Доказано, что существует семь классов симметрий бордюров.

1. Бордюры, которые не имеют других симметрий, кроме параллельных переносов.
   
2. Бордюры, у которых фундаментальная область обладает центром симметрии.
   
3. Бордюры, у которых фундаментальная область имеет ось симметрии параллельную вектору а.
   
4. Бордюры, у которых фундаментальная область имеет ось симметрии перпендикулярную вектору а.
   
5. Бордюры, у которых фундаментальная область имеет ось симметрии перпендикулярную вектору а и ось симметрии параллельную вектору а.
   
6. Бордюры, имеющие такие оси симметрии, которых нет у фундаментальных областей.
   
7. Бордюры, имеющие такие оси симметрии, которых нет у фундаментальных областей.
   

Чугунное кружево Санкт-Петербурга

Кто бывал в Санкт-Петербурге, наверняка обратил внимание на удивительные чугунные решётки, окаймляющие сады, парки, дворцы, набережные города. Все вместе они образуют изумительное чугунное кружево, которым так знаменит Санкт-Петербург. Орнаменты каждой такой решётки уникальны и неповторимы. Мастера как будто соревнуются друг с другом в мастерстве и оригинальности композиции. Строгие геометрические формы переплетаясь с растительными композициями образуют причудливый орнамент. Замечательна решётка Летнего сада, поражающая благородством своих форм. Её строгий геометрический орнамент изящен и прост, здесь властвует симметрия, основоположница величия и покоя.

Помимо бордюров известен другой вид орнамента – сетчатый.

Он заполняет всю плоскую поверхность сплошным узором. Для построения такого орнамента выделяют плоскую решётку, фундаментальную ячейку; в ней выполняют рисунок, в котором одинаковые части повторяются в определённой геометрической последовательности; а потом с помощью параллельных переносов заполняют всю плоскость.

Различают пять типов плоских решёток, каждая из которых определяется двумя векторами a, b и углом между ними x⁰.

1. квадратная (а= b, x=90⁰)
   
2. прямоугольная (, x=90⁰)
   
3. гексанальная (а= b, x=60⁰)
   
4. ромбическая (а= b, x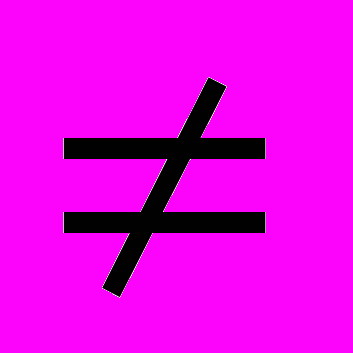90⁰, x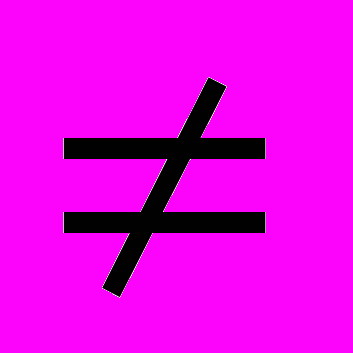60⁰)
   
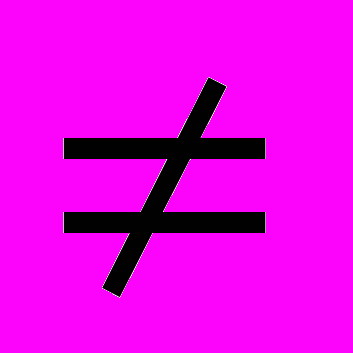5. косая (x90⁰ )
   

Зная эти геометрические закономерности можно и самим сконструировать интересный сетчатый орнамент.

Паркеты.

В математике паркетом называют замощение плоскости повторяющимися фигурами без пропусков и перекрытий. Установлено, что вокруг одной точки могут лежать либо шесть правильных треугольников, либо четыре квадрата, либо три правильных шестиугольника. Процесс «замощения» может быть продолжен дальше, таким образом можно получить простейшие паркеты.


Домашнее задание: 1. Составить эскиз более бордюра, у которого фундаментальная область обладает центром симметрии.

2. Составить сетчатый орнамент на основании квадратной решётки.


Литература:

1.А.И.Азевич «Двадцать уроков гармонии» библиотека журнала «Математика в школе», выпуск 7. Москва «Школа-Пресс», 1998год

2. А.В. Волошинов «Математика и искусство», Москва, «Просвещение»,

1992 год.

3. И.Ф.Шарыгин, Л.Н. Ерганжиева «Наглядная геометрия 5-6 классы» Москва, Издательский дом «Дрофа», 1998 год.

4. DVD Tsarskoe selo Master Video, 2004

5. CD Microsoft Office at school


Урок №4