Geum.ru

Элективный курс «Математика и гармония окружающего мира»

Вид материалаЭлективный курс

Содержание


Цель урока
Л. Кэррол
Домашнее задание.
Цель уроков
Подобный материал:
1   2   3   4
Тема урока: Пять красивых тел. Правильные многогранники.

Цель урока: Рассмотреть правильные многоугольники, их свойства и их место в гармонии мироздания.


План проведения урока.


Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук.

Л. Кэррол


Мир наш исполнен симметрии. С древнейших времен с ней связаны наши представления о красоте. Наверное, этим объясняется непреходящий интерес человека к правильным многогранникам - удивительным символам симметрии, привлекавшим внимание множества выдающихся мыслителей, от Платона и Евклида до Эйлера и Коши.

Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Многогранник называется правильным, если он лежит по одну сторону от плоскости любой его грани, т.е. является выпуклым, и все его грани есть равные правильные многоугольники.

Простой подсчет суммы углов при вершине правильного многогранника показывает, что существуют только пять правильных многогранников.

Форму правильных тел, по-видимому, подсказала древним грекам сама природа:

1) Кристаллы поваренной соли имеют форму куба;

2) Правильная форма алмаза – октаэдра;

3) Кристаллы пирита – додекаэдра.

Важным свойством правильных многогранников является существование для каждого из них вписанного и описанного шаров (сфер) таких, что поверхность вписанного шара касается центра каждой грани правильного многогранника, а поверхность описанного шара проходит через все его вершины. Центры этих шаров совпадают между собой и с центром соответствующего многогранника.

Концепция четырех элементов

С древнейших времен наши представления о красоте связаны с симметрией. Наверное, этим объясняется интерес человека к многогранникам - удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей. История правильных многогранников уходит в глубокую древность. Правильными многогранниками восхищались Пифагор и его ученики. Их поражала красота, совершенство, гармония этих фигур. Пифагорейцы считали правильные многогранники божественными фигурами и использовали в своих философских сочинениях

Ко времени Платона в античной философии созрела концепция четырех элементов(стихий) – первооснов материального мира: огня, воздуха, воды и земли.
  • Форма куба – атомы земли, т.к. и земля, и куб отличаются неподвижностью и устойчивостью.
  • Форма икосаэдра – атомы воды, т.к. вода отличается своей текучестью, а из всех правильных тел икосаэдр – наиболее «катящийся»
  • Форма октаэдра – атомы воздуха, ибо воздух движется взад и вперед и октаэдр как бы направлен одновременно в разные стороны
  • Форма тетраэдра – атомы огня, т.к. тетраэдр наиболее остр, кажется, что он мечется в разные стороны.
  • Платон вводит пятый элемент – «пятую сущность» - мировой эфир, атомам которого придается форма додекаэдра как наиболее близкому к шару.

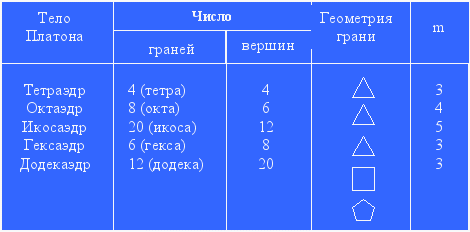
Математические свойства правильных многогранников

Формула Эйлера Г + В – Р = 2



Иоганн Кеплер

Иоганн Кеплер (1571-1630) – выдающийся немецкий математик, физик, астроном. Следуя пифагоро-платоновской традиции, Кеплер верил, что в основе миросоздания лежат простые числовые соотношения и совершенные геометрические формы.

Вселенная устроена на основе единого геометрического принципа (по И.Кеплеру).
  • В сферу орбиты Сатурна вписываем куб, в куб – сферу Юпитера.
  • В сферу Юпитера вписываем тетраэдр, в тетраэдр –сферу Марса.
  • В сферу Марса вписываем додекаэдр, в додекаэдр – сферу Земли.
  • В сферу Земли вписываем икосаэдр, в икосаэдр – сферу Венеры.
  • В сферу Венеры вписываем октаэдр, в октаэдр – сферу Меркурия..
  • В центр всей системы И.Кеплер поместил Солнце.

Математические расчёты показали, что совпадение с данными Коперника по радиусам планетных орбит было поразительным, но всё-таки не совсем точным. Однако, эта работа привела к открытию Кеплером истинных астрономических законов- трёх знаменитых законов Кеплера, на базе которых И.Ньютон построил свою теорию тяготения.

Идеи Пифагора, Платона, Кеплера нашли своё продолжение и в наши дни. Замечено, что наша матушка-Земля последовательно проходит эволюцию правильных объемных фигур. Существует много данных о сравнении структур и процессов Земли с вышеуказанными фигурами.

   Полагают, что четырем геологическим эрам Земли соответствуют четыре силовых каркаса правильных Платоновских тел: Протозоа - тетраэдр (четыре плиты) Палеозою - гексаэдр (шесть плит) Мезозою - октаэдр (восемь плит) Кайнозою - додекаэдр (двенадцать плит).

С позиций изучения симметрии, учитывая представление о додекаэдро-икосаэдрическом силовом каркасе Земли как планеты, следует признать, что в этом смысле Земля является живым существом. С душою, которую П.А. Флоренский назвал “пневматосфера”, со свободой воли и разумом.

Московские инженеры В.Макаров и В. Морозов высказали гипотезу, что ядро Земли имеет форму и свойства растущего кристалла, лучи или силовое поле кристалла обуславливают икосаэдро- додекэдровую структуру Земли. Она проявляется в том, что в земной коре как бы проступают контуры вписанных икосаэдра и додекаэдра. Многие залежи полезных ископаемых тянутся вдоль этой сетки, а в узлах располагаются очаги древнейших культур и цивилизаций. В этих точках расположены загадки Земли: озеро Лох-Несс, Бермудский треугольник. Дальнейшие исследования Земли определят отношение к этой гипотезе, в которой правильные многогранники занимают важное место.

Полуправильные многогранники (тела Архимеда)

Звёздчатые многогранники (тела Кеплера - Пуансо)


Домашнее задание.

Изготовить модели пяти правильных многогранников с ребром равным 5 см.


Литература:

1.А.И.Азевич «Двадцать уроков гармонии» библиотека журнала «Математика в школе», выпуск 7. Москва «Школа-Пресс», 1998год

2. А.В. Волошинов «Математика и искусство», Москва, «Просвещение»,

1992 ГОД

3. Энциклопедический словарь юного математика Москва 1989 год.


Урок №15

Тема урока: Итоговое тестирование по всему курсу.

Цель урока: контроль знаний учащихся.


План проведения урока.

  1. Фронтальный обзор изученных тем.
  2. Контроль знаний учащихся

Контроль будет осуществляться в виде теста с выбором правильного ответа. Создана компьютерная версия этого теста с помощью программы Tester, созданной учителями и учащимися лицея. Тест содержит 25 вопросов по всем рассматриваемым темам. Таким образом, тестирование будет проводиться на компьютере с последующей оценкой и анализом знаний учащихся.

Вопросы теста
  1. Главный храм на Афинском Акрополе?
  • Пантеон
  • Парфенон
  • Храм Артемиды
  1. Одна из известнейших скульптур Древней Греции, канон пропорций человеческого тела?
    • Дорифор
    • Август
    • Марк Аврелий
  2. Что такое «Золотое сечение»?
  • Часть площади геометрической фигуры
  • Точка пересечения двух прямых
  • Соотношение двух отрезков, имеющее постоянную величину
  1. Наличие какого геометрического свойства в объекте придаёт ему устойчивость, прочность, надёжность?
  • Асимметрия
  • Симметрия
  • Внушительные проблемы
  1. Какие из следующих преобразований относятся к нетрадиционным видам симметрии?
  • осевая симметрия
  • зеркальная симметрия
  • винтовая симметрия
  1. Какая из геометрических фигур обладает наибольшим количеством симметрий?
  • Круг
  • Квадрат
  • Правильный треугольник
  1. Асимметрия в природе означает…
  • покой, скованность, закономерность
  • движение, свобода, случайность
  • хаос, неразбериха, неустойчивость
  1. В орнаментах Древнего Египта чаще всего встречаются …
  • Ветви пальмы
  • Фигурки зверй и птиц
  • Цветы и листья лотоса.
  1. Стиль Древнегреческих орнаментов МЕАНДР означает…
  • контуры цветка
  • путь в лабиринте
  • название извилистой реки
  1. Почему в орнаментах стран мусульманского Востока присутствуют только геометрические и растительные элементы?
  • листья растений более всего украшают орнамент
  • изображать фигурки людей и животных запрещает Коран
  • изображение фигурок людей и животных – трудоёмкая работа
  1. Какая из трёх проекций сохраняет все свойства оригинала?
  • Центральная проекция
  • параллельная проекция
  • ортогональная проекция



  1. Кто впервые высказал мысль о том, что для точного определения точки в пространстве по её чертежу, необходимо иметь две проекции этой очки, полученные при двух направлениях проектирования?
  • Рене Декарт
  • Гаспар Монж
  • Карл Гаусс
  1. Перспектива – это…
  • ортогональная проекция
  • аксонометрическая проекция
  • центральная проекция



  1. Искусству какой эпохи более всего свойственно ортогональное проектирование?
  • Древний Египет
  • Древняя Греция
  • Древний Рим
  1. Какой способ отображения пространства на плоскость использовали живописцы эпохи Возрождения?
  • линейную перспективу
  • параллельную проекцию
  • ортогональную проекцию



  1. В живописных полотнах каких мастеров мы сталкиваемся с идеями обратной перспективы?
  • Леонардо да Винчи
  • Рафаэль Санти
  • Андрей Рублёв
  1. Число Фидия равно…
  • 0,3141
  • 0.6183
  • 0.7232
  1. Стороны пентаграммы пересекаясь делят друг друга на отрезки, длины которых образуют…
  • арифметическую прогрессию
  • золотую пропорцию
  • геометрическую прогрессию
  1. Кто из древних зодчих стремился установить законы пропорциональности человеческого тела и воплотил их в скульптуре «Дорифор»?
  • Фидий
  • Поликлет
  • Мтикеланджело
  1. Кто впервые сформулировал закон архитектурного целого?
  • Ле Корбюзье
  • Зодчий Хесира
  • М.Витрувий
  1. Какое архитектурное сооружение считается самым ярким примером использования «золотой пропорции»?
  • Парфенон
  • Пирамида Хеопса
  • Собор Василия Блаженного
  1. Кто из великих математиков древности считал, что число правит миром?
  • Платон
  • Аристотель
  • Пифагор
  1. Сколько существует правильных многогранников?
  • 4
  • 5
  • 6



  1. Сколько граней у додекаэдра?
  • 12
  • 13
  • 14
  1. Кто из учёных открыл три основных астрономических закона?
  • Ньютон
  • Коперник
  • Кеплер.



  1. Предложить учащимся темы для создания совместного проекта на двух последующих уроках.
    • Симметрия правильных многоугольников.
    • Построение розеток и задачи деления окружности на части.
    • Перспектива и законы зрительного восприятия.
    • Обратная перспектива древнерусских икон.
    • Молекулярные тайны жизни и золотое сечение.
    • Ритмы стихосложения и золотое сечение.
    • Геометрия архитектурных стилей.
    • Архитектура, бионика, геометрия.
    • Замечательные кривые в живой природе.
    • Математические основы восприятия прекрасного.
  2. Домашнее задание

Продумать план работы над проектом по выбранной теме.


Уроки №16-17

Тема уроков: Создание проекта « Математика и гармония окружающего мира»

Цель уроков: создать групповой проект по дополнительным вопросам изученной темы.


План проведения уроков.


На предыдущем уроке учащимся были предложены на выбор 10 дополнительных тем для создания совместного проекта.

    • Симметрия правильных многоугольников.
    • Построение розеток и задачи деления окружности на части.
    • Перспектива и законы зрительного восприятия.
    • Обратная перспектива древнерусских икон.
    • Молекулярные тайны жизни и золотое сечение.
    • Ритмы стихосложения и золотое сечение.
    • Геометрия архитектурных стилей.
    • Архитектура, бионика, геометрия.
    • Замечательные кривые в живой природе.
    • Математические основы восприятия прекрасного.


На двух уроках учащимся предлагается поработать над выбранной темой, подобрать материал, используя возможности сети Интернет, и создать презентацию.

Все презентации собрать в единое целое. Весь проект рассмотреть на последнем уроке с защитой своего блока каждым учащимся.