Элективный курс «Математика и гармония окружающего мира»
| Вид материала | Элективный курс |
- Липецка Учитель Тарасова Светлана Васильевна. Предмет математика. Класс 9 элективный, 242.74kb.
- Элективный курс 11 класс «методы научного познания и физическая картина мира» (авторская, 107.2kb.
- Элективный курс «Уравнения и неравенства с модулем» 10 класс разработан учителем моу, 93.7kb.
- Элективный курс "Музыка мира: джаз" Пояснительная записка Элективный курс "Музыка мира:, 177.75kb.
- Элективный курс " Лексика и фразеология" Пояснительная записка, 71.55kb.
- Конспект урока окружающего мира в 3 классе умк «Гармония», 90.12kb.
- Кирилина Лидия Ивановна 2008 Содержание Введение 3 История математики на урок, 220.88kb.
- Элективный курс «глобальные проблемы человечества», 121.74kb.
- В. А. Ходаков моу воротынская средняя школа Перемышльского района Калужской области, 76.7kb.
- Элективный курс по астрономии, 93.86kb.
Цель урока: Познакомиться с проявлением закона золотого сечения в архитектуре.
План проведения урока.
Урок проходит в форме беседы с учащимися. На протяжении всего урока идёт обращение к презентации «Геометрия архитектурной гармонии»
- Язык пропорций – язык архитекторов. (слайд 1-3)
Пропорциональность является наиболее ярким, зримым, объективным и математически закономерным выражением архитектурной гармонии. Пропорция – это математическая закономерность, прошедшая через душу зодчего. Это поэзия числа и геометрии на архитектурном языке. На языке пропорций говорили зодчие всех времён и архитектурных направлений: древние египтяне и греки, средневековые каменотёсы и древнерусские плотники, представители барокко и классицизма, конструктивисты и модернисты.
Архитектура триедина: она извечно сочетает в себе логику учёного, ремесло мастера и вдохновение художника. «Прочность- польза - красота»- такова знаменитая формула единого архитектурного целого, выведенная древнеримским теоретиком зодчества Марко Витрувием. Люди всегда стремились достичь гармонии в архитектуре. Благодаря этому стремлению на свет появлялись всё новые изобретения, конструкции и стили.
Для достижения гармонии в произведениях искусства должен выполняться принцип Гераклита: «из всего – единое, из единого - всё». Гармония в архитектурном сооружении зависит не столько от его размеров, сколько от соотношений между размерами составляющих его частей.
Гармония в природе и гармония в архитектуре обретают одинаковое математическое выражение в законе золотого сечения.
- Древнеегипетские пирамиды. (слайды 4-5)
Конструкция древнеегипетской пирамиды является самой простой, прочной и устойчивой, её масса уменьшается по мере увеличения высоты над землёй. Форма пирамиды, подчёркнутая её огромными размерами, придают ей особую красоту и величие, вызывает ощущение вечности, бессмертия, мудрости и покоя.
- Тайны древних пропорций. Парфенон (Слайды 6-8)
Многие исследователи, стремившиеся раскрыть секрет гармонии Парфенона, искали и находили в соотношениях его частей золотое сечение. Если принять за единицу ширины торцовый фасад храма, то получим прогрессию, состоящую из восьми членов ряда: 1 : j : j 2 : j 3 : j 4 : j 5 : j 6 : j 7, где j =1,618
Парфенон является самым ярким примером использования золотой пропорции в архитектуре.
Парфенон был и остаётся совершеннийшим из архитектурных сооружений, архитектурной скульптурой, мраморным сводом законов античного зодчества.
- Собор Нотр-Дам де Пари (слайды 9-10)
Собор Парижской Богоматери- самый величественный памятник ранней готики. В гордой размеренности западного фасада собора горизонтальные линии ещё соперничают с вертикальными. Ещё не исчезла стена фасада, но она уже приобрела лёгкость и даже прозрачность. Пропорциональную основу западного фасада собора Нотр – Дам составляет квадрат, а высота башен фасада равна половине стороны этого квадрата…
- Церковь Покрова Богородицы на Нерли (слайды 11-12)
Крестово-купольная схема лежит в основе храма Покрова на Нерли. Для него характерно спокойное равновесие, основанное на симметрии. Храм кажется удивительно лёгким, устремлённым ввысь. В основе архитектурного плана церкви лежит прямоугольник со сторонами 1 и √2 и диагональю √5, в этих числах легко угадываются все составляющие, с помощью которых выражается золотая пропорция.
- Церковь Вознесения в Коломенском (слайд 13)
Храм Вознесения является не только гимном расправляющей крылья России, но и архитектурным гимном геометрии
- Геометрия куполов- геометрия горящей свечи (слайд 14)
В русском церковном искусстве проявилось стремление эстетику чувств сочетать с эстетикой чисел, красоту свободно льющегося ритма с красотой правильного геометрического тела. М.В.Алпатов
- Храм Василия Блаженного (слайды 15-16)
Трудно найти человека, который бы не знал собора Василия Блаженного на Красной площади. Храм этот особенный, он отличается удивительным разнообразием форм и деталей, красочных покрытий, ему нет равных в нашей стране. Архитектурное убранство всего собора продиктовано определенной логикой и последовательностью развития форм. Исследуя храм, пришли к выводу о преобладании в нем ряда золотого сечения. Если принять высоту собора за единицу, то основные пропорции, определяющие членение целого на части, образуют ряд золотого сечения:
1 : j : j 2 : j 3 : j 4 : j 5 : j 6 : j 7, где j =0,618
9. Модулор Ле Корбюзье (слайды 17-18)
Идея построения модулора гениально проста. Модулор – это ряд золотого сечения. «Модулор – это гамма пропорций, которая делает плохое трудным, а хорошее - лёгким» А. Энштейн
«Модулор это гамма. Музыкант располагает гаммой и создаёт музыку по своим способностям – банальную или прекрасную» Ле Корбюзье
Лучезарный дом в Марселе - воплощение здравого смысла, ясного, прямолинейного и рационального. Капелла в Роншане представляет собой нечто иррациональное, пластическое, скульптурное, сказочное. Единственное, что объединяет эти два памятника зодчества – это модулор, архитектурная гамма пропорций общая для обоих произведений.
- Заключение.(слайд 19) Что объединяет все системы пропорциональности?
Любая пропорциональная система – это основа, скелет архитектурного сооружения, это та гамма, а точнее тот лад, в котором будет звучать архитектурная музыка.
- Домашнее задание:
Темы докладов и сообщений.
- Пропорции и меры в архитектуре Древней Руси.
- Пропорции современных архитектурных ансамблей России.
Литература:
1.А.И.Азевич «Двадцать уроков гармонии» библиотека журнала «Математика в школе», выпуск 7. Москва «Школа-Пресс», 1998год
2. А.В. Волошинов «Математика и искусство», Москва, «Просвещение»,
1992 ГОД
3. Энциклопедический словарь юного математика Москва 1989 год.
4. И.Ф.Шарыгин, Л.Н. Ерганжиева «Наглядная геометрия 5-6 классы» Москва, Издательский дом «Дрофа», 1998 год.
5. DVD Tsarskoe selo Master Video, 2004
6. CD Microsoft Office at school
Урок № 12
Тема урока: Пифагор и пифагорейское учение о числе.
Цель урока: познакомить учащихся с биографией, философскими взглядами и научными открытиями Пифагора и пифагорейской школы.
План проведения урока.
"ЧИСЛО ЕСТЬ СУЩНОСТЬ ВСЕХ ВЕЩЕЙ"
Урок - лекция. Сопровождается демонстрацией презентации.
Тезисы лекции.
Пифагор известен школьникам главным образом по геометрической теореме о связи между сторонами прямоугольного треугольника. Для современников этот греческий мудрец уже казался полубогом. Его религиозно-философское учение и основанный им союз пифагорейцев оказали большое влияние на жизнь Греции и позднее на развитие философии в средневековье и даже в новом времени. В математике с его именем также связаны и другие открытия.
ПИФАГОР Самосский (6 в. до н. э.), древнегреческий философ, религиозный и политический деятель, основатель пифагореизма, математик. Его биография стала легендой. А самого Пифагора называли на одну десятую гением, на девять десятых выдумкой. По преданию вид его был так величествен, что ученикам часто казалось, будто сам бог Аполлон говорит с ними.
Родился Пифагор на острове Самос, расположенном в Эгейском море у берегов Малой Азии, около 570 года до н.э. Отец Пифагора Мнесарх был резчиком по драгоценным камням. Юношей Пифагор отправился в путешествие по странам Востока, посетил Египет, бывал в Вавилоне и во многом воспринял восточную мудрость. Вернувшись на родину, Пифагор собирает вокруг себя единомышленников. Однако скоро покидает родной город и поселяется в в Кротоне. «Здесь он приобрёл всеобщее уважение как человек , много странствующий, многоопытный и дивно одарённый судьбою и природою: с виду он был величав и благороден, а красота и обаяние были у него и в голосе, и в обхождении, и во всём…»
Пифагор – олимпийский чемпион по кулачному бою
В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена, члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Система жизненных принципов и правил, проповедуемая Пифагором, и сейчас достойна подражания.
Золотые стихи Пифагора. (см дополнительный материал)
Ритуал посвящения в члены пифагорейского братства был окружён множеством таинств, разглашение которых сурово каралось. Главным пифагорейским символом была пентаграмма – звёздчатый пятиугольник, она содержит в себе все пропорции известные пифагорейцам, видимо именно поэтому была выбрана в качестве их опознавательного символа .
Что отличало пифагорейцев от всех других сект так это то, что математика была одной из составных частей их религии. Именно в математике, в познании количественных отношений, видели пифагорейцы ключ к разгадке мировой гармонии, постижение которой и составляло смысл их жизни.
Пифагорейцам удалось сформулировать два тезиса, значимость которых подтвердило всё последующее развитие науки:
- во- первых, что основополагающие принципы, на которых зиждется мироздание, можно выразить на языке математики;
- во –вторых, что объединяющим началом всех вещей служат числовые отношения, которые выражают гармонию и порядок природы.
Однако, в первоначальном виде пифагорейский союз просуществовал недолго и около 510 года до н.э. подвергся кровавой расправе. Пифагорейцы бежали из Кротона в другие города, что во многом способствовало распространению учения Пифагора по всей Греции и даже за её пределами. Сам Пифагор удалился в город Метапонт, расположенный неподалёку от Кротона, где и провёл остаток своей жизни.
ПИФАГОРЕИЗМ, религиозно-философское учение до н. э., основанное Пифагором и исходившее из представления о числе как основе всего существующего. Числовые соотношения — источник гармонии космоса, структура которого мыслилась в пифагореизме как физико - геометрическо - акустическое единство. Пифагореизм внес значительный вклад в развитие математики, астрономии (утверждение о шарообразности Земли) и акустики.
Подлинно новым и революционным в пифагорейской научной системе явилось учение о числе. В числовых отношениях видели пифагорейцы ключ к разгадке всех тайн природы. Конечно же пифагорейцам была свойственна идеалистическая мистификация чисел. Но за этой формрй нельзя не видеть рационального содержания, которое всё яснее проступает на современном уровне развития научного познания.
Гёте удалось стряхнуть идеалистическую пыль с пифагорейской мудрости: «Числа не управляют миром, но показывают как управляется мир».
Однако сокрушительный удар по всей пифагорейской системе, пифагорейцы – истинные рыцари науки, вынуждены были нанести себе сами. Именно они обнаружили, что среднее геометрическое чисел 1 и 2 , другими словами √2, не выражается в виде отношения натуральных чисел. Говоря языком геометрии сторона квадрата несоизмерима с его диагональю. Это открытие долго держалось в тайне. Между тем именно это неосознанное открытие иррациональных чисел является наивысшим достижением пифагорейской школы. Ему было суждено пережить тысячелетия и стать поворотным этапом в развитии математики.
Домашнее задание:
Отыскать различные доказательства теоремы Пифагора.
Дополнительный материал
«ЗОЛОТЫЕ СТИХИ» ПИФАГОРА
ПРИГОТОВЛЕНИЕ
Должен бессмертным богам приносить ты законченную жертву;
Веру свою сохранять; чтить память великих героев;
Духам земным воздавать обычное им поклоненье
ОЧИЩЕНИЕ
Если в твоей это власти, ибо закон непреложный
Тесно связует возможность с необходимостью вместе.
Страсти свои побороть свыше дана тебе сила,
Так обуздай же в себе мощным усилием воли
Алчную жадность, и лень, похоть и гнев безрассудный.
Равно один и при людях, бойся дурного поступка;
Больше всего же стыдиться должен ты сам пред собою.
Будь справедлив и в словах, и в поступках своих неизменно,
Следуя в них непреклонно веленьям ума и закона;
Помни, что рок неизбежный к смерти людей всех приводит,
Помни, что блага земные, как с легкостью людям даются,
Так же легко исчезают. Что же касается горя,
Данного людям Судьбою, — то должен его ты с терпеньем
Кротким сносить, но при этом сколько возможно стараться
Горечь его облегчать: ибо бессмертные боги
Мудрых людей не повергнут свыше их силы страданью.
Много путей существует для хода людских рассуждений;
Много меж ними дурных, много и добрых, но прежде
Нужно в них зорко вглядеться, чтоб выбрать из них настоящий.
Если же в мире возьмет верх заблужденье над правдой,
Мудрый отходит и ждет воцарения истины снова.
Слушай внимательно то, что тебе я скажу, и запомни:
Да не смущают тебя поступки и мысли чужие;
Да не побудят тебя к вредным словам и деяньям.
Слушай советы людей, сам размышляй неустанно,
Ибо безумный лишь может действовать без рассужденья;
Делай лишь то, что потом в горе тебя не повергнет
И не послужит тебе причиной раскаянья злого.
За неизвестное дело ты не дерзай приниматься,
Но научися ему; этим ты счастья достигнешь.
Но изнурять ты не должен тело свое, а стараться
Пищи, питья, упражнений в меру давать ему, дабы
Тело твое укрепилось, не зная излишеств и лени.
В жизни своей соблюдай, сколько возможно, порядок,
Роскошь во всем изгони, ибо она возбуждает
Зависть людей неизбежно. Бойся скупым быть излишне,
Бойся добро расточать, как те, что не знают работы;
Делай лишь то, что тебя ни теперь, ни потом не погубит
И потому обсуждай каждый свой шаг и поступок.
СОВЕРШЕНСТВОВАНИЕ
Да не сомкнет тихий сон твои отягченные вежды,
Раньше чем трижды не вспомнишь дневные свои ты поступки.
Как беспристрастный судья их разбери, вопрошая:
«Доброго что совершил я? Из должного что не исполнил?»
Так проверяй по порядку все, что с утра и до ночи
Сделал ты в день — и за все, что содеяно было дурного,
Строго себя обличай, веселясь на добро и удачу.
Пользуйся сим наставленьем; думай над ним непрестанно
И постарайся к нему навсегда привязаться всем сердцем,
Ибо советы мои тебя к совершенству приблизят.
В этом клянусь тебе Тем, Кто вложил в нашу душу Тетраду,
Символ божественной сущности и добродетели высшей;
Но принимаясь за дело, прежде к богам обратися
С жаркой молитвой, дабы с помощью их ты окончил
Дело свое; а когда на пути ты своем укрепишься,
Все о бессмертных богах ты узнаешь, а также о людях,
О разделеньи существ; о Том, Кто в Себе их содержит,
Цепью единой скрепляя, а также о том, что Природа
Мира сего однородна и в Вечном мертвого нет вещества.
Это познав, ты надеждой тщетной себя не обманешь, -
Все тебе будет открыто.
Будешь ты знать еще то, что люди свои все несчастья
Сами своею виной на себя навлекают в безумьи
И выбирают свободно каждый свои испытанья.
Горе несчастным! В своем ослепленьи безумном не видят
Люди, что в их глубине таится желанное счастье.
Очень немного меж нами тех, что усилием могут
Сбросить несчастье с себя, ибо их Рок ослепляет:
Словно колеса они катятся с гор, за собою
Горестей бремя влача и раздоров, что с ними родятся,
Их управляя судьбой незаметно до самой кончины.
Вместо того, чтоб искать ссоры, где только возможно,
Люди должны бы ее избегать, уступая без спора.
Отче Зевес всемогущий! Ты один в силах избавить
Род весь людской от несчастья, Демона им показавши,
Что ослепляет их очи. Все же не должен надежду
Ты покидать на спасенье, ибо божественен корень
Рода людского и тайны Природа ему открывает.
Если же в них ты проникнешь, то скоро окончить ты сможешь
То, что тебе предписал я. Так излечив свою душу,
Будешь вполне ты свободен от этих работ над собою.
Но воздержися от мяса, оно помешает природе
При очищеньи твоем. Если же хочешь избавить
Душу свою от земного, то руководствуйся свыше
Данным тебе пониманьем. Пусть оно правит судьбою!
После того как очистишь душу свою совершенно,
Станешь ты богом бессмертным, смерть раздавившим стопою.
Литература:
1.А.И.Азевич «Двадцать уроков гармонии» библиотека журнала «Математика в школе», выпуск 7. Москва «Школа-Пресс», 1998год
2. А.В. Волошинов «Математика и искусство», Москва, «Просвещение»,
1992 ГОД
3. Энциклопедический словарь юного математика Москва 1989 год.
4. А.В. Волошинов «Пифагор» Москва 1992 год
Урок №13
Тема урока: Музыкальная гармония пропорций
Цель урока: Рассмотреть связь между законами математики и их проявлением в музыке.
План проведения урока
Урок проходит в виде беседы с учащимися при постоянном обращении к презентации.
Тезисы сообщения учителя
Музыка - это радость души,
которая вычисляет, сама того не замечая.
Г. Лейбниц
Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришёл к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и что между ними размещается всё, что человечество создало в области науки и искусства.
Генрих Нейгауз
Математика и музыка - два полюса человеческой культуры. Слушая музыку, мы попадаем в волшебный мир звуков. Решая задачи, погружаемся в строгое пространство чисел. И не задумываемся о том, что мир звуков и пространство чисел издавна соседствуют друг с другом.
«Музыка – величайшая сила. Она может заставить человека любить и ненавидеть, прощать и убивать».
Известно открытие Пифагора в области теории музыки. Необычность его в том, что сочетание звуков, издаваемых струнами, наиболее благозвучно, если длины струн музыкального инструмента находятся в правильном численном отношении друг к другу.
Для воплощения своего открытия Пифагор использовал монохорд - полуинструмент, полуприбор. Под струной на верхней крышке ученый начертил шкалу, с помощью которой можно было делить струну на части. Было проделано много опытов, в результате которых Пифагор описал математически звучание натянутой струны.
Архит родился в г. Таренте, был учеником пифагорейца Филолая, который сумел внушить ему интерес к научным проблемам своей школы. Судьба Архита сложилась счастливо: он семь раз избирался стратегом, при этом, как полководец, не проиграл ни одного сражения. Но самое главное он был разносторонним учёным, механиком, математиком. Он много занимался арифметикой натуральных чисел, далеко продвинул теорию несоизмеримых величин. Архит считается самым крупным теоретиком музыки античности.
В основе музыкальной системы были два закона, которые носят имена двух великих ученых - Пифагора и Архита.
1.Частота колебания f звучащей струны обратно пропорциональна ее длине l. f= a / l, (а - коэффициент, характеризующий физические свойства струны).
2. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т.е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n/(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
Эти интервалы – «совершенные консонансы», и их интервальные коэффициенты получили названия:
Октава l2/l1 =1/2 Квинта l2/l1 =2/3 Кварта l2/l1 =3/4
Основой музыкальной шкалы - гаммы пифагорейцев был интервал - октава. Она является консонансом, повторяющим верхний звук. Для построения музыкальной гаммы пифагорейцам требовалось разделить октаву на красиво звучащие части. Так как они верили в совершенные пропорции, то связали устройство гаммы со средними величинами: арифметическим, геометрическим, гармоническим.
Деление струны монохорда на части, образующие с ней совершенные консонансы
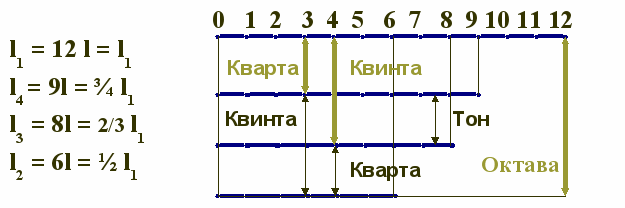
Квинта есть среднее гармоническое длин струн основного тона l1 и октавы l2
l3 =2l1l2/(l1+l2)
Октава есть произведение квинты на кварту или
l2/l3 = l4/l1
Кварта есть среднее арифметическое длин струн основного тона l1 и октавы l2
l4 = (l1+l2)/2
Построение пифагорейской музыкальной гаммы
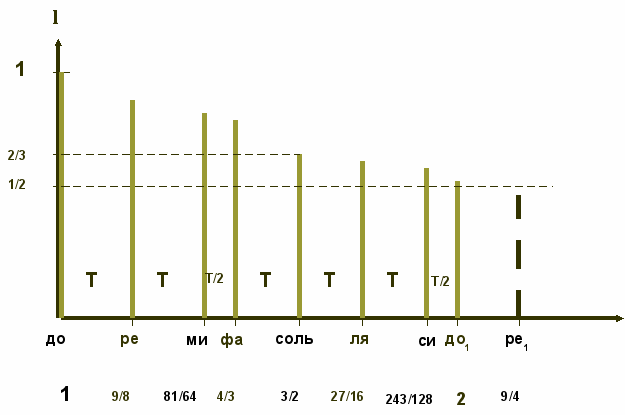
Построение музыкальной гаммы обладает такой особенностью: двигаясь по квинтам вверх и вниз, не получится точного октавного повторения исходного звука. Лишь 12 квинт приближенно равны 7 октавам, а разделяющий их интервал называется пифагоровой коммой. Несмотря на свою малость, пифагорова комма на протяжении столетий "резала ухо" музыкантам. Взяв отношение (3/2)12:27, можно найти численное значение пифагоровой коммы (1,0136).
На протяжении многих столетий музыканты настраивали инструменты так, как это делали в Древней Греции. Однако этот настрой не мог казаться им полностью подходящим, поскольку в нём сохранилась «пифагорова комма». Она была следствием несовершенства не только пифагорейской музыкальной гаммы, но и учения о числе. Теорию музыки оказалось возможным улучшить только после достаточного развития математики иррациональных величин.
Но прежде, чем в науке утвердилось новое учение о числе , прежде, чем появился новый музыкальный строй, прошла целая эпоха.
МУЗЫКАЛЬНЫЙ СТРОЙ, система отношений звуков по высоте. Тот или иной музыкальный строй характеризуется рядом чисел, каждое из которых показывает отношение частот колебаний верхних и нижних звуков интервала. Для одноголосной музыки ряда европейских народов типичен Пифагоров строй, в котором в качестве основы используется чистая квинта с отношением частот 3:2. Примерно с 16 в. в многоголосной музыке распространился т. н. чистый строй. В нем, кроме квинты, основанием служит большая терция (5:4). К началу 18 века утвердился равномерно-темперированный строй, в котором чистая октава (2:1) поделена на 12 равных полутонов ( Темперация).
Простой математический анализ многих музыкальных шедевров позволяет совершенно иными глазами взглянуть на них, увидеть их скрытую внутреннюю математическую красоту, которую мы только ощущаем, слушая произведение.
«При взгляде на математические схемы музыкальных произведений… невольно приходишь в священный трепет перед гениальностью мастера, воплотившего силой художественной чуткости до такой степени точности законы природного творчества» Розенов
Хроматическая фантазия Баха
Мы находим в произведениях Баха детальную и органическую сплочённость. Закон золотого деления проявляется в них с поразительной точностью в соотношениях крупных и мелких частей, как в строгих, так и в свободных формах, что, несомненно, соответствует характеру этого гениального композитора.
Лунная соната Бетховена
В «Лунной сонате» проявление закона золотого сечения глубоко логично, оно указывает на силу темперамента Бетховена и в точности совпадает со всеми моментами высшего напряжения чувств.
Увертюра к опере «Руслан и Людмила» Глинки
Простейший математический анализ музыкальных произведений М.И. Глинки убеждает в применении закона золотого сечения только лишь в широких масштабах при полном отсутствии мелочных соответствий.
Итак, гармония космоса была воплощена пифагорейцами в сфере музыки. Идея совершенства окружающего мира владела умами ученых и в последующие эпохи. В первой половине XVII в. И.Кеплер установил семь основных гармонических интервалов: октаву - 2/1, большую сексту - 5/3, малую сексту - 8/5, чистую квинту - 3/2, чистую кварту - 4/3, большую терцию - 5/4 и малую терцию - 6/5. С помощью этих интервалов он выводит весь звукоряд как мажорного, так и минорного наклонения. После долгих поисков гармоничных отношений "на небе", проделав огромную вычислительную работу, И.Кеплер установил, что отношения экстремальных углов скоростей для некоторых планет близки к гармоническим: Марс - 3/2, Юпитер - 6/5, Сатурн - 5/4.
До сих пор никому не удавалось найти алгоритм, порождающий простую и красивую мелодию. Мы просто не знаем, какое волшебство происходит в голове композитора, создающего неповторимую мелодию. Гениальное произведение - это результат вдохновения и мастерства его создателя. А еще своеобразная тайна, постичь которую порой невозможно. Решая задачи и слушая великую музыку, мы открываем в ней совершенство, простоту, гармонию и еще нечто такое, что неподвластно выражению словом...
Домашнее задание:
Подготовить сообщение с презентацией по теме: «Что общего между Пифагором и Бахом?»
Литература:
1.А.И.Азевич «Двадцать уроков гармонии» библиотека журнала «Математика в школе», выпуск 7. Москва «Школа-Пресс», 1998год
2. А.В. Волошинов «Математика и искусство», Москва, «Просвещение»,
1992 ГОД
3. Энциклопедический словарь юного математика Москва 1989 год.
4. И.Ф.Шарыгин, Л.Н. Ерганжиева «Наглядная геометрия 5-6 классы» Москва, Издательский дом «Дрофа», 1998 год.
5. DVD Tsarskoe selo Master Video, 2004
6. CD Microsoft Office at school
Урок №14
