Учебная рабочая программа элективного курса для учащихся 6 класса. Составитель: Сарычева Зоя Николаевна, учитель математики
| Вид материала | Рабочая программа |
- Учебная рабочая программа элективного курса для учащихся 9 класса. Составитель, 112.28kb.
- Программа элективного курса для обучающихся 9 класса основной школы Тип элективного, 53.13kb.
- Муравьева Инна Николаевна Р. п. Дмитриевка-2007 программа курса, 146.99kb.
- Учебная рабочая программа элективного курса для учащихся 5 класса. Составитель, 245.19kb.
- Программа составлена на основе программы элективного курса для учащихся 9-х классов, 200.18kb.
- Рабочая программа Учебного курса литература 5 класса Составитель, 551.62kb.
- Рабочая программа Учебного курса литература 6 класса Составитель, 355.66kb.
- Рабочая программа Учебного курса литература 5 класса Составитель, 563.19kb.
- Методическое пособие для учителя к программе элективного курса для обучающихся 9 класса, 459.09kb.
- Программа курса по выбору для учащихся 12 класса общеобразовательных учреждений, 93.91kb.
1) 12; 2) 24; 3) не знаю.
Б) золотая и серебряная медали.
1) 24; 2) 132; 3) 11.
( 12 · 11= 132)
В) золотая , серебряная, бронзовая медали.
1) 10; 2) не знаю; 3) 1320.
( 12 · 11 · 10 = 1320)
2) Сколько существует четырёхзначных чисел, в записи которых:
А) не повторяется ни одна из цифр
1) 4536; 2) 81; 3) 648.
( 9 · 9 · 8 · 7 = 4536)
Б) цифры могут повторяться
1) 900; 2) 9000; 3) не знаю.
(9 · 10 · 10 · 10= 9000 )
В) все цифры нечётные.
1) 25; 2) 625; 3) 125.
( 5 · 5 · 5 · 5= 625)
Г) все цифры чётные.
1) 8; 2) 20; 3) 500.
( 4 · 5 · 5 · 5= 500)
Код верных ответов 1, 2, 3, 1, 2, 3
II. Итог урока.
1) Что вызывает затруднения ?
2) Решит задачи ( по желанию)
№ 160, № 194, № 915.
Занятие № 6.
Тема « Принцип Дирихле»
Цель: познакомить учащихся с принципом Дирихле, учить применять его при
решении задач, рассуждать и устанавливать соответствие между данными
числами задачи.
План.
I. Повторение ранее пройденного материала.
1) Проверить решение домашних номеров, если кто-то сделал или разобрать их решение. ( № 160, № 194, № 915)
2) № 355 из « М-6»
3) № 53 из « М-6»
Работа группами.
II. Изучение нового материала.
1) Рассмотрим задачи:
А) Если 101 кролика рассадить в 100 клеток, то по крайней мере в одной клетке будет 2 кролика. Верно ли это ?
Б) А если бы было 35 клеток и 743 кролика, то что можно было бы утверждать ?
( 743 : 35= 21 ( ост 8) Значит в худшем случае, если бы в каждой клетке сидело по 21 кролику, ещё 8 кроликов были на свободе. Следовательно, если рассадить всех кроликов по клеткам, то по крайней мере в одной клетке будет сидеть не меньше 22 кроликов )
Эти подсчёты с кроликами и клетками в действительности связаны с важным математическим утверждением- принципом Дирихле.
Как можно сформулировать этот принцип?
Предположим, некоторое число кроликов рассажены в клетках. Если число кроликов больше, чем число клеток, то хотя бы в одной из клеток будет больше одного кролика.
В роли кроликов и клеток могут быть другие предметы.
Самая популярная формулировка такая: если в «n» клетках сидит «n+ 1» или более зайцев, то найдётся клетка, в которой сидят , по крайней мере два зайца.
Если число клеток больше , чем число кроликов, то как минимум одна клетка пуста.
Ещё этот принцип называют « принцип выдвижных ящиков» :
Если в «n» ящиках имеется не меньше, чем « n+1» вещь, то, открывая эти ящики, мы хотя бы в одном обнаружим не меньше двух вещей.
III. Решение задач.
№ 1. В школе 375 учеников. Докажите, что среди учащихся этой школы обязательно найдутся хотя бы два ученика, отмечающих свой день рождения в один и тот же день.
№ 2. В классе 30 человек. Саша Иванов сделал в диктанте 13 ошибок, а остальные- меньше. Докажите, что по крайней мере 3 ученика сделали ошибок поровну ( может быть по 0 ошибок)
( Обсуждение: здесь « зайцы- ученики, « клетки»- число сделанных ошибок.
В клетку 0 « посадим» всех, кто не сделал ни одной ошибки,
в клетку 1 – тех, у кого одна ошибка,
в клетку 2- - две ошибки
….. до 13 клетки, куда попал один Саша Иванов.
Теперь применим принцип Дирихле. Предположим, что никакие три ученика не сделали по одинаковому числу ошибок, то есть в каждую из « клеток» 0, 1, 2,… 12 попало меньше 3 учеников. Тогда в каждой из них 2 ученика или меньше, а всего в 13 клетках 2×13= 26 человек да + Саша Иванов, всё равно не будет 30 человек. Делаем вывод)
№ 3. Коля подсчитал, что за день в завтрак, обед и ужин он съел 10 конфет. Докажите, что хотя бы один раз он съел не меньше четырёх конфет.
№ 4. На девяти деревьях сидят 25 птиц. Докажите, что на каком- то дереве сидит не меньше трёх птиц.
Решение: Пусть на каждом дереве меньше трёх птиц, тогда всего на 9 деревьях не более, чем 18 птиц, а по условию их 25
Вывод: найдётся хотя бы одно дерево, на котором будет не меньше трёх птиц.
IV. Итог урока.
1) Познакомить с биографией Дирихле- немецкого математика.
2) Рефлексия- по карточкам.
V. Задание на дом.
1) Творческое задание: придумать задачи, которые решаются по принципу Дирихле.
2) № 133 из « М-6»
Занятие № 7.
Тема « Решение задач»
Занятие- практикум.
Цель: учить решать задачи путём логических рассуждений, умозаключений, применяя
принцип Дирихле.
План.
I. Повторение материала прошлого занятия.
А) теория.
1) В чём суть принципа Дирихле:
- - с « клетками» и « зайцами»;
- - с выдвижными ящиками;
- - если n>m.
Б) Проверить творческие задания.
В) Рассмотреть № 133 « М-6»
II. Решение задач.
Литература « Математика. Задачи на смекалку», автор Шарыгин И.Ф.
Стр 44
№ 181- самостоятельно, один объясняет с места.
№ 184- работа парами.
№ 186- самостоятельно, затем один объясняет
№ 189- работа группой, обмен мнениями.
№ 190- один на доске.
Решение:
1) 20+17-25=12 не менее стольких человек занимаются английским и плаванием.
2) 25-12=13 в классе не больше 13, а 14 человек занимаются в математическом кружке.
Вывод: в классе найдётся хотя бы один ученик, который увлекается всем.
III. Итог занятия.
Занятие № 8.
Тема « Понятие вероятности»
Цель: сформировать у учащихся представление о вероятности наблюдаемого события
; вспомнить виды событий. Дать понятие о независимых и зависимых
испытаниях ; благоприятных исходах событий.
План.
I. Повторение пройденного материала.
1) В чём заключается принцип Дирихле ?
2) № 133 из « М-6» - работа парами, объясняют друг другу.
II. Знакомство с новым материалом.
1) Беседа. В нашей речи и речи окружающих нас людей очень часто приходится слышать:
- « Я случайно достал билет на футбольный матч»
- « Я случайно встретил своего друга детства»
- « ну , если вы приобрели магнитофон завода А, то очень вероятно, что работать он будет очень хорошо»
Давайте вспомним виды событий.
Что каждое событие показывает ?
2) Лабораторная работа.( Работа парами)
А) Подбрасывают монету, записывают результат.
Б) Подбрасывают кубик, записывают результат.
Вопрос: число выпадений больше когда?
- « орла» на монете или
- четырёх очков на кубике
Какой вывод можно сделать?
Вывод: с увеличением числа подбрасываний значения статистической частоты
выбранного исхода устойчиво сосредотачивается возле некоторого числа «р»,
которое и называют вероятностью наблюдаемого исхода события.
Обратить внимание учащихся на то, что на практике статистические испытания и наблюдения являются основным способом оценки вероятностей событий.
3) Предлагаем обсудить спор трёх ребят: ребята провели опыты по подбрасыванию монеты. Из 100 раз « орёл» выпал 46 раз, « решка»- 54 раза. Ребята поспорили, что вероятней появится при следующем бросании: « орёл» или « решка» ?
- « Вероятней появление «орла»,- сказал Егор,- ведь до этого эксперимента он выпадал реже, чем « решка», значит теперь должен выпадать чаще»
-« Вероятней появится « решка»,- сказал Лёва,- раз она выпадала чаще, то и будет выпадать чаще.»
- « Появление « орла» и « решки» равновероятно,- сказала Наташа,- так как результат каждого следующего случайного эксперимента не зависит от результатов предыдущих».
С кем бы вы согласились и почему ?
Идёт разговор , дискуссия.
Разберём мнение каждого ученика.
Егор- это типичная « бытовая» трактовка закона больших чисел, то есть частота события стремится к вероятности с увеличением числа опытов.
Лёва- нельзя совсем не согласиться и с ним. Оказывается искомую вероятность можно вычислить.
Проблема: вероятность каких событий надо посчитать?
Наташино мнение о равновероятности событий обосновывается независимостью испытаний.
Как это ? Независимость испытаний?
Беседа. В теории вероятности есть два испытания ( опыта): независимые и зависимые.
Пример. В урне три шара с номерами № 1, № 2, № 3. Из урны последовательно извлекают два шара.
Испытания можно проводить двумя способами:
1 способ: извлекаем первый шар ( первое испытание), записываем его номер, шар кладём обратно в урну. Затем шары перемешиваем и извлекаем второй шар ( второе испытание) В этом случае результаты испытаний никак не влияют друг на друга.
Такие испытания называют независимыми.
2 способ: извлекают первый шар, но в урну его не возвращают, а сразу за ним извлекают второй. В этом случае исходы второго испытания зависят от того, какой исход имел место в первом испытании.
Такие испытания называют зависимыми.
Дать понятие о благоприятных исходах событий ( испытаний) .
Приводят свои примеры независимых и зависимых событий.
А как же вычислить вероятность события ? Это тема следующего занятия.
( если будет время на уроке , то взять формулу)
III. Итог занятия.
Свои примеры.
Занятие № 9
Тема « Формула вероятности событий»
Цель: познакомить с формулой вероятности событий. Дать понятие условной
вероятности. Показать операции с событиями: сумма двух событий,
произведение двух событий. Дать определение несовместимых событий.
План.
I. Вспомним материал прошлого занятия.
1) Привести свои примеры вероятности наблюдаемого события, разобрать их.
2) Рассмотреть зависимые и независимые события.
II. Знакомство с новым материалом.
1. Уходя с прошлого занятия, мы поставили перед собой вопрос: как вычислить вероятность события?
1)Вернёмся к задаче с урной с шариками.
( В урне три шара № 1, №2, № 3 )
1 способ: испытания независимые.
Вынимаем первый шар. Какова вероятность, что попадётся шар № 2 ?
Это
Кладём его обратно, берём второй шар. Какова вероятность, что попадётся шар № 3 ?
Это
Получаем формулу:
Число благоприятных исходов, m
Вероятность события
Число всех равновозможных исходов, n
= 
Определение: Вероятностью события называется отношение числа случаев,
благоприятствующих событию, к общему числу всех равновозможных
случаев.
2 способ: испытания зависимые.
Вынимаем первый шар. Вероятность
, убираем его. Вынимаем второй шар- вероятность 
( так как во время второго испытания в урне находятся только 2 шара)Задача. Какова вероятность события появления чётного числа при бросании игрального кубика?
Решение: На гранях числа 1, 2, 3, 4, 5, 6. Из них три чётных, поэтому число благоприятных случаев равно 3. Число всех равновероятных случаев равно 6. Тогда вероятность появления граней с чётным числом равна
.Вывод:
1. Вероятность случайного события есть положительное число, заключённое
между нулём и единицей, то есть положительная правильная дробь.
2. Вероятность достоверного события равна 1.
3. Вероятность невозможного события равна 0.
Задача. В урне находится 38 совершенно одинаковых по размеру шаров, отличающихся друг от друга только цветом: 8 белых, 12 чёрных, 10 красных, 3 синих, 5 коричневых. Из урны вынимают наугад один шар. Какова вероятность появления цветного ( не белого и не чёрного ) шара?
Решение: Всего шаров n=38.
Цветных шаров m= 10+3+5=18.
В.с.=
2 способ: 1) Вероятность появления красного шара равна
- синего шара равна
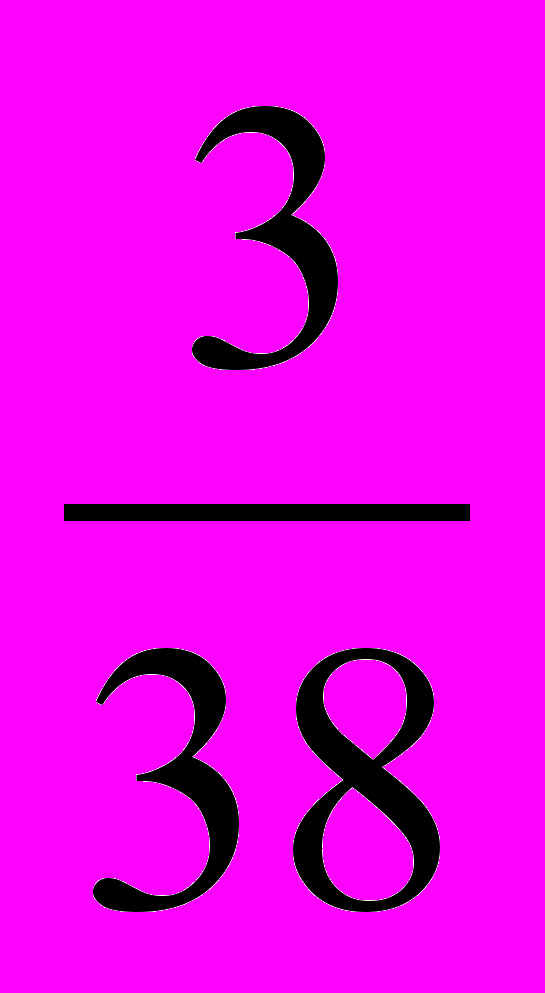
- коричневого шара
2. Дать понятие о несовместимых событиях и совместного появления двух независимых событий.
Определение: события называют несовместимыми, если появление одного из них
исключает появление других событий в одном и том же испытании.
Пример: брошена монета.
События « появился орёл» и « появилась решка» - несовместимые.
Это же событие называем независимым.
Рассмотрим пример совместного появления двух независимых событий.
Пример: Брошены два игральных кубика. Какова вероятность одновременного появления шестёрок на обоих кубиках?
Решение: Рассмотрим все возможные случаи.
Составим таблицу: ( первое число- на 1 кубике, второе число- на 2 кубике)
| (1 ;1) | (1; 2) | (1; 3) | (1; 4) | (1; 5) | (1; 6) |
| (2; 1) | (2; 2) | (2; 3) | (2; 4) | (2; 5) | (2; 6) |
| (3; 1) | (3; 2) | (3; 3) | (3; 4) | (3; 5) | (3; 6) |
| (4; 1) | (4; 2) | (4; 3) | (4; 4) | (4; 5) | (4; 6) |
| (5; 1) | (5; 2) | (5; 3) | (5; 4) | (5; 5) | (5; 6) |
| (6; 1) | (6; 2) | (6; 3) | (6; 4) | (6; 5) | (6; 6) |
Из таблицы видно, что вероятность одновременного появления двух шёстёрок равна
Как можно получить этот результат по другому.
Решение:
- появление шестёрки на первом кубике.- вероятность появления шестёрки на втором кубике.Вывод: Вероятность совместного появления двух независимых событий равна
произведению вероятностей этих событий.
3. А если проводятся зависимые испытания, то в этом случае говорим об условной вероятности.
Вернёмся к урне, где были шары № 1, № 2, № 3 .
Если проводим два независимых друг от друга испытания, то справедливо правило умножения вероятностей, что они произойдут вместе
Если зависимые испытания, то условная вероятность тоже вычисляется умножением, но исход 1 испытания умножаем на исход 2 испытания, то есть
В
События
ывод:
несовместимые
совместимые
Вероятность появления одного из них, безразлично какого, равна сумме вероятностей этих событий
независимые
зависимые
Вероятность появления двух событий равна произведению вероятности событий
Условная вероятность
4. Примеры.
l
1 l2 l3 l4 l5A B C
Укажите, какие из изображённых на рисунке событий являются совместными, а какие- несовместными?
Решение: А и В – совместные ( общий исход l3)
А и С – совместные ( общие исходы l1 и l5)
В и С – несовместные ( нет общих исходов)
III. Итог занятия.
1) Повторить основные понятия .
2) Правило сложения и умножения вероятностей.
3) Формула вычисления вероятностей.
Дома: придумать примеры на вычисление вероятности событий.
Занятие № 10
Тема « События и вероятности. Решение задач»
Цель: вспомнить основные понятия событий и вероятностей. Учить решать задачи на
вычисление вероятности события.
План.
I. Теоретический турнир.
Тест- закончить предложение.
1. События бывают …
2. Вероятностью события называется …
3. Формула выглядит так …
4. Вероятность случайного события есть число …
5. Вероятность достоверного события равна …
6. Вероятность невозможного события равна …
7. События называют несовместимыми, если появление одного из них …
8. Совместные испытания разделяют на два вида …
II. решение задач.
№ 1. Лотерея состоит из 1000 билетов, среди них 150 выигрыш. Вынимается произвольный билет из 1000. Чему равна вероятность того, что этот билет выигрышный?
Решение: n= 1000, m= 150
В.с.=
; В.с.=
;№ 2. В полученной партии деталей оказалось 200 деталей первого сорта, 100 деталей второго сорта, 50 деталей третьего сорта. Наудачу вынимается одна из деталей. Чему равны вероятности получить деталь первого, второго, третьего сорта?
Решение: n= 200+100+50
n = 350
В.с.=
- 1 сорта;В.с.=
- 2 сорта;В.с.=
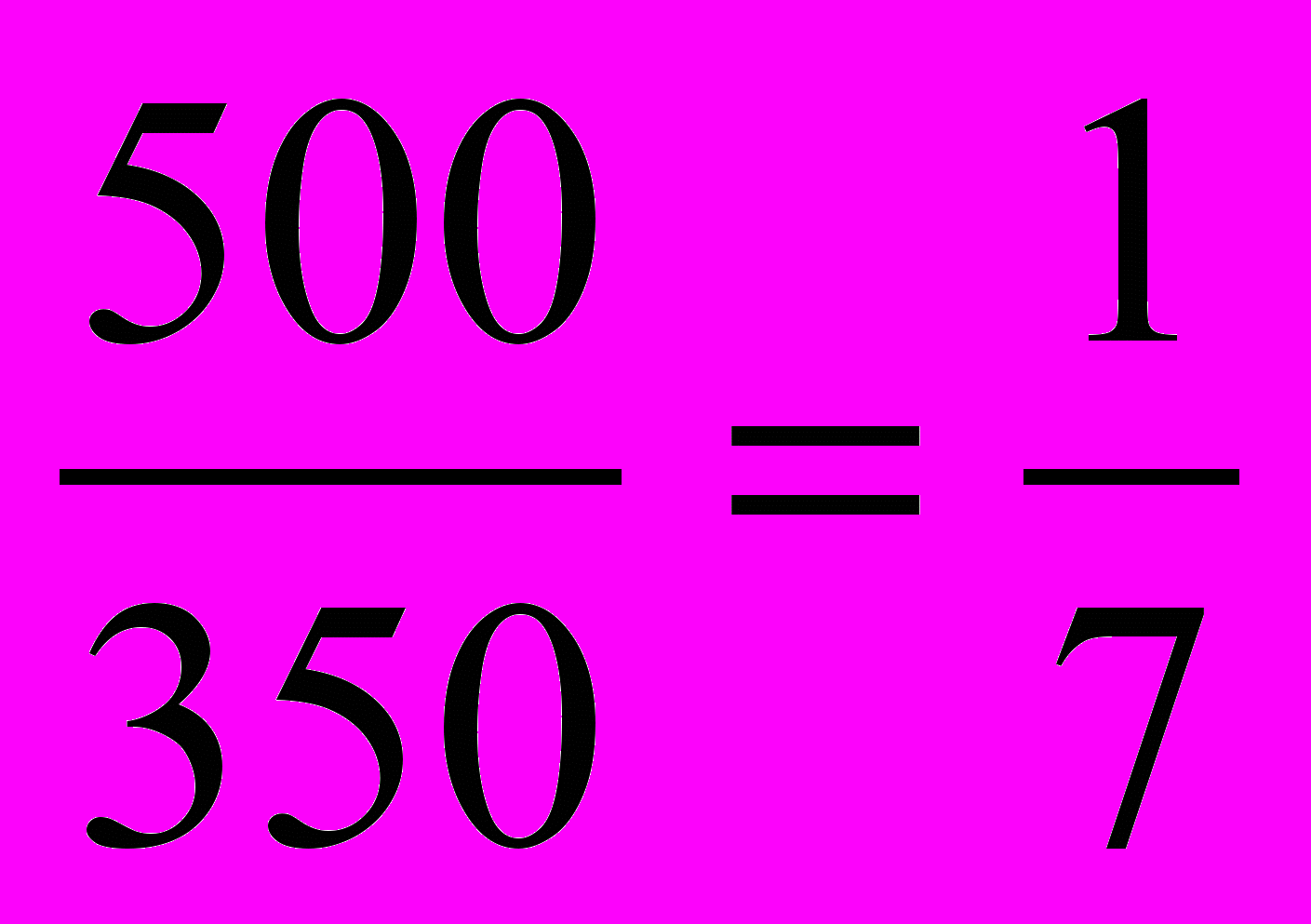-3 сорта.№ 3. Рассмотрим пример.
А) Я загадала, что первый прохожий, которого мы увидим из окна, будет мужчина. Какова вероятность, что я отгадала?
( В.с.=