Geum.ru

Учебно-методический комплекс. Рабочая программа для студентов специальности 036401. 65 «Таможенное дело» форма обучения очная

Вид материалаУчебно-методический комплекс

Содержание


II семестр.
8. Образовательные технологии.
9. Учебно-методическое и информационное обеспечение дисциплины (модуля).
Подобный материал:
1   2   3   4

II семестр.

3.1. Первообразная. Неопределённый интеграл, его свойства. – 2 ч.

Методы замены переменной и интегрирования по частям.– 2 ч.
    1. Определённый интеграл и его свойства. Теорема о среднем значении. Интеграл с

переменным верхним пределом. Формула Ньютона – Лейбница – 2 ч.

Методы замены переменной и интегрирования по частям. Вычисление длин и площадей

с помощью определённого интеграла – 2 ч.

3.3. Дифференциальные уравнения. Дифференциальные уравнения с разделяющимися

переменными. – 2 ч.

Линейные дифференциальные уравнения с постоянными коэффициентами. – 2 ч.

4.1. Введение в теорию вероятностей. Непосредственный подсчет вероятностей. – 2 ч.

Теоремы сложения и умножения вероятностей. Условная вероятность. – 2 ч.

Формула полной вероятности. Формулы Байеса - 2 ч.

4.2. Повторение испытаний, формула Бернулли, Муавра – Лапласа, Пуассона. -2 ч.

4.3. Случайные величины, функция распределения, плотность ве­роятности.– 2 ч.

Числовые характеристики случайной величины. Законы распределения.– 2 ч.

4.4. Основы математической статистики. Генеральная совокупность и выборка,

числовые характеристики выборки. – 2 ч.

То­чечные и интервальные оценки ха­рактеристик генеральной совокупности – 2 ч.

4.5. Проверка статистических гипотез – 2 ч.

4.6. Элементы корреляционно-регрессионного анализа – 2 ч.

Уравнение линейной регрессии. – 2 ч.


6. Планы семинарских занятий.

I семестр.

1.1. Действия с матрицами – 2 ч.

Вычисление определителей, нахождение обратной матрицы – 4 ч.

1.2. Решение системы линейных алгебраических уравнений, формулы Крамера. - 2 ч.

Решение системы линейных уравнений методом исключения – 2 ч.

Ранг матрицы, применение теоремы Кронекера-Капелли к исследованию СЛАУ – 2 ч.

1.3. Линейные операции над векторами. Скалярное произведение векторов. – 2 ч.

Линейная зависимость векторов – 2 ч.

1.4. Координаты точки на плоскости. Уравнения прямой на плоскости. – 2 ч.

Угол между прямыми, точка пересечения прямых. Расстояние от точки до прямой.– 2 ч.

Эллипс, гипербола, парабола, их канонические уравнения и свойства – 2 ч.

2.1. Комплексные числа – 2 ч.

2.2. Предел числовой последовательности – 2 ч.

2.3. Предел функции. Виды неопределённостей. – 2 ч.

Точки разрыва и их классификация. – 2 ч.

2.4. Дифференцирование функций. Правило Лопиталя. – 4 ч.

Применение производной к исследованию функций. – 2 ч.

II семестр.

3.1. Первообразная и неопределённый интеграл. – 2 ч.

Методы замены переменной и интегрирования по частям.– 2 ч.

3.2. Вычисление определенного интеграла. Вычисление площадей с помощью определённого

интеграла – 4 ч.

3.3. Дифференциальные уравнения с разделяющимися переменными. – 2 ч.

Линейные дифференциальные уравнения с постоянными коэффициентами, характеристическое уравнение – 2 ч.

4.1. Основы комбинаторики. Непосредственный подсчет вероятностей. – 2 ч.

Теоремы сложения и умножения вероятностей. – 2 ч.

Условная вероятность. Формула полной вероятности. Формулы Байеса - 2 ч.

4.2. Повторение испытаний, формула Бернулли, Муавра – Лапласа, Пуассона. -2 ч.

4.3. Числовые характеристики случайной величины..– 2 ч.

Законы распределения.– 2 ч.

4.4. Генеральная совокупность и выборка. То­чечные оценки параметров генеральной

совокупности – 2 ч.

Интервальные оценки параметров генеральной совокупности – 2 ч.

4.5. Проверка статистических гипотез – 2 ч.

4.6. Элементы корреляционно-регрессионного анализа – 2 ч.

Уравнение линейной регрессии. – 2 ч.


7. Учебно - методическое обеспечение самостоятельной работы студентов. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины (модуля).


Вопросы к экзамену. I семестр
  1. Матрицы. Виды матриц. Действия с матрицами.
  2. Определители и их свойства.
  3. Обратная матрица.
  4. Ранг матрицы. Определение ранга матрицы.
  5. Решение систем линейных уравнений. Формулы Крамера, метод исключения.
  6. Теорема Кронекера-Капелли. Исследование решения СЛАУ.
  7. Однородные системы линейных алгебраических уравнений.
  8. Векторы, координаты вектора. действия над ними.
  9. Скалярное произведение векторов. Его геометрические при­ложения.
  10. Метод координат на плоскости. Виды уравнения прямой на плоскости. Угол между прямыми, условие параллельности и перпендикулярности прямых. Расстояние от точки до прямой.
  11. Канонические уравнения эллипса, гиперболы, параболы, их свойства.
  12. Множества и операции над ними. Комплексные числа.
  13. Числовые последовательности, предел последовательности.
  14. Функции. Предел функции в точке. Замечательные пределы.
  15. Непрерывность функции в точке. Свойства функций, непрерывных на отрезке.
  16. Производная функции, её геометрический смысл.
  17. Дифференцирование суммы, разности, произведения и частного.
  18. Дифференцирование сложной функции.
  19. Исследование функции на монотонность и экстремумы с помощью производной.
  20. Нахождение направлений выпуклости и точек перегиба функции.
  21. Асимптоты графика функции.



II семестр
  1. Неопределённый интеграл и его свойства.
  2. Вычисление неопределённого интеграла метод замены переменной.
  3. Вычисление неопределённого интеграла методом интегрирования по частям.
  4. Определённый интеграл и его свойства.
  5. Теорема о среднем значении.
  6. Интеграл с переменным верхним пределом.
  7. Формула Ньютона – Лейбница.
  8. Вычисление площади плоской фигуры с помощью определённого интеграла.
  9. Дифференциальные уравнения, порядок уравнения, задача Коши.
  10. Дифференциальные уравнения с разделяющимися переменными, линейные, однородные.
  11. Линейные дифференциальные уравнения с постоянными коэффициентами.
  12. Случайное событие, операции над событиями. Классическое определение вероятности.
  13. Относительная частота события. Статистическое определение вероятности.
  14. Теорема сложения вероятностей, следствия из неё.
  15. Теорема умножения вероятностей, следствия из неё.
  16. Условная вероятность.
  17. Дискретная случайная величина. Случайная величина, распределенная по биномиальному закону.
  18. Непрерывная случайная величина, плотность вероятности.
  19. Нормальный закон распределения.
  20. Числовые характеристики случайной величины.
  21. Числовые характеристики в случае биномиального и нормального законов распределения.
  22. Генеральная совокупность и выборка. Полигон, гистограмма. Эмпирическая функция распределения.
  23. Числовые характеристики выборки..
  24. Точечные оценки генеральных характеристик, их свойства. Выборочное среднее
    как точечная оценка математического ожидания.
  25. Выборочная дисперсия и исправленная выборочная дисперсия как точечные оценки
    дисперсии.
  26. Доверительный интервал. Точность и надёжность интервальной оценки. Их связь.
  27. Понятие статистической гипотезы. Основная и альтернативная гипотезы. Уровень
    значимости. Ошибки I и II рода.
  28. Понятия функциональной и корреляционной зависимости.
  29. Линейная регрессия.
  30. Коэффициент корреляции как измеритель линейности стохастической зависимости.



Примерные темы контрольных работ
  1. Действия с матрицами, вычисление определителя, решение СЛАУ по формулам Крамера, исследование СЛАУ.
  2. Действия с векторами, уравнение прямой на плоскости, точка пересечения прямых, угол между прямыми, канонические уравнения эллипса, гиперболы, параболы.
  3. Действия с комплексными числами, предел последовательности, предел функции, производная функции.
  4. Вычисление неопределенного интеграла, вычисление определенного интеграла, решение простейших дифференциальных уравнений.
  5. Непосредственный подсчет вероятностей, теоремы сложения и умножения вероятностей, полной вероятности, Байеса, Бернулли, Муавра-Лапласса, Пуассона.
  6. Закон распределения и числовые характеристики случайной величины, статистическое распределение выборки, оценки параметров статистического распределения.
  7. Определение параметров уравнения линейной регрессии.


Примеры контрольных работ

Контрольная работа № 1.

1. Вычислить выражение (А-В*)·А*, где , ;

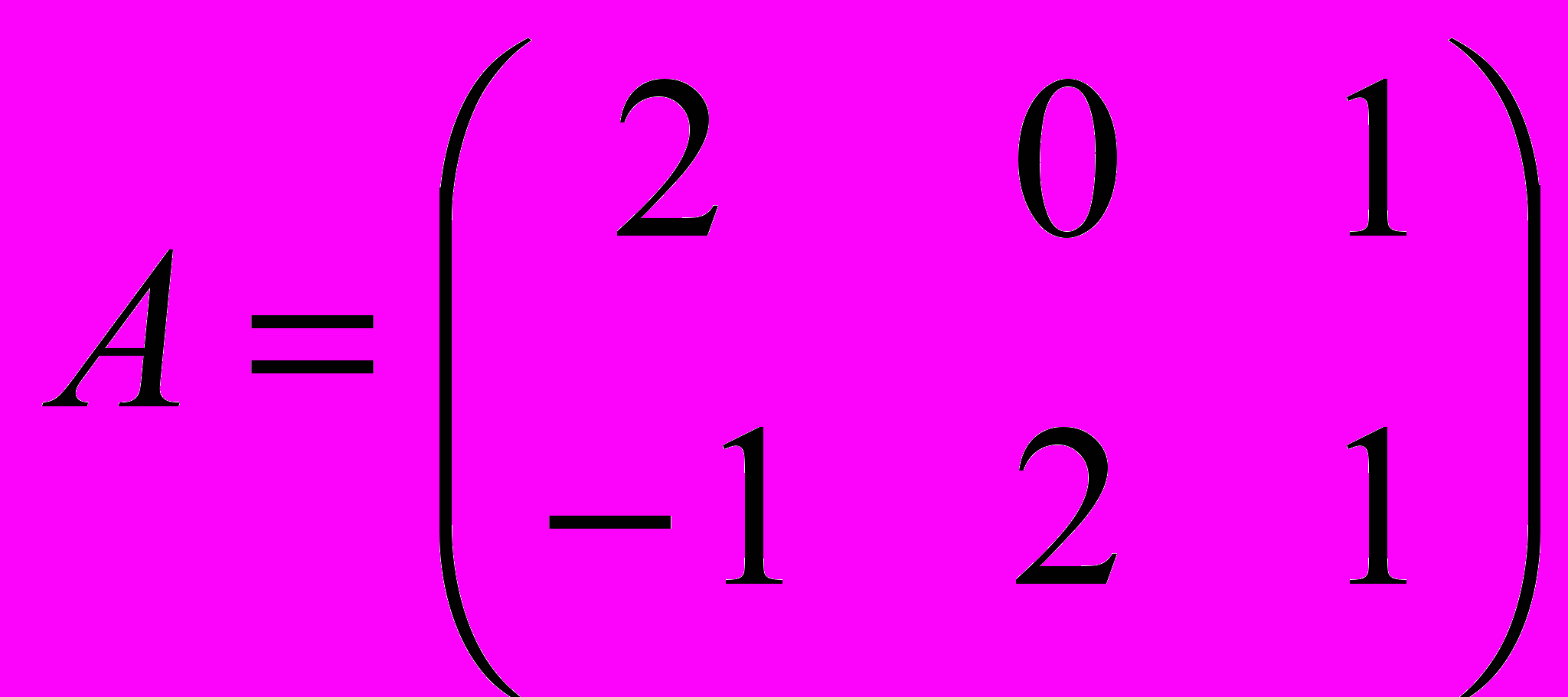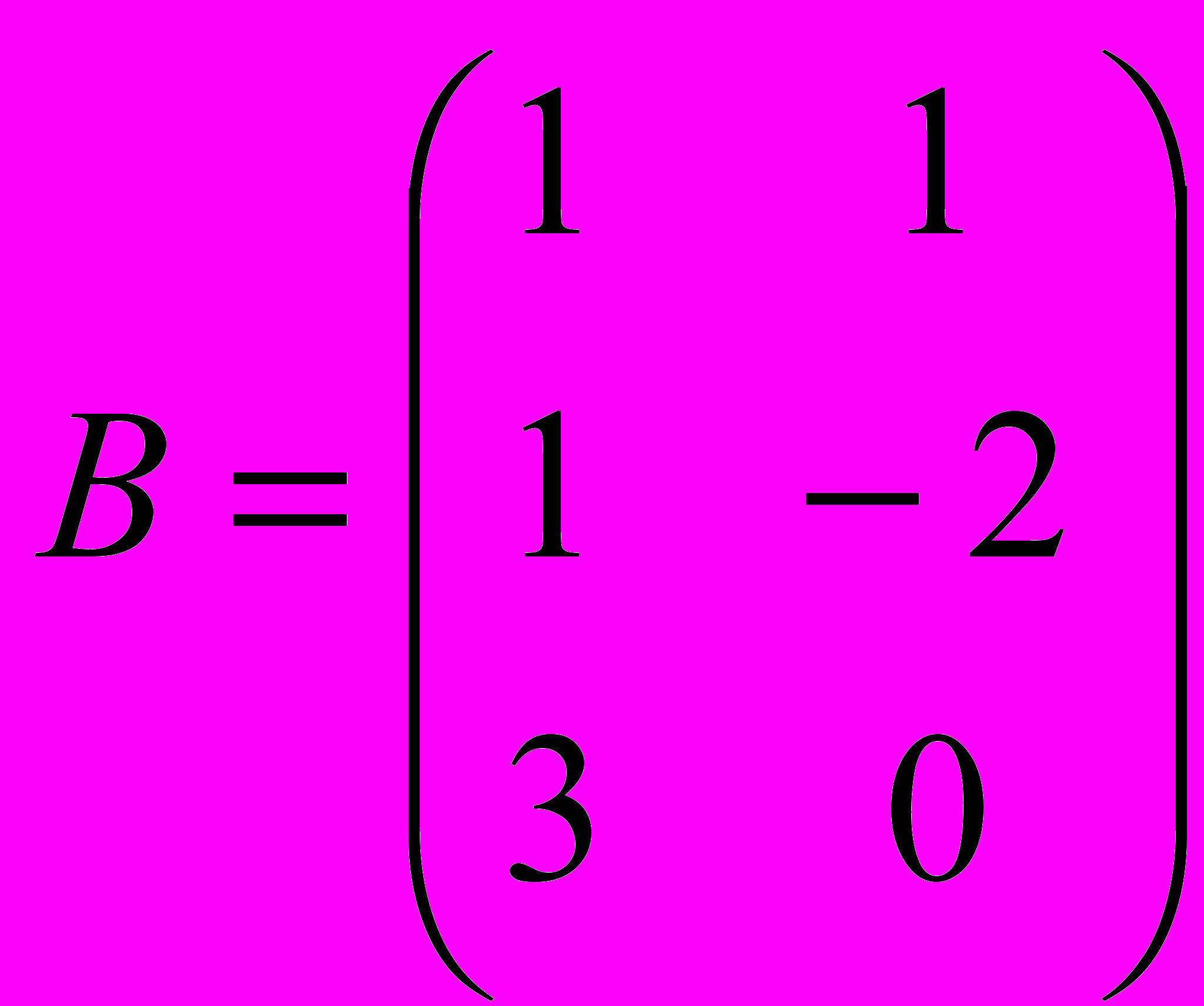2. Упростить и вычислить определитель .

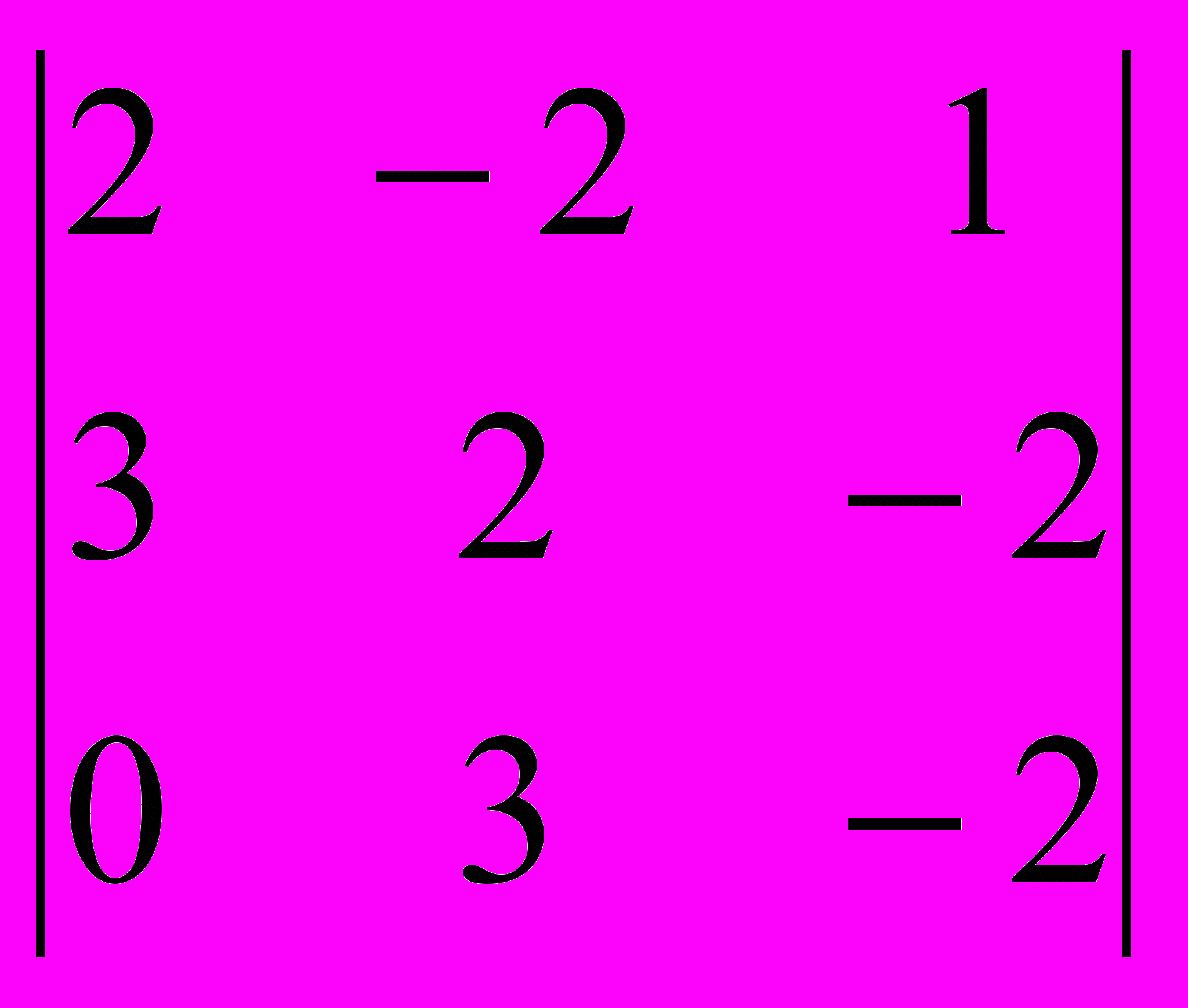3. Найти алгебраическое дополнение элемента а32 определителя из задания 2.

4. Используя формулы Крамера, решить систему линейных алгебраических уравнений

.

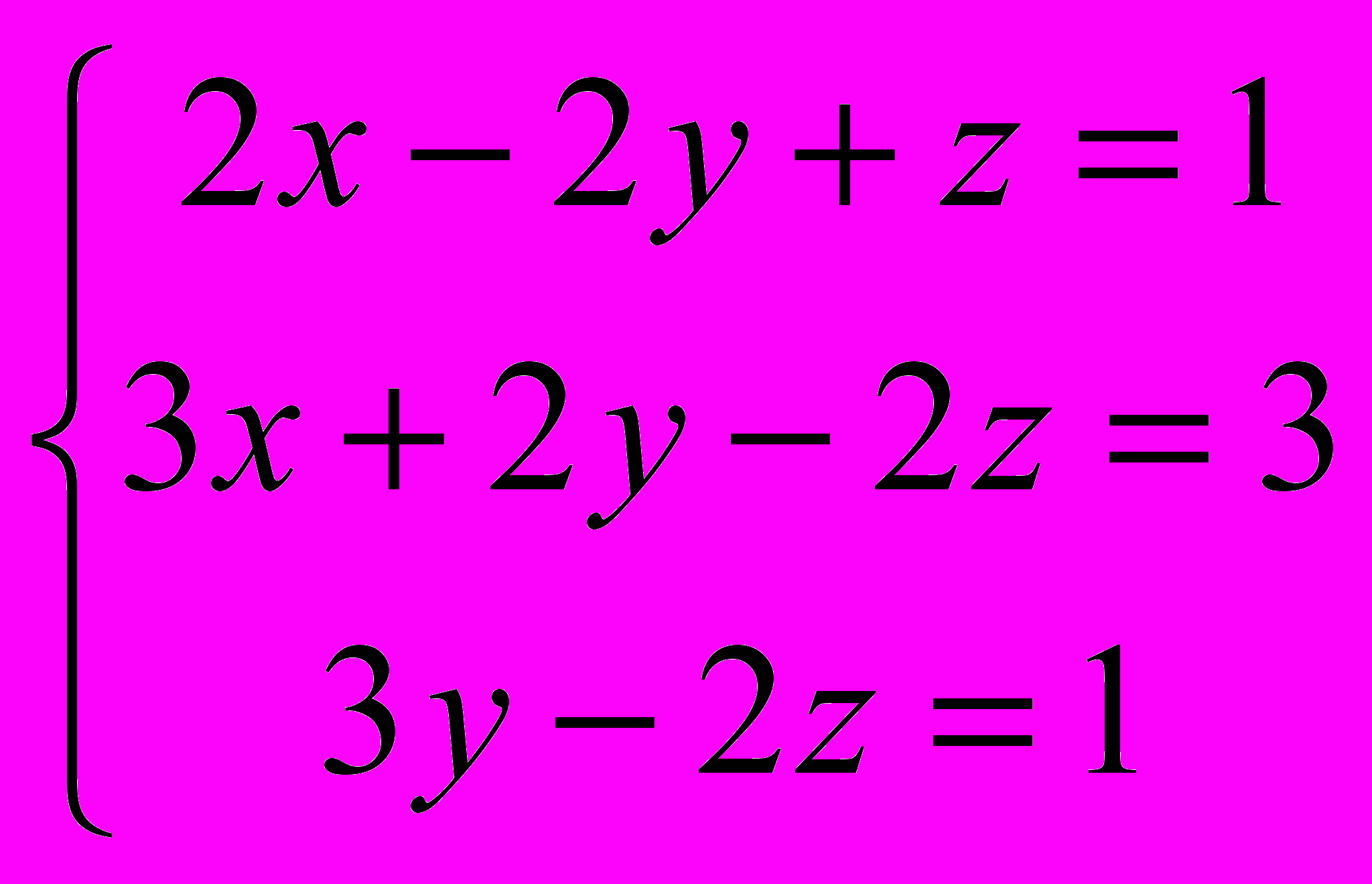5. Найти ранг матрицы .


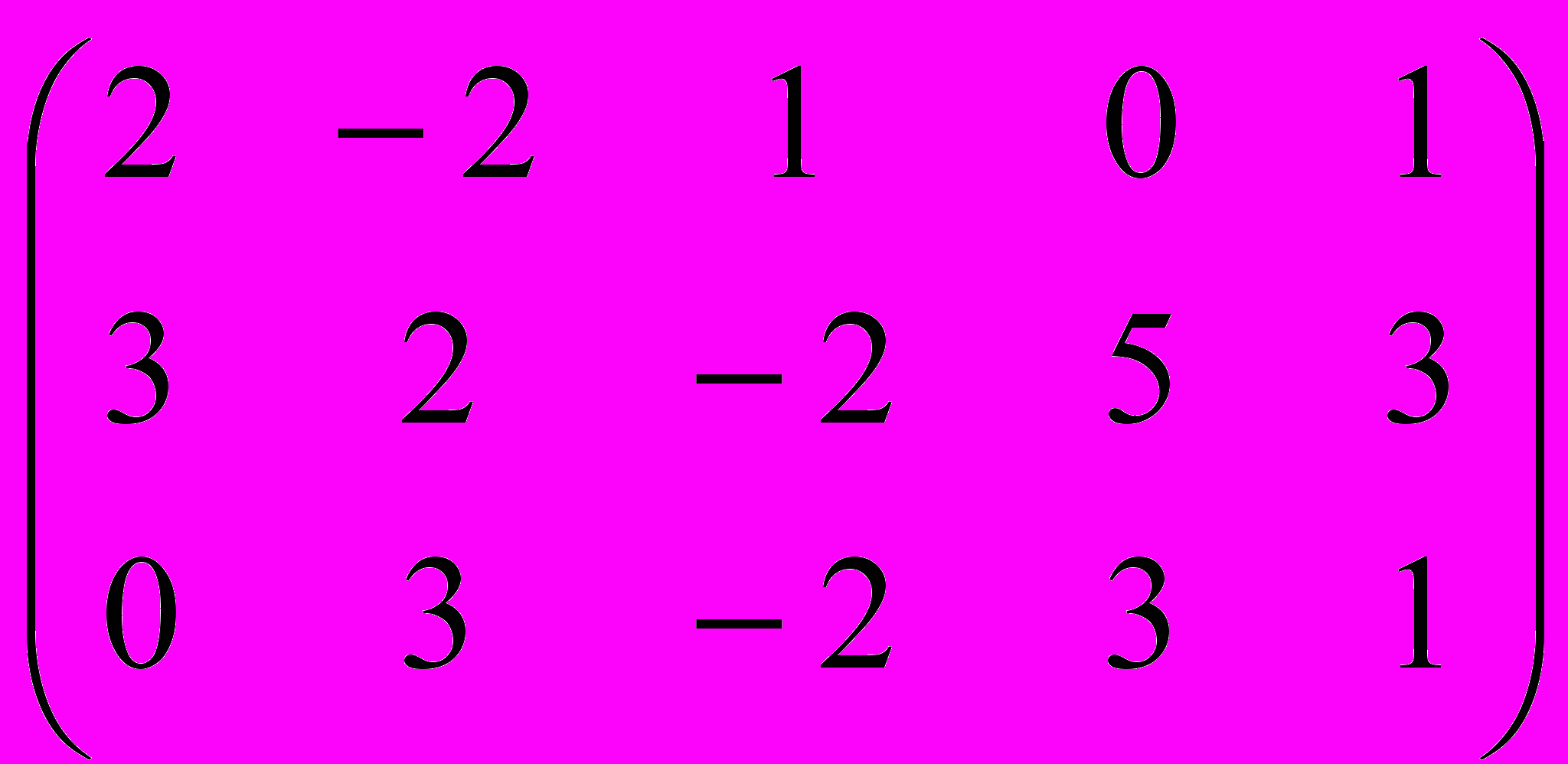Контрольная работа № 2.

1. Даны точки А(2, 2, 1), В(0, 4, 3) и С(1, 2, 4). Найти длину вектора АВ + 2ВС.

2. Даны векторы a = {2; 2; - 3}, b = {4; -2; -2}. Вычислить выражение (a+b)·(2a-b).

3. Дана прямая -2х + 3у – 6 = 0. Определить параметры k и b.

4. Даны точки А(1,2), В(3,3) и С(3,1). Найти высоту треугольника АВС, опущенную из вершины А.

5. Построить эллипс 9х2+25у2=225. Найти полуоси, координаты фокусов, эксцентриситет.


Контрольная работа № 3.

1. Дано: 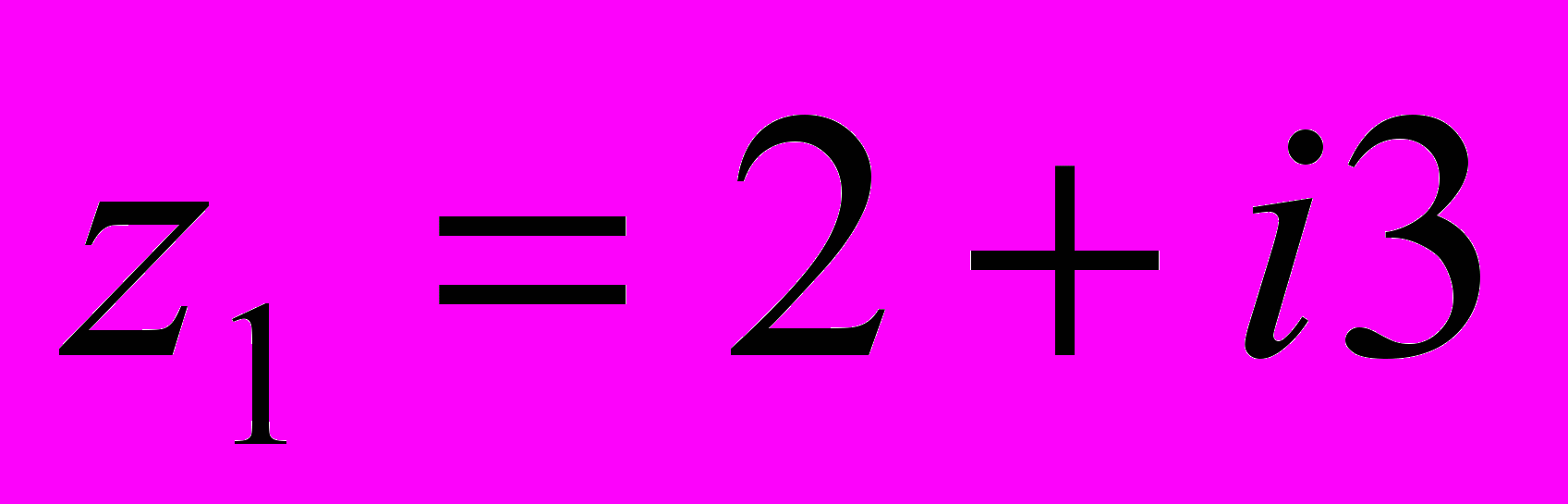, 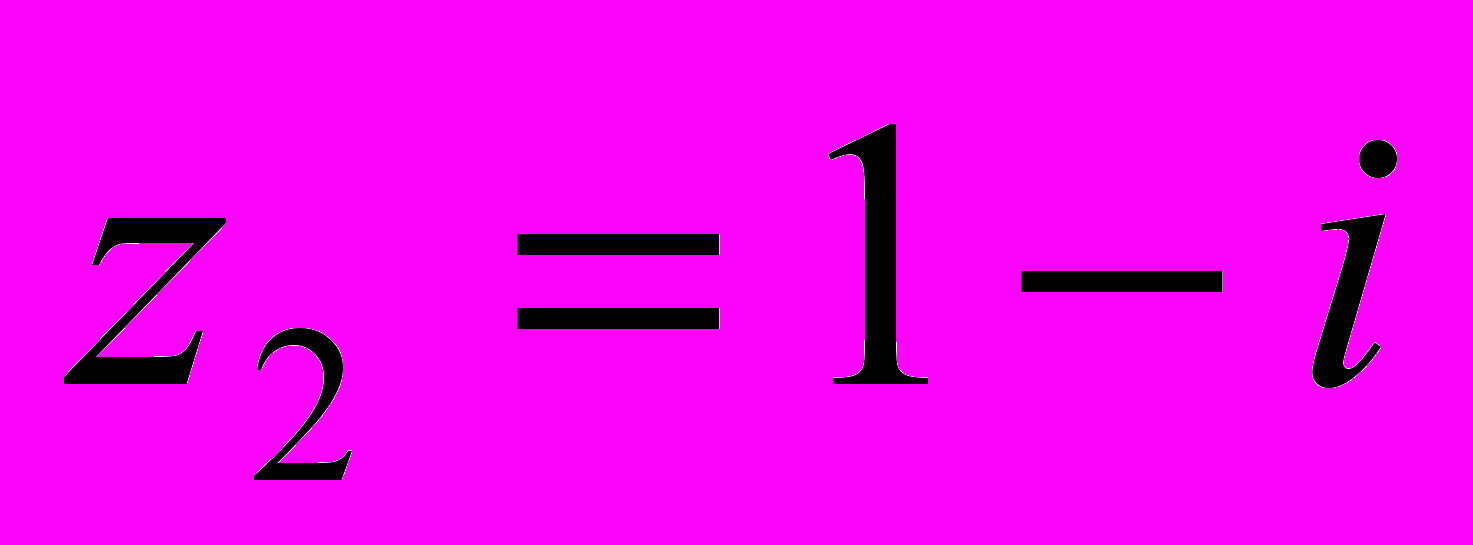. Вычислить: .

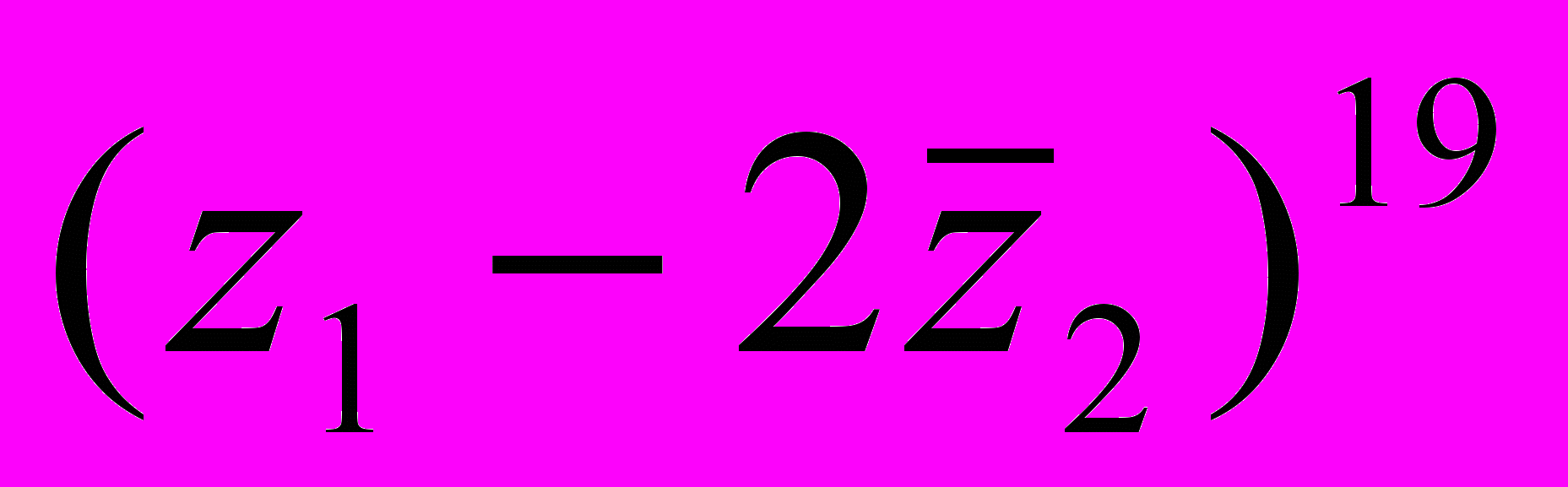2. Найти 5-й элемент последовательности xn+2 = n∙xn + xn+1, x1 = 1, x2 = 2.

3. Найти предел последовательности .

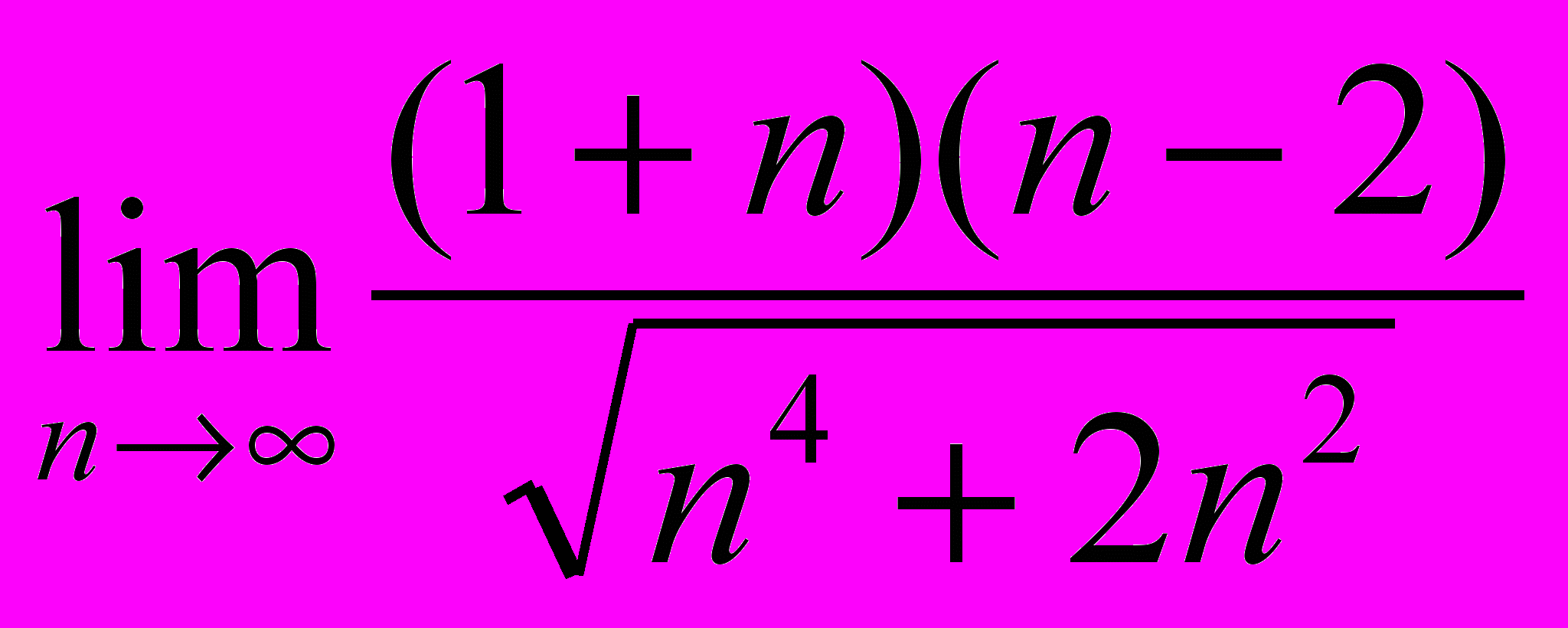4. Вычислить пределы , , , .

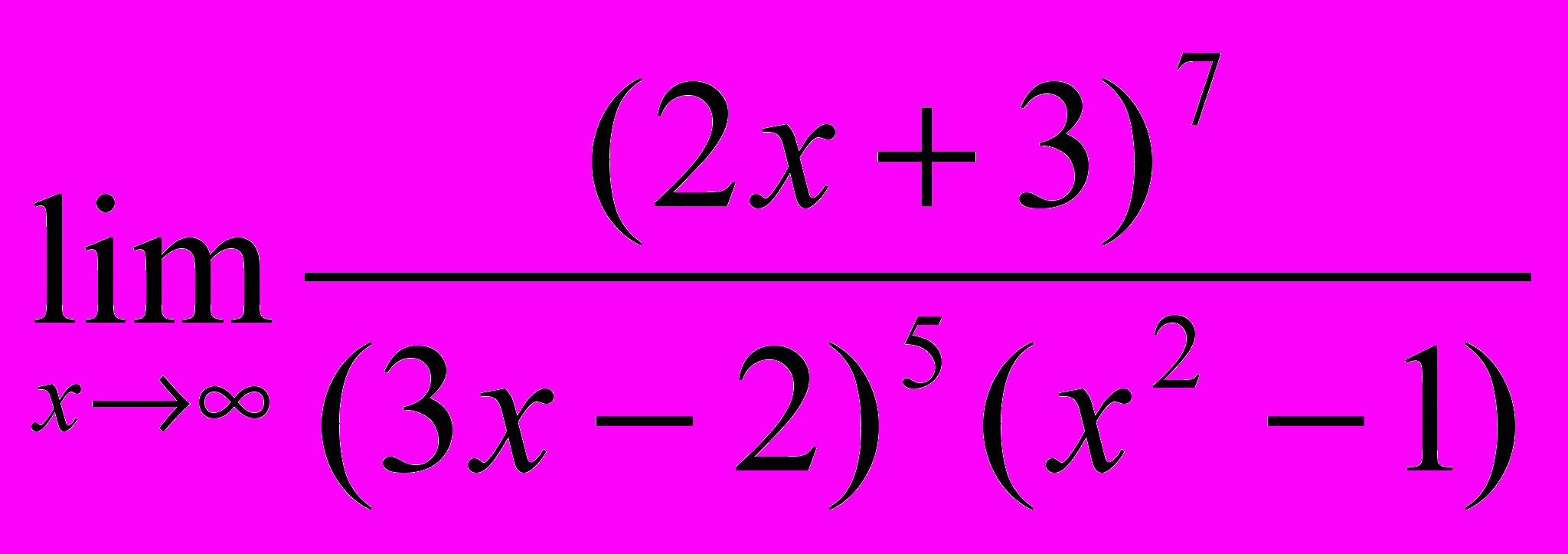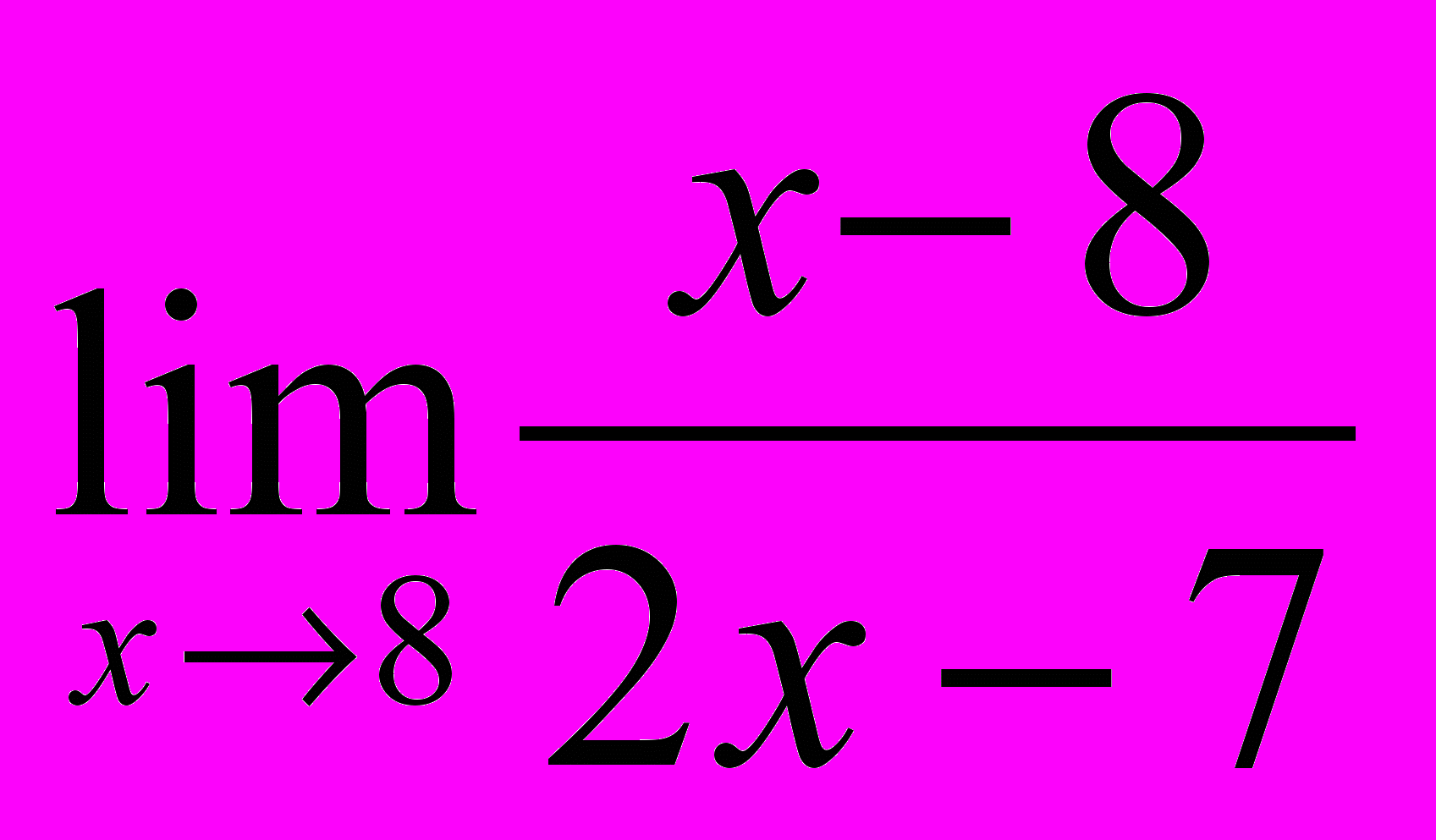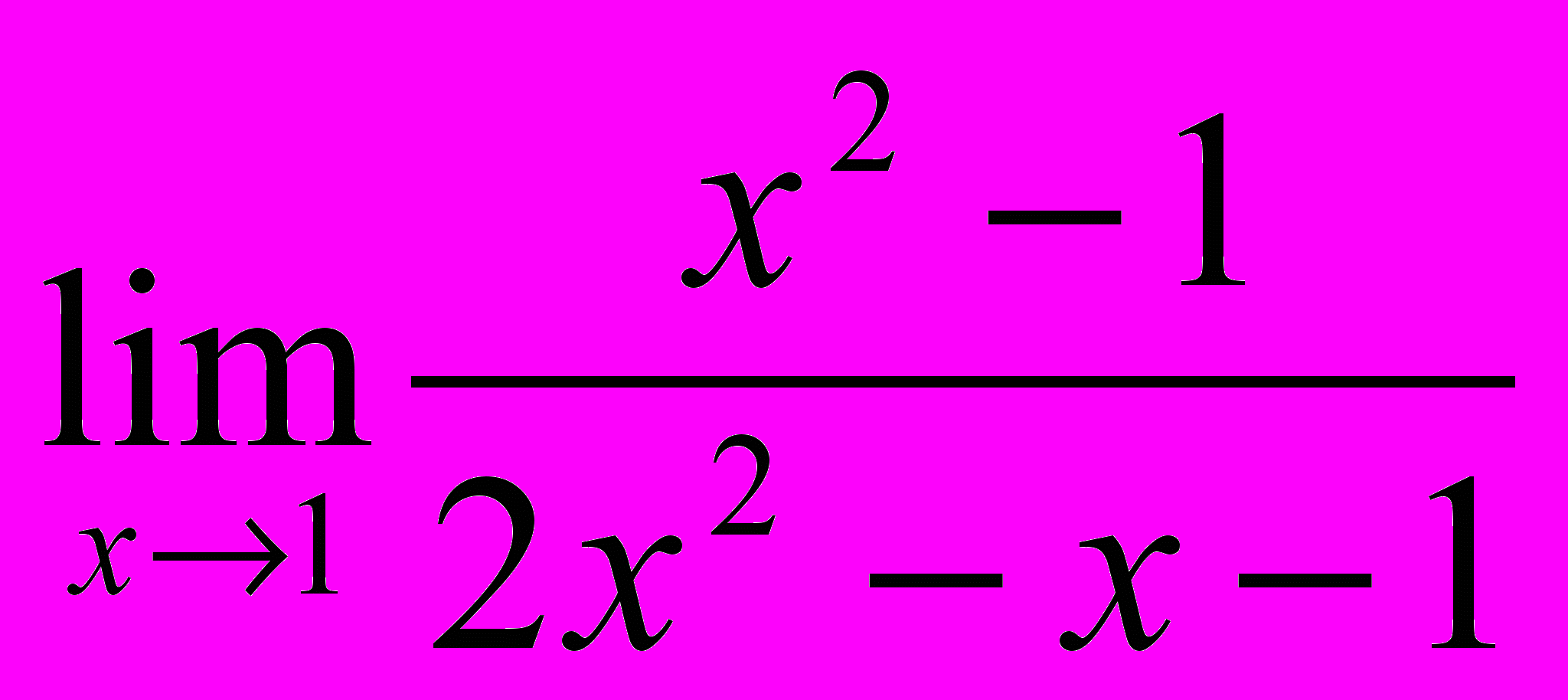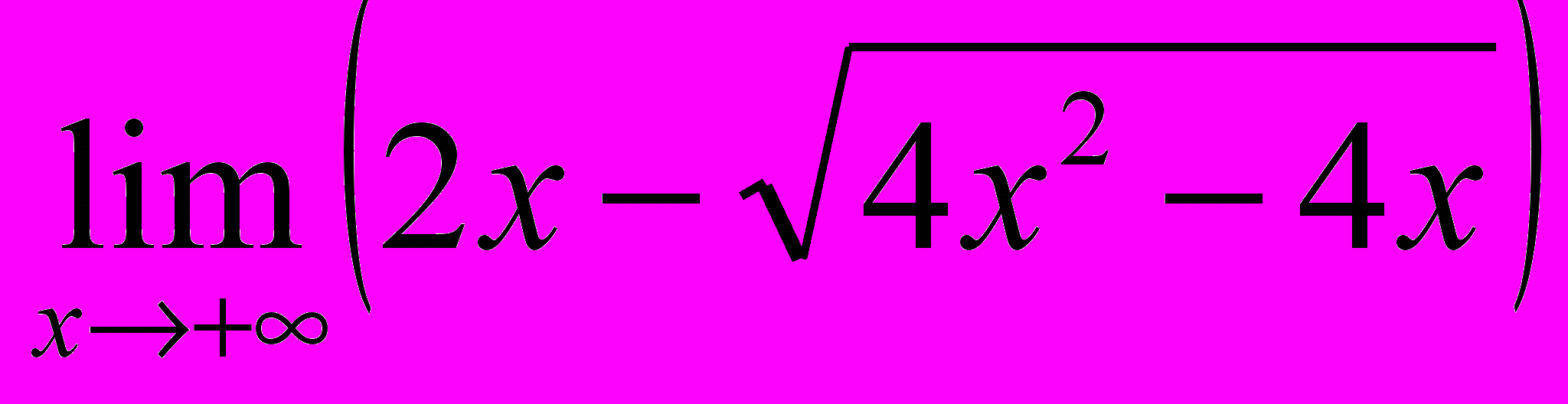5. Найти производные , , .


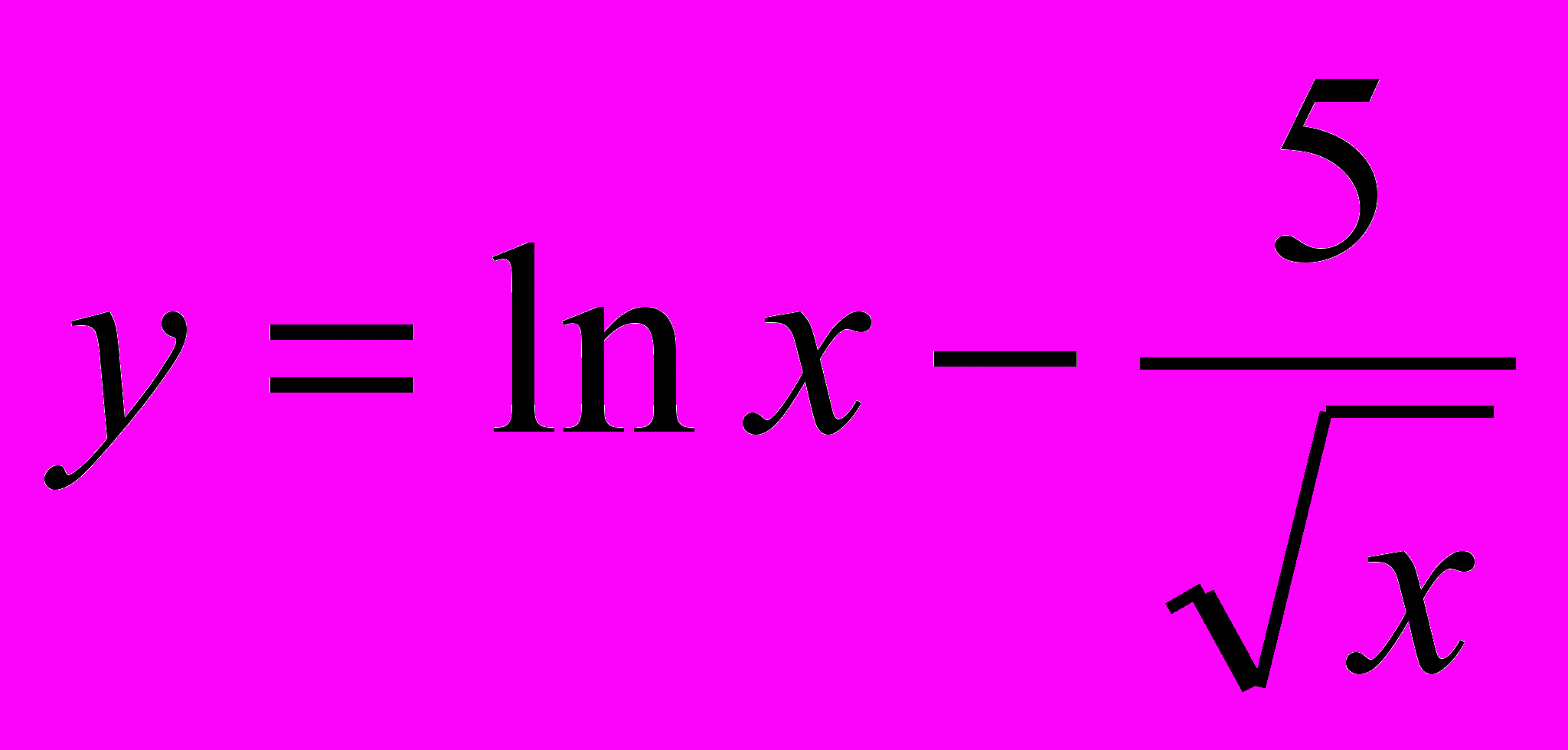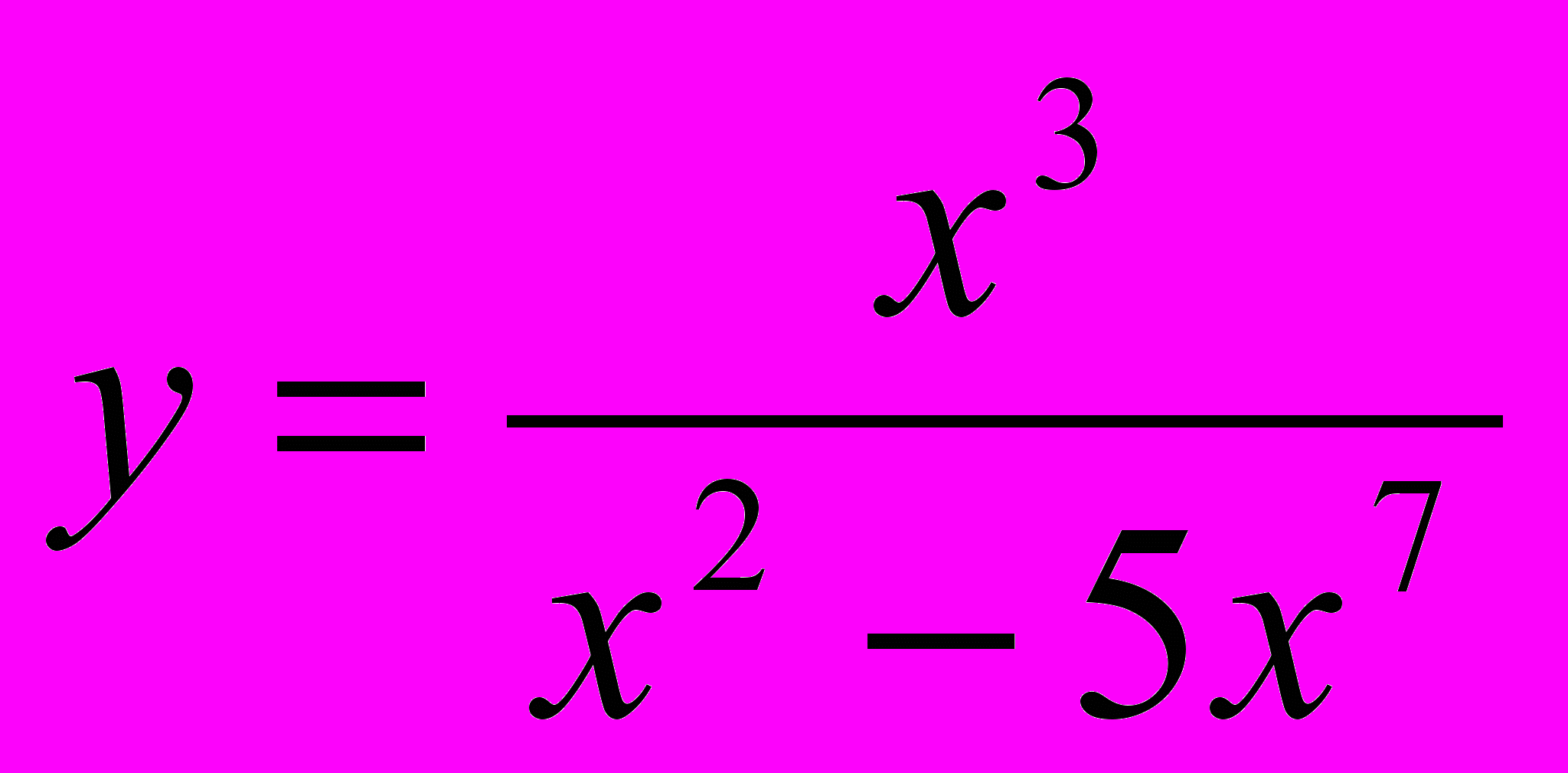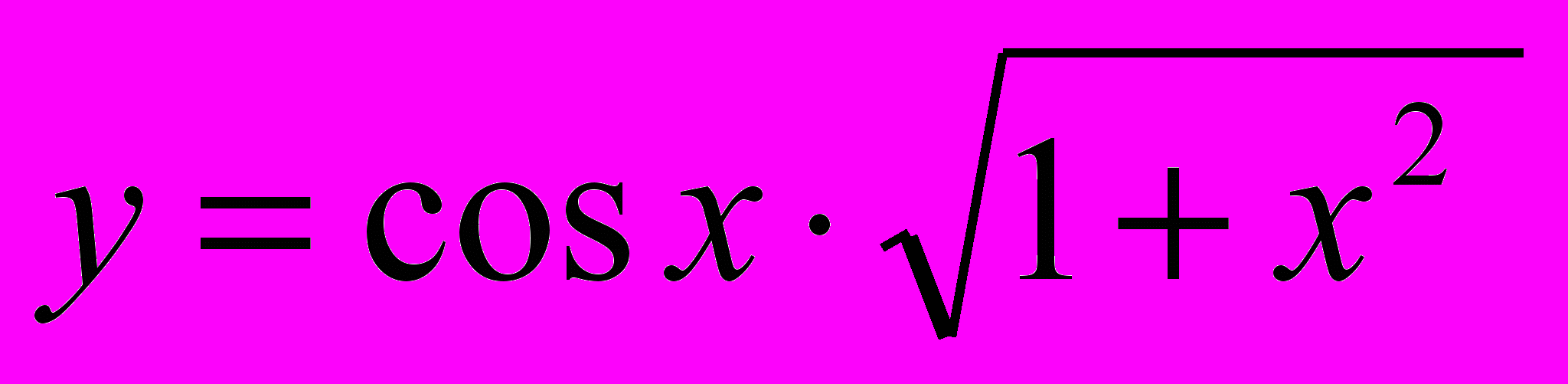Контрольная работа № 4.

1. Найти неопределенные интегралы , , ,

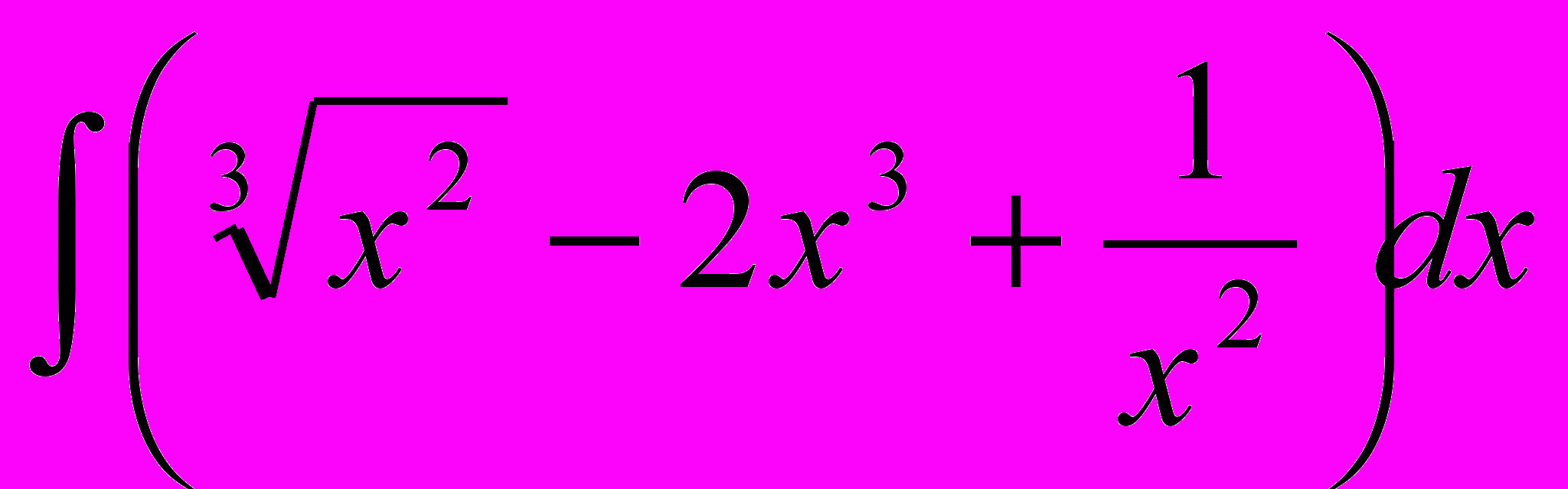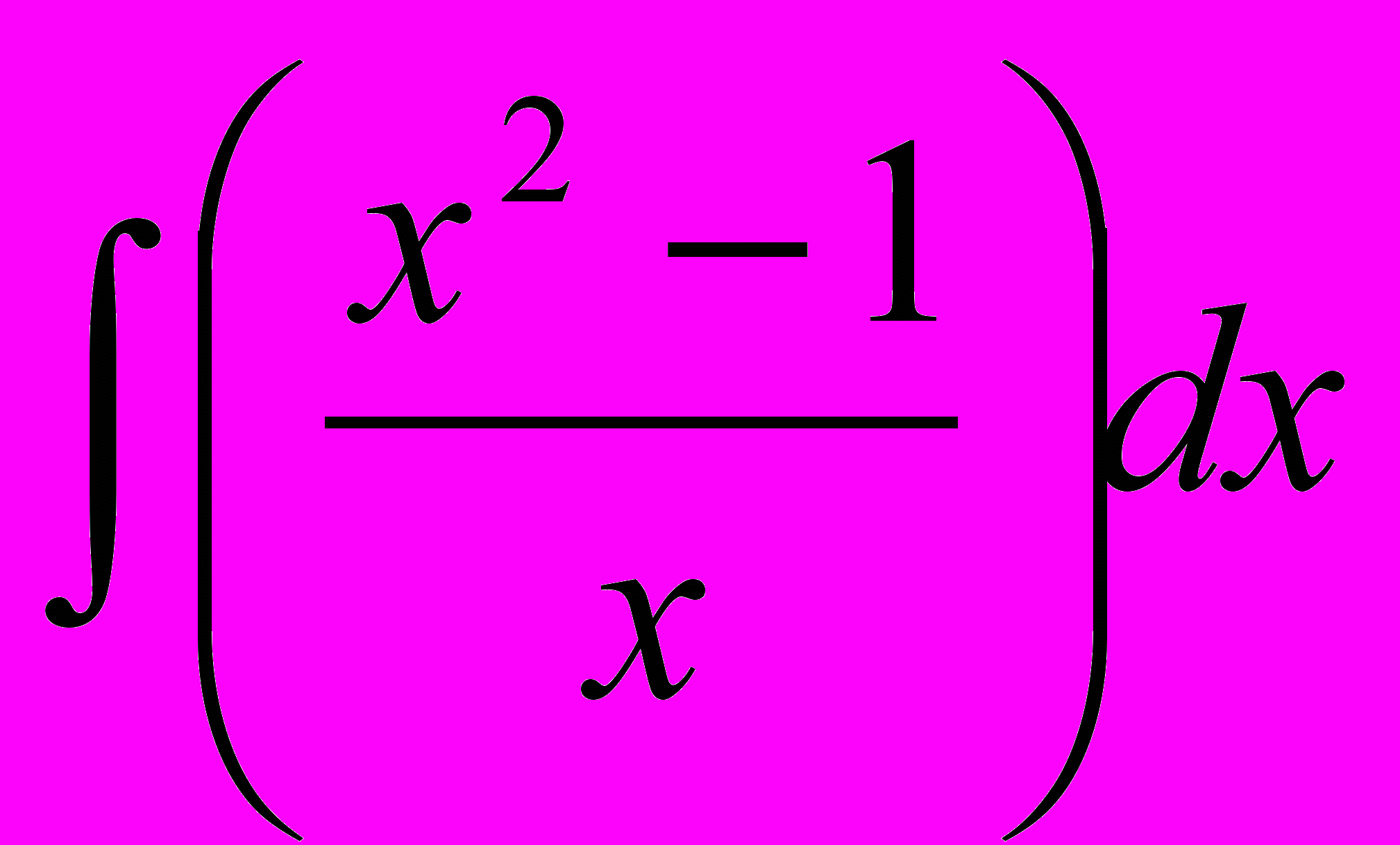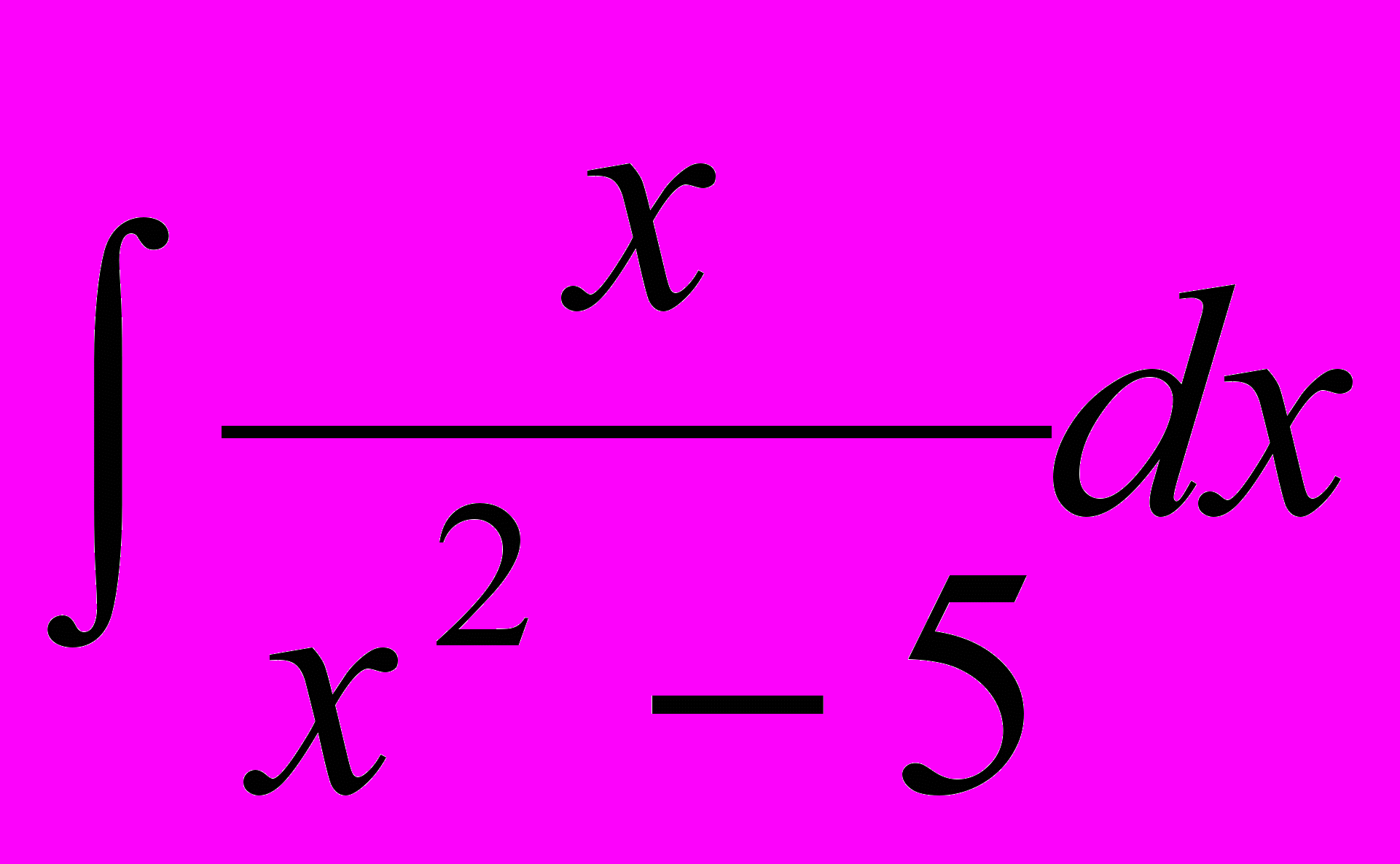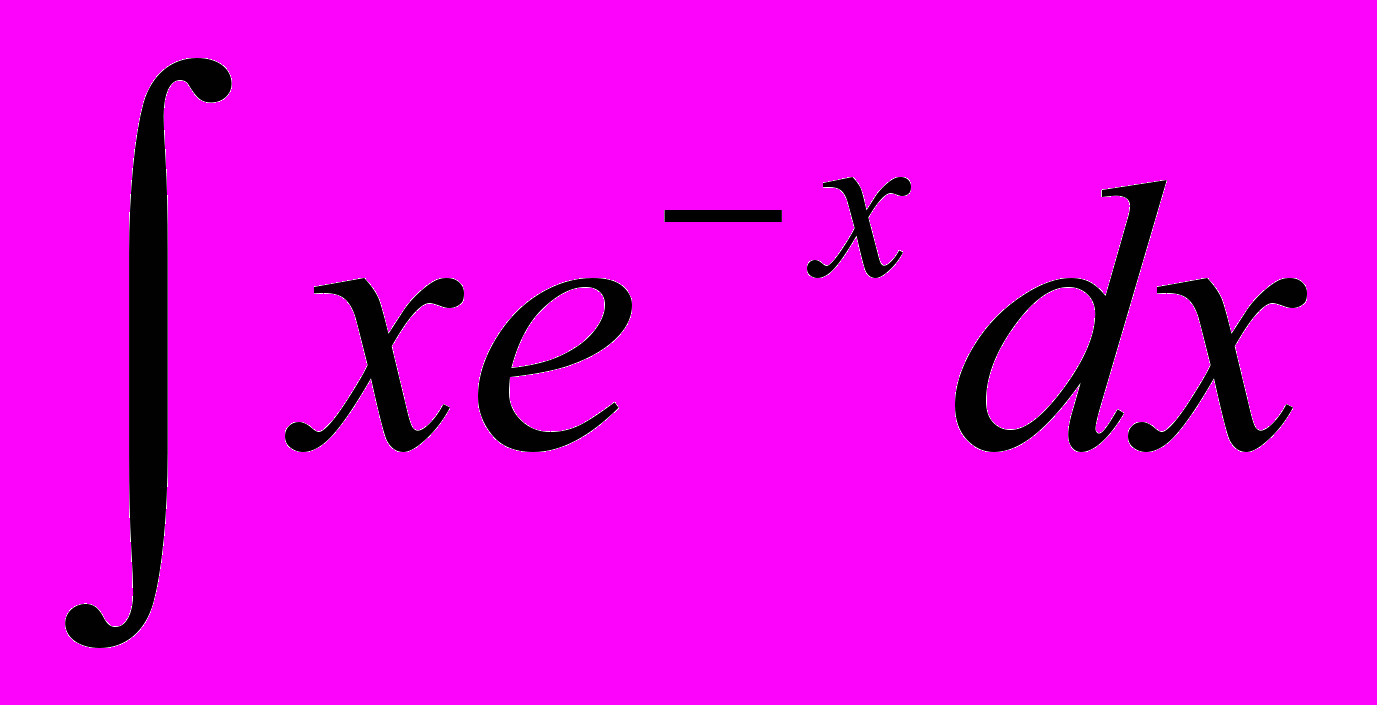
2. Вычислить определенные интегралы , .

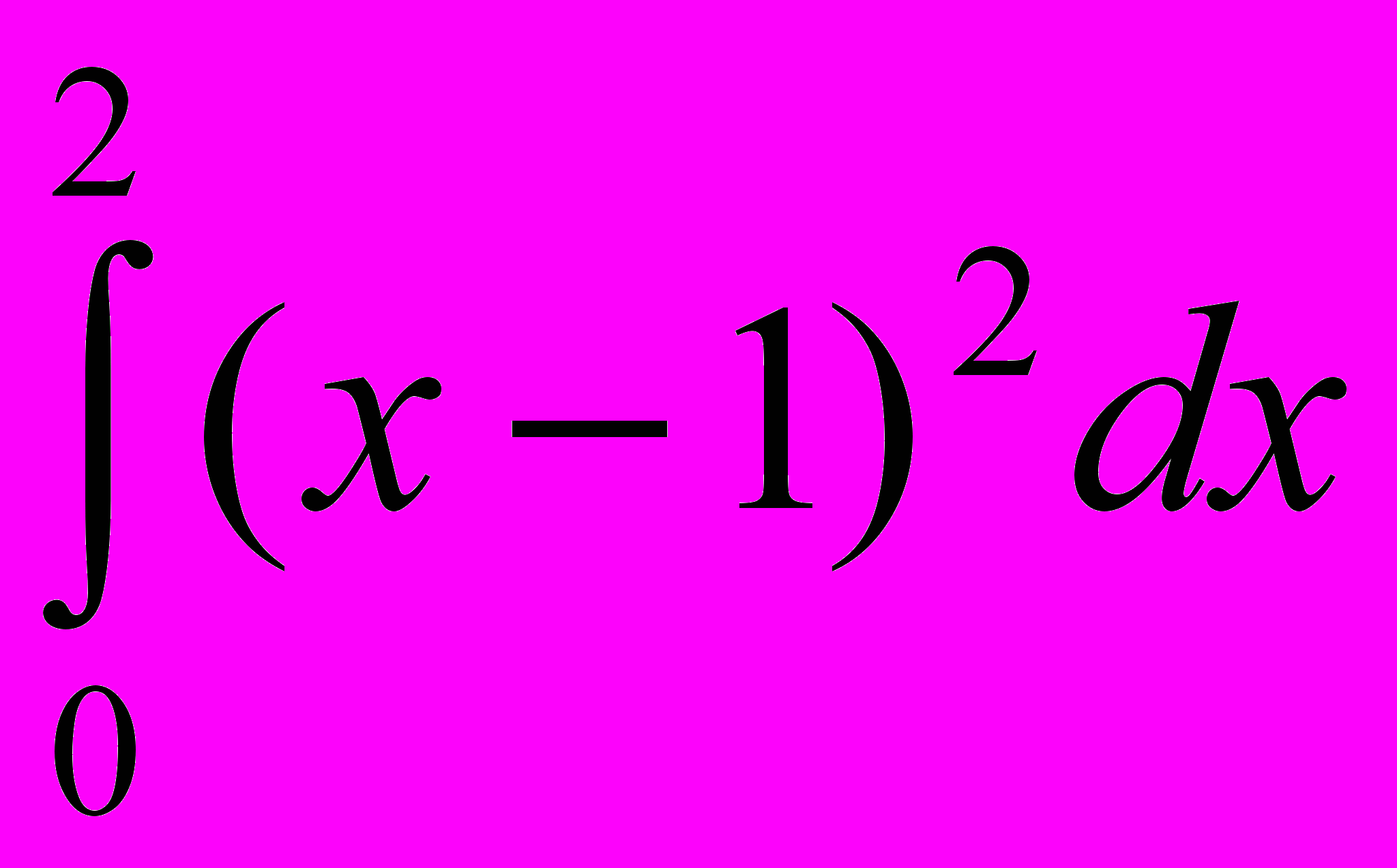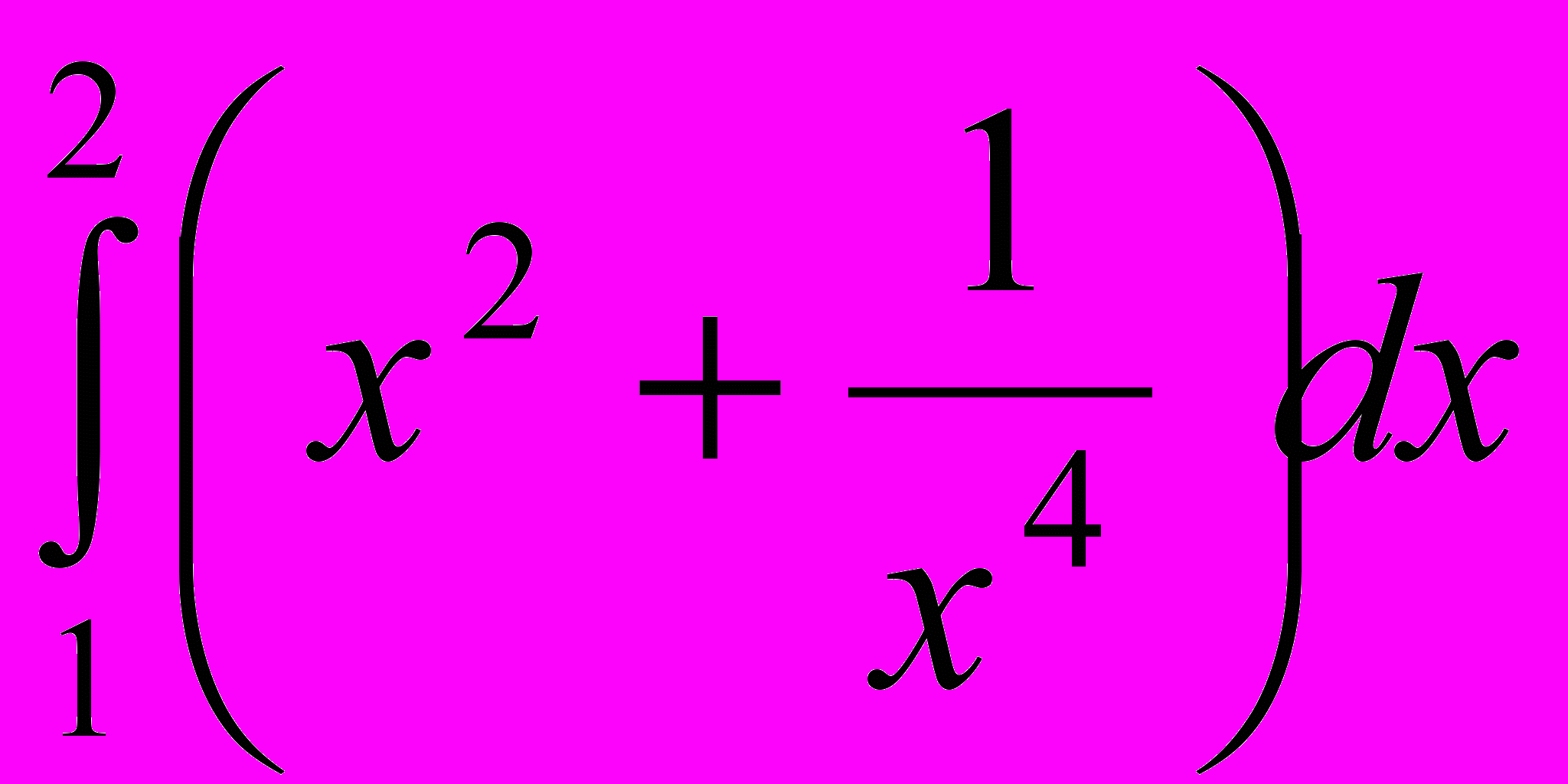3. Найти общее решение дифференциального уравнения


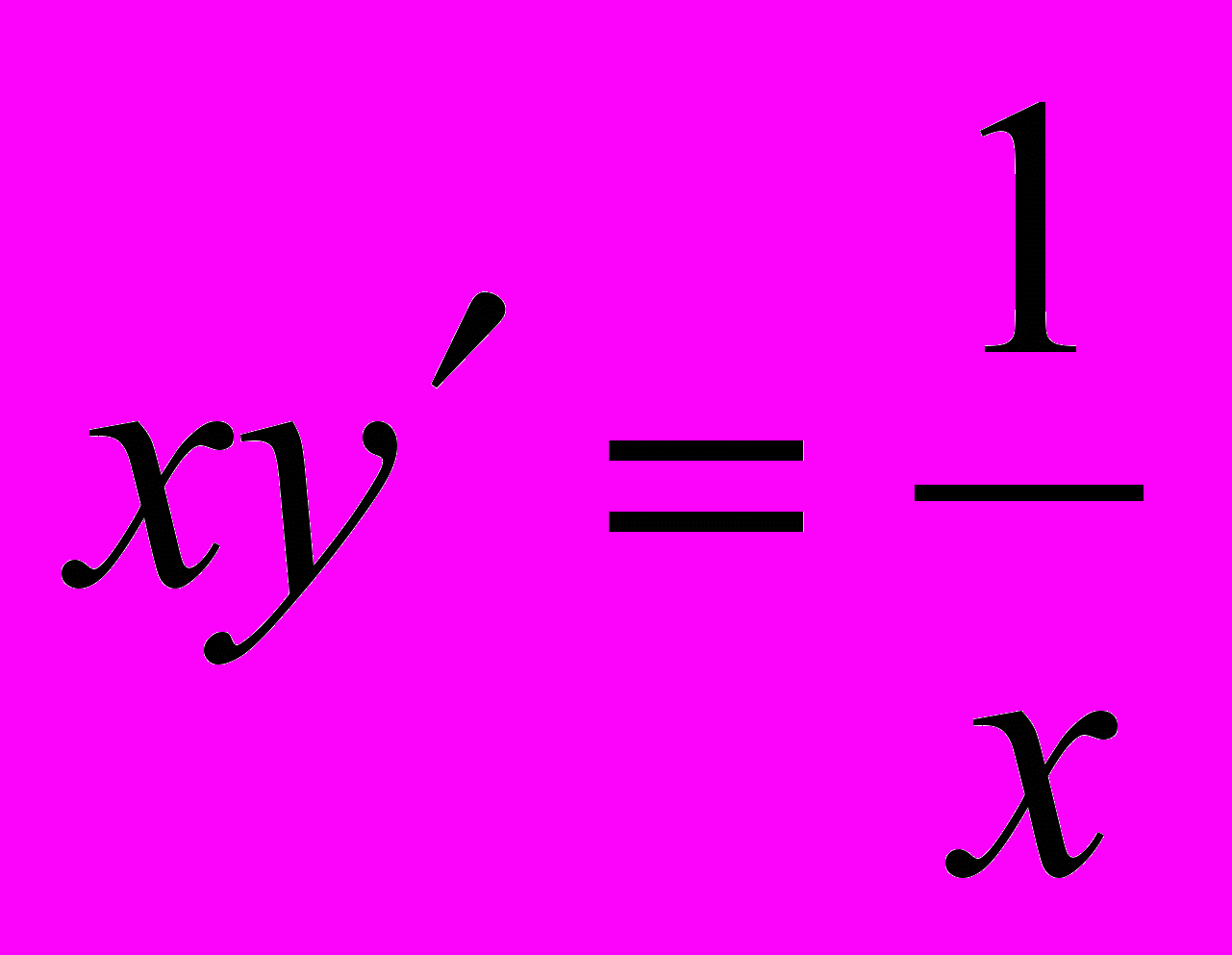
Контрольная работа № 5.
  1. Из пяти карточек с буквами А, Б, В, Г, Д наугад одна за другой выбираются три и располагаются в ряд в порядке появления. Какова вероятность, что получится слово «ДВА»?
  2. Из урны с 7 красными и 5 синими шарами берут наугад 3 шара. Какова вероятность того, что все взятые шары окажутся одного цвета?
  3. Устройство состоит из 3 независимо работающих элементов. Вероятность отказа каждого элемента в течение года равна 0,2. Определить а) вероятность отказа 2-х и более элементов; б) вероятность того, что не откажет ни один элемент.
  4. В первом ящике содержится 15 деталей, из них 10 стандартных; во втором — 10 деталей, из них 7 стандартных; в третьем — 20 деталей, из них 16 стандартных. Найти вероятность того, что на­удачу извлеченная деталь из наудачу взятого ящика — стандартная.
  5. Вероятность попадания в цель в каждом выстреле одинакова и равна 0,7. Производится 150 выстрелов. Определить: а) вероятность того, что будет ровно 45 промахов, б) наивероятнейшее число попаданий, в) вероятность того, что будет от 50 до 100 попаданий.



Контрольная работа № 6.

Дана выборка:

8, 7, 8, 7, 7, 7, 10, 8, 6, 7, 9, 7, 8, 8, 9, 8, 4, 8, 5, 9, 8, 10, 6, 7, 7, 8, 6, 5, 7, 11, 5, 4, 9, 6, 10, 5, 9.
  1. Найти статистическое распределение выборки.
  2. Построить полигон частот.
  3. Найти выборочное среднее.
  4. Найти выборочное среднеквадратичное отклонение и исправленное среднеквадратичное отклонение.
  5. Найти доверительные интервалы для генерального среднего и среднеквадратичного отклонения с надежностью γ = 0,95.



Контрольная работа № 7.

Найти уравнение линейной регрессии Y на X и определить тесноту связи.


х
0,10
1,00
1,50
1,70
2,00
2,50
3,00

у
5,00
4,00
4,00
3,00
2,50
3,00
1,80



8. Образовательные технологии.

    В процессе изучения дисциплины используются следующие образовательные технологии: традиционные лекции и практические занятия, интерактивные формы лекций и практических занятий: тренинги, занятия в малых группах, самостоятельная работа, плановые и дополнительные консультации.



9. Учебно-методическое и информационное обеспечение дисциплины (модуля).


Основная литература:
  1. Шипачёв В. С. Высшая математика. - М: Высшая школа, 2001. - 479 с.
  2. Высшая математика для экономистов. Под ред. Н.Ш.Кремера., М.,Юнити, 2004 – 471 с.
  3. Гмурман В. Е. Теория вероятностей и математическая статистика: Учебное пособие для студентов вузов. - М.: Высшая школа, 2001. - 400 с.
  4. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.,Юнити, 2001.
  5. Шипачёв В. С. Задачник по высшей математике.-М: Высшая школа, 2004 - 303 с.
  6. Данко П. Е., Попов А. Е., Кожевникова Т. Я. Высшая математика в упражнениях и
    задачах. Ч. 1. - М.: Высшая школа, 1999. - 304 с.
  7. Данко П. Е., Попов А. Е., Кожевникова Т. Я. Высшая математика в упражнениях и
    задачах. Ч. 2. - М.: Высшая школа, 1999. - 416 с.
  8. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высшая школа, 2001. - 400 с.



Дополнительная литература:
  1. Белько И.В, Кузьмич К.К. Высшая математика для экономистов. М. ООО «Новое Знание», 2002, ч. 1,2,3.
  2. Воронов М. В., Мещерякова Г. П. Математика для студентов гуманитарных факультетов. - Ростов-на-Дону: Феникс, 2002. - 384 с.
  3. Высшая математика / Под ред. Г. Н. Яковлева. - М.: Просвещение, 1988.
  4. Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики. - М.: Наука,
    1986.-576 с.
  5. Калинина В. Н., Панкин В. Ф. Математическая статистика. - М.: Высшая школа,
    1998.-336 с.
  6. Экономико-математические методы и прикладные модели / Под ред. В. В. Федосеева. - М.: ЮНИТИ, 2001. - 391 с.
  7. Белько И. В., Свирид Г. П. Теория вероятностей и математическая статистика. Примеры и задачи. - Минск: ООО «Новое знание», 2002. - 250 с.



10. Технические средства и материально-техническое обеспечение дисциплины.



    Мультимедийная аудитория, персональный компьютер, программное обеспечение.