Рабочая программа дисциплины «нелинейные уравнения математической физики» Рекомендовано

Вид материала

Рабочая программа

Содержание Ен.ф.03. нелинейные уравнения математической физики Цели и задачи учебной дисциплины Задачи изложения и изучения дисциплины Содержание теоретической части дисциплины Содержание практической части дисциплины Самостоятельная (внеаудиторная) работа (50 часов) Распределение часов курса по темам и видам работ Текущий и итоговый контроль Контрольные вопросы Учебно-методическое обеспечение дисциплины

Подобный материал:

• Учебно-методический комплекс по дисциплине Линейные и нелинейные уравнения физики (Методы, 325.5kb.
• М. К. Аммосова рабочая программа дисциплины «Уравнения математической физики» (специальность, 50.63kb.
• Учебно-методический комплекс по дисциплине опд. Ф. 02. Методы математической физики., 351.4kb.
• Уравнения математической физики направление подготовки, 18.02kb.
• Рабочая учебная программа дисциплины Уравнения математической физики Направление подготовки, 224.86kb.
• Учебно- методический комплекс по дисциплине опд. Ф 02. Методы математической физики, 340.98kb.
• Программа курса «уравнения математической физики» для математического отделения, 34.71kb.
• Программа дисциплины Уравнения математической физики для направления 010500. 62 «Прикладная, 204.13kb.
• Н. Г. Чернышевского кафедра теоретической и математической физики рабочая программа, 173.64kb.
• Содержание уравнения математической физики (нм-3) Уравнения математической физики (нп-3), 92.05kb.

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ


Утверждаю

Декан ____________факультета

«___»________________200___г.


РАБОЧАЯ ПРОГРАММА

ДИСЦИПЛИНЫ

«НЕЛИНЕЙНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ»

Рекомендовано

Методической комиссией

_______________факультета


председатель методической

комиссии

________________________

«___»_____________2005г.


Томск – 2005г.


Программа обсуждена и на заседании кафедры теоретической физики

________________________

(дата)


Заведующий кафедрой Шаповалов Александр Васильевич


УДК 501

ББК 22.31

С 60

Аннотация

ЕН.Ф.03. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

061800 (с)

Каф. ТФ ФФ

Проф., д.ф.-м.н. Шаповалов А.В.

Тел./факс: (3822)-529843

Цель: данный курс направлен на подготовку специалиста, владеющего современными представлениями о закономерностях, присущих нелинейным физическим явлениям, методами построения и исследования нелинейных уравнений, описывающих основные нелинейные процессы, формирование у студента целостного представления о сложных нелинейных процессах и явлениях на основе синергетического подхода и концепции самоорганизации.

Требования к разделам программы определяются государственным образовательным стандартом высшего профессионального образования к уровню подготовки выпускника по специальности 010701-физика, 010704 – физика конденсированного состояния вещества

Рабочая программа рассчитана на односеместровый курс изучения дисциплины. Практические занятия способствуют закреплению теоретических знаний и приобретению навыков решения конкретных задач.


Содержание: В курс включены разделы, составляющие основу современных представлений о нелинейных явлениях. К числу актуальных проблем относятся: анализ процессов распространения тепла в нелинейной среде, формирование диссипативных структур, нелинейные волны, солитонные явления.

Курс направлен на приобретение студентом теоретических знаний и практических навыков в области физики нелинейных явлений.


Курс 3 ( 6 сем – зачет, экзамен).

Всего 50 ч, в т. ч.: Лк 30 ч, , Пр 16 ч,

Цели и задачи учебной дисциплины

Цели преподавания дисциплины

Целью курса является подготовка специалиста, владеющего современными представлениями о закономерностях, присущих нелинейным, методами построения и исследования моделей нелинейных систем, формирование у студента целостного представления о сложных процессах и явлениях на основе синергетического подхода и концепции самоорганизации. Требования к разделам программы определяются государственным образовательным стандартом высшего профессионального образования к уровню подготовки выпускника по специальности 010701-физика, 010704 – физика конденсированного состояния .

Рабочая программа рассчитана на односеместровый курс изучения дисциплины. Практические занятия способствуют закреплению теоретических знаний и приобретению навыков решения конкретных задач. В результате изучения курса студент должен иметь представление:

• об особенностях, присущих нелинейным системам, о классах нелинейных уравнений, об отличиях нелинейных систем от линейных,
  
• о математических методах и моделях, описывающих нелинейные системы, о широкой области применения нелинейных моделей,
  
• об общности понятий и представлений, используемых в нелинейной математической физике, их применимости к анализу сложных систем и процессов, взаимосвязи с другими математическими и физическими дисциплинами;
  

уметь:

• выделять в конкретных физических, технических и других проблемах задачи, допускающие формулировку и решение методами нелинейной математической физики.
  

Задачи изложения и изучения дисциплины

В результате лекционных, практических и самостоятельных занятий в рамках предложенной программы студент должен:

• знать примеры нелинейных систем и явлений и иметь представление об особенностях, отличающих нелинейные системы от линейных;
  
• знать основные виды нелинейных уравнений, описывающих различные явлений,
  
• иметь представление о закономерностях нелинейного распространения тепла, включая режим с обострением;
  
• усвоить основные представления о нелинейных волнах;
  
• иметь представления о солитонных уравнениях и методе обратной задачи рассеяния.
  

Содержание теоретической части дисциплины

СЕМЕСТР VI (34 часа)

Тема I. Классы квазилинейных уравнений (4 часа)

1. Нелинейные системы и их модели.
   
2. Особенности нелинейных систем. Классификация квазилинейных уравнений.
   
3. Метод приведения квазилинейного уравнения второго порядка к каноническому виду.
   
4. Канонический вид квазилинейного уравнения второго порядка.
   

Тема II. Распространение тепла в нелинейной среде. (6 часов)


2.1. Физические закономерности распространения тепла. Закон Фурье.

2.2. Отклонение от линейного закона теплопроводности.

2.3. Нелинейное уравнение теплопроводности. Задачи с внешней и внутренней нелинейностью.

2.4. Свойства автомодельности. Автомодельные переменные и автомодельные решения нелинейных уравнений. Распространение тепла в среде с фазовым переходом. Задача Стефана о фазовом переходе.

2.5. Распространение теплового возмущения в нелинейной среде. Распространение тепла от мгновенного теплового источника. Автомодельное решение нелинейного уравнения теплопроводности.

2.6. Понятие о тепловой волне. Пространственная локализация теплового возмущения.

2.7. Понятие о режимах с обострением.


Тема III. Системы типа «реакция-диффузия». (4 часа)

3.1. Распределенные системы с обратной связью. Положительная и отрицательная обратная связь. Понятие об активаторе и ингибиторе.

3.2. Диссипативные структуры и самоорганизация в активных средах.

3.3. Модель двухкомпонентной системы типа «реакция - диффузия», с активатором и –ингибитором.

3.4. Стационарное состояние и его устойчивость.

3.5. Критерии устойчивости стационарного состояния в двухкомпонентной системе.

3.6. Обзор известных моделей типа «реакция - диффузия». Модель Гирера-Майнхарда. Модель «брюсселятор».


Тема IV. Нелинейные волны. (4 часа)


4.1. Волновые движения и их классы. Гиперболические волны.

4.2. Волны в среде с дисперсией.

4.3. Распространение волны в нелинейной среде. Эффект опрокидывания фронта.

4.4. Волновое уравнение первого порядка. Решение уравнения методом характеристик. Понятие об ударной волне. Слабые ударные волны.


Тема V. Обратная задача рассеяния. (6 часов)


5.1. Обратная задача рассеяния в квантовой механике. Задача рассеяния для одномерного уравнения Шредингера. Непрерывный спектр.

5.2. Аналитические свойства матрицы переноса.

5.3. Функции Иоста и их свойства.

5.4. Дискретный спектр в задаче рассеяния.

5.5. Понятие о данных рассеяния. Уравнения Гельфанда-Левитана-Марченко и решение обратной задачи рассеяния. Формула для потенциала.


Тема VI. Интегрирование нелинейных уравнений методом обратной задачи. (6часов)


6.1. Понятие об (L-A) –паре Лакса для нелинейного уравнения. Свойства нелинейного уравнения, обладающего (L-A) –парой.

6.2. Пара Лакса для уравнения Кортевега – де Фриза. Эволюция данных рассеяния.

6.3. Схема метода обратной задачи рассеяния для интегрирования нелинейного уравнения Кортевега – де Фриза.


Тема VII. Солитонные решения. (4часа)


7.1. Безотражательные потенциалы и солитонные решения.

7.2. Общий вид N-солитонного решения уравнения Кортевега - де Фриза.

7.3 Односолитонное решение и его свойства.

Содержание практической части дисциплины

СЕМЕСТР VI (16 часаов)

1. Решение задач по теме: Классификация квазилинейных уравнений II порядка. (2 часа).
   
2. Решение задач по теме: Нелинейные процессы теплопроводности. (4часа).
   
3. Решение задач по теме: Системы типа «реакция-диффузия» (2 часа).
   
4. Решение задач по теме: Нелинейные волны. Явление опрокидывания фронта волны (2 часа).
   
5. Решение задач по теме: Задача рассеяния в квантовой механике и нелинейные уравнения (2 часа).
   
6. Решение задач по теме:Нелинейные уравнения, обладающие (L-A)-парой и их свойства (2часа).
   
7. Решение задач по теме: Задача рассеяния в квантовой механике и нелинейные уравнения (2 часа).
   

Самостоятельная (внеаудиторная) работа (50 часов)

Самостоятельная внеаудиторная работа включает в себя: изучение теоретического материала: разделов теории нелинейного распространения тепла с переносом массы, с нелинейными источниками (10 часов), свойств нелинейных волн (6 часов), изучение свойств моделей систем типа «реакция-диффузия» (10 часов), изучение солитонных уравнений, интегрируемых методом обратной задачи рассеяния (10 часов), построение и исследование солитонных решений этих уравнений (14 часов).


Распределение часов курса по темам и видам работ

№ п/п	Наименование тем	Всего часов	Аудиторные занятия (час) В том числе			Самостоятельная работа
			Лекции	Семинары	Лабораторные занятия
1	Тема I	16	4	2		10
2	Тема II	16	6	4		6
3	Тема III	16	4	2		10
4	Тема IV	16	4	2		10
5	Тема V	22	6	2		14
6	Тема VI	8	6	2
7	Тема VII6	6	4	2
Итого		100	34	16		50

Текущий и итоговый контроль

Текущий контроль изучения курса студентами осуществляется по итогам выполнения контрольных заданий, результатам аудиторной работы студента в соответствии с графиком текущего контроля.

Тема	Отчетность	Срок (неделя)
Классификация нелинейных уравнений и систем	Индивидуальное задание 1	5
Нелинейные процессы теплопроводности. Системы типа «реакция-диффузия»	Контрольная работа 2	7
Обратная задача рассеяния для 1-мерного уравнения Шредингера. Солитонные решения	Контрольная работа 3	14
	Зачет	16

Итоговым контролем является семестровый зачет по практическим занятиям и экзамен. Зачет проставляется по результатам текущего контроля, при условии успешного выполнения, контрольных работ, аудиторного текущего контроля.

Контрольные вопросы

1. Классификация квазилинейного уравнения II порядка с двумя независимыми переменными. Формулы преобразования коэффициентов при вторых производных. Типы уравнения II порядка.
   
2. Записать систему уравнений, определяющих переход к канонической форме квазилинейного уравнения II порядка, если коэффициенты при вторых производных зависят от искомой функции. В чем отличие от случая линейного уравнения?
   
3. Получить формулу для коэффициента 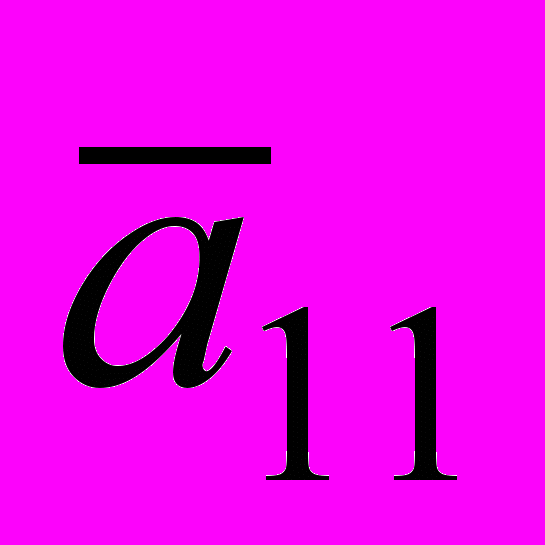в канонических переменных.
   
4. Получить условие Стефана на границе раздела твердой и жидкой фаз.
   
5. Сформулировать задачу Стефана о фазовом переходе.
   
6. Построить автомодельное решение в задаче Стефана.
   
7. Найти уравнение движения фронта раздела фаз в задаче Стефана.
   
8. Задачи с внутренней нелинейностью. Задача о распространении тепла в среде с коэффициентом теплопроводности, степенным образом зависящим от температуры.
   
9. Получить уравнение движения фронта тепловой волны в среде со степенной зависимостью коэффициента теплопроводности от температуры.
   
10. Показать, что в среде с нелинейным коэффициентом теплопроводности в пределе решение нелинейного уравнения теплопроводности переходит в решение линейной задачи.
    
11. Система уравнений типа «реакция-диффузия ». Понятие об активаторе и ингибиторе. Постановка задачи об образовании диссипативных структур.
    
12. Получить условия нарушения устойчивости в задаче типа «реакция- диффузия».
    
13. Получить условия неустойчивости для осциллирующих флуктуаций. При каком условии в среде всегда возникает осциллирующие во времени флуктуации?
    
14. Условия возникновения апериодических во времени флуктуаций.
    
15. Найти стационарное решение и условия неустойчивости в модели Гирера- Майнхарда.
    
16. Найти стационарное решение в модели брюсселятора. Найти критическое значение управляющего параметра и малого параметра.
    
17. Дать определение гиперболической и диспергирующей волн.
    
18. Найти решение уравнения методом характеристик.
    
19. Объяснить явление опрокидывания фронта волны, распространяющеся в нелинейной среде. Записать условие опрокидывания фронта волны.
    
20. Сформулировать постановку задачи о рассеянии на потенциале для одномерного квантовомеханического уравнения Шредингера.
    
21. Объяснить квантовомеханический смысл функций , в задаче рассеяния. Доказать соотношение , .
    
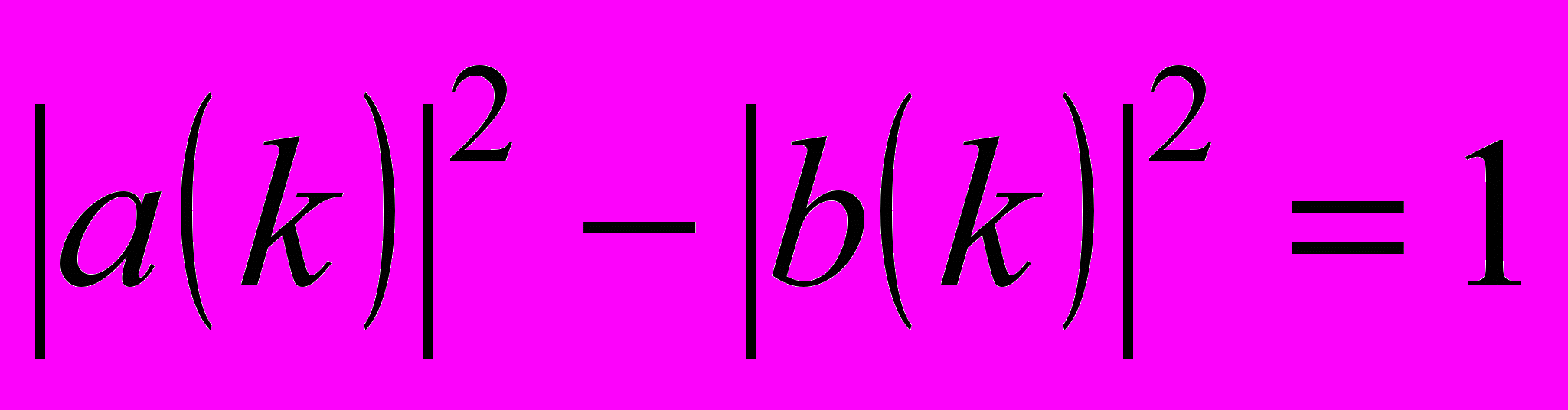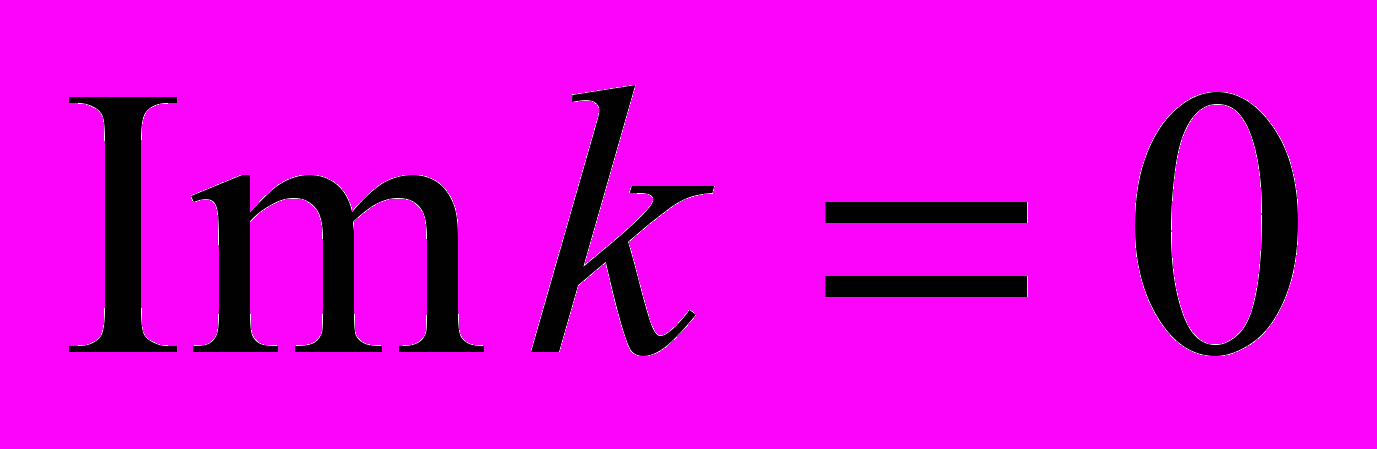22. Вычислить вронскиан функций Иоста .
    
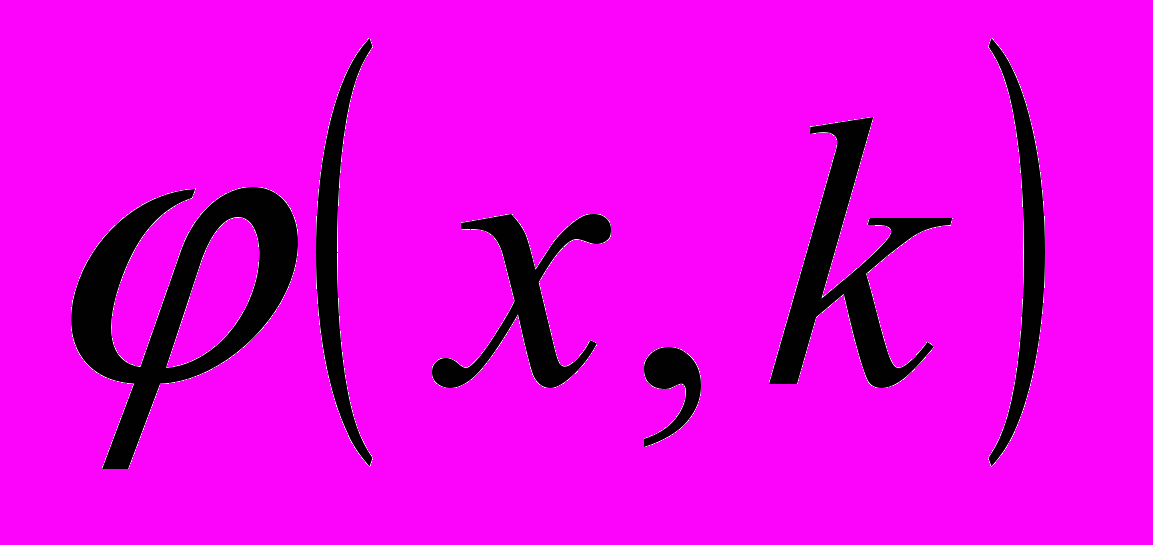
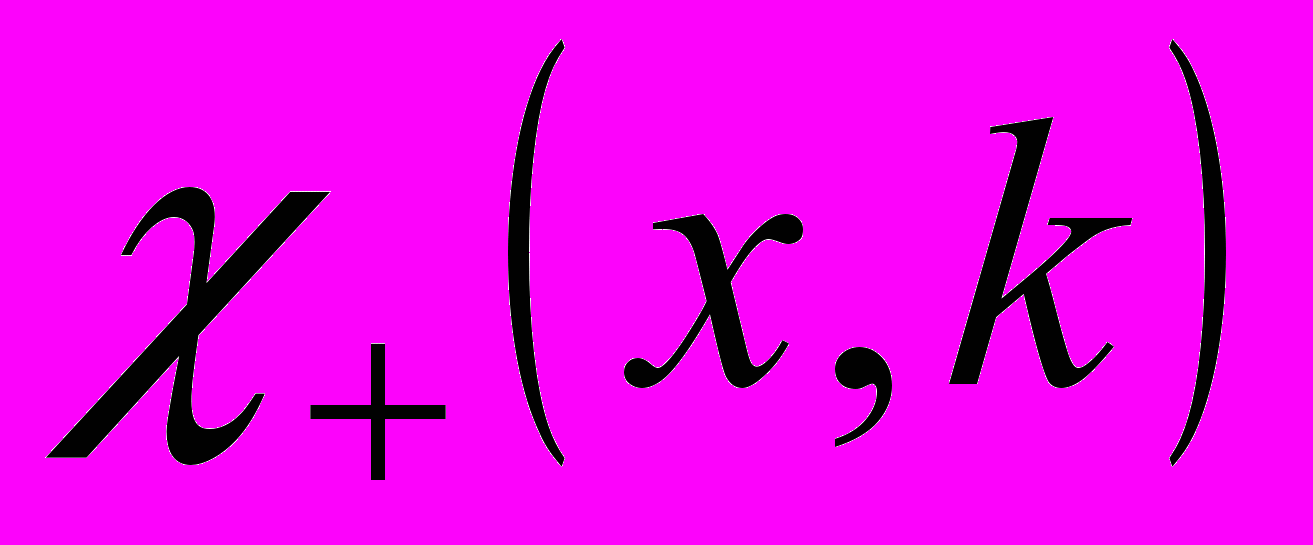23. Записать интегральное уравнение, определяющее функцию Иоста и показать, что аналитична в верхней полуплоскости .
    
24. Доказать, что точки верхней полуплоскости , в которых обращается в нуль, являются точками дискретного спектра для одномерного уравнения Шредингера .
    
25. Сформулировать постановку обратной задачи рассеяния для одномерного уравнения Шредингера в квантовой механике.
    
26. Понятие о данных рассеяния. Вывод уравнений Гельфанда-Левитана-Марченко.
    
27. Получить формулу, выражающую потенциал 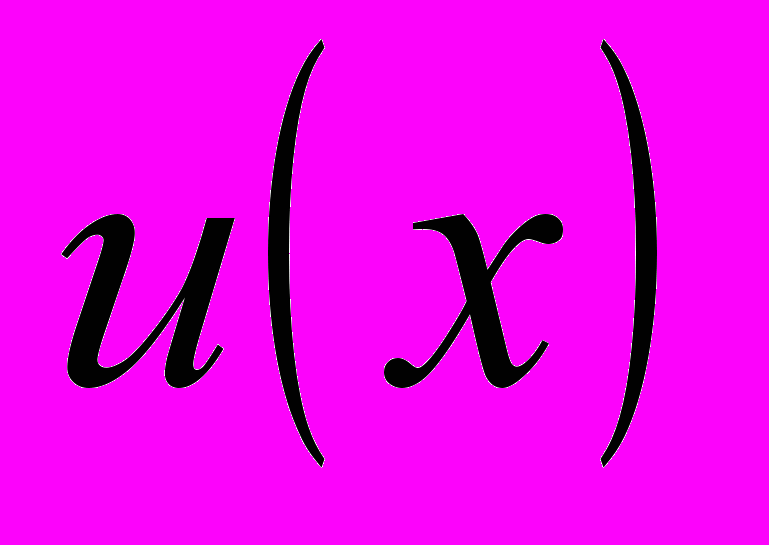в обратной задаче рассеяния. Уравнение Кортевега-де Фриза (КдФ).
    
28. Понятие об (L-A)-паре для нелинейного уравнения. (L-A)-пара для уравнения КдФ.
    
29. Показать, что если удовлетворяет уравнению КдФ, то дискретные собственные значения уравнения Шредингера 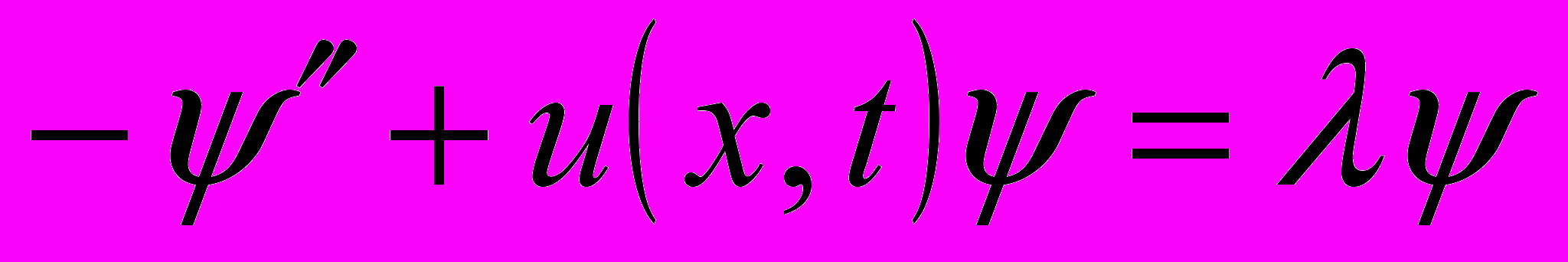не зависят от .
    
30. Понятие от эволюции данных рассеяния для потенциала , удовлетворяющего уравнению КдФ. Уравнения Гарднера-Грина-Крускала-Миуры.
    
31. Схема интегрирования уравнения КдФ методом обратной задачи рассеяния.
    
32. Понятие о безотражательном потенциале в обратной задаче рассеяния. Решения уравнений Гельфанда-Левитана-Марченко для безотражательного потенциала.
    
33. N-солитонное решение уравнения КдФ. 1-солитонное решение.
    

Учебно-методическое обеспечение дисциплины

Перечень рекомендуемой литературы на русском языке

1. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Изд-во МГУ, 1999.
   
2. Мартинсон Л.К., Малов Ю.И. Дифференциальные уравнения математической физики. М.: Изд-во МГТУ им. Н.Э. Баумана, 1996.
   
3. Курант Р. Уравнения с частными производными. М.: Мир, 1964.
   
4. Математическое моделирование. Нелинейные дифференциальные уравнения математической физики./ Ред. Акад. А.А. Самарский, чл.-корр. С.П. Курдюмов, В.И. Мажукин. М.: Наука, 1987.
   
5. Режимы собострением. Эволюция идеи: Зоконы коэволюции сложных структур. М.: Наука, 1998.
   
6. Кернер Б.С., Осипов В.В. Самоорганизация в активных распределенных средах. // Успехи физических наук. 1990. Т.160. Вып. 9. С.1-73.
   
7. Уизем Дж. Линейные и нелинейные волны. М.: Мир, 1977.
   
8. Захаров В.Е., Манаков С.В., Новиков С.П., Питаевский Л.П. Теория солитонов: Метод обратной задачи. М.: Наука, 1980.
   
9. .Тахтаджян Л.А., Фаддеев Л.Д. Гамильтонов подход в теории солитонов. М.,: Наука1986.
   
10. .Абловиц М., Сигур Х. Солитоны и метод обратной задачи. М.: Мир, 1987
    
11. Додд Р., Эйлбек Дж., Гиббон Дж., Моррис Х. Солитоны и нелинейные волновые уравнения. М.: Мир, 1988.
    
12. .Ньюэлл А. Солитоны в математике и физике. М.: Мир, 1989.
    
13. .Калоджеро Ф., Дегасперис А. Спектральные преобразования и солитоны. М.: Мир, 1985.
    
14. Марченко В.А. Операторы Штурма-Лиувилля и их приложения. Киев: Наукова Думка, 1977.
    
15. Левитан Б.М. Обратные задачи Штурма-Лиувилля. М.: Наука, 1984.
    
16. Альперин М.М., Клубис Я.Д., Хижняк А.И. Введение в физику двухуровневых систем. Киев: Наукова Думка, 1987.
    

Англоязычная литература


Courant R. Methods of mathematical physics. Vol. II. Partial differential equations, Interscience, London, 1962.

Whitham C.B. Linear and nonlinear waves, Wiley, Interscience, New York, 1974.

Landau L.D. and Lifshitz E.M. Fluid mechanics, Pergamon Press, London, 1989.

Haken H. Synergetics, Berlin, Springer, 1978.

Haken H. Advanced synergetics. Instability hierarchies of self-organizing systems and devices, Berlin, Heidelberg, Springer-Verlag, 1993.

Kurdyumov S.P., Malinetskii G.G., and Potapov A.B. Nonstationary structures, dynamic chaos, and sellular automata. Int. J. Fluid Mech. Research, 1996. Vol/22.N. 5-6.P.75-133.

Zakharov V.E., Manakov S.V., Novikov S.P., and Pitaevsky L.P. Theory of Solitons: The Inverse Scattering Method, Nauka, Moscow, 1980 [English transl.: Consultants Bureme, New York, 1984].

Ablovitz M. And Segur H. Solitons and the Inverse Scattering Transform, SIAM, Philadelphia, 1981.

Dodd R.K., Eilbeck J.C., Gibbon J.D., and Morris H.C. Solitons and Nonlinear Wave Equations, New York, London, Toronto, Montreal, Sydney, Tokyo, Academic Press, 1982.

Newell A. Solitons in Mathematics and Physics, SIAM, Philadelphia, 1985.

Calogero F., Degasperis A. Spectral transform and solitons. Vol. I. Tools to solve and investigate nonlinear evolution equations, North-Holland, Amsterdam and Ney York, 1982.

Faddeev L.B and Takhtatjan l.A. Hamiltonian methods in the theory of silitons, Springer-Verlag, 1987.

Solitons – Bullough R.K., Caudrey P.J., Editors – Springer-Verlag, Berlin, Heidelberg, New York, 1980.

Karpman V.I. Nonlinear waves in dispersive media, Pergamon Press, Ney York, 1975.

Naumkin P.I., Shishmarev I.A. Nonlinear nonlocal equations in the theory of waves,

American Mathematical Society, Providence , Rhode Island, 1994.

Vasilev V., A., Romanovskii Yu.M., Chernavskii D.S., Yakhno V.G. Autowave processes in kinetic systems, Berlin, 1986.

Ames W.F. Nonlinear partial differential equations in engineering. Vol 2. Academic Press, New York, 1972.

Differential Equations and Mathematical Physics - Weikard R., and Weinstein G., Editors - American Mathematical Society, Providence , Rhode Island, 2000


Mathematics of Nonlinear Science - Melvyn S. Berger, Editor - American Mathematical Society, Providence , Rhode Island, 1990.

Strauss W.A. Nonlinear Wave Equations, American Mathematical Society, Providence , Rhode Island, 1989

Hasegawa A., Optical solitons in fibers, Springer, Heidelberg, 1989.

Hasegawa A. and Kodama Y., Solitons in optical communications, Oxford University Press, Oxford, 1996.


ПРИЛОЖЕНИЕ 1

Темы для рефератов


1 Распространение тепла в нелинейной среде с учетом релаксации теплового потока.

Литература:

1)Тихонов А.Н., Самарский А.А. Уравнения математической физики. Учеб. пособие. --- 6-е изд., испр. и доп. М.: Изд-во МГУ, 1999. - 798 с.

2) Математическое моделирование. Нелинейные дифференциальные уравнения математической физики./Отв. ред. Акад. А.А. Самарский, чл.-корр. АН РАН С.П. Курдюмов, к.ф.-м.н. В.И. Мажукин. М.: Наука, 1987. – 280 с.

3) Мартинсон Л.К., Малов Ю.И. Дифференциальные уравнения математической физики. М.:Изд-во МГТУ им. Н.Э. Баумана, 1966.- 367 с.

4) Уизем Дж. Линейные и нелинейные волны. М.: Мир, 1977. – 622 с.

2) Нелинейные волны в диспергирующей среде.

Литература:

1)Ньюэлл А. Солитоны в математике и физике. М.: Мир, 1989. – 323 с.

2)Абловиц М., Сигур Х. Солитоны и метод обратной задачи. М.: Мир, 1987. – 480 с.

3) Додд Р., Эйлбек Дж., Гиббон Дж., Моррис Х. Солитоны и нелинейные волновые уравнения. - М.: Наука, 1988. 694 с.

5) Soliton theory and its applications./Ed . Gu Chaohao. Berlin, Heidelberg, Toronto, London, Paris, Tokio: - Springer, 1991 403 pp.


6) Солитоны/ Ред. Буллаф Р., Кодри Ф./пер.с англ. Дубровина Б.А., Кричевера И.М., Манакова С.В. Под. Ред. С.П. Новикова. М.: Мир, 1983. 408 с.

3) Односолитонное решение нелинейного уравнения Шредингера.

Литература:

1)Ньюэлл А. Солитоны в математике и физике. М.: Мир, 1989. – 323 с.

2)Абловиц М., Сигур Х. Солитоны и метод обратной задачи. М.: Мир, 1987. – 480 с.

3) Захаров В.Е., Манаков С.В., Новиков С.П., Питаевский Л.П. Теория солитонов: Метод обратной задачи. - М.: Наука, 1980. 319 с.

4) Додд Р., Эйлбек Дж., Гиббон Дж., Моррис Х. Солитоны и нелинейные волновые уравнения. - М.: Наука, 1988. 694 с.

5) Солитоны/ Ред. Буллаф Р., Кодри Ф./пер.с англ. Дубровина Б.А., Кричевера И.М., Манакова С.В. Под. Ред. С.П. Новикова. М.: Мир, 1983. 408 с.

6) Калоджеро Ф., Дегасперис А. Спектральные преобразования и солитоны. Методы решения и исследования эволюционных уравнений. - М.: Наука, 1988. 469 с.

7) Тахтаджян Л.А., Фаддеев Л.Д. Гамильтонов подход в теории солитонов. М.: Наука, 1986. 327 с.


ПРИЛОЖЕНИЕ 2 Примеры контрольных работ


Тест-контрольная работа 1.