Geum.ru

Содержание

Вид материалаДокументы

Содержание


4.5. Алгоритм улучшения плана
Вторая итерация Этап 1
Подобный материал:
1   ...   9   10   11   12   13   14   15   16   17

4.5. Алгоритм улучшения плана


Сформулируем теперь алгоритм перехода к новому опорному плану, дающему меньшее значение функции потерь. Прежде, чем формулировать его в общем виде, покажем его основные моменты на том примере, который мы начали рассматривать.

Вспомним, что ограничения двойственной задачи соответствовали тому, что 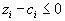, а выполнение условия 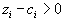говорило о том, что соответствующий вектор надо вводить в базис. Поэтому и выполнение

условия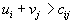

говорит о том, что вектор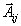

надо вводить в базис.

У нас условие 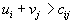выполнено в двух случаях  для 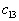и 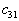. Вообще

принято вводить в базис тот вектор, для которого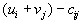




максимально. В данном случае это вектор ,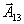

но в учебных целях мы




введем в базис вектор .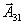

Введение в базис вектора 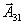означает, что мы должны запланировать какую-то перевозку из третьего склада в первый пункт потребления. Пусть величина этой перевозки равна  . Поставим ее в клетку, соответствующую i =3, j =1. Тогда мы получим следующий план перевозок:



2
3.1

 
 



3.9

4.2

 





 
2.8

6.3


Но теперь у нас нарушился баланс запасов и потребностей  получилось, что

из третьего склада вывозится ,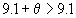
а в первый пункт потребления




 поступает .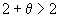
 

Необходимо восстановить баланс запасов и потребностей. Для этого поступают следующим образом: по ненулевым компонентам плана перевозок (включая и компоненту  ) строят цикл вида столбец  строка столбец строка ... строка (см. рисунок), который начинается и кончается на компоненте  .

Теперь для восстановления баланса запасов и потребностей можно поступить очень просто: при движении по столбцу от имеющихся компонентов плана надо отнимать  , а при движении по строке  наоборот, прибавлять  . В результате получится следующий план перевозок, уже сохраняющий баланс запасов и потребностей:

2-

3.1+

 
 

 
3.9-

4.2+

 



 
2.8-

6.3

С балансом всё в порядке, но теперь у нас стало 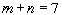компонент плана, а должно быть 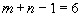. Поэтому надо выбрать  так, чтобы одна из бывших компонент обратилась в нуль, но все остальные компоненты остались положительными. Легко догадаться, что для этого  надо взять равным минимальному из тех чисел, из которых  вычитается. В нашем случае  вычитается из чисел 2; 3.9; 2.8 . Минимальное из них есть 2 и поэтому надо взять  =2.

В результате получится новый опорный план следующего вида

 
5.1

 
 

 
1.9

6.2

 

2

 
0.8

6.3




в котором снова будет положенные ему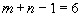

компонент.

Вычисляя транспортные расходы для этого плана, мы получим 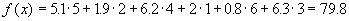, откуда видно, что по сравнению с исходным планом транспортные расходы уменьшились на 2 единицы.

Опишем этот процесс в общем виде.

Итак, пусть для некоторой пары индексов 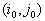выполнено условие 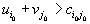. Тогда вектор 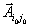надо вводить в базис. Если таких векторов окажется несколько, то обычно вводят в базис тот вектор, для которого

величина разности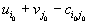

максимальна.

Исходя из клетки 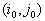строят цикл по ненулевым компонентам плана перевозок по маршруту столбец  строка  столбец  строка  ...  строка, который начинается и заканчивается в клетке 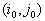. Мы не будем доказывать следующие два утверждения:

 такой цикл всегда может быть построен;

 такой цикл единственный.

Итак, пусть этот цикл имеет вид



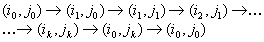
Установим новый план перевозок вида



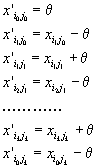
Все остальные компоненты плана перевозок, не входящие в цикл, остаются неизменными.

Наконец, выберем  таким образом, чтобы одна из новых компонент плана обратилась в нуль, а все остальные остались положительными. Для этого  следует взять в виде ,

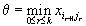где считается .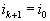
 

В результате получится новый опорный план. Покажем, что этот новый опорный план дает меньшее значение транспортных расходов, чем старый план.

Так как компоненты плана, не входящие в цикл, не изменяются, то их можно не учитывать. Для ненулевых компонент исходного плана

выполнялось условие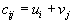

и поэтому







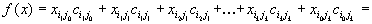
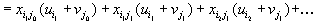
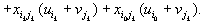
Для нового плана перевозок мы имеем




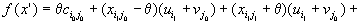
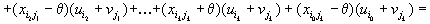
В выражении, стоящем в квадратных скобках, большинство слагаемых сокращается и окончательно получаем



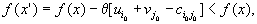
так как мы вводим перевозку, для которой .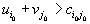
 

Ну, а дальнейшее очевидно: надо повторять все итерации до тех пор, пока не будет получен оптимальный план. В силу конечности числа вершин допустимой области, это может быть сделано за конечное число шагов.

Закончим наш учебный пример. Одну итерацию мы уже проделали.

Вторая итерация
Этап 1

Определение потенциалов и проверка оптимальности плана. Обычно это совмещается в одной таблице и выглядит в виде таблицы, приведенной на следующей странице.

Сначала в таблицу выписываются 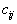, соответствующие ненулевым компонентам плана. Для наглядности их можно как-то помечать, скажем, обводить рамкой (в книге они отмечены жирным шрифтом).

 
2

5

7

4



0
2

5

7

4



-3
-1

2

4

1

-1

1

4

6

3

Затем определяются потенциалы. Обычно это легко сделать в уме, двигаясь по строкам и столбцам.

Затем оставшиеся клетки заполняются суммами соответствующих

потенциалов, то есть величинами .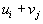

 

Наконец, производится сравнение получившейся таблицы с таблицей

величин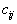

и определяются те клетки, где .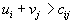

 

Этап 2

Из тех пар индексов, где 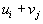, находится та пара, где разность 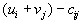максимальна (в нашем случае это пара i =1, j =3). Строится цикл, определяется  и строится новый опорный план.

В нашем случае эти преобразования имеют следующий вид:
5.1-



 
 
 
 
5.1

 



1.9+

6.2-

 


 
7

1.1

 

2

 
0.8

6.3

 
2

 
0.8

6.3


В нашем случае 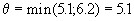, так что новый опорный план нарисован в таблице справа. Значение транспортных расходов уменьшилось на величину

,

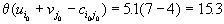то есть на 15.3 единицы.

Следующая итерация дается без пояснений.

Третья итерация
Этап 1

 
-1

2

4

1

0

-1

2

4

1

0

-1

2

4

1

2

1

4

6

3

В данном случае для всех клеток таблицы выполняется условие 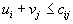, что говорит о том, что план перевозок, полученный на предыдущей итерации, является оптимальным.

Для этого плана перевозок значение транспортных расходов

.

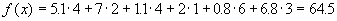По сравнению с исходным планом, полученным методом северо-западного угла, транспортные расходы уменьшились на 17.3 единицы, то есть на 21%.

Теперь мы в состоянии доказать одну интересную теорему

Теорема Если все запасы 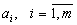и все потребности 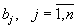целые числа, то оптимальный план перевозок тоже целочисленный.

Доказательство

Действительно, вспомните, как строился исходный опорный план методом северо-западного угла. При этом применялась только одна арифметическая операция  операция вычитания. А при вычитании целых чисел всегда получаются только целые числа. Поэтому исходный опорный план целочисленный.

При переходе к новому опорному плану применялись три операции: нахождение минимума из нескольких чисел (при определении  ), вычитание и сложение. В применении к целым числам эти операции всегда дают целые числа. Поэтому на любой итерации получающийся план является целочисленным, в том числе и оптимальный план. Теорема доказана.