Содержание
| Вид материала | Документы |
Содержание4.4. Методы проверки опорного плана на оптимальность Таблица стоимостей перевозок |
- Содержание дисциплины наименование тем, их содержание, объем в часах лекционных занятий, 200.99kb.
- Содержание рабочей программы Содержание обучения по профессиональному модулю (ПМ) Наименование, 139.63kb.
- Заключительный отчет июль 2010 содержание содержание 1 список аббревиатур 3 введение, 6029.85kb.
- 5. Содержание родительского правоотношения Содержание правоотношения, 110.97kb.
- Содержание введение, 1420.36kb.
- Сборник статей Содержание, 1251.1kb.
- Сборник статей Содержание, 1248.25kb.
- Анонсы ведущих периодических изданий содержание выпуска, 806.18kb.
- Вопросы к экзамену по дисциплине «Коммерческая деятельность», 28.08kb.
- Конспект лекций содержание содержание 3 налог на прибыль организаций 5 Плательщики, 795.2kb.
4.4. Методы проверки опорного плана на оптимальность
4.4.1. Потенциалы. Критерий оптимальности плана
Итак, наша транспортная задача имеет вид:
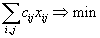
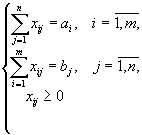
Распишем нашу задачу в векторной форме. Для этого введем векторы
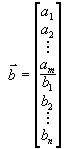
Тогда ограничения задачи (3) могут быть записаны в виде
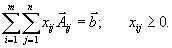
Как уже говорилось выше, одно из этих ограничений является лишним, и оно может быть вычеркнуто.
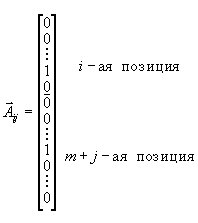
Рассмотрим теперь двойственную задачу. Так как ограничений всего m + n, то и соответствующие переменные двойственной задачи обозначим так:
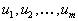 (переменные, соответствующие первым m ограничениям) и
(переменные, соответствующие первым m ограничениям) и 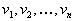 (переменные, соответствующие последним n ограничениям). Тогда, учитывая вид векторов
(переменные, соответствующие последним n ограничениям). Тогда, учитывая вид векторов 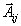 и вид вектора
и вид вектора 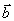 , запишем двойственную задачу в следующем виде:
, запишем двойственную задачу в следующем виде: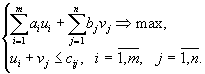
Величины
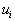 называются потенциалами складов, а величины
называются потенциалами складов, а величины 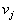 потенциалами пунктов потребления.
потенциалами пунктов потребления.Так как одно из ограничений является лишним, то на самом деле одного из потенциалов нет. Для сохранения симметрии всех формул и обозначений
| можно просто полагать, скажем, 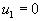 . . | |
Пусть теперь
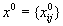 оптимальный опорный план транспортной задачи. Тогда, согласно теореме двойственности, должно выполняться условие
оптимальный опорный план транспортной задачи. Тогда, согласно теореме двойственности, должно выполняться условие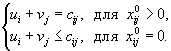
Это и позволяет проверить оптимальность любого опорного плана.
Сам алгоритм выглядит следующим образом:
- Один из потенциалов задается произвольно, скажем, полагается
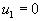 .
.
- Рассматривается система линейных уравнений вида
 для тех наборов индексов i , j , для которых
для тех наборов индексов i , j , для которых 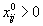 , и находятся потенциалы
, и находятся потенциалы 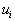 и
и 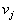 всех складов и всех пунктов потребления.
всех складов и всех пунктов потребления.
- Для всех остальных наборов индексов i , j (для которых
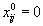 ) проверяется условие
) проверяется условие
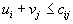 .
.Если это условие выполняется для всех наборов индексов i , j , для которых
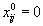 , то рассматриваемый план является оптимальным. Если же, хотя бы
, то рассматриваемый план является оптимальным. Если же, хотя бы| для одной пары 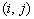 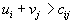 , , | то план не оптимален. |
Прежде, чем приводить пример, расскажем о том, как реализуется пункт 2 этого алгоритма, когда находятся потенциалы
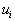 и
и 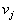 . Обычно он реализуется следующим образом:
. Обычно он реализуется следующим образом:1. Одна из величин
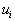 или
или 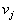 задается произвольно, например, полагается
задается произвольно, например, полагается 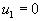 .
.2. Затем рассматриваются уравнения вида
 для тех j , для которых
для тех j , для которых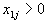 . Так как
. Так как 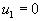 известно, то находятся
известно, то находятся 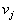 для некоторого множества индексов
для некоторого множества индексов 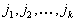
3. Для этих индексов
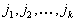 рассматриваются уравнения вида:
рассматриваются уравнения вида: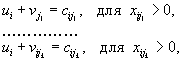
для тех
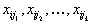 , которые больше нуля. Так как
, которые больше нуля. Так как 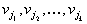 известны, тот находятся величины
известны, тот находятся величины 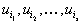 для некоторого множества индексов
для некоторого множества индексов 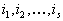 .
.4. Далее повторяются пункты 2 (движение по строкам) и 3 (движение по столбцам), пока не определятся все потенциалы.
Проиллюстрируем этот процесс примером, а заодно покажем форму записи результатов при ручном счете.
Пример
Пусть имеется три склада с запасами
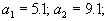
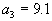 и четыре пункта потребления с потребностями
и четыре пункта потребления с потребностями 
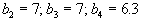 . Коэффициенты
. Коэффициенты 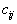 , определяющие стоимость перевозок, заданы матрицей:
, определяющие стоимость перевозок, заданы матрицей:Таблица стоимостей перевозок
| | Пункты потребления | |||
| Ск | 3 | 5 | 4 | 5 |
| ла | 1 | 2 | 4 | 3 |
| ды | 1 | 5 | 6 | 3 |
Построим исходный опорный план методом северо-западного угла. Он имеет вид
| 2 | 3.1 | 0 | 0 |
| 0 | 3.9 | 4.2 | 0 |
| 0 | 0 | 2.8 | 6.3 |
План имеет 6=3+4-1 компонент, поэтому он является невырожденным. Заметим, что для него транспортные расходы равны
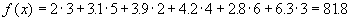 .
.Заготовим матрицу размером
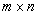 (в нашем случае размером 3 4), в которую впишем те коэффициенты
(в нашем случае размером 3 4), в которую впишем те коэффициенты 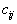 , которые соответствуют ненулевым перевозкам нашего плана (смотрите следующую страницу).
, которые соответствуют ненулевым перевозкам нашего плана (смотрите следующую страницу).Далее действуем следующим образом:
-
Полагаем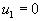 .
.
-
| | 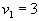 |  | 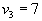 | 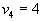 |
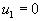 | 3 | 5 | | |
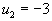 | | 2 | 4 | |
 | | | 6 | 3 |
- Идем по строке.
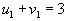 , следовательно
, следовательно 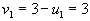 ;
;
-
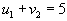 , следовательно , следовательно 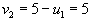 . . |
- Идем по столбцу.
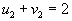 , следовательно
, следовательно 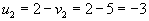 .
.
- Идем по строке.
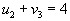 , следовательно
, следовательно 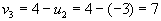 .
.
- Идем по столбцу.
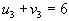 , следовательно
, следовательно  .
.
- Идем по строке.
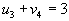 , следовательно , следовательно 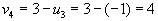 . . |
Таким образом, определились потенциалы всех пунктов и складов и пунктов потребления. Теперь можно закончить заполнение этой таблицы, вписав в пустые клетки суммы
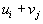 , то есть суммы соответствующих потенциалов. В результате получим:
, то есть суммы соответствующих потенциалов. В результате получим:| | 3 | 5 | 7 | 4 |
| 0 | 3 | 5 | 7 | 4 |
| -3 | 0 | 2 | 4 | 1 |
| | 2 | 4 | 6 | 3 |
В ней жирным шрифтом помечены те
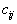 , которые использовались для нахождения потенциалов.
, которые использовались для нахождения потенциалов.Сравнивая с матрицей величин,
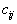 мы видим, что условие оптимальности плана
мы видим, что условие оптимальности плана 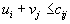 нарушено в двух местах для
нарушено в двух местах для 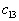 и
и 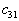 . Следовательно, построенный нами план перевозок не является оптимальным.
. Следовательно, построенный нами план перевозок не является оптимальным.4.4.2. Дельта-метод
Рассмотрим алгоритм дельта-метода в общем виде:
- Рассмотрим таблицы приращений
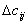 , полученных соответственно в результате выбора каждого столбца наименьшей стоимости и вычитания ее из всех стоимостей столбца, а также таблицу
, полученных соответственно в результате выбора каждого столбца наименьшей стоимости и вычитания ее из всех стоимостей столбца, а также таблицу 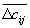 , получающихся в результате выбора в каждой строке
, получающихся в результате выбора в каждой строке 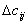 приращений и вычитании его из всех приращений строки при условии, что строки с
приращений и вычитании его из всех приращений строки при условии, что строки с
нулевым приращением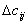
не рассматриваются.
- Заполнение проводится по столбцам, содержащим одно нулевое приращение, в клетки, содержащие его, записываются потребности, без учета величины запасов на складах. Затем уже с учетом произведенных постановок просматриваем столбцы, содержащие два нулевых и более приращений, и заполняем их, до тех пор, пока все объемы потребностей не будут закреплены за поставщиками.
- Подсчитываются для строк разницы между фактическими запасами и полученными для опорного “фиктивного” плана. Критерием оптимальности плана является нулевая разница по всем запасам и “фиктивным” планом. В случае положительной разницы строки называют недостаточными, в случае отрицательной разницы - избыточными, нулевыми строки называют в случае 0-разницы.
- Отмечаются столбцы, с занятыми клетками в избыточных строках. Для каждой недостаточной и нулевой строки просматриваются приращения
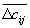 , стоящие в отмеченных столбцах, выбирается наименьшее в строке. Эти значения показывают, какое приращение стоимости будет получено на данном шаге, если единицу потребности перезакрепить от одного поставщика к другим (избыточные и недостаточные строки). Сравнивая
, стоящие в отмеченных столбцах, выбирается наименьшее в строке. Эти значения показывают, какое приращение стоимости будет получено на данном шаге, если единицу потребности перезакрепить от одного поставщика к другим (избыточные и недостаточные строки). Сравнивая 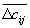 со значениями нулевой строки, получим два случая:
со значениями нулевой строки, получим два случая:
а) для каждой нулевой строки минимальное значение
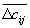 меньше либо равно по отношению к приращениям нулевой строки.
меньше либо равно по отношению к приращениям нулевой строки.б) минимальное приращение
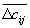 больше приращений нулевой строки;
больше приращений нулевой строки;В случае а) производится непосредственное перераспределение потребности из избыточной строки в недостаточную в клетку отмеченного столбца, которой соответствует минимальное
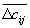
В случае б) составляются цепочки.
Для построения цепочки в нулевой строке в отмеченном столбце находим клетку, для которой разность меньше минимального значение
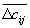 , и отмечаем ее знаком “+”, в этом же столбце находим занятую клетку, стоящую в избыточной строке, и отмечаем ее знаком “-” - начало цепочки. Начиная движение по построенному звену цепочки от “-” к “+”, попадаем в нулевую строку, затем передвигаемся по нулевой строке к занятой клетке и отмечаем ее знаком “-”, далее по столбцу переходим в клетку недостаточной строки и отмечаем ее знаком “+”.
, и отмечаем ее знаком “+”, в этом же столбце находим занятую клетку, стоящую в избыточной строке, и отмечаем ее знаком “-” - начало цепочки. Начиная движение по построенному звену цепочки от “-” к “+”, попадаем в нулевую строку, затем передвигаемся по нулевой строке к занятой клетке и отмечаем ее знаком “-”, далее по столбцу переходим в клетку недостаточной строки и отмечаем ее знаком “+”.Составляем для каждой цепочки алгебраическую сумму приращения, считая их отрицательными, если они стоят в клетке, отмеченной знаком “-”, и положительными, если клетка отмечена знаком “+”. Если сумма больше минимального
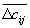 , то производится непосредственное распределение, если меньше, то распределение производится по цепочке.
, то производится непосредственное распределение, если меньше, то распределение производится по цепочке. - Исключаем из рассмотрения отмеченные столбцы. Если занятая клетка избыточной строка стала незанятой или избыточной , то начинаем п.4. В противном случае продолжаем процесс до тех пор, пока все строки не превратятся в нулевые
