Міністерство освіти І науки України Кіровоградський державний педагогічний університет імені Володимира Винниченка
| Вид материала | Документы |
- Міністерство освіти І науки україни «Переяслав – Хмельницький державний педагогічний, 554.03kb.
- Міністерство освіти І науки україни двнз«Переяслав – Хмельницький державний педагогічний, 1277.11kb.
- Міністерство освіти І науки, молоді та спорту україни уманський національний університет, 29.37kb.
- Міністерство освіти І науки україни полтавський державний педагогічний університет, 680.62kb.
- Міністерство освіти І науки україни переяслав-хмельницький державний педагогічний університет, 616.99kb.
- Міністерство освіти І науки України, 1659.87kb.
- Міністерство освіти І науки україни мелітопольський державний педагогічний університет, 2525.18kb.
- Південноукраїнський державний педагогічний університет імені К. Д. Ушинського (м. Одеса), 349.4kb.
- Міністерство освіти І науки, молоді та спорту україни уманський національний університет, 30.09kb.
- Міністерство освіти І науки України Слов’янський державний педагогічний університет, 2976.14kb.
10 (7 балів). Площа чотирикутника дорівнює 1м2, а периметр – 4м. Довести, що чотирикутник обов’язково є квадратом.
Н
 ехай
ехай  – даний чотирикутник,
– даний чотирикутник,  ,
,  ,
,  ,
,  .
.З нерівності
 легко видно, що
легко видно, що  .
.  . Аналогічно,
. Аналогічно,  . Додавши дві останні нерівності отримаємо:
. Додавши дві останні нерівності отримаємо:  . Рівність можлива, по-перше, коли всі кути прямі, а також при умові, що
. Рівність можлива, по-перше, коли всі кути прямі, а також при умові, що  , але
, але  і
і  , тому
, тому  ,
,  , тобто маємо прямокутник, у якого всі сторони рівні, тобто квадрат.
, тобто маємо прямокутник, у якого всі сторони рівні, тобто квадрат.1
 0 (4 бали). Нехай
0 (4 бали). Нехай  – точка на медіані
– точка на медіані  трикутника
трикутника  . Прямі
. Прямі  і
і  перетинають сторони
перетинають сторони  і
і  у точках
у точках  і
і  відповідно. Відомо, що площі трикутників
відповідно. Відомо, що площі трикутників  і
і  однакові. Довести, що
однакові. Довести, що  – точка перетину медіан трикутника
– точка перетину медіан трикутника  .
.Прямі
 ,
,  ,
,  перетинаються в одній точці, тому за теоремою Чеви:
перетинаються в одній точці, тому за теоремою Чеви:  , але
, але  , тому
, тому  , звідки
, звідки  . Нехай
. Нехай  – відстань між прямими
– відстань між прямими  та
та  , тоді
, тоді  ,
,  ,
,  , де через
, де через  позначено проекцію точки
позначено проекцію точки  на пряму
на пряму  . Отже,
. Отже,  – медіана, а тому
– медіана, а тому  – точка перетину медіан.
– точка перетину медіан.10 (4 бали). Чи існує трапеція, основи якої дорівнюють 9 см і 11 см, а бічні сторони 8 см і 6 см? Відповідь обґрунтуйте.
Н
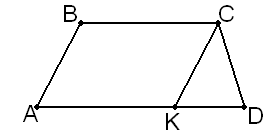 ехай
ехай  – дана трапеція.
– дана трапеція.  ,
,  ,
,  ,
,  . Побудуємо на основі точку
. Побудуємо на основі точку  так, що
так, що  , тоді
, тоді  – паралелограм,
– паралелограм,  , оскільки,
, оскільки,  ,
,  , то для
, то для  порушується нерівність трикутника
порушується нерівність трикутника  . Тобто такої трапеції не існує.
. Тобто такої трапеції не існує.1
 1 (4 бали). Діагоналі трапеції взаємно перпендикулярні. Одна з них дорівнює 6, а інша утворює кут
1 (4 бали). Діагоналі трапеції взаємно перпендикулярні. Одна з них дорівнює 6, а інша утворює кут  з основою. Знайти довжину середньої лінії трапеції.
з основою. Знайти довжину середньої лінії трапеції.Нехай
 – дана трапеція,
– дана трапеція,  – точка перетину діагоналей,
– точка перетину діагоналей,  , адже
, адже  .
.  ,
,  , звідки довжина середньої лінії:
, звідки довжина середньої лінії:  .
.9 (4 бали). Довжина кожної сторони трикутника не перевищує 1. Довести, що квадрат його площі не перевищує
 . Коли досягається знак рівності?
. Коли досягається знак рівності?Нехай
 - найменший кут трикутника. Тоді
- найменший кут трикутника. Тоді  і площа трикутника:
і площа трикутника:  . Знак рівності досягається при
. Знак рівності досягається при  - рівносторонній із сторонами 1.
- рівносторонній із сторонами 1.9 (4 бали). Дано коло радіуса
 . В нього вписано три однакових кола, кожне з яких дотикається до двох інших. Знайти радіуси цих кіл.
. В нього вписано три однакових кола, кожне з яких дотикається до двох інших. Знайти радіуси цих кіл.Н
 ехай
ехай  – радіус цих кіл.
– радіус цих кіл.  – радіус описаного кола для рівностороннього
– радіус описаного кола для рівностороннього  . Оскільки
. Оскільки  , маємо
, маємо  , звідси
, звідси 
 .
.11 (4 бали). Сторони
 і
і  опуклого чотирикутника
опуклого чотирикутника  рівні між собою. Довести, що прямі
рівні між собою. Довести, що прямі  і
і  утворюють рівні кути з прямою, що з’єднує середини
утворюють рівні кути з прямою, що з’єднує середини  і
і  .
.Н
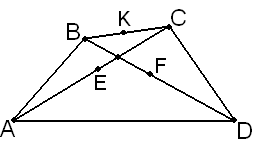 ехай
ехай  – середини відрізків
– середини відрізків  , відповідно. Оскільки
, відповідно. Оскільки  , то
, то  , але
, але  ,
,  , звідси випливає потрібне твердження.
, звідси випливає потрібне твердження.10 (4 бали). Довести, що площа правильного восьмикутника дорівнює добуткові його найкоротшої і найдовшої діагоналей.
Враховуючи осьову симетрію легко бачити, що
 ,
,  (
( ), побудуємо дотичні до описаного кола восьмикутника в точках
), побудуємо дотичні до описаного кола восьмикутника в точках  і
і  і в перетині з прямими
і в перетині з прямими  і
і  побудуємо прямокутник
побудуємо прямокутник  . Нехай
. Нехай 
 – проекція точки
– проекція точки  на пряму
на пряму  .
.  (
( ,
,  ). Звідки легко видно, що площа восьмикутника дорівнює площі прямокутника
). Звідки легко видно, що площа восьмикутника дорівнює площі прямокутника  , тобто
, тобто  .
.11 (4 бали). Чи можуть всі діагоналі опуклого шестикутника бути рівними за довжиною.
П
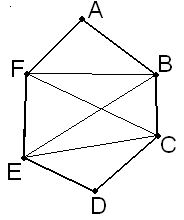 рипустимо, що це можливо, тоді рівнобедрені трикутники
рипустимо, що це можливо, тоді рівнобедрені трикутники  та
та  рівні (
рівні ( – спільна сторона,
– спільна сторона,  ), але тоді
), але тоді  ,
,  – суперечність. Ні, не можливо.
– суперечність. Ні, не можливо.10 (4 бали). В яких межах може змінюватись периметр трапеції, у якої діагоналі – бісектриси кутів при більшій основі, а одна з бічних сторін дорівнює 2.
В
 раховуючи властивість різносторонніх кутів, маємо:
раховуючи властивість різносторонніх кутів, маємо:  ,
,  . Аналогічно
. Аналогічно  .
.  , тому
, тому  . За нерівністю многокутника:
. За нерівністю многокутника:  ,
,  .
. Отже,
 . «Лівий» кінець досягається коли «зсувати» точки
. «Лівий» кінець досягається коли «зсувати» точки  та
та  до граничного положення, коли
до граничного положення, коли  . Для правого кінця потрібно «розсувати» точки
. Для правого кінця потрібно «розсувати» точки  та
та  до граничного положення, коли
до граничного положення, коли  .
.1
 1 (4 бали). Довести, що сума відстаней від довільної точки простору до всіх вершин одиничного куба не менша від
1 (4 бали). Довести, що сума відстаней від довільної точки простору до всіх вершин одиничного куба не менша від  .
. Обчислимо діагональ куба:
 .
. Розглянемо суму відстаней від довільної точки простору
 до усіх вершин одиничного куба та врахуємо нерівність трикутника, отримаємо:
до усіх вершин одиничного куба та врахуємо нерівність трикутника, отримаємо:  .
.1
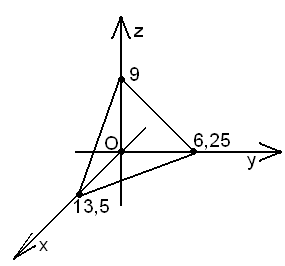 1 (4 балів). Поверхня кулі дотикається координатних площин та площини
1 (4 балів). Поверхня кулі дотикається координатних площин та площини  . Знайти центр вписаної кулі.
. Знайти центр вписаної кулі.Нехай
 – центр вписаної кулі. Точки
– центр вписаної кулі. Точки  і
і  лежать по один бік від площини
лежать по один бік від площини  , причому
, причому  , враховуючи відому формулу відстані від точки до площини отримаємо:
, враховуючи відому формулу відстані від точки до площини отримаємо:  ,
,  ,
,  .
.11 (7 балів). Довести, що
 , якщо
, якщо  – довжини сторін трикутника.
– довжини сторін трикутника.За нерівністю трикутника:
 ,
,  ,
,  . Піднісши ці нерівності до квадрату, та додавши, отримаємо:
. Піднісши ці нерівності до квадрату, та додавши, отримаємо: 
 .
.11 (7 балів). Знайти висоту конуса найбільшого об’єму, вписаного в кулю радіуса
 .
.Н
 ехай висота дорівнює
ехай висота дорівнює  . Розглянемо переріз, який проходить через вершину
. Розглянемо переріз, який проходить через вершину  і центр кулі
і центр кулі  . З
. З  :
:  , звідки
, звідки  . У випадку коли
. У випадку коли  – тупокутний, вираз для об’єму такий самий (перевірте!).
– тупокутний, вираз для об’єму такий самий (перевірте!).  ,
,  ,
,  ,
,  при
при  або
або  , тоді
, тоді  , це значення є максимальним.
, це значення є максимальним.