Geum.ru

Міністерство освіти І науки України Кіровоградський державний педагогічний університет імені Володимира Винниченка

Вид материалаДокументы
Подобный материал:
1   ...   13   14   15   16   17   18   19   20   21

11 (7 балів). Знайти об’єм трикутної піраміди , якщо ,

1 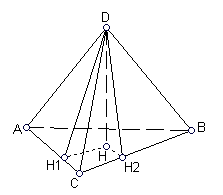спосіб. – прямокутний, бо ; нехай – висота піраміди.

Нехай – висота грані : , – висота грані : . Так як усі ребра піраміди відомі, то для кожної грані ми можемо обчислити (якщо потрібно) площу, висоти і ін.:

1) (кв.од.); обчислимо висоту грані: (од.);

(од.).

2) (кв.од.);

 (од.);  (од.).

3) ; ; – проекція , а отже .

Аналогічно ; – прямокутник (од.);

4) ;

 (од.).

5) ;  (кв.од.).;  (куб.од.).

2 спосіб. Об’єм піраміди . Використаємо метод координат (): нехай початок координат співпадає з точкою , вісь абсцис напрямлена від точки до , вісь ординат – від точки до , вісь аплікат – перпендикулярно до площини , тоді координати точок ; – відстань від точки до площини , а тому є висотою піраміди. Врахуємо умову задачі, отримаємо:



звідки знаходимо . А тоді висота  (од.), площа основи (прямокутного трикутника)  (кв.од.).; і об’єм  (куб.од.).


11 (7 балів). Знайти об’єм трикутної піраміди , якщо ,

Розв’язання: (метод координат) див. попередню задачу.

Відповідь:  (куб.од.).


11 (7 балів). Знайти об’єм трикутної піраміди , якщо ,

У позначеннях попередньої задачі.

Відповідь:  (куб.од.).


10 (4 бали). Нехай Знайти найбільше і найменше значення виразу

1 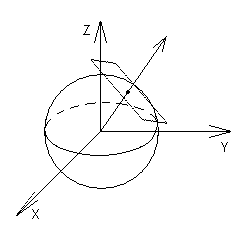спосіб: Рівняння прямої , що проходить через початок координат і перпендикулярна до сім’ї площин :

Параметри перетинів зі сферою , звідки або . Мінімум отримуємо при в точці

. Максимум – при , в точці .

2 спосіб: Використаємо нерівність Коші-Буняковського:

, а тоді . Максимум досягається, якщо , звідки маємо систему А тоді вираз перетворюється у . Звідки і точка, в якій досягається максимум, – . Аналогічно, мінімум отримаємо, якщо , а тоді і точка, в якій досягається мінімум ,– .


10 (7 балів). П’ять ребер трикутної піраміди однакові і дорівнюють 2 см. Якого найбільшого значення може набувати об’єм такої піраміди?

Н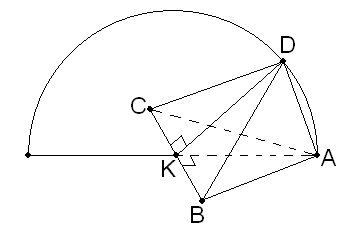ехай всі ребра, крім , мають фіксовану величину 2 см, – середина . і , . Отже, якщо провести через точку площину , перпендикулярну до ребра , і побудувати в ній коло , то найбільша відстань від точки до площини дорівнює , коли . Тому, (см3).


1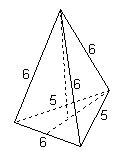1 (4 бали). Основою трикутної піраміди є трикутник зі сторонами 6см, 5см і 5см. Знайти висоту піраміди, якщо кожне її бічне ребро дорівнює 6см.

Оскільки всі бічні ребра однакові, то висота проектується в центр описаного кола.

В основі – рівнобедрений трикутник (сторони 6, 5, 5), висота, проведена до основи  6 см:  (см); (см2); (см).

(см).


11 (4 бали). Основа піраміди – паралелограм, сторони якого 16 і 22. Відстань від вершини піраміди до центра основи 4. Знаючи, що довжини бічних ребер виражаються непарними послідовними числами, знайдіть довжини бічних ребер піраміди.

Н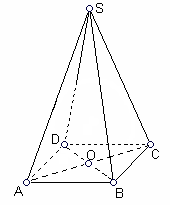ехай .

За теоремою косинусів:



або

. Звідки

.

– медіана і , . Тоді та . Додавши почленно та спростивши, матимемо: . Врахуємо, що , а тоді . За умовою бічні ребра виражаються послідовними непарними числами, тому маємо: , а тоді Умову задачі задовольняє , а тоді бічні ребра – дорівнюють .


10 (7 балів). Прямі, на яких лежать дві бісектриси внутрішніх кутів трикутника утворюють кут 40о, а прямі, на яких лежать дві його висоти, утворюють кут 55о. Знайти всі внутрішні кути трикутника..

Н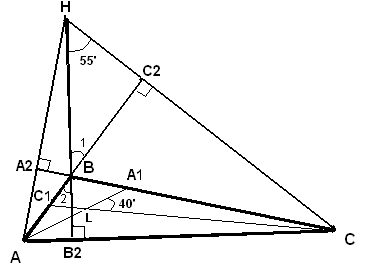ехай прямі - бісектриси, - точка перетину бісектрис. Тоді кут не може бути 40о, бо з сума двох інших кутів трикутника була б рівною 140о, а тоді сума двох кутів була б рівною 280о. Тому кут . Для цей кут є зовнішнім, а тому , а тоді

Нехай прямі - висоти , - точка перетину висот. Тоді в чотирикутнику кути , кут як кут, вертикальний до . Звідси маємо: (сума кутів 4-кутника 360о). А це є кут між висотами , тому кут між іншими двома висотами дорівнює 55о (за умовою задачі). Нехай це кут . Тоді з прямокутного трикутника визначаємо кут , тоді кут як вертикальний йому і з прямокутного , а тоді останній кут (або ).

Відповідь: .