Рабочая учебная программа по дисциплине 4 Задания на контрольные работы

Вид материала

Рабочая учебная программа

Содержание Задание №11 В случае разрыва функции в некоторой точке найти её пределы слева и справа, классифицировать характер разрыва Задание №12 таблица производных основных элементарных функций и правила дифференцирования Задание №13

Подобный материал:

• Рабочая программа, методические указания по выполнению курсовой работы и контрольные, 1000.11kb.
• Программа и контрольные задания по учебной дисциплине, 858.36kb.
• Программа и контрольные задания по учебной дисциплине «эконометрика» для студентов, 555.04kb.
• Рабочая программа методические указания контрольные задания для студентов специальности, 833.92kb.
• Программа и контрольные задания по учебной дисциплине «трудовое право» для студентов, 805.51kb.
• Программа и контрольные задания по учебной дисциплине «отечественная культура» для, 729.22kb.
• Рабочая программа По дисциплине «Стратегическое управление организацией» Для курса, 197.74kb.
• Программа и контрольные задания по учебной дисциплине «отечественная история» для студентов, 583.38kb.
• Программа, контрольные задания и тематика курсовых работ по учебной дисциплине основы, 557.3kb.
• Программа, методические указания и контрольные задания по дисциплине концепции современного, 717.75kb.

Пример 2. Найти .

Решение : Здесь неопределённость вида .Если к такой неопределённости сводится предел отношения двух многочленов при , нужно и в числителе и в знаменателе выделить критический множитель (x-x₀) и сократить на него числитель и знаменатель дроби. Выделяем критический множитель (x-3)



Опять возникла та же неопределённость. Действуя аналогично, получаем:



Ответ: .

Пример 3. Найти

Решение : Неопределённость. В этом случае нужно либо в числителе, либо в знаменателе дроби избавиться от иррациональных выражений, которые в точке обращаются в нуль. Чтобы раскрыть эту неопределённость, умножим и разделим дробь на выражение, сопряжённое числителю.

.

Теперь неопределённость создаёт критический множитель. Выделим его в числителе и знаменателе дроби, а затем сократим на него числитель и знаменатель.



Ответ: L=.

Пример 4. Найти пределы а) б) .

Решение: Неопределённость вида .

а) При . Умножая и числитель и знаменатель дроби на 8, приведём заданный предел к первому замечательному пределу .



Иногда для раскрытия неопределённости приходится предварительно применять тригонометрические формулы. В случае б) в числителе воспользуемся формулой и получим



Полагая и учитывая, что при , окончательно получим



Ответ: а) , б) .


Пример 5. Найти предел .

Решение : Неопределённость вида .Для раскрытия этой неопределенности используется второй замечательный предел. Выделяем в круглых скобках целую часть



Обозначим . Если , то и . Далее показатель степени умножаем и делим на .



Делаем замену переменной и . Находим предел показателя степени



.

Ответ:

ЗАДАНИЕ №11

Следующая задача контрольной работы такого типа:

Задана функция . Установить, является ли данная функция непрерывной.

В случае разрыва функции в некоторой точке найти её пределы слева и справа, классифицировать характер разрыва. Построить схематично график функции.

Любая элементарная функция непрерывна во всех точках своей области определения.

Необходимое и достаточное условие непрерывности функции в точке



Скачок функции в точке



Пример 1. Пусть функция имеет вид



Решение: Функция определена для всех . Если , то , поэтому для всех функция непрерывна . Если , непрерывна для всех .Если, для всех также непрерывна .Поэтому точки разрыва могут быть только для тех значений , в которых заданная функция меняет свой аналитический вид, а именно в точках и . Исследуем непрерывность функции в точке . Для этого найдём: предел слева

,

предел справа



.

Так как пределы слева и справа конечны, равны между собой и равны значению функции в точке , то получаем, что функция непрерывна в точке .

Пусть . Находим аналогично

Предел слева

,

Предел справа



Так как пределы слева и справа конечны, но не равны между собой, то в точке функция имеет разрыв первого рода со скачком.

.

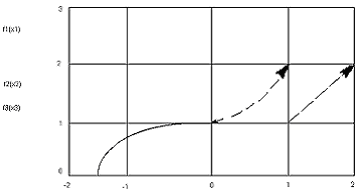
Строим график функции , выделяя области определения составляющих

функций стрелками, если они не определены в точке или .




ЗАДАНИЕ №12

Следующая задача относится к вычислению производных.

Пусть функция y=f(x) определена в некоторой окрестности точки «x».

Производной функции y=f(x) в точке «x» называется предел отношения приращения функции к соответствующему приращению аргумента , при стремлении к нулю.



Производная функции f(x) в точке x существует, если f(x) непрерывна в точке x и



Для отыскания производных элементарных функций используется таблица производных основных элементарных функций и правила дифференцирования.

1.	10.
2.	11.
3.	12.
4.	13.
5.	14.
6.	15.
7.	16.
8.	17.
9.	18.

Основные правила дифференцирования:

Для дифференцируемых в точке x функций f(x) и g(x) справедливы равенства:









Производная сложной функции где - промежуточный аргумент. Если существуют и , то

или

Производная обратной функции. Если для функции y=f(x) существует обратная функция , которая имеет в точке y производную , то

или

Дифференцирование неявной функции. Пусть уравнение



определяет y как неявную функцию от x, т.е. y=f(x) – неизвестная дифференцируемая функция и F(x,y) сложная функция. Дифференцируем по x обе части и получаем уравнение первой степени относительно , из которого легко находится - производная искомой функции.

Производная параметрически заданной функции x=x(t), y=y(t), - параметр. Если существуют производные и , то



Пример 1. Найти производные следующих функции:

а) , б) , в)

Решение: а) . Наша функция является суммой двух функций. Воспользуемся свойством производной суммы



Константу вынесем за знак производной и получим две производные сложных функций:



Поскольку внешняя функция в первом слагаемом – степенная, а во втором – натуральный логарифм, то для , и , по формуле дифференцирования сложной функции получим:



б) . Здесь мы воспользуемся свойством производной произведения двух функций , где - есть производная сложной функции, внешняя функция которой показательная, а внутренняя – степенная.



в) , . Производную функции, заданной параметрически, находим, учитывая, что , - сложные функции.



ЗАДАНИЕ №13

Найти пределы функции, применяя правило Лопиталя.

Для раскрытия неопределённостей вида или используется правило Лопиталя:

Пусть и две дифференцируемые на некотором интервале функции, причем , и пусть при (или ), обе эти функции стремятся к нулю (или ). Тогда, если при данном стремлении x существует, то существует и

.