Geum.ru

П. А. Бокарев Краткий конспект

Вид материалаКонспект

Содержание


Постановка транспортной задачи
Метод северо-западного угла (ручной)
Метод кольцевых маршрутов
Подобный материал:
1   ...   7   8   9   10   11   12   13   14   ...   17

    1. Постановка транспортной задачи



Классическая транспортная задача ставится в следующем виде:

пусть, имеется m – поставщиков (источников), и n – потребителей.

каждый поставщик имеет мощность ai, i = 1,m, а каждый потребитель нуждается в bj единиц ресурса, j =1,n.

известна стоимость перевозки единицы груза от i – ого поставщика j – ому потребителю - Cij,

Требуется назначить перевозки - Xij – объём перевозки из i в j, таким образом. что бы максимально израсходовать мощности источников, максимально удовлетворить потребителя и при этом стоимость перевозки была бы минимальной.

Формализовано транспортная задача может быть записана в следующем виде:









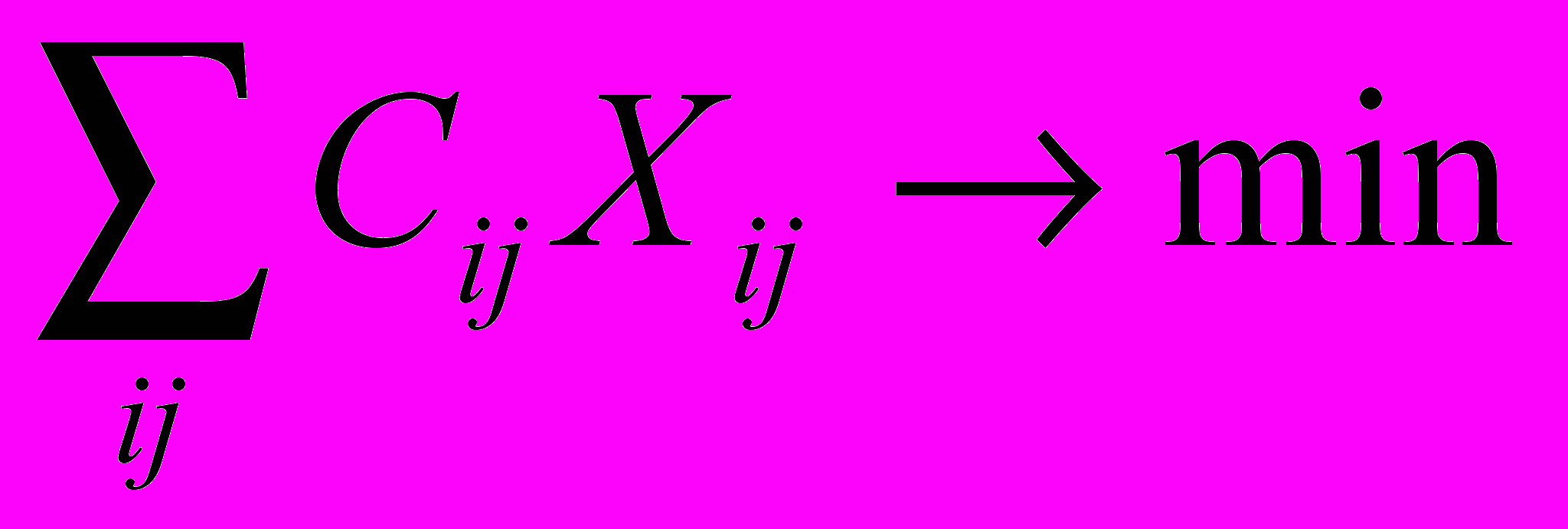
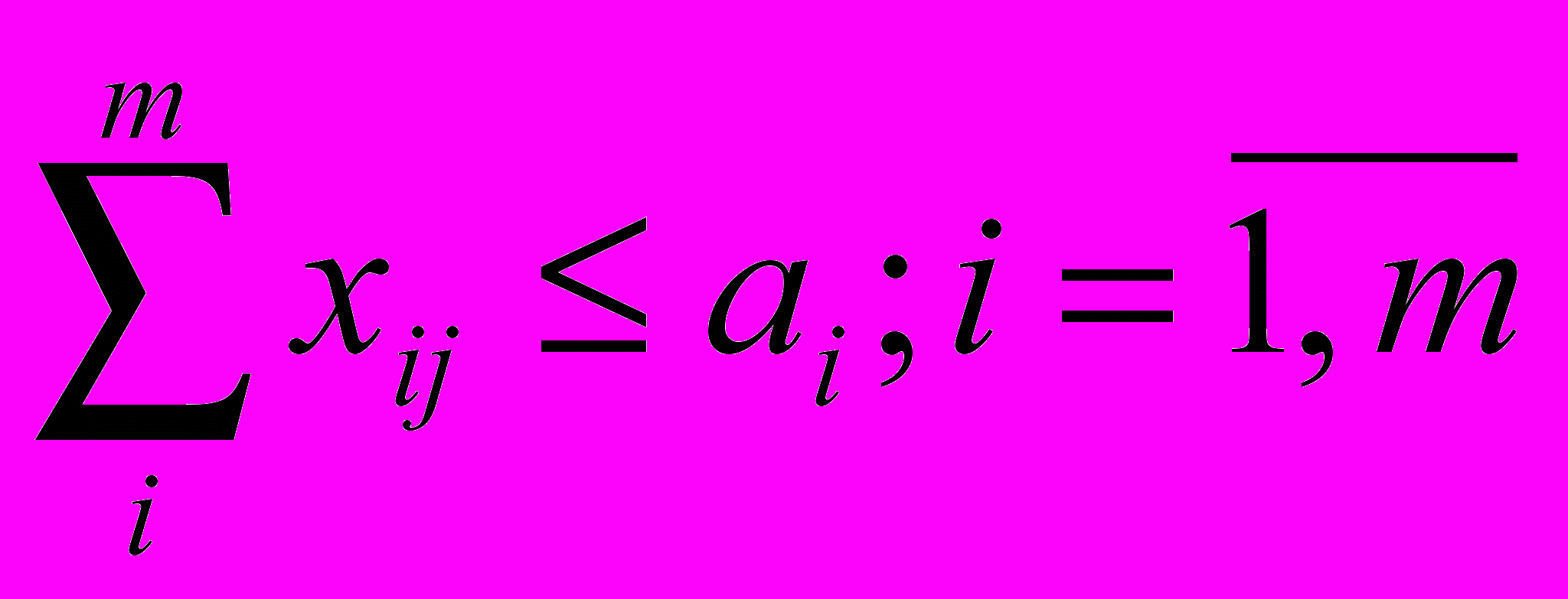
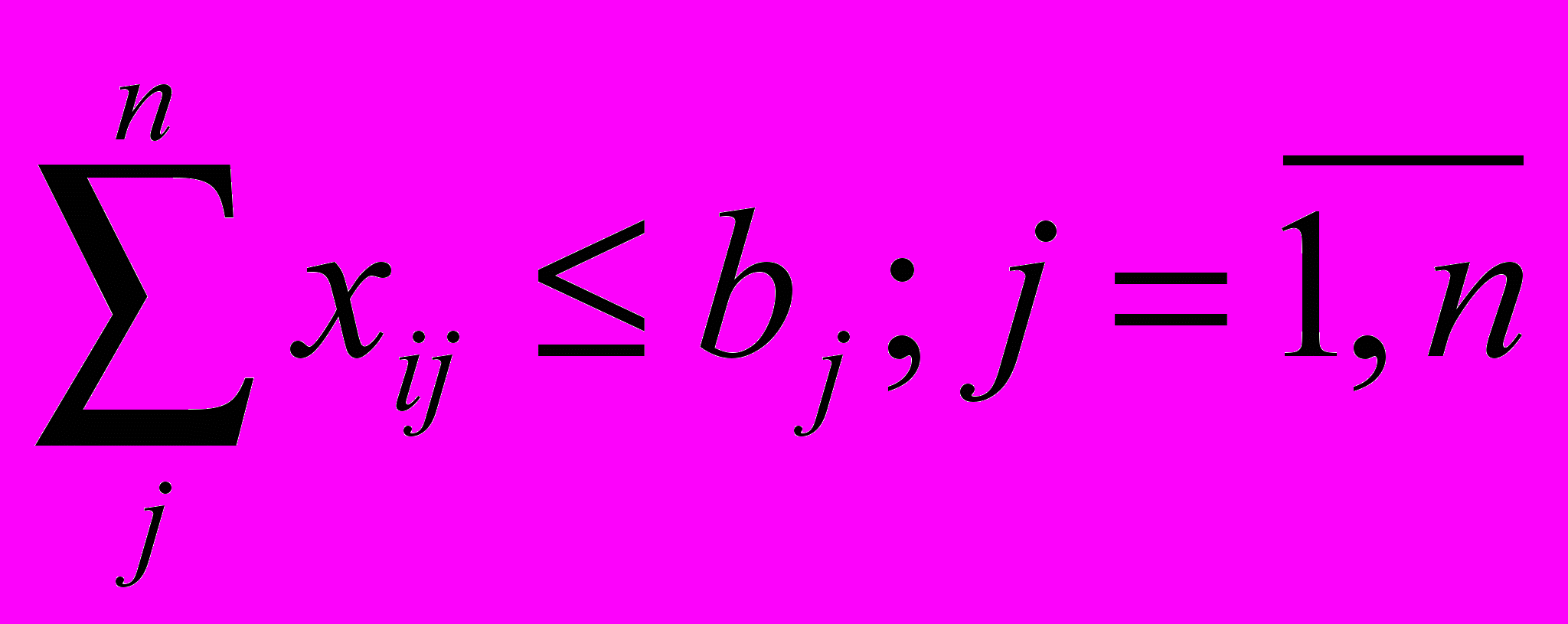
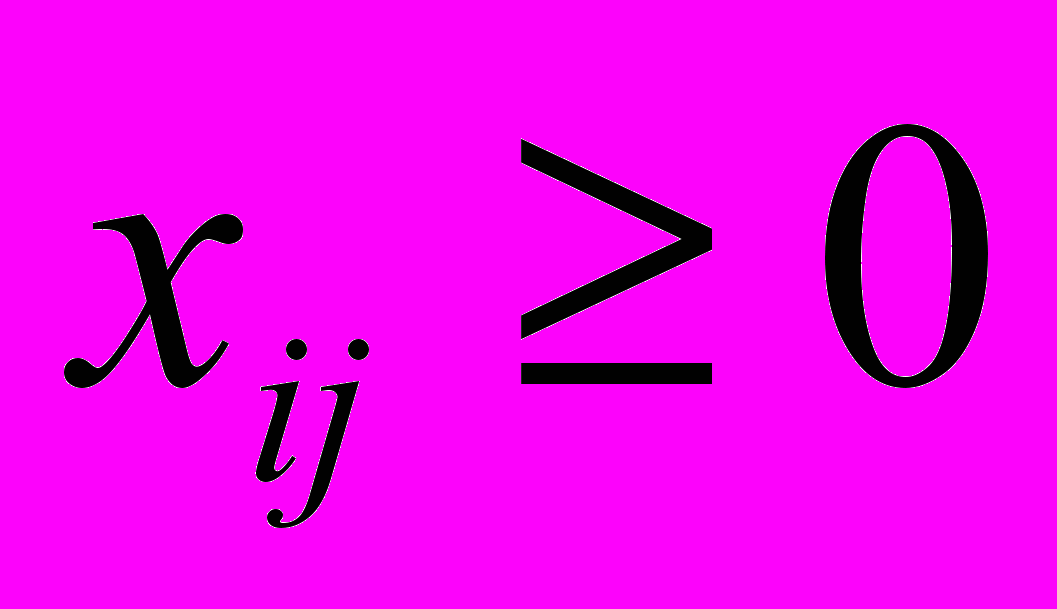
Полученная задача имеет оптимальное решение при всех нулевых перевозках, что не имеет экономической целесообразности. Необходимо скорректировать ограничения задачи с учетом того, что в общем случае суммарная мощность источников не равна суммарной потребности.

Получим три возможные постановки транспортной задачи:
  1. :









  1. :









  1. :










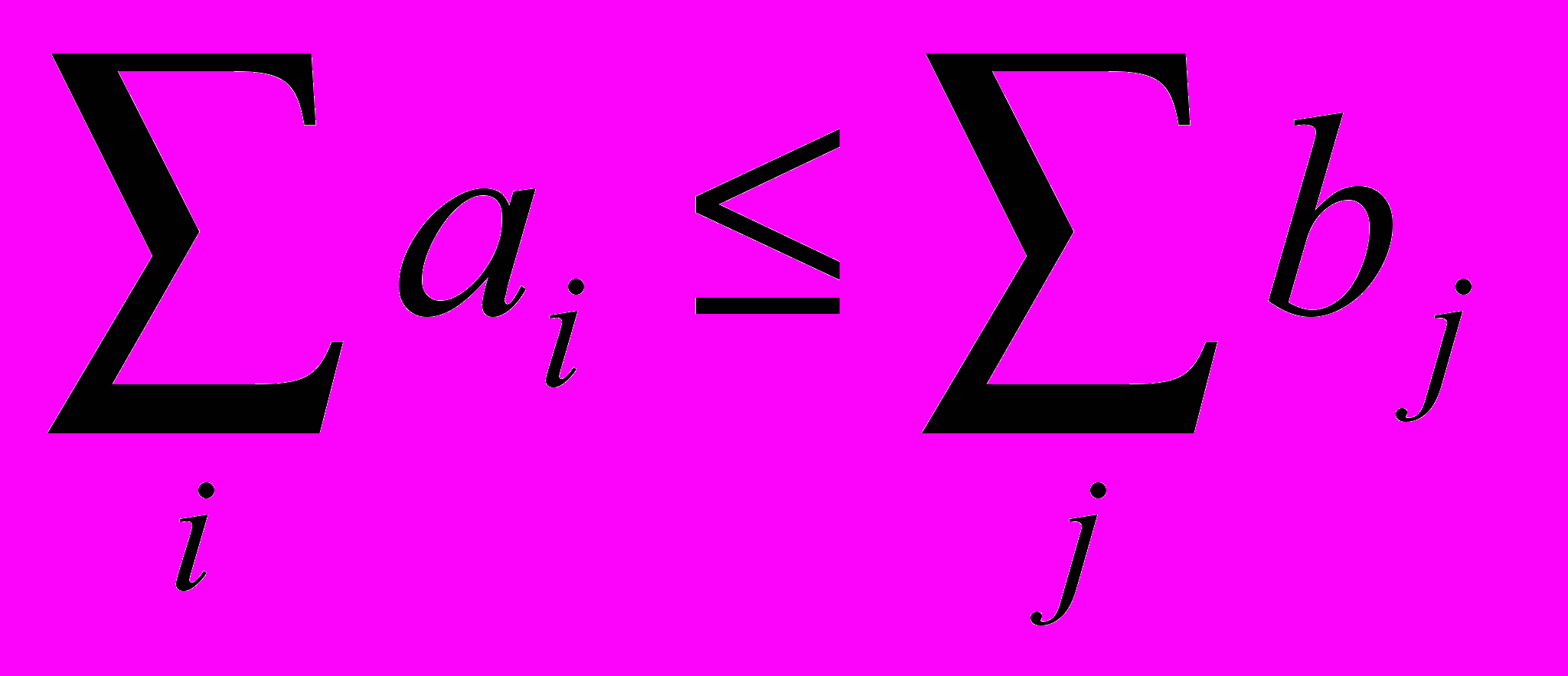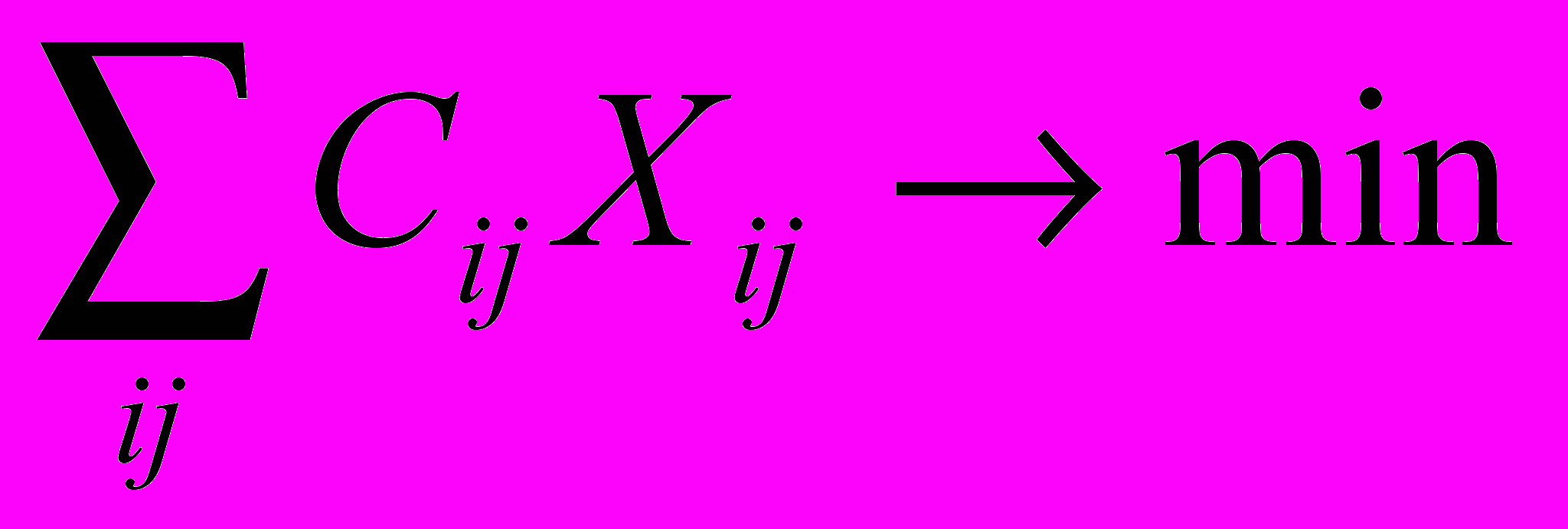
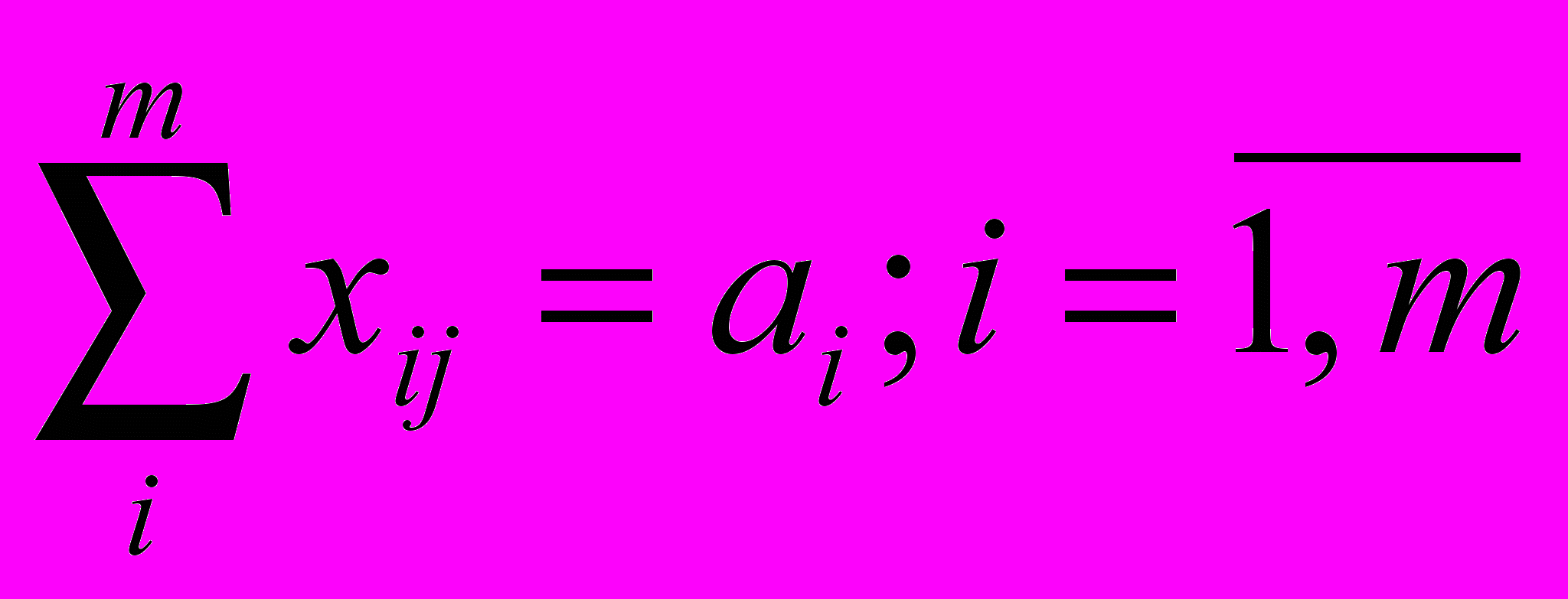
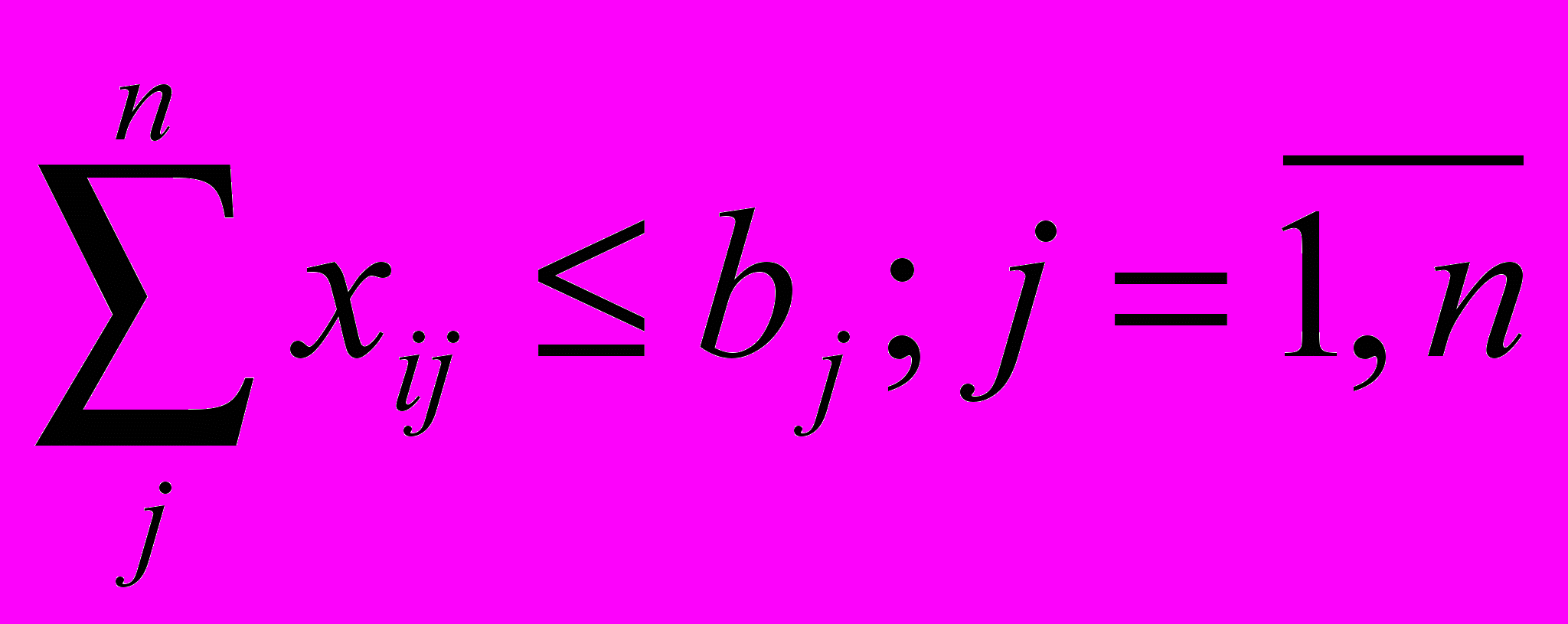
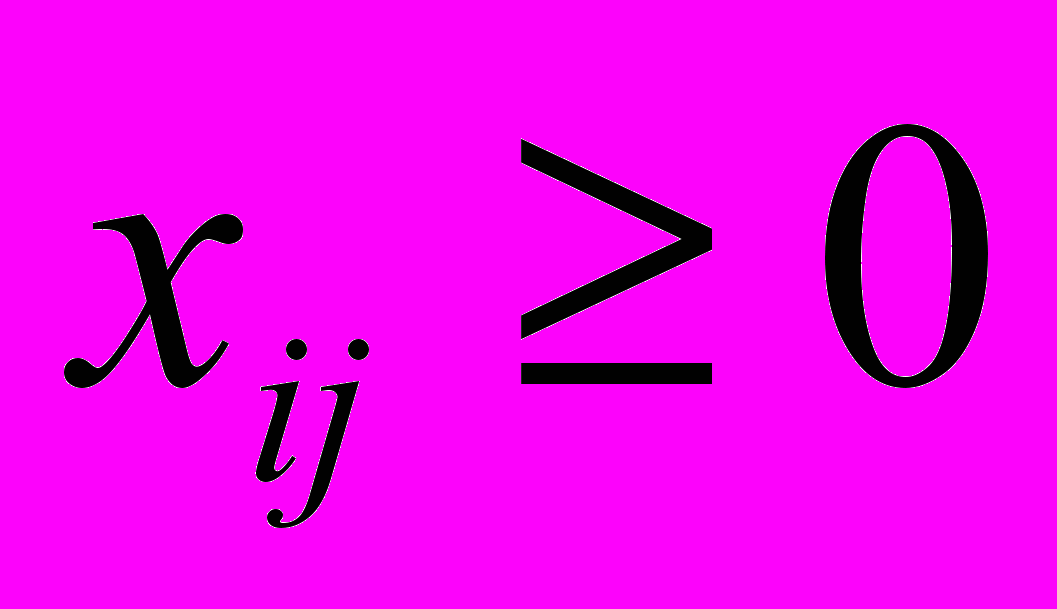
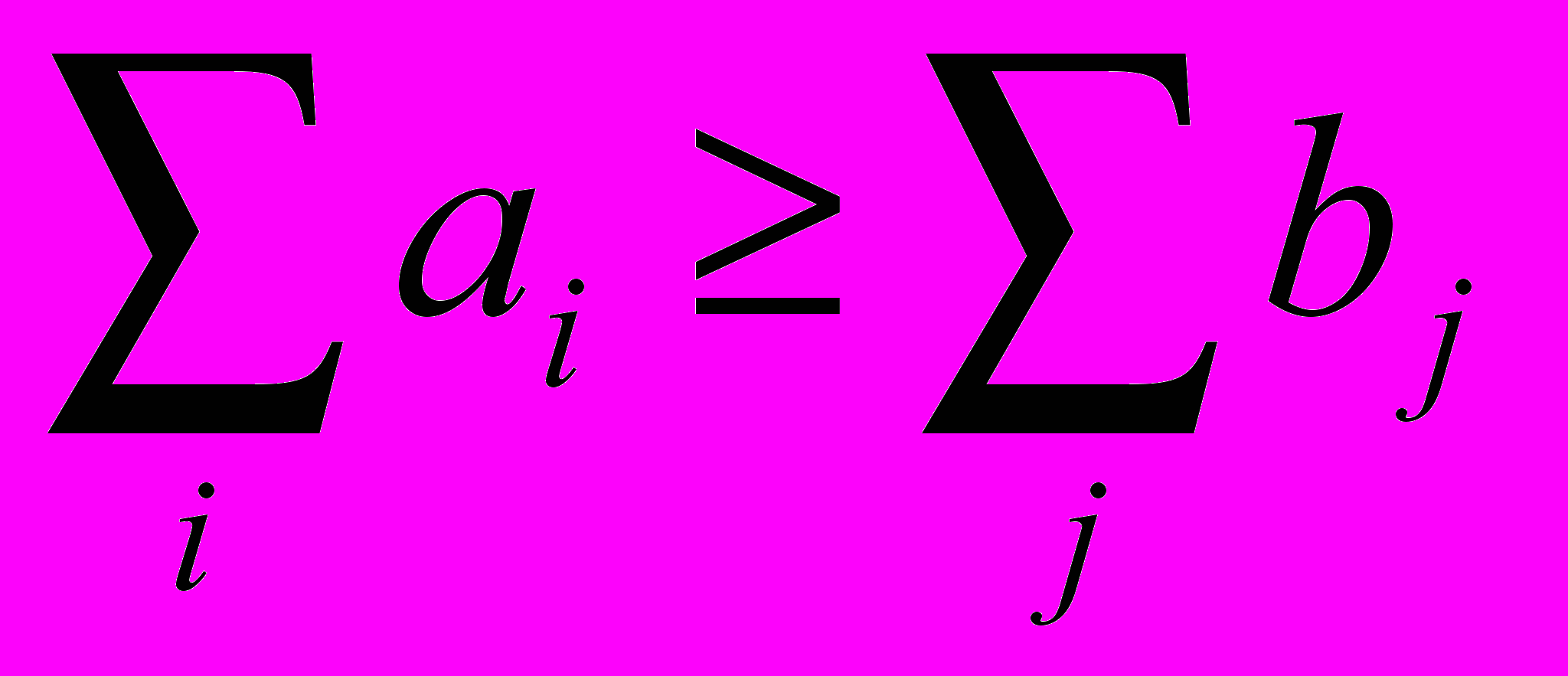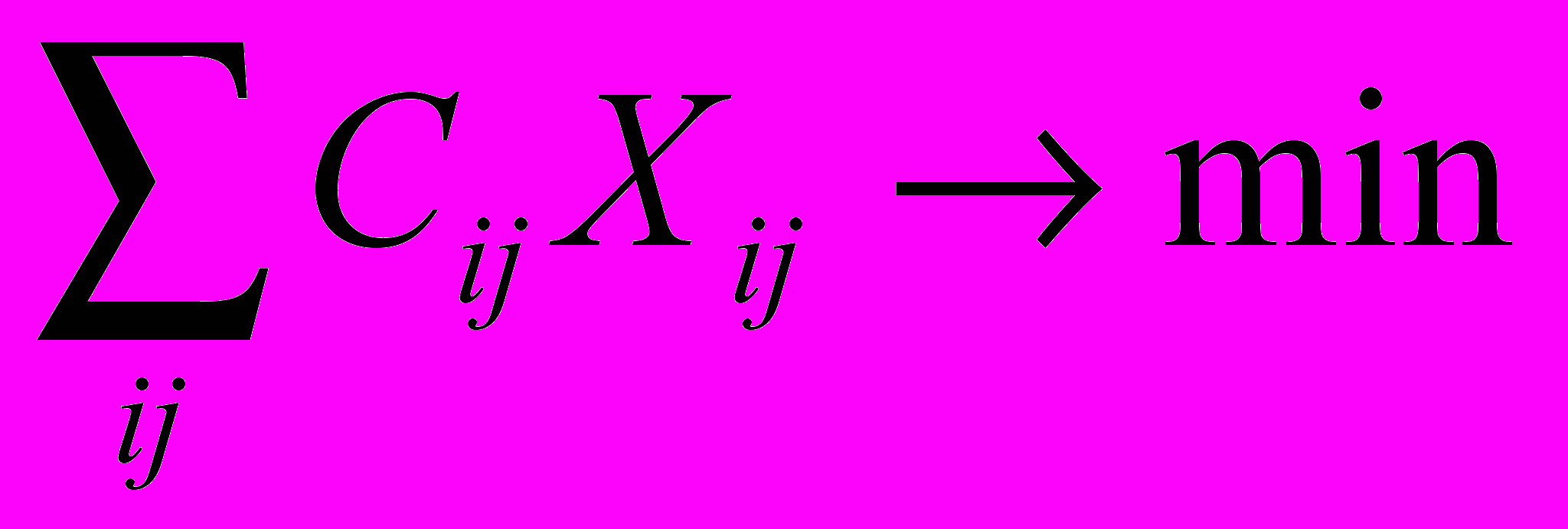
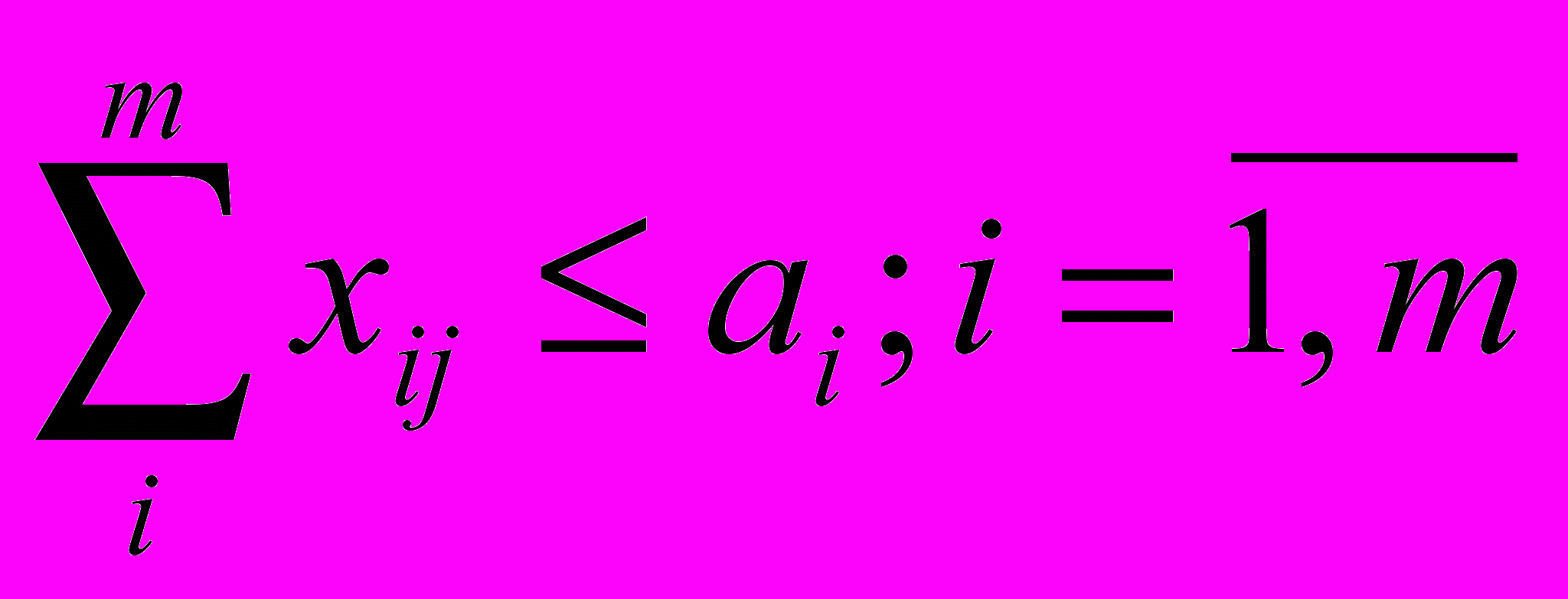
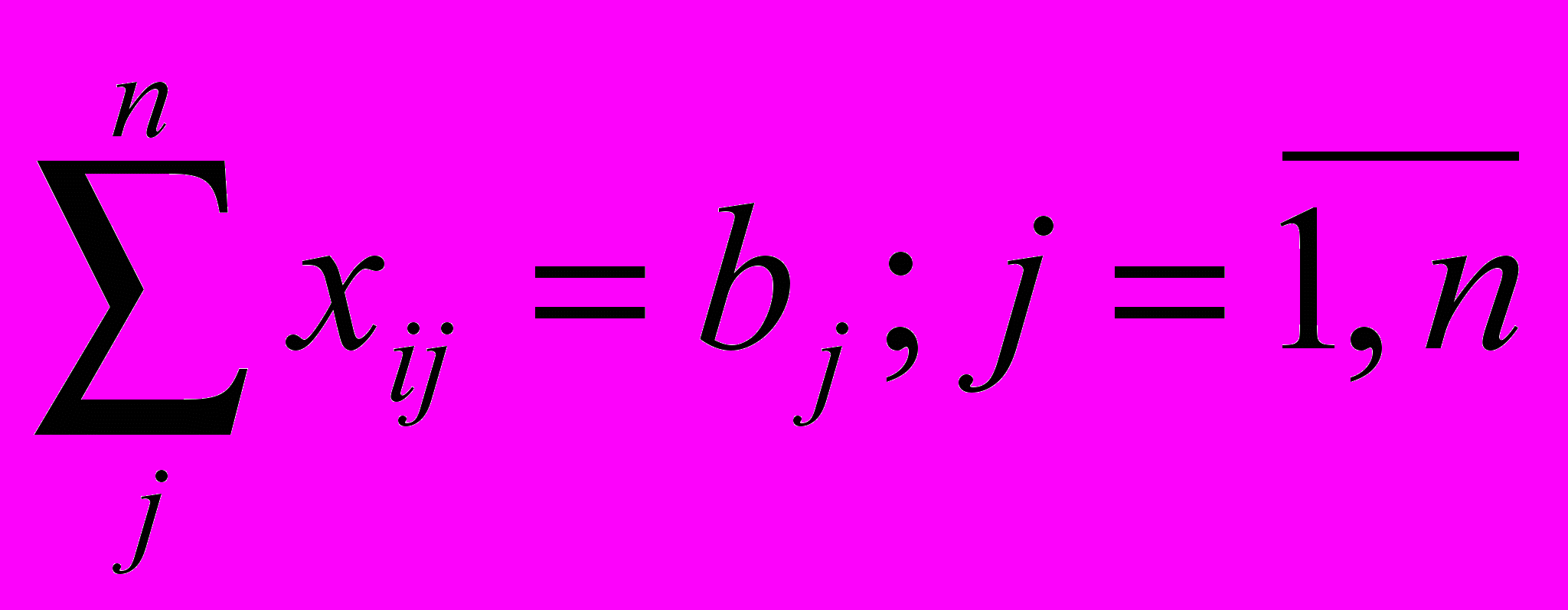
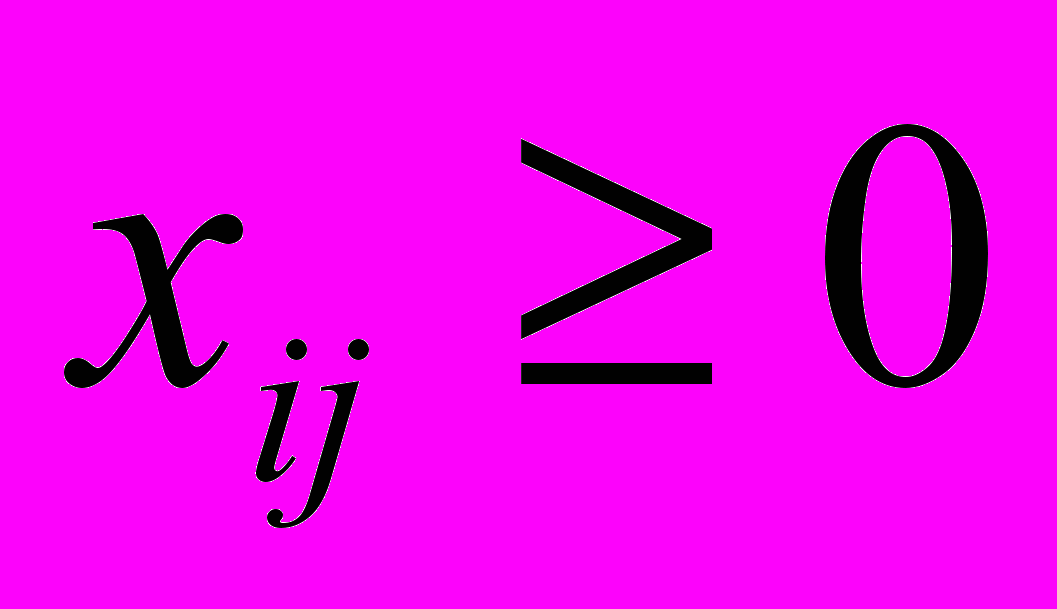
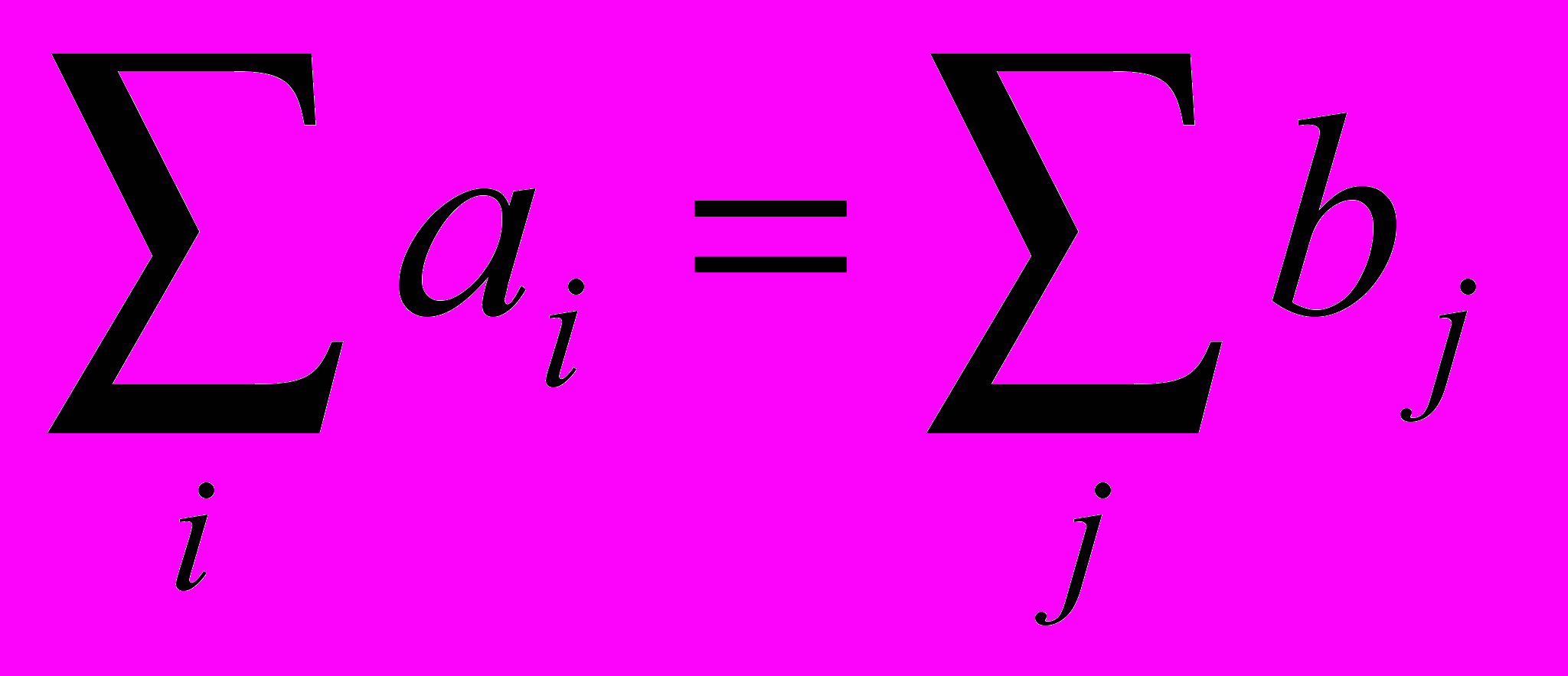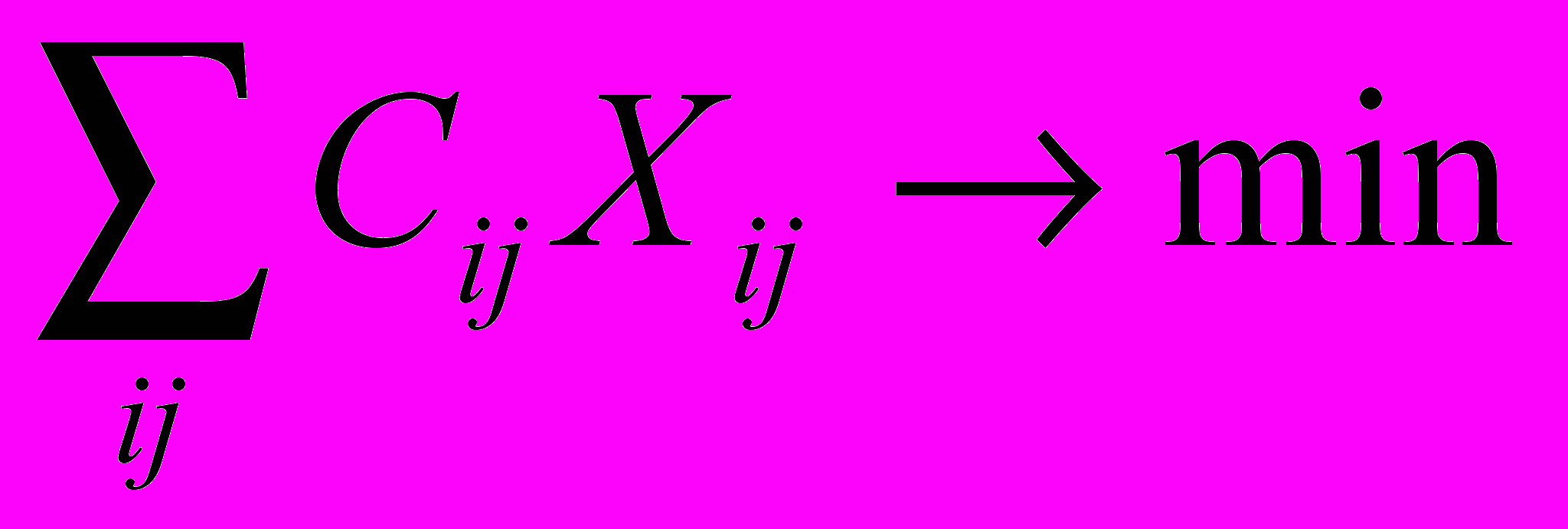
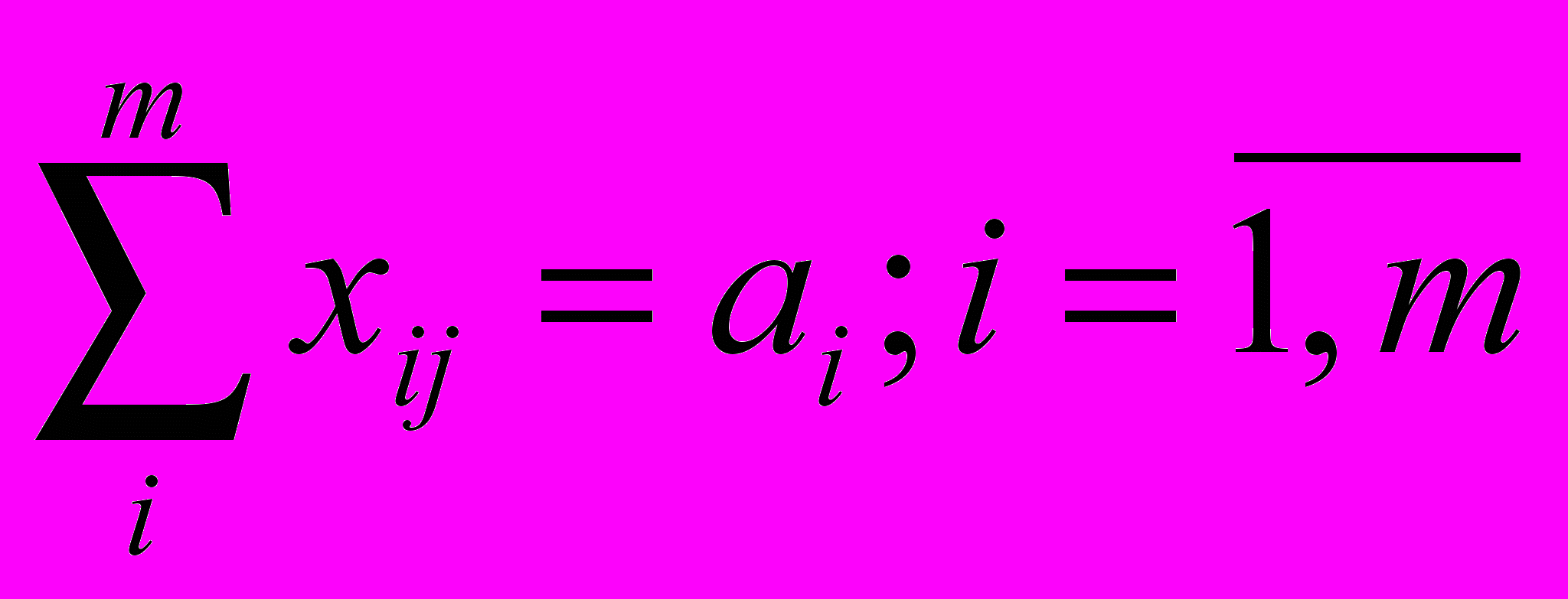
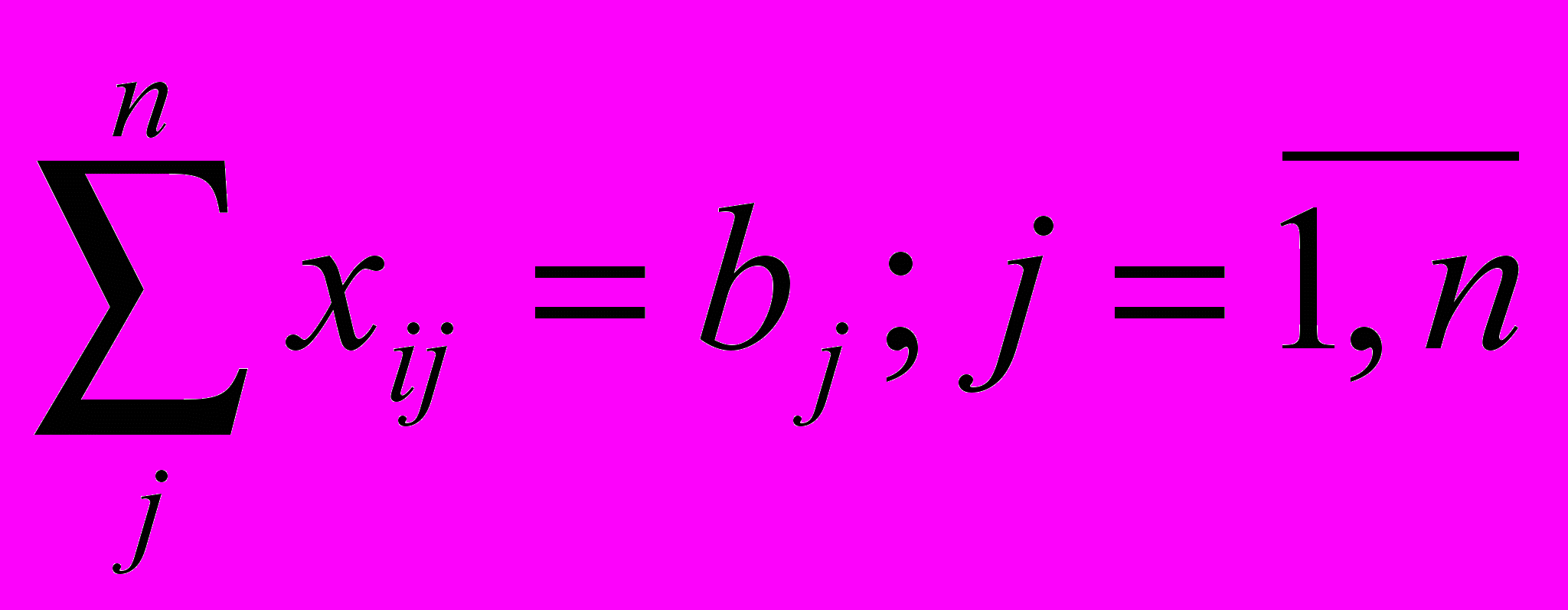
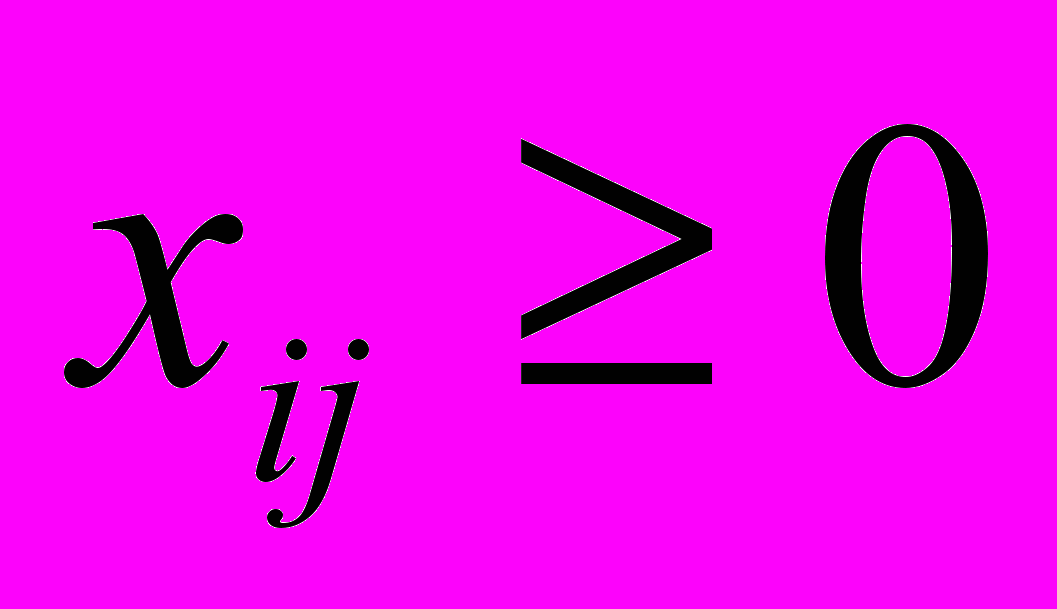
Классические задачи, сводящиеся к транспортным:

1) Задача о «ранце» (портфеле)

Есть собравшийся в поход турист, который должен упаковать в ранец различные полезные предметы. Причем может понадобиться несколько одинаковых предметов (n - предметов и m – ограничений);

2) Задача о назначении

Имеется n – самолетов и m – авиалиний. Известно, что на j – авиалинии i – тый самолет будет приносить доход Cij. Требуется распространить самолеты между авиалиниями таким образом, чтобы доход был max;

3) Задача о коммивояжере

Имеются города пронумерованные от 0…n. Выехав из города “0” коммивояжер должен побывать в каждом из них по 1 разу и вернуться в исходный город. Известно расстояние между городами. Требуется найти самый короткий маршрут;

4) Задача о “красках”

Дана плоская географическая карта. Границы каждой страны представляют замкнутую непрерывную кривую. Страны называются соседними, если у них есть общая граница. Требуется так раскрасить карту в 4 цвета, чтобы соседние страны были раскрашены в разные цвета.

Метод северо-западного угла (ручной)


1) Замкнуть задачу.



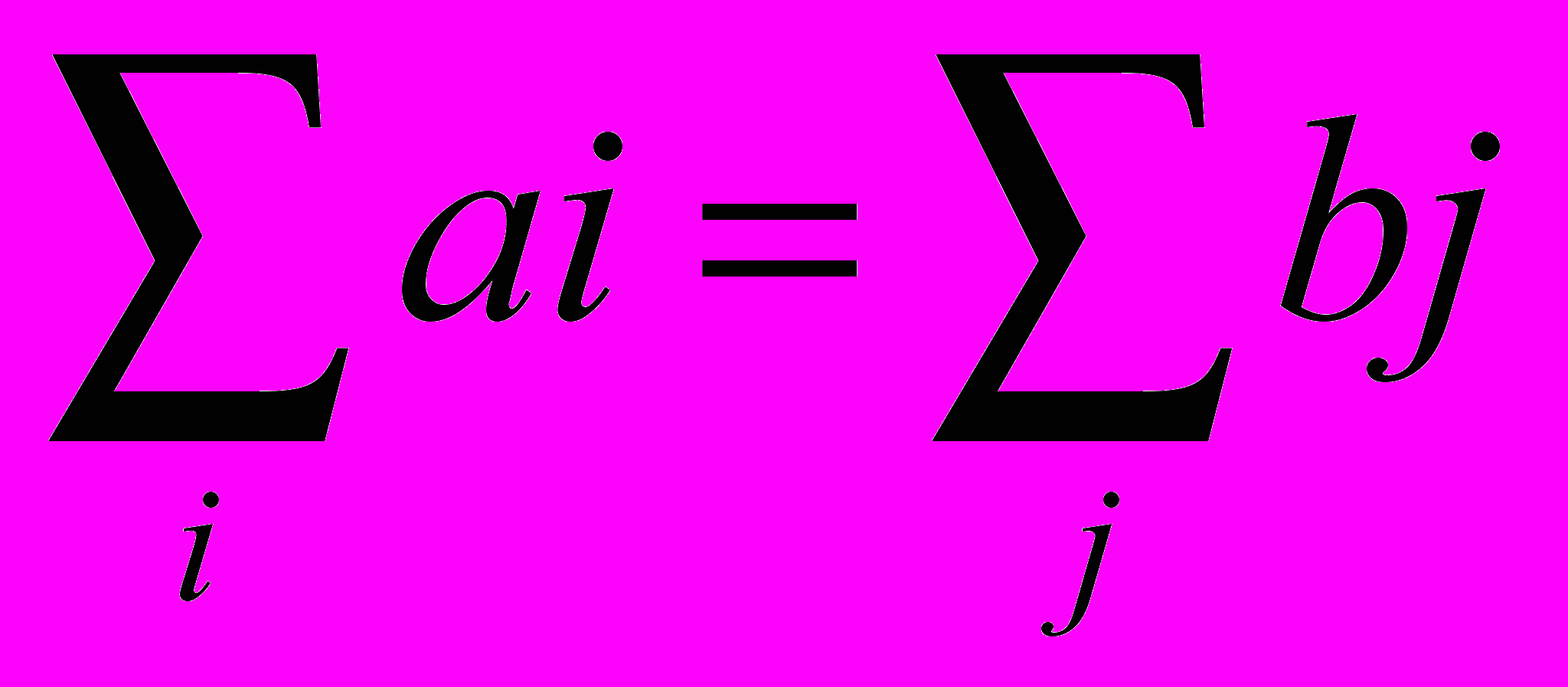
2) Заполнение матрицы начинается с северо-западного угла.

Перевозка назначается так, чтобы максимально израсходовать мощности поставщика или максимально удовлетворить потребности потребителя. Пока потребность не удовлетворена, поставки другим потребителям не назначаются. При полном удовлетворении потребителя либо израсходования мощности поставщика соответствующий столбец или строка платежной матрицы вычеркивается. Алгоритм начинается заново. Полученное решение проверяется на оптимальность методом замкнутых контуров, и проверяется на невырожденность. Решение является невырожденным, если содержит (m + n - 1) назначений. При необходимости решение корректируется.

Метод кольцевых маршрутов


В методе тестируется каждая нулевая перевозка на предмет возможности уменьшения издержек при назначении перевозки в данную клетку.

Алгоритм метода
  1. Выбирается неиспользованная клетка.
  2. Эта клетка оценивается
  3. Начиная с выбранной клетки, прокладывается кратчайший замкнутый путь через использованные клетки. Разрешаются только горизонтальные и вертикальные движения. Начиная со знака «+» в тестируемой клетке расставляем, чередуя, знаки «+» и «-» в каждом прямом углу заданного маршрута. В соответствии с проставленными знаками суммируем значения платежной матрицы, получая значение индекса маршрута. Шаги повторяются, пока не будут подсчитаны индексы для каждой перевозки.
  4. Маршрут с наименьшим отрицательным индексом позволит уменьшить издержки при его использовании. Если все индексы неотрицательные, то найденное решение оптимально.