Geum.ru

Удк 519. 2 Моделирование причинно-следственных связей, возникающих при анализе рисков

Вид материалаАнализ

Содержание


Постановка задачи
Библиографический список
Подобный материал:
УДК 519.2

Моделирование причинно-следственных связей, возникающих при анализе рисков

Лупач Денис Юрьевич,

ПГНИУ, E-mail: lupachdu@rambler.ru.


Аннотация: В статье рассматривается метод построения, анализа и отбора многомерных моделей для прогнозирования рисков.

Введение


Анализ существующих литературных источников показывает, что активная хозяйственная и социальная деятельность тесно связана с понятием риска. Термин «риск» получил широкое распространение в научной литературе и повседневной жизни. Для различных областей жизнедеятельности определяют огромное количество специфических рисков, отражающих частные особенности неблагоприятных ситуаций различных отраслей и видов деятельности. Величину риска нельзя непосредственно измерить, а можно лишь с некоторой надежностью оценить, используя количественные характеристики факторов риска и показатели откликов, находящихся под воздействием этих факторов. В существующей на сегодняшний день литературе под оценкой риска чаще всего понимается использование доступной информации и научно-обоснованных прогнозов для оценки воздействия социально-экономических факторов на функционирование исследуемой системы.

Количественная оценка риска осуществляется, как правило, методами математической статистики, поскольку невозможно одновременно учесть воздействие всех возможных факторов на отклик. В связи с этим возникают статистические зависимости, исследование которых занимает основное место при построении всех процедур и методов оценивания рисков. Одним из наиболее эффективных методов, используемых для построения моделей, описывающих причинно-следственные связи, при решении задачи оценивания рисков является метод регрессионного анализа [1].

Постановка задачи


Функционирование реальной системы, как правило, можно описать набором переменных, среди которых выделяются:

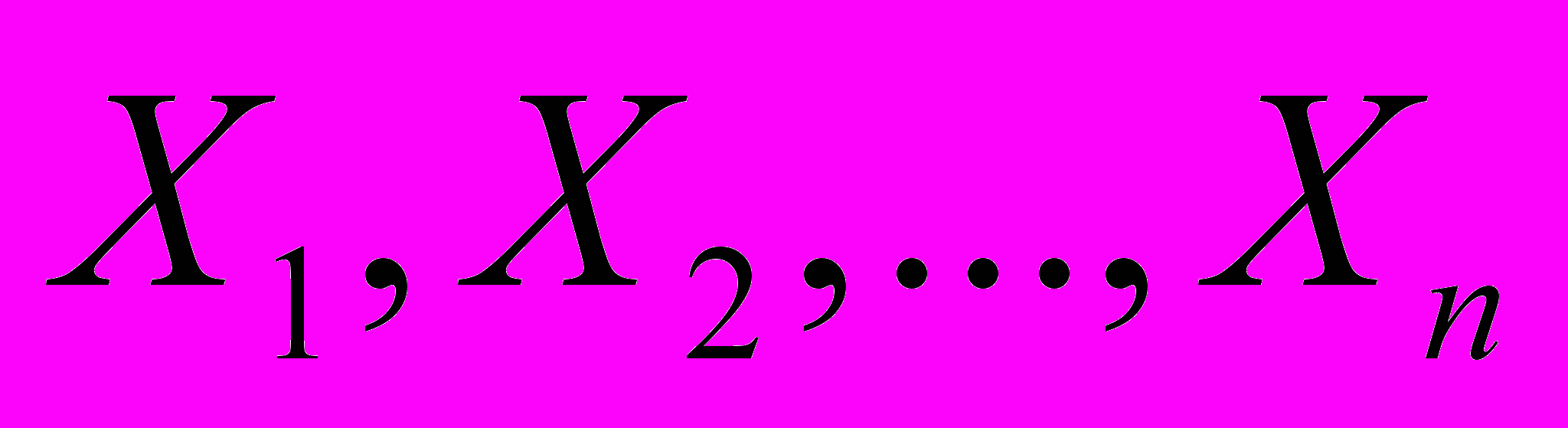– управляющие факторы;

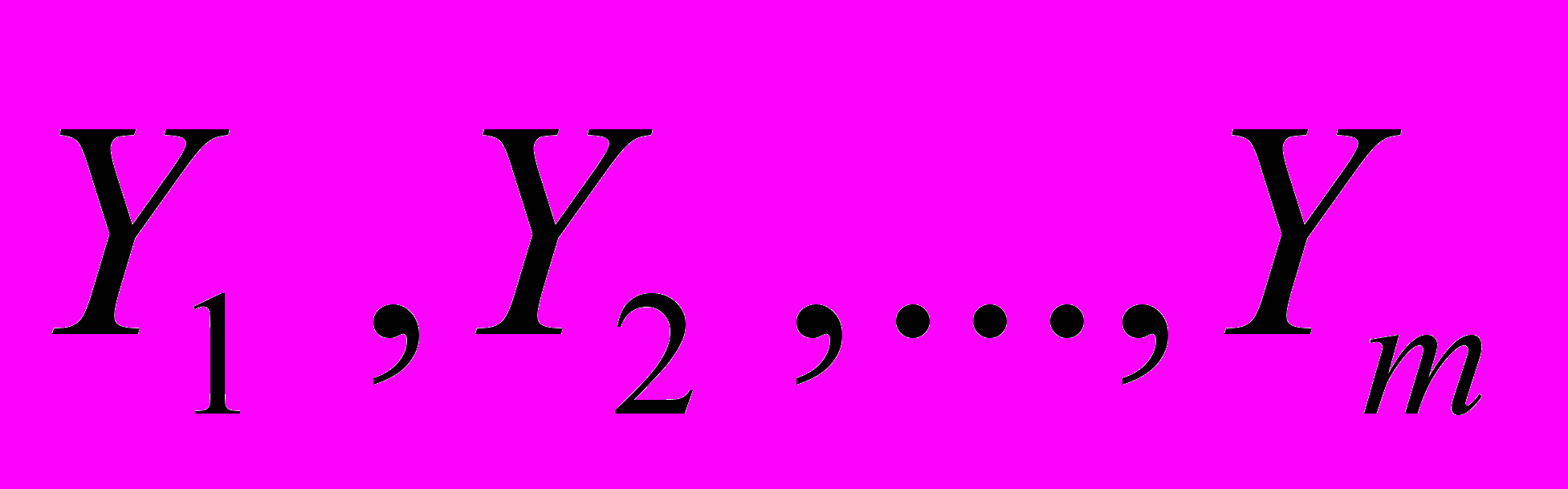– ответы (факторы, которые откликаются на воздействие управляющих факторов);

ζ1, ζ2, ζ3, …, ζm – латентные (то есть скрытые, не поддающиеся непосредственному измерению) случайные компоненты, отражающие влияние на 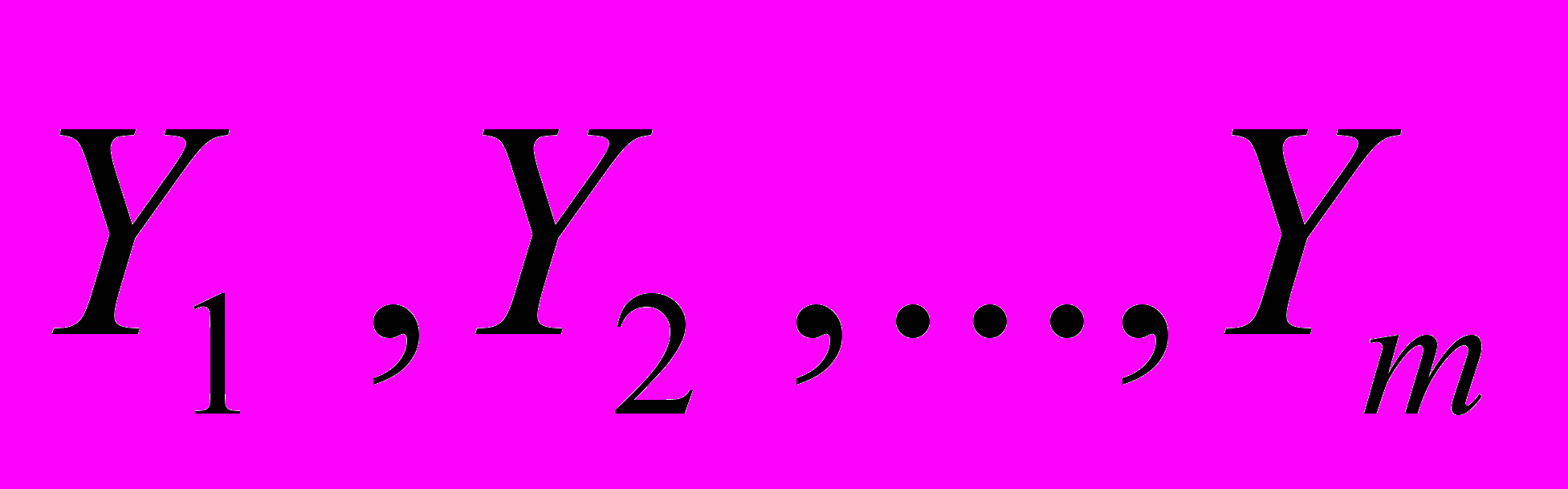неучтенных факторов (как правило, они называются «остатками»).

Определим матрицу 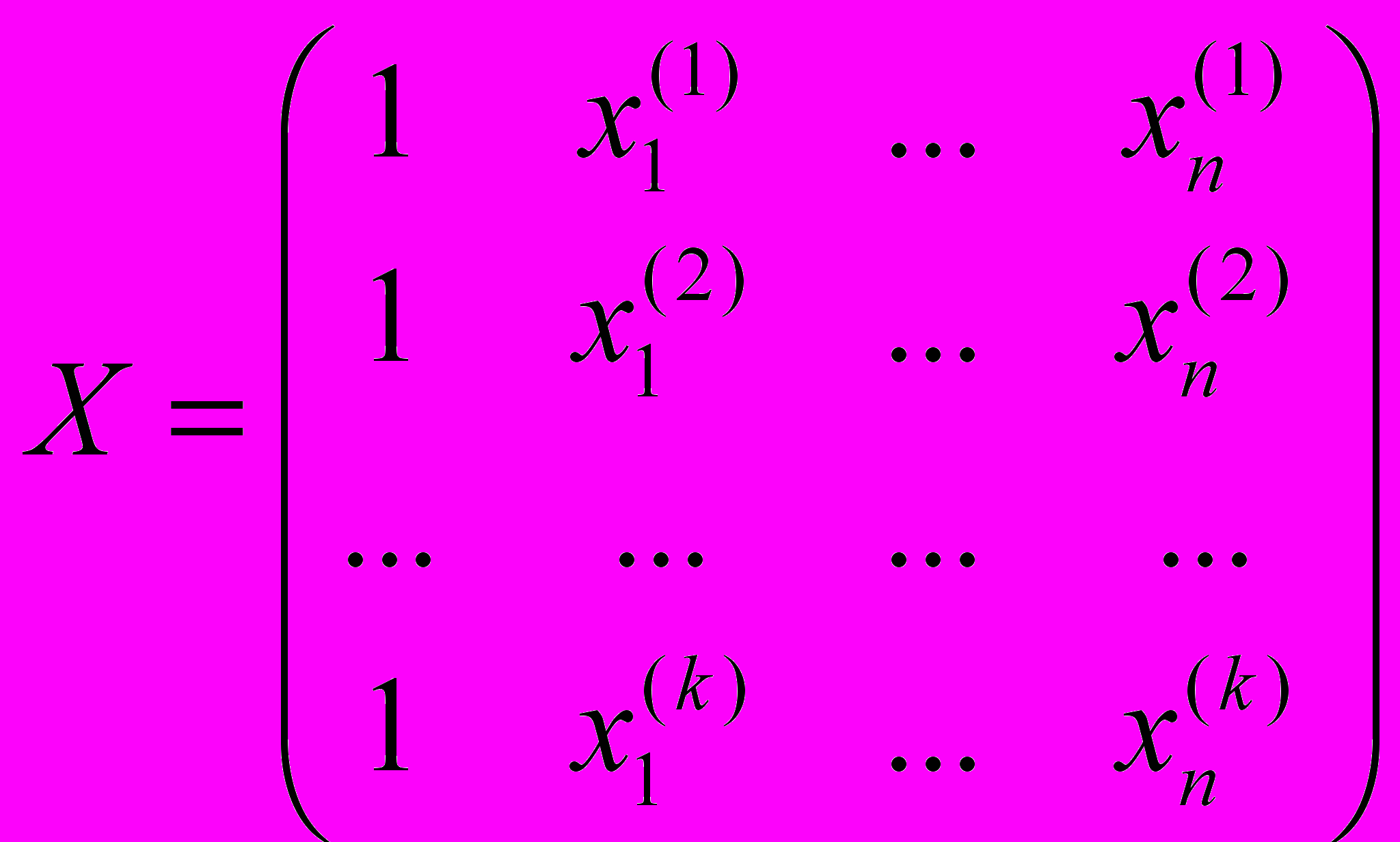, где 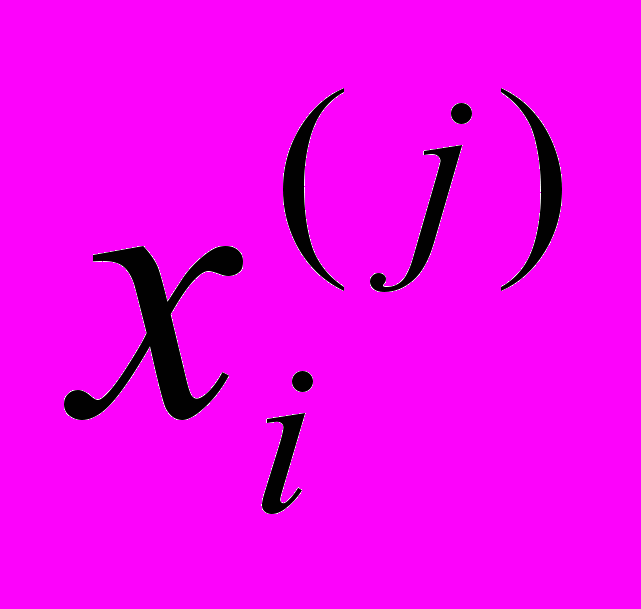– значение j-го наблюдения i-го управляющего фактора, и матрицу 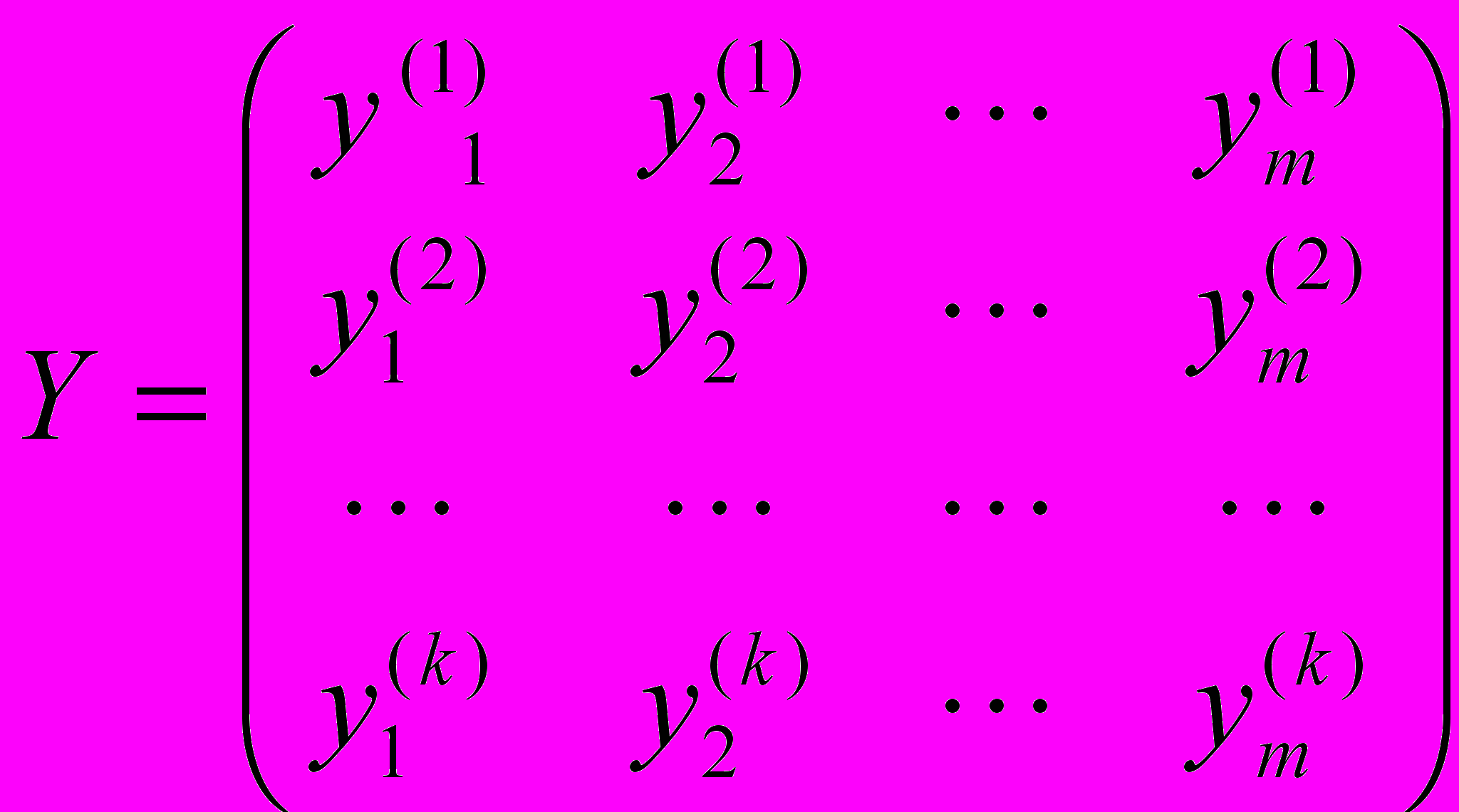, векторами которой являются реализации k наблюдений по m откликам.

Общая задача статистического исследования причинно-следственных связей между факторами и откликами может быть сформулирована следующим образом: по результатам k измерений исследуемых переменных на объектах анализируемой совокупности построить такую векторную функцию

,

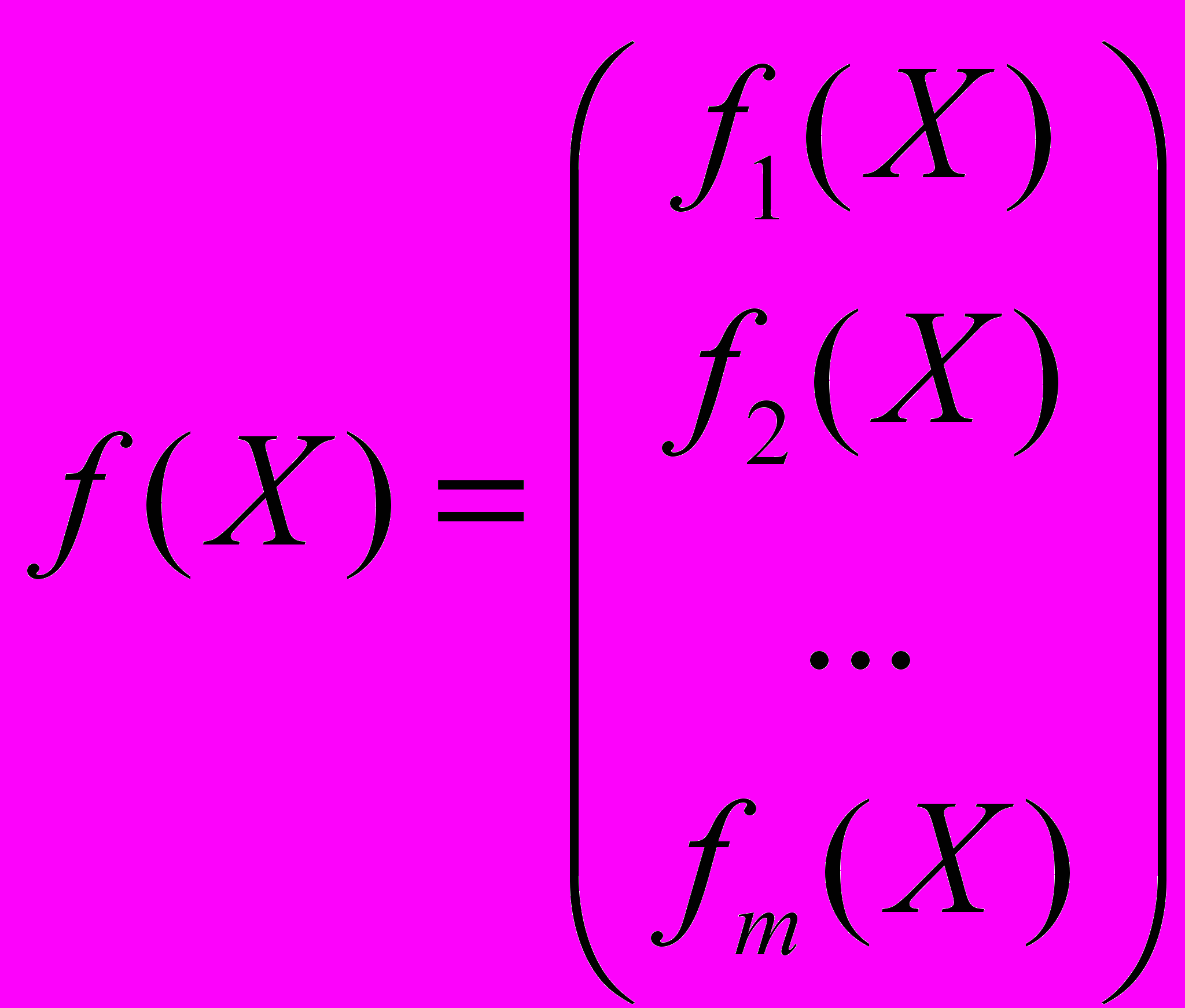которая позволила бы наилучшим (в определенном смысле) образом восстанавливать значения откликов по заданным значениям управляющих факторов. Функции вида 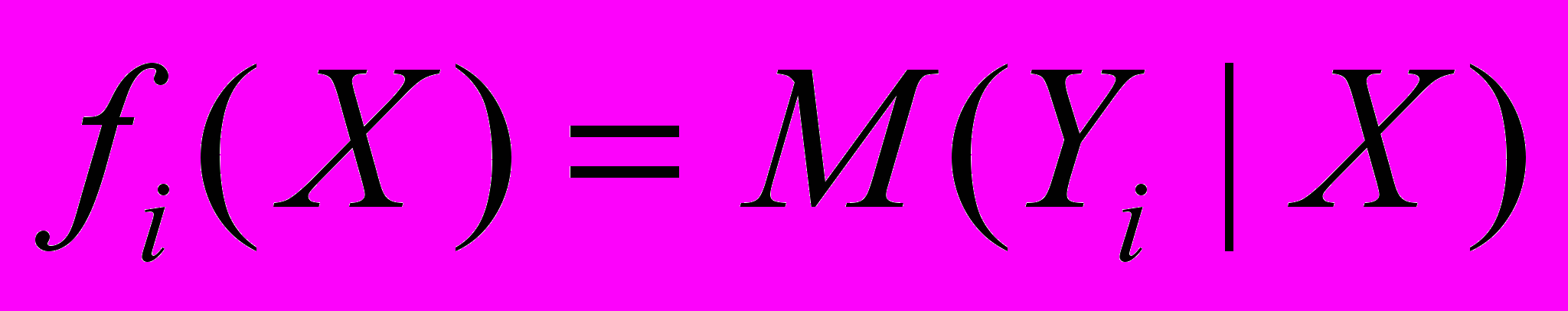, которые описывают поведение условных средних откликов, при заданных значениях управляющих факторов X и известные с точностью до значений неизвестного векторного параметра 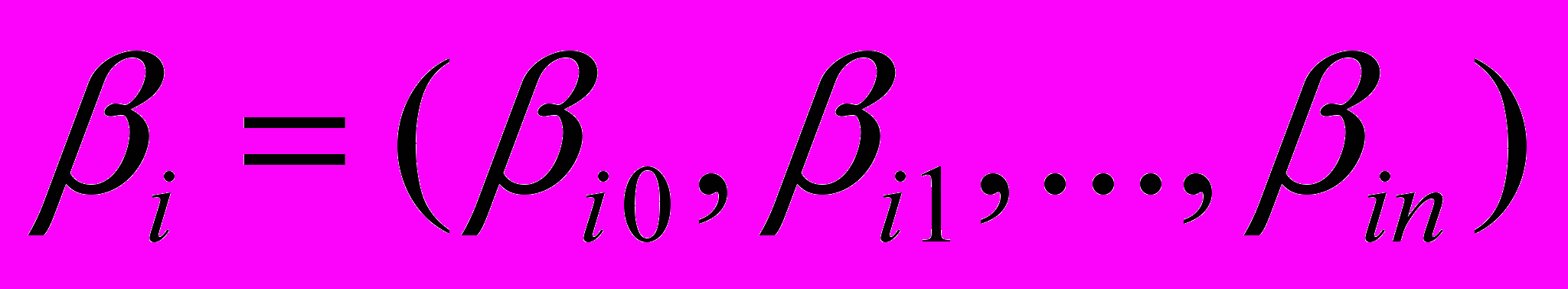, , 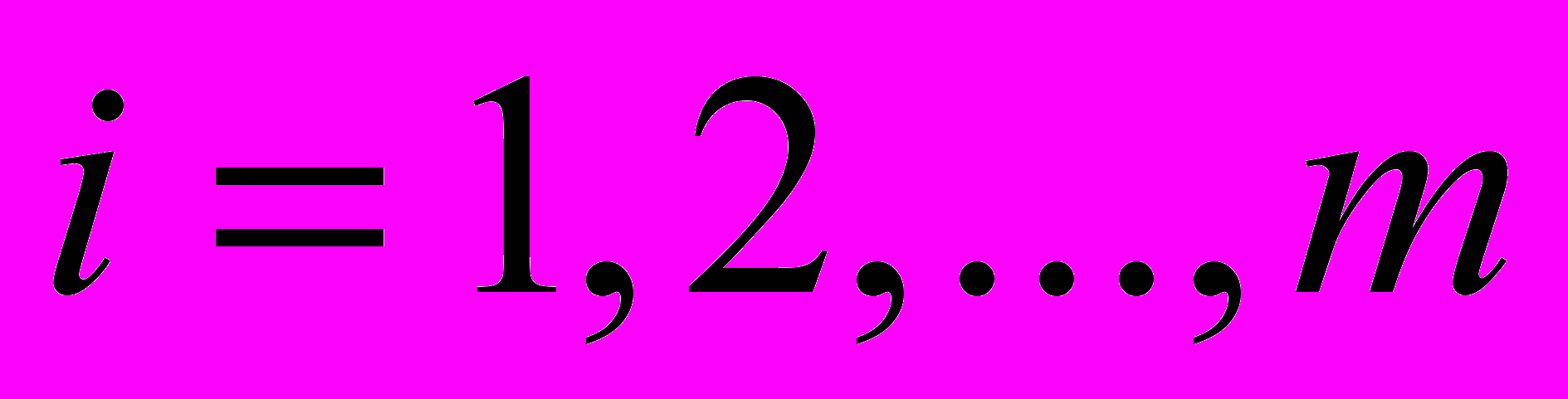называют функциями регрессии.

Будем рассматривать модель многомерной регрессии следующего вида:

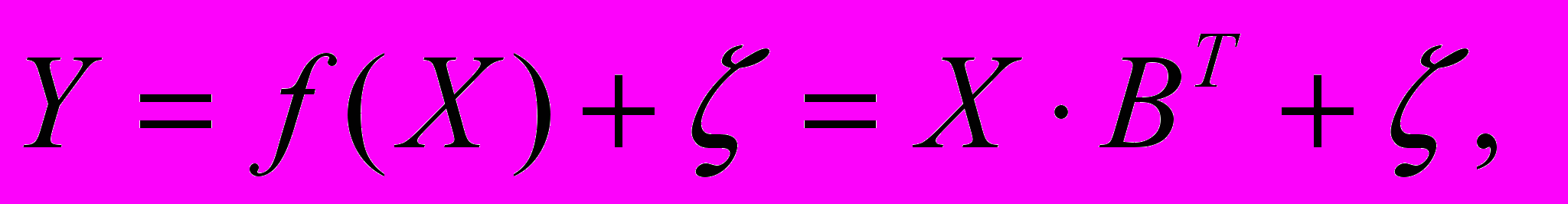(1)

где 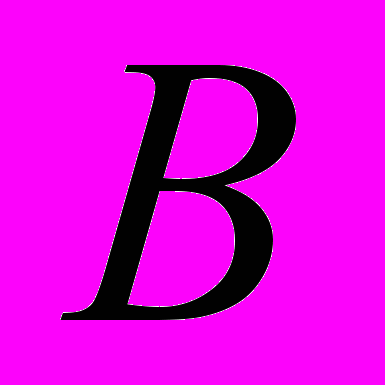– матрица параметров размерности (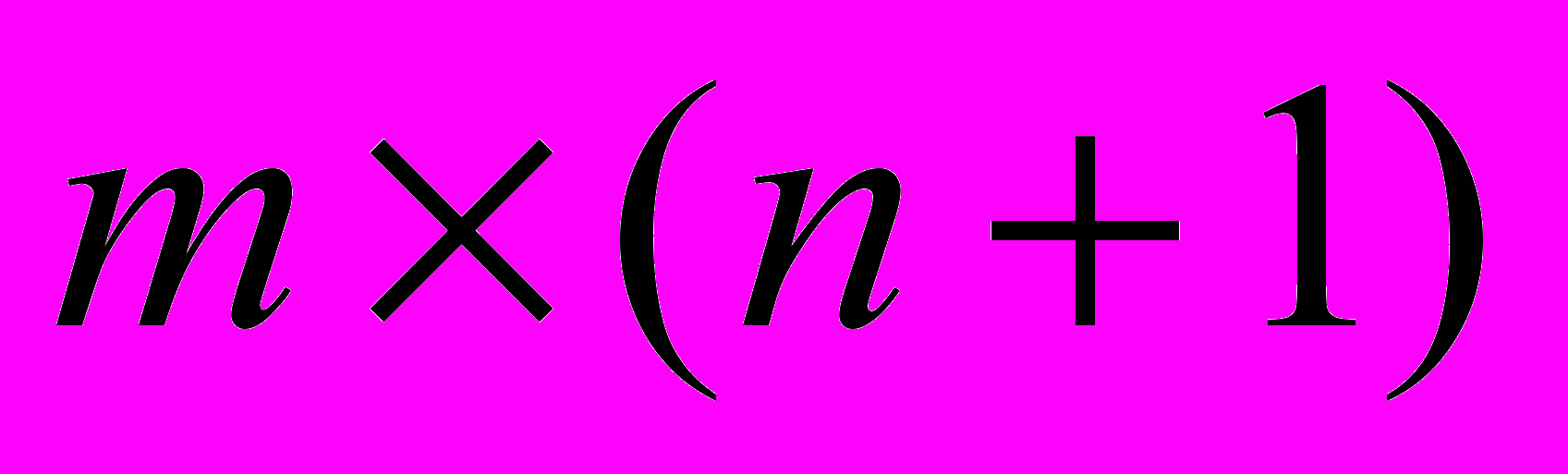), а – матрица остатков, каждый элемент 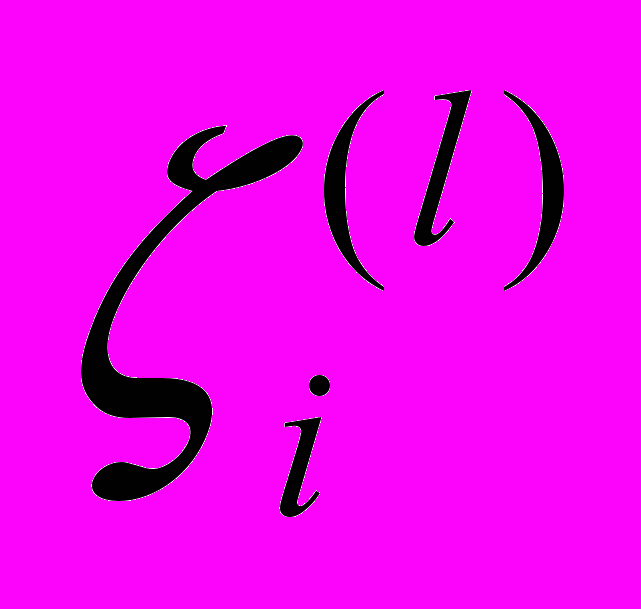, , 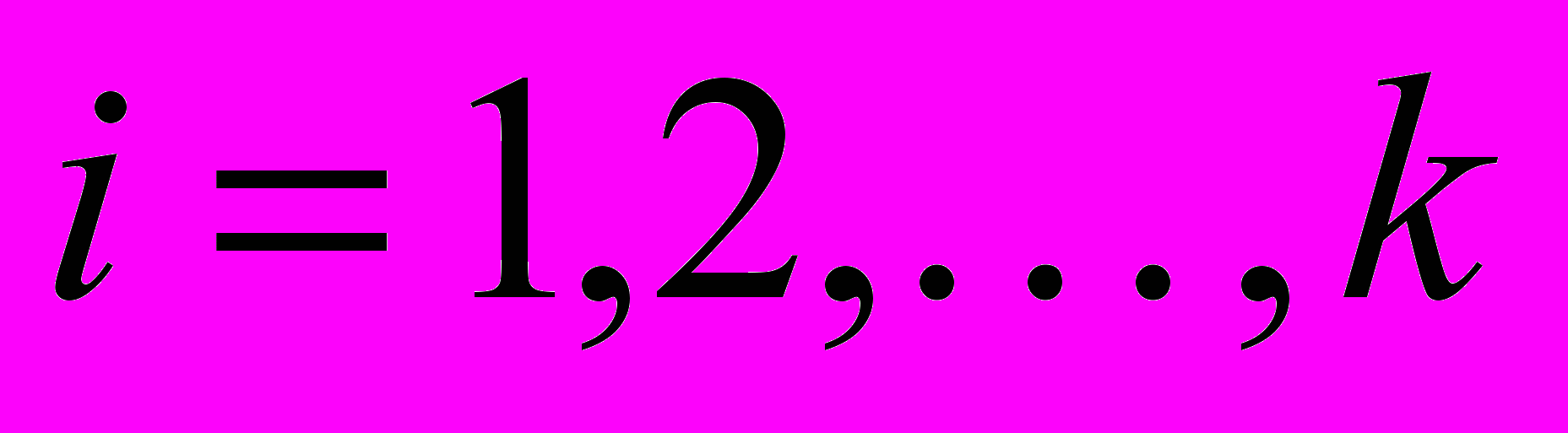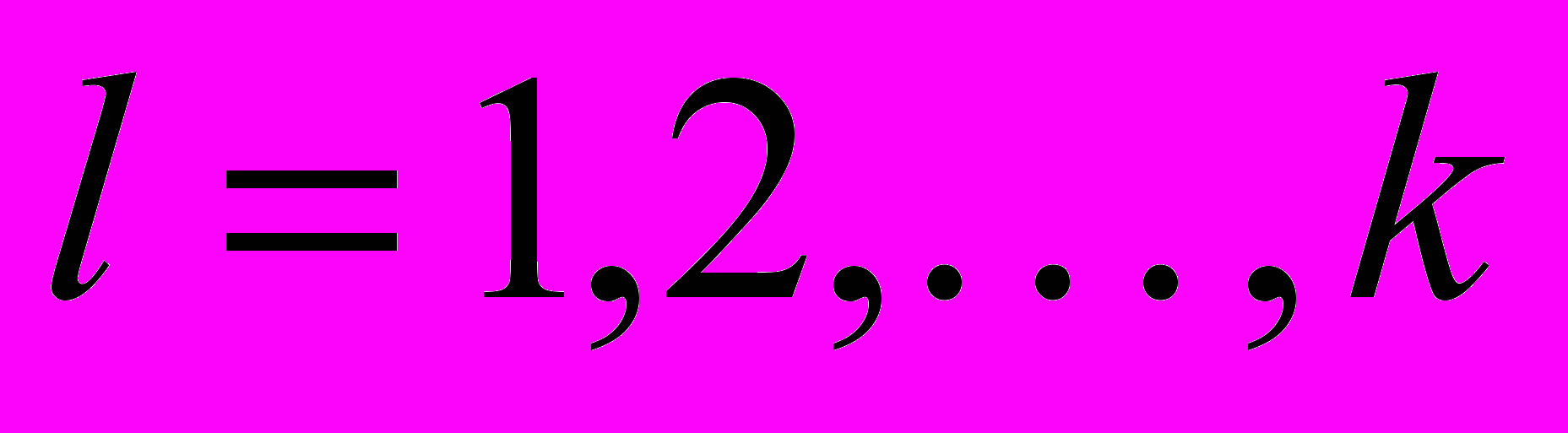которой определяет остаток в модели регрессии

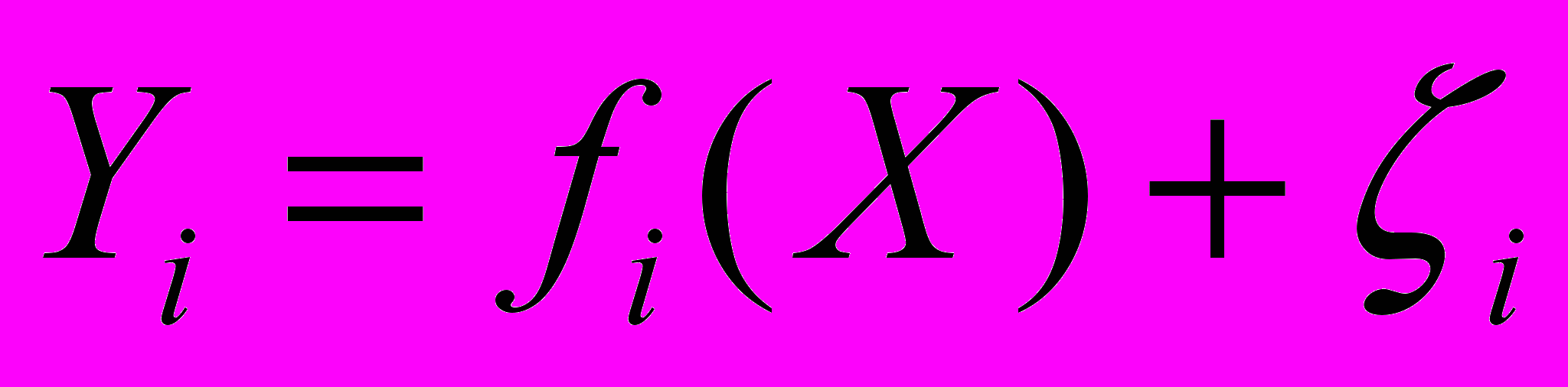(2)

для l-го наблюдения.

Исходные статистические данные

Данные, с которыми приходится иметь дело, решая задачи исследования причинно-следственных связей и прогнозирования, имеют достаточно сложную трехмерную структуру (см. рис.1). Она подразумевает наличие сложных структур взаимосвязей, которые содержатся в анализируемых массивах информации. Причем связи возникают не только между управляющими факторами и ответами, но и обнаруживаются внутри совокупности, образованной управляющими факторами (например, связанными являются такие показатели, как размер начисленных штрафов и размер взысканных штрафов). Кроме того, возможны ситуации, когда связанными являются ответы (количество обращений по поводу сердечнососудистых заболеваний и количество обращений по поводу заболеваний органов кровообращения также коррелируют между собой).

Только полный учет структуры и характера всех взаимосвязей позволяет построить модель, наиболее адекватно отражающую действительность, и, как следствие, получить наиболее эффективный инструмент управления рисками.




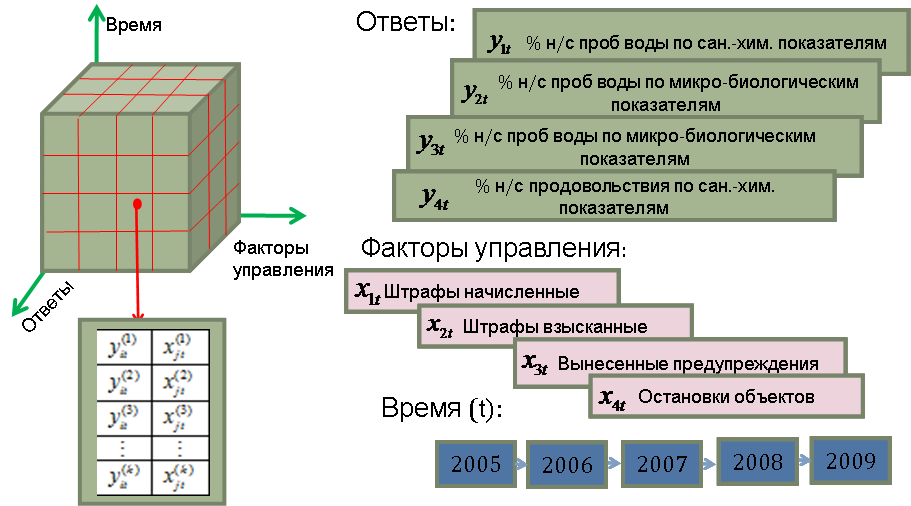
Рис. 1. Структура статистических данных

Предлагаемый метод решения задачи

В основу предлагаемого метода матричного прогнозирования рисков [3] положены следующие принципы:
  1. признание существенной многомерности анализируемой статистической информации;
  2. учет многообразия взаимосвязей между анализируемыми признаками и их структуры;
  3. Неоднородность совокупностей данных в различные периоды наблюдения.

Метод состоит из следующих этапов:
  1. Классификация наблюдений (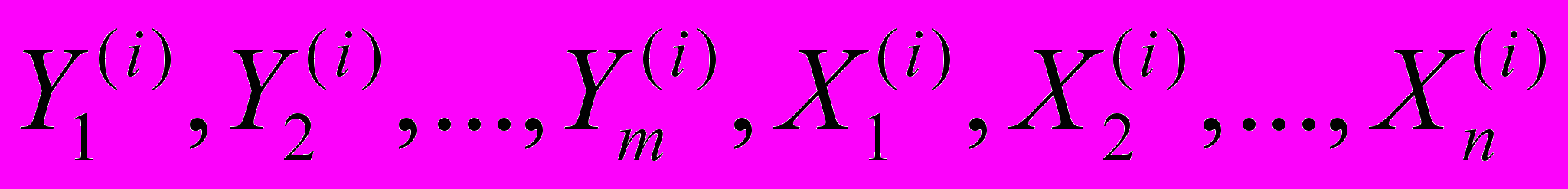), 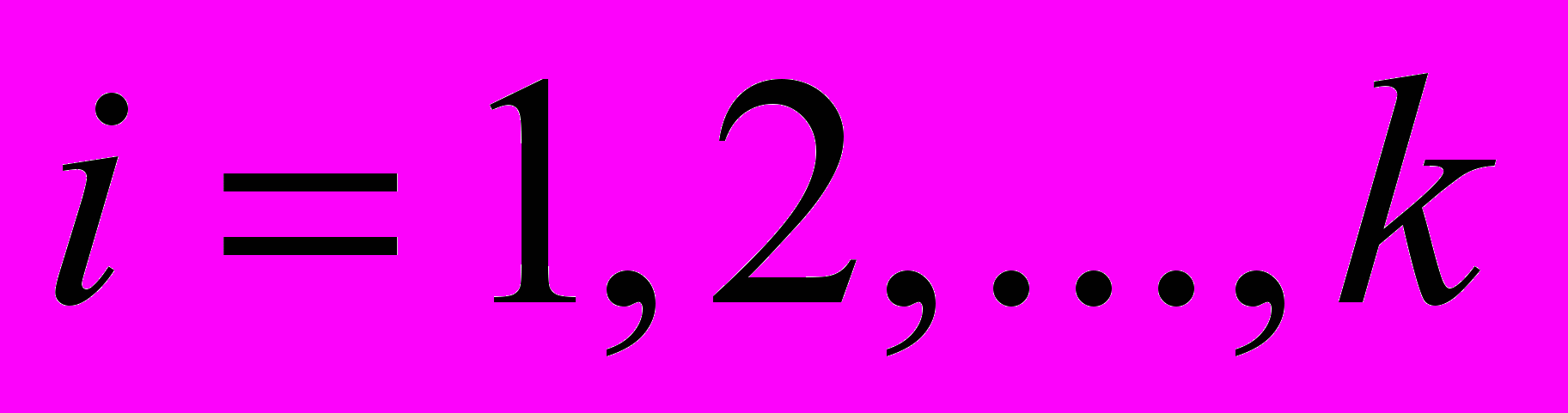на однородные группы по совокупности откликов .
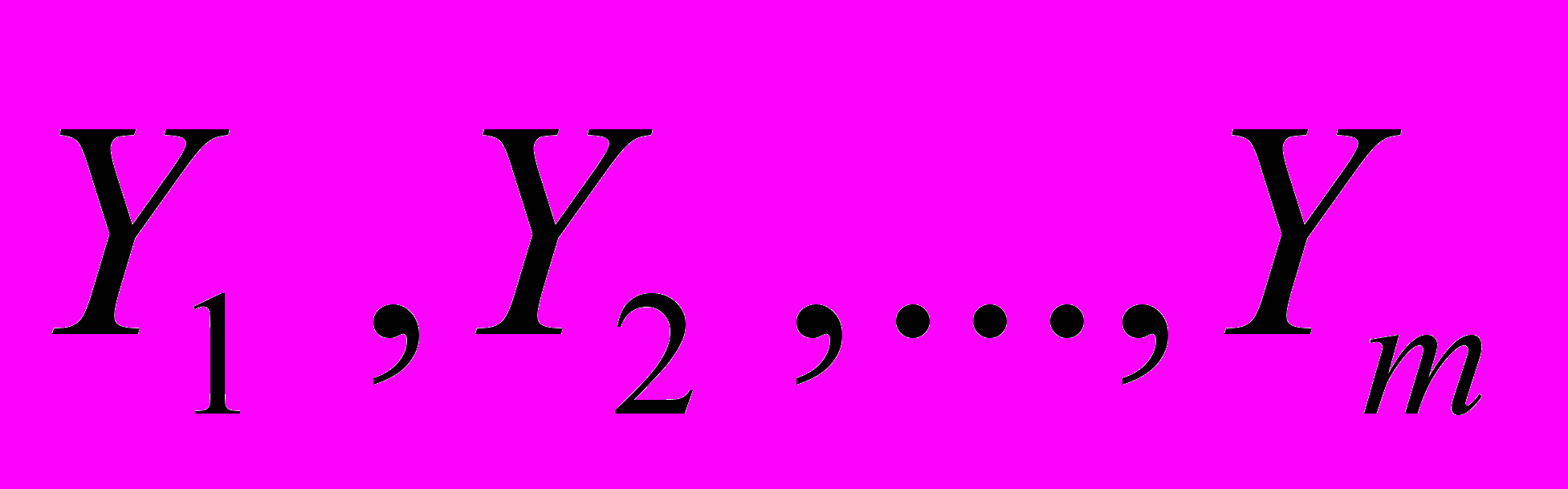  2. Исследование структуры взаимосвязей.
  3. Построение многомерных моделей регрессии.
  4. Исследование статистических свойств построенных моделей.
  5. Исследование устойчивости моделей.

Выбор наиболее значимой и устойчивой модели для каждой совокупности данных в сформированных однородных группах, позволяет осуществлять прогнозирование рисков с достаточно большой степенью достоверности.

На первом этапе применяется метод k-средних кластерного анализа, который позволяет на основании данных, содержащихся в матрице Y провести разбиение всей анализируемой совокупности на однородные группы.

Далее для каждой группы проводится анализ парной зависимости между управляющими факторами 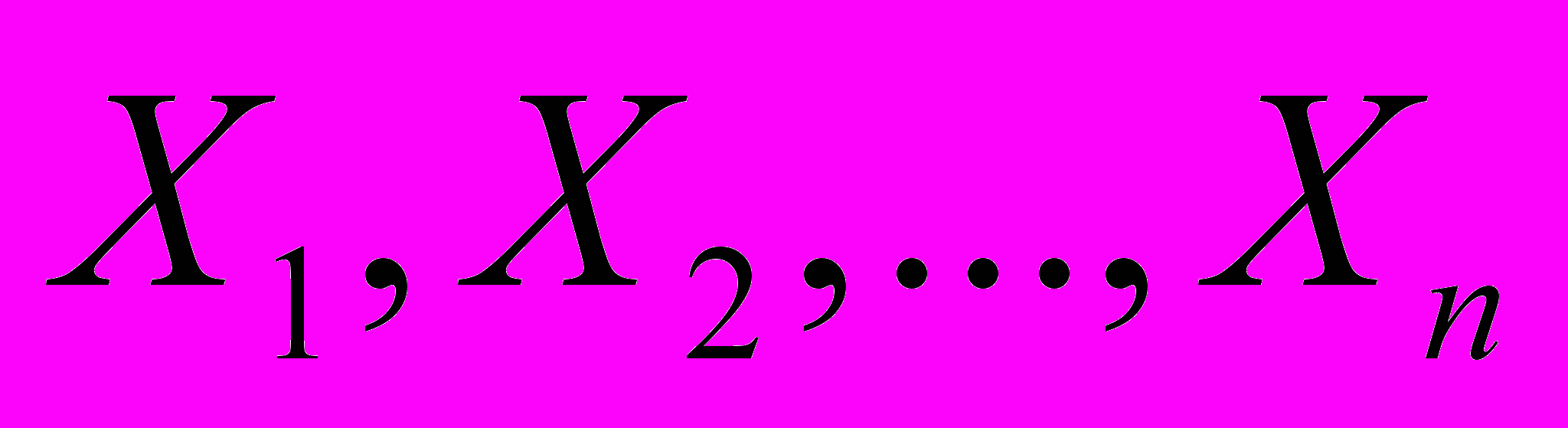с использованием коэффициента парных корреляций Пирсона [1]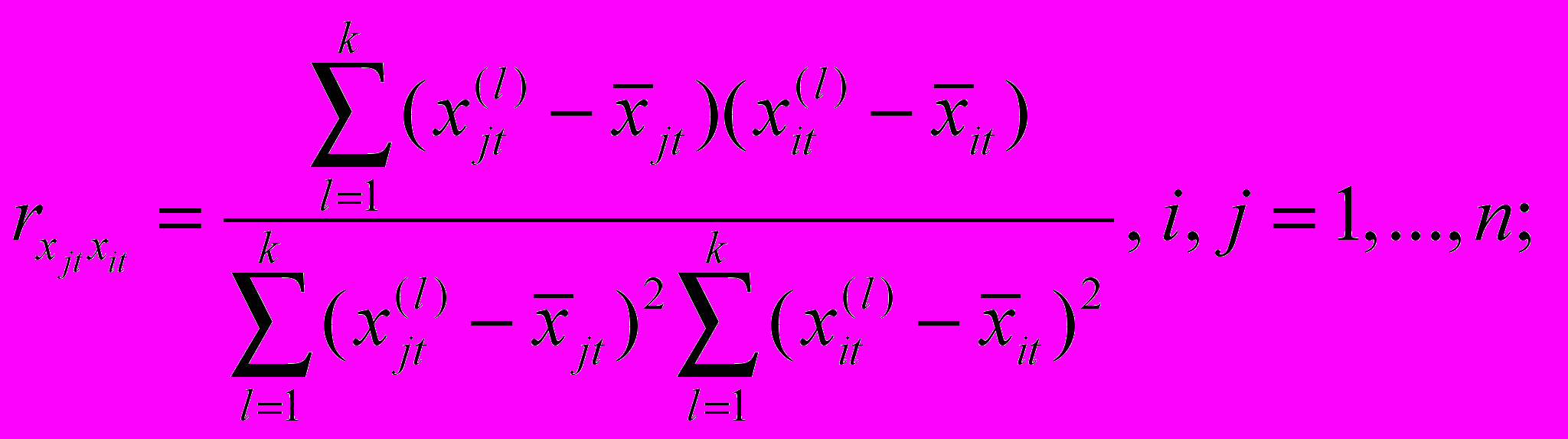



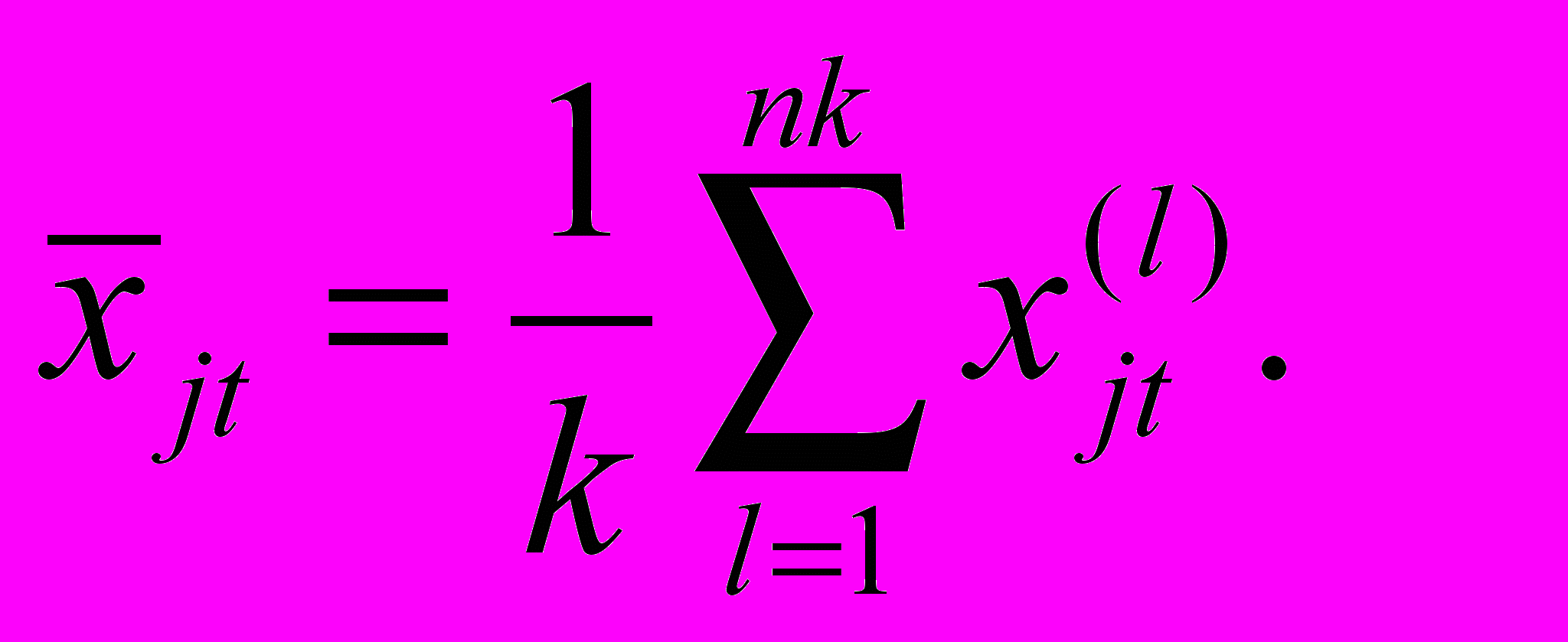
Модель (1) предполагает отсутствие линейной зависимости между управляющими факторами, поскольку ее наличие приводит к вырожденности симметричной матрицы 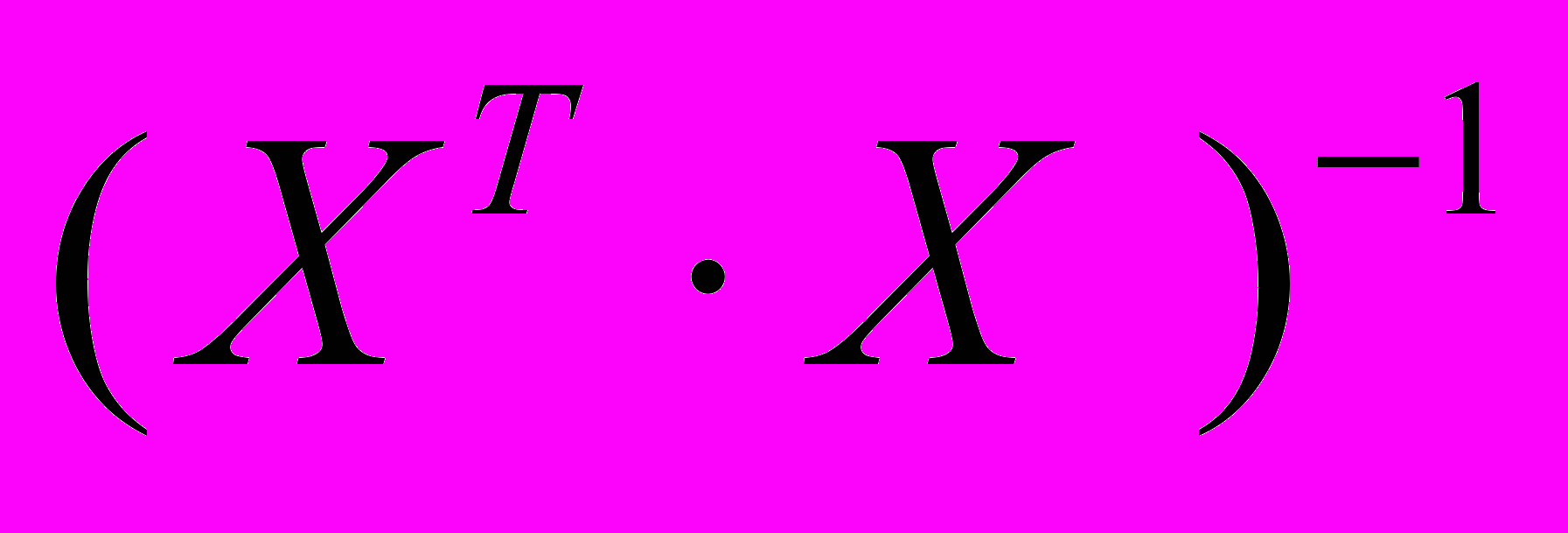. Это, в свою очередь приводит к тому, что построенная модель становится неадекватной в смысле результатов прогнозирования или результат прогнозирования будет плохо поддаваться содержательной интерпретации. В связи с этим, линейно зависимые пары разбиваются и создаются всевозможные сочетания, включающие максимальное число линейно независимых управляющих факторов. В результате может получиться N таких наборов. Каждое сочетание является основой для построения отдельной регрессионной модели вида (2).

На следующем этапе анализируется взаимосвязь между факторами управления и управляемыми факторами на основе коэффициента линейной корреляции вида

,



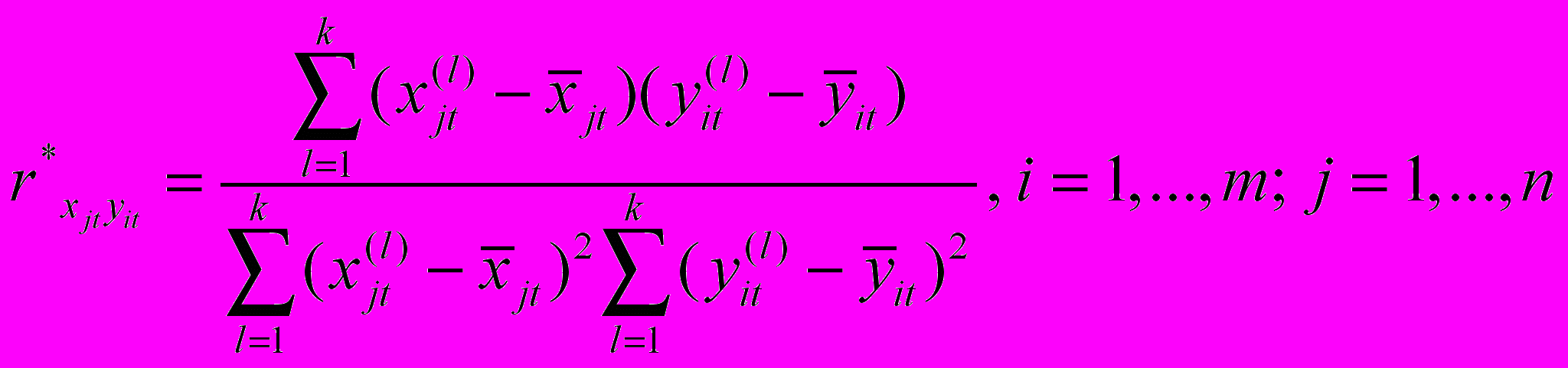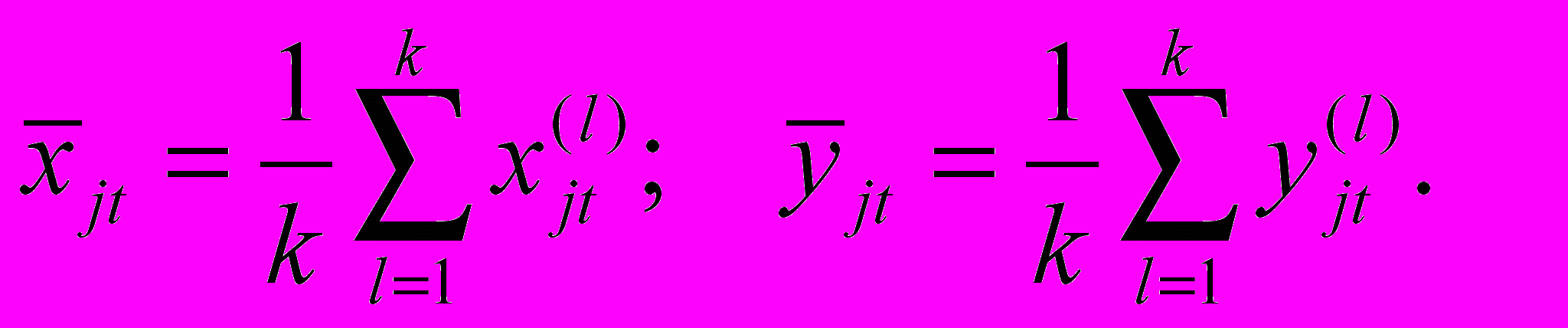
и коэффициента ранговой корреляции Спирмена по формуле

,

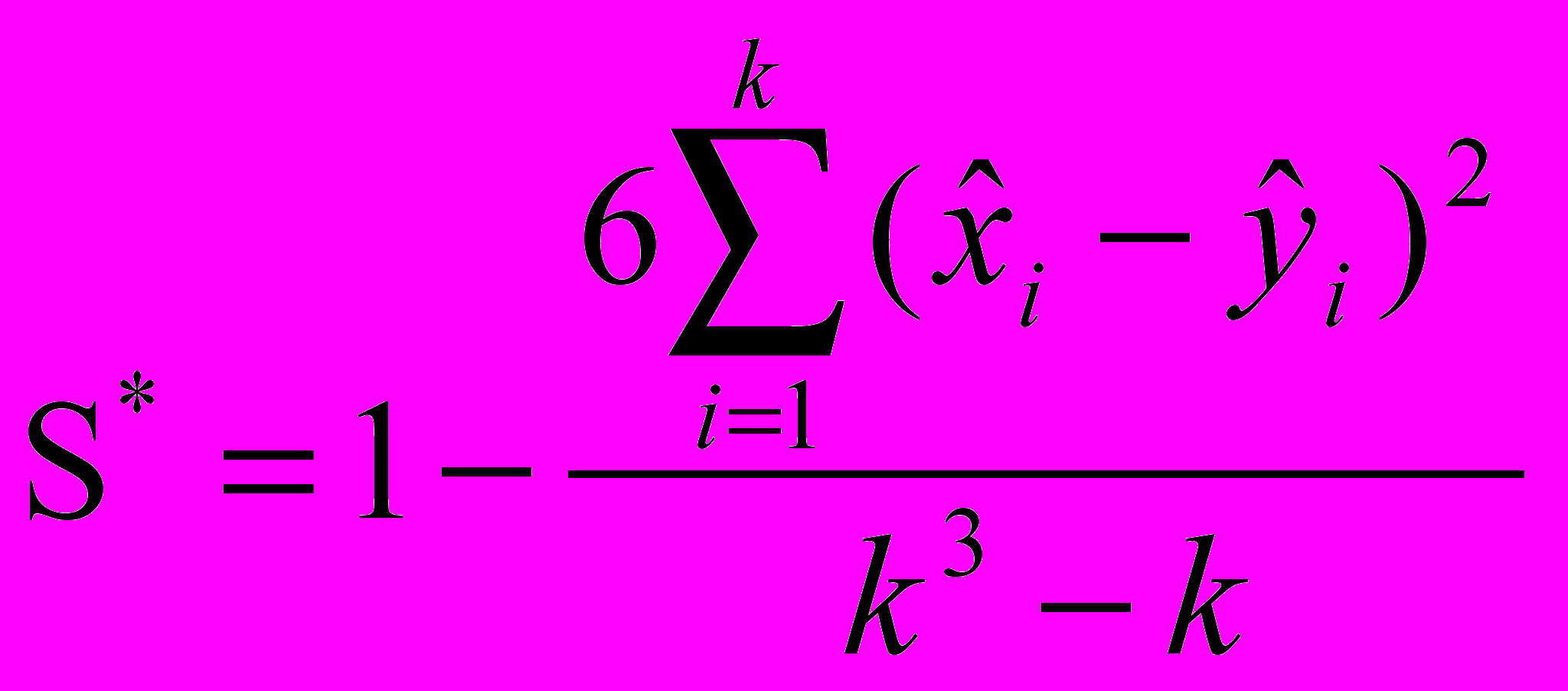где 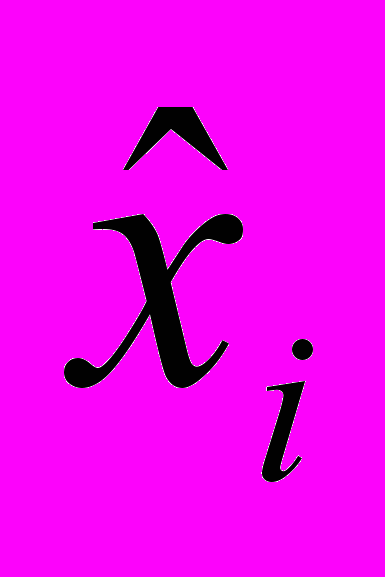, 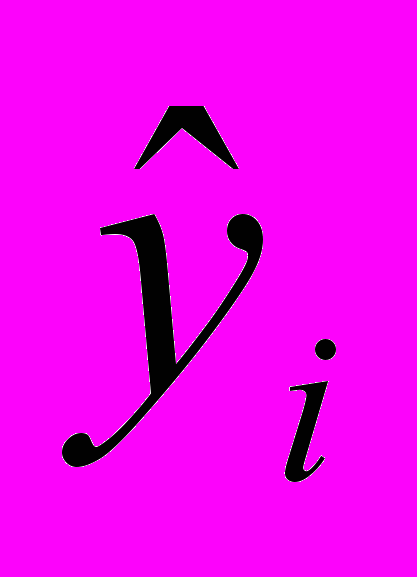– ранги соответствующих значени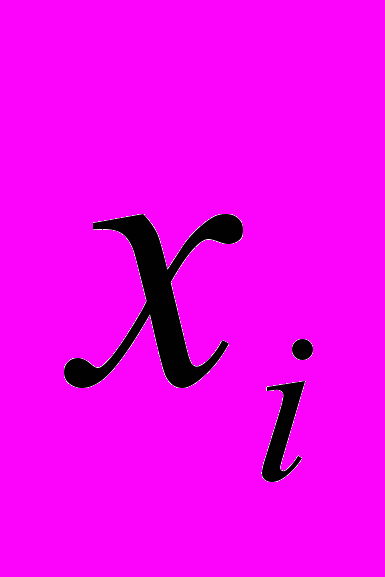й и .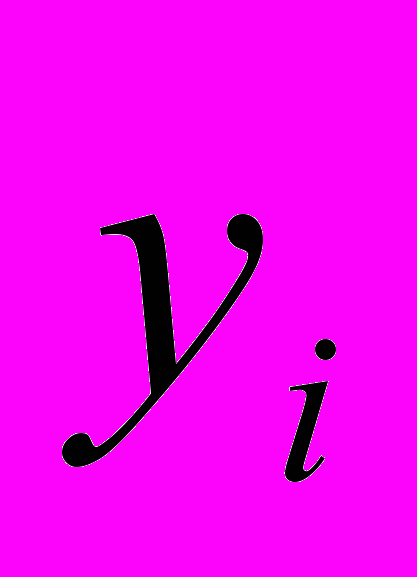

Если оба коэффициента оказываются незначимыми на уровне α=0,05, то соответствующий управляющий фактор в дальнейшем анализе не участвует. Таким образом, получаем набор «модифицированных» управляющих факторов. Обозначим такие факторы 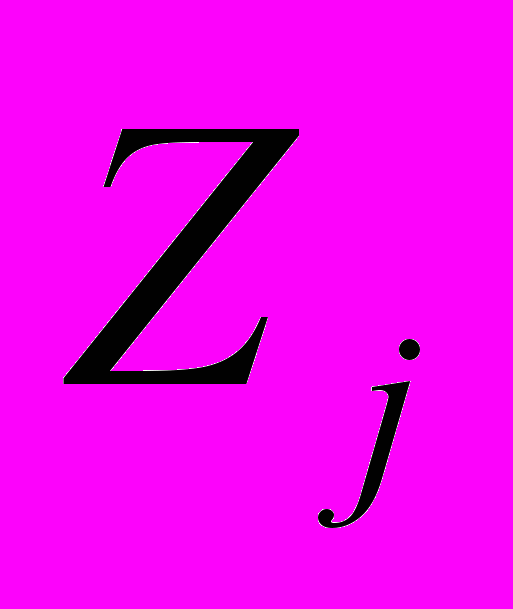(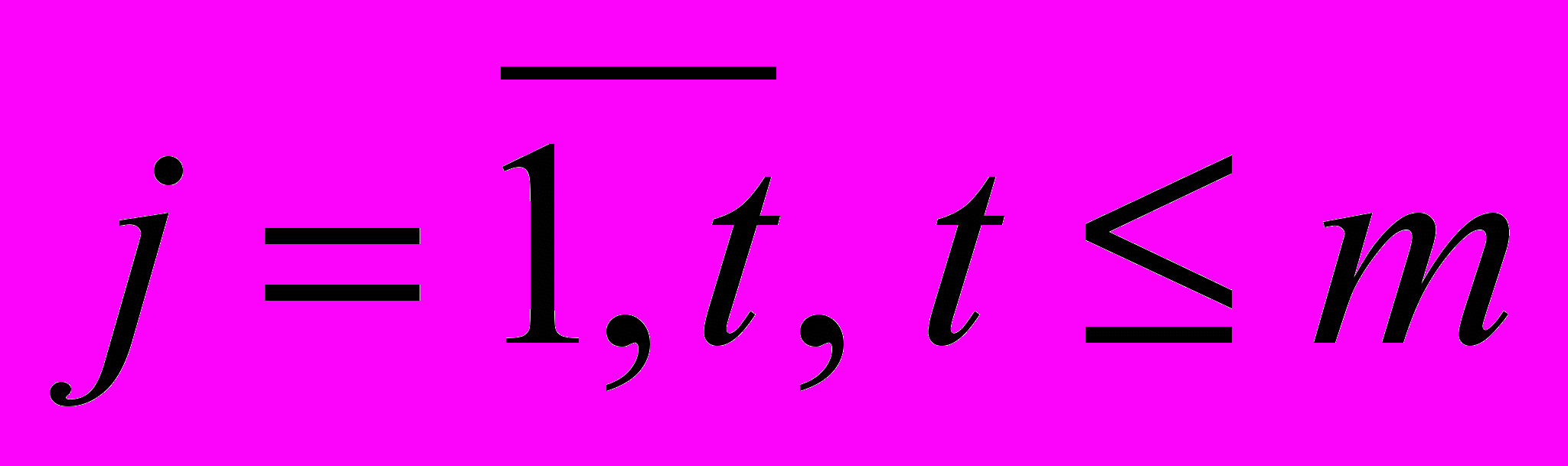) и получим «модифицированную» матрицу, содержащую k наблюдений по t управляющим факторам: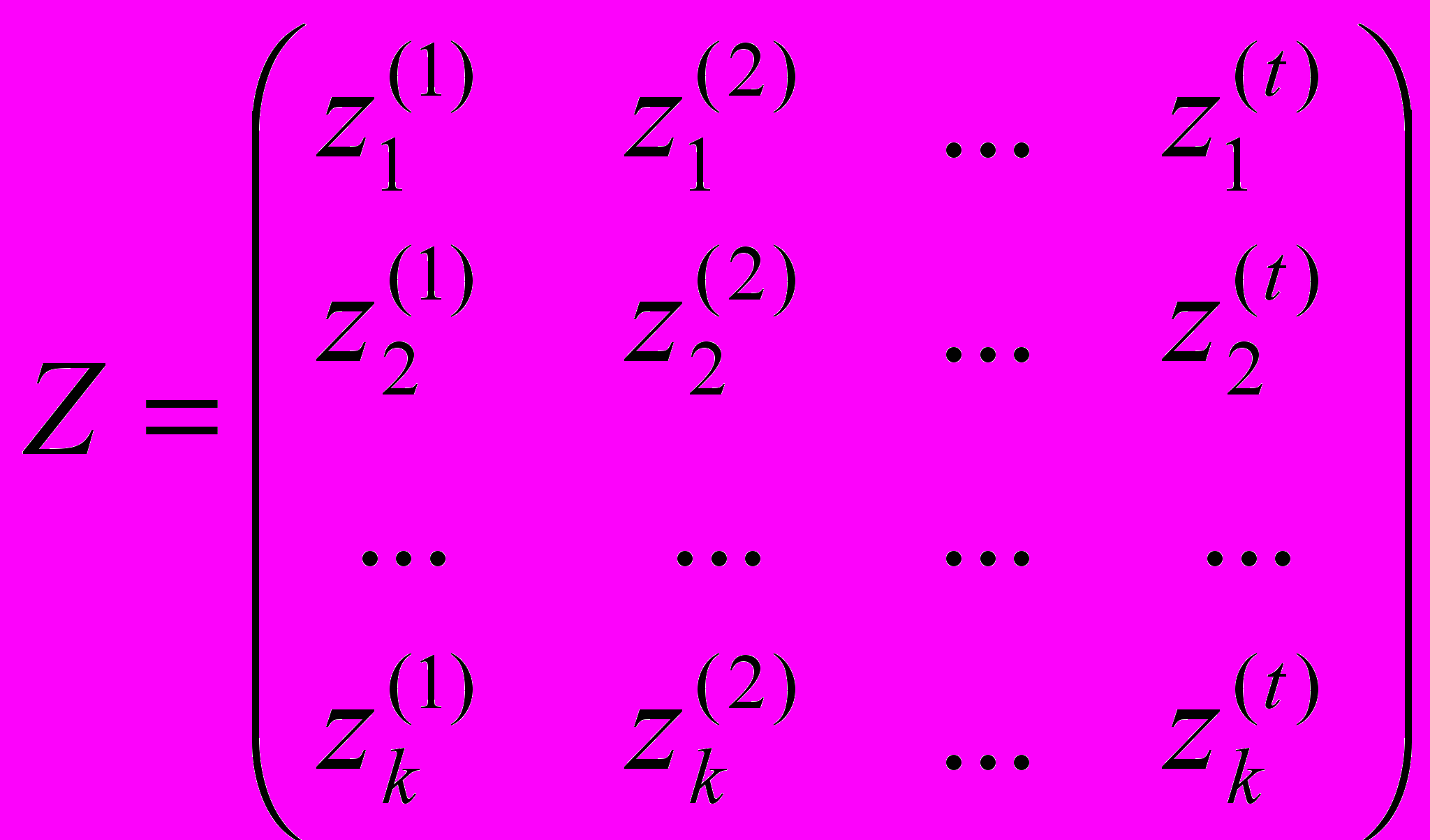



Такую процедуру необходимо проделать для каждого 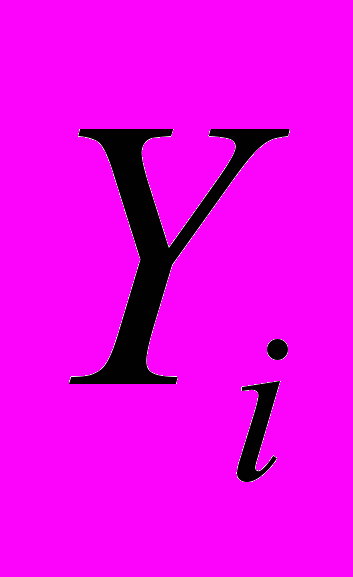, 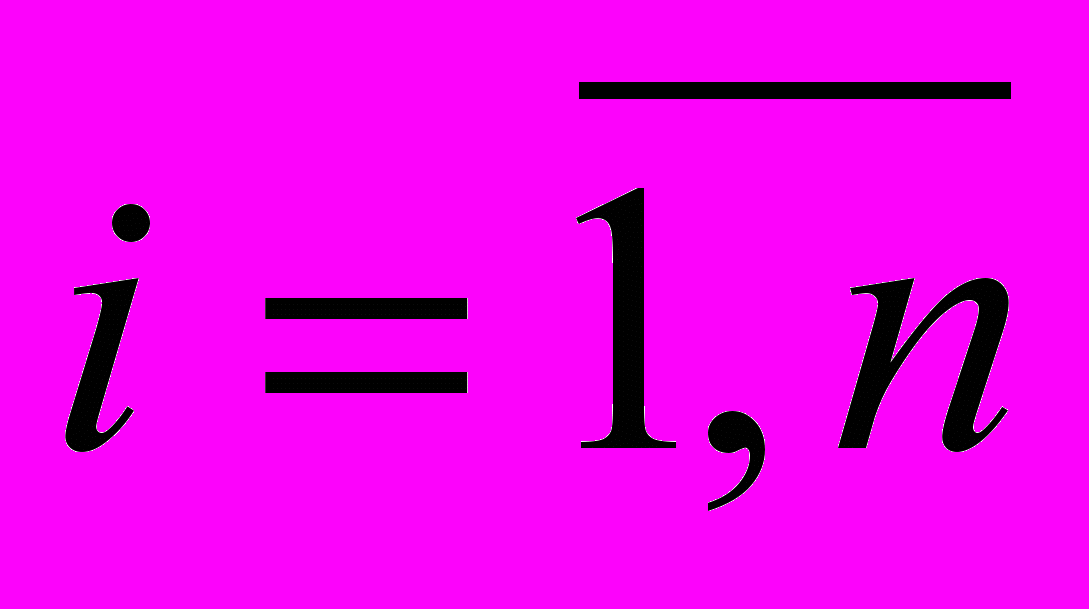. В результате получаем набор из N моделей. Для каждого набора, на следующем шаге метода строится модель многомерной регрессии вида (1), для которой затем производится проверка статистических свойств, подразумевающая:

- проверку значимости коэффициентов модели с помощью критерия Стьюдента [2];

- вычисление коэффициента детерминации,

- проверку значимости модели в целом с помощью критерия Фишера [2].

Отобрав, таким образом, все значимые модели, на следующем этапе, из них выделяются наиболее «устойчивые» к изменениям в структуре данных, возникающим с течением времени.

Анализ «устойчивости моделей» производится на основании анализа матриц B с использованием статистики амплитудного коридора [4]




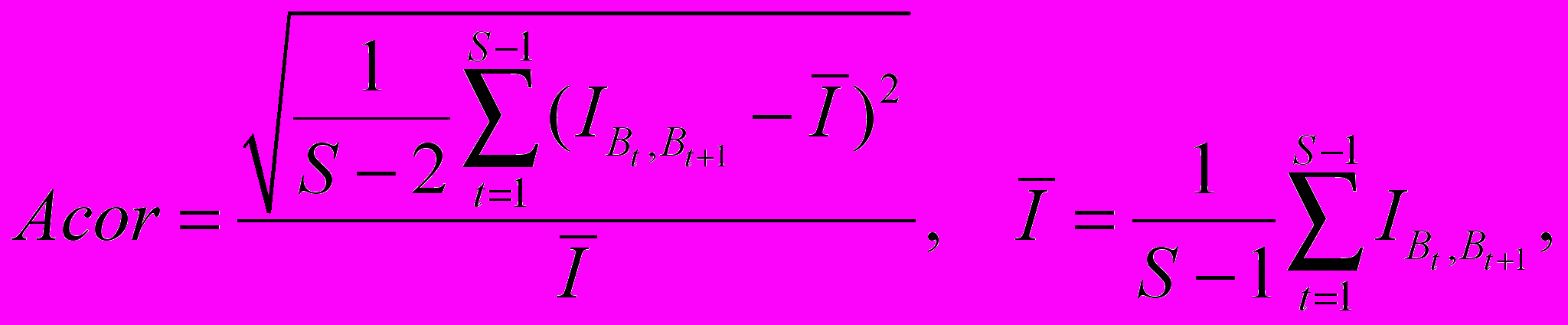
(3)

о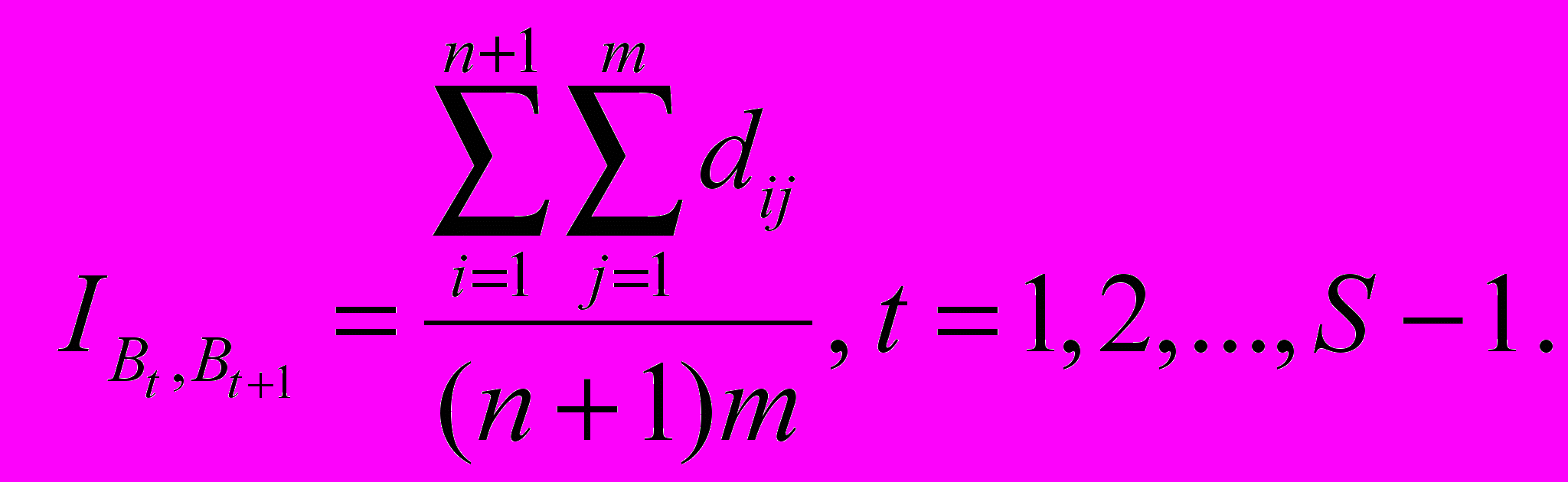снованной на информационном расстоянии между матрицам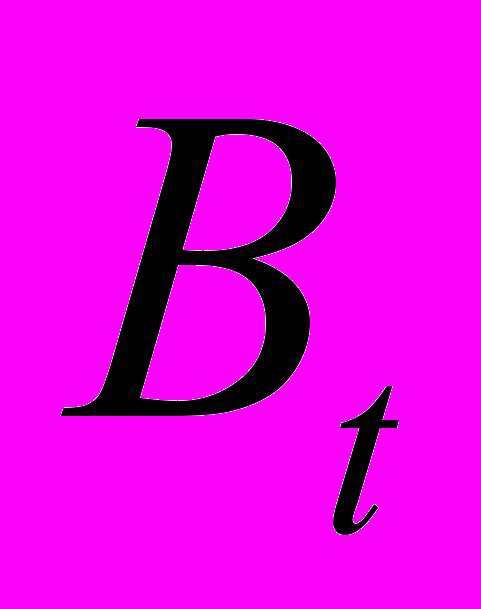и и 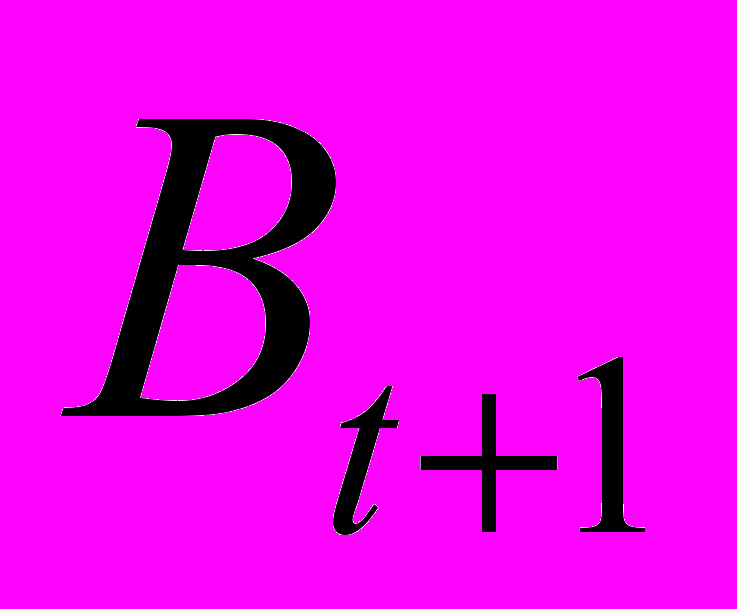коэффициентов многомерных моделей (1), рассчитанных по данным за t-ый и t+1 годы:


Здесь 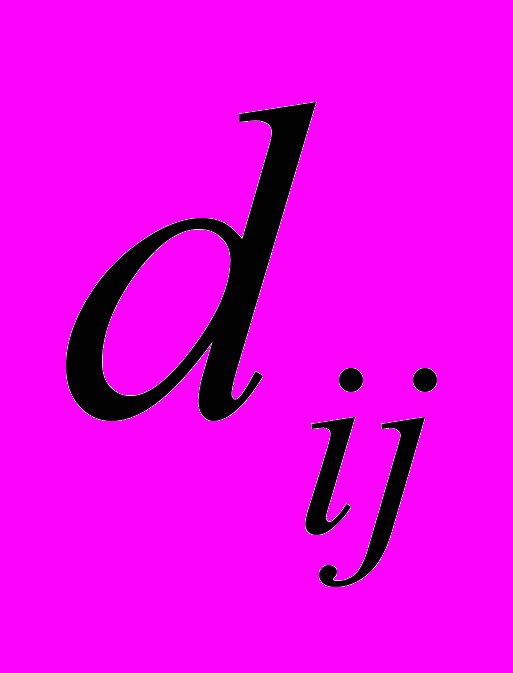– некоторая метрика, определяющая разницу между соответствующими элементами матриц 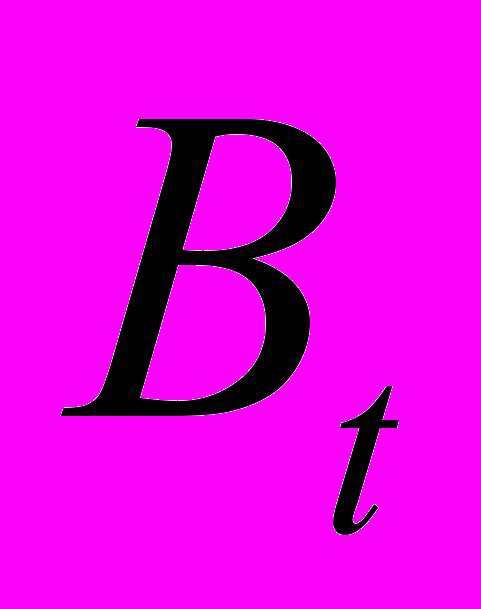и 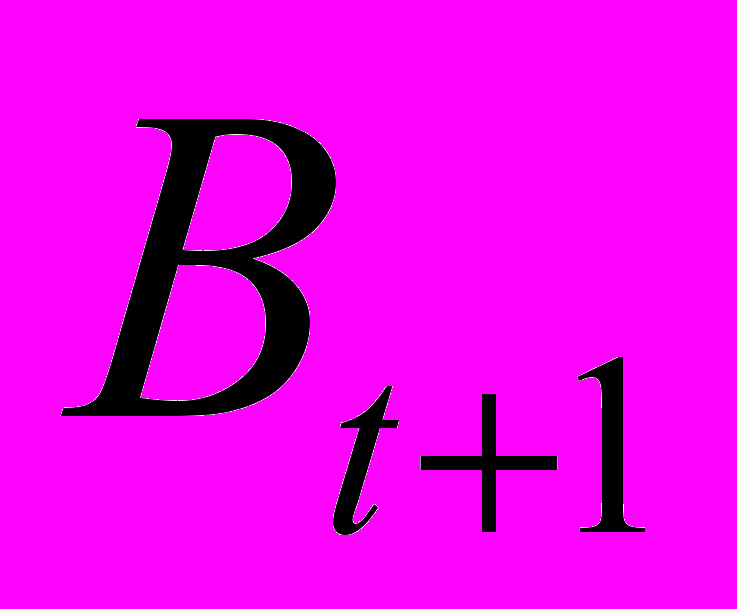, 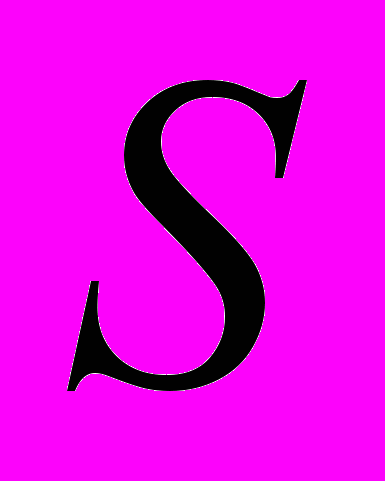– количество временных периодов, которые участвуют в анализе. Вычислив значение статистики (3) для каждой модели, отбираем лучшую модель из условия

.

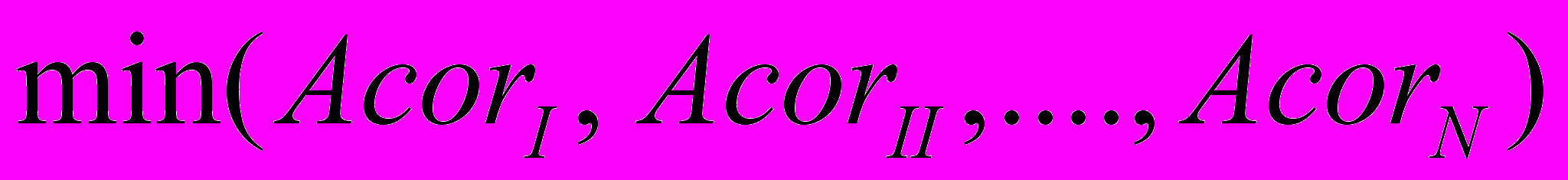Данный метод построения, анализа и отбора многомерных моделей в настоящее время положен в основу программного компонента, разрабатываемого в рамках научного проекта Федерального научного центр медико-профилактических технологий управления рисками здоровью населения [3].

Библиографический список


1. Айвазян С.А. Прикладная статистика: Исследование зависимостей/ С.А. Айвазян, И.С. Енюков, Н.Д. Мешалкин. – М.: Финансы и статистика, 1989.

2. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. «ЮНИТИ». Москва, 1998.

3. Бабушкина Е.В., Гусев А.Л., Лупач Д.Ю. Разработка базовых элементов информационно-аналитической поддержки анализа причинно-следственных связей факторов среды обитания и здоровья населения // Материалы Всероссийской науч.-практич. конф.-Кумертау, 2010.

4. Гусев А.Л., Хрущева Е.В. Выбор модели на основе сравнения аиплитудных коридоров в задачах управления рисками здоровью населения // Вестник Пермского университета: Математика. Механика. Информатика, Пермь, 2010. Вып. 3(3), С. 76-79


Modeling casual-and-effect relations in the risks analysis

Lupach D.U.

Perm State University, E-mail: lupachdu@ramber.ru


The article describes the method of construction, analysis and selection of multidimensional models for risk prediction.