Функциональный подход

Вид материала

Документы

Содержание E – единичная матрица (E Х – A Х) = Y Ковариация. Корреляция. Примеры. 11. Структурно-причинные модели. 15. Применение игровых моделей в банковской деятельности. S(n)p платёж - C = [(1+p)

Подобный материал:

• I общие основы грамматической стилистики современного испанского языка I. Функциональный, 658.42kb.
• Программно-функциональный подход к освоению нефтегазовых ресурсов новых регионов, 652.64kb.
• Программа дисциплины «Информационные технологии в анализе инвестиционных проектов», 132.21kb.
• Статистики Российской Федерации Заместитель начальника Управления национальных счетов, 104.36kb.
• Формирование социально-культурной активности личности в учреждениях культуры и образования:, 780.45kb.
• Лекция 12. По теме: Системный и функциональный подход к управлению банкротством, 134.7kb.
• Содержание программы: Функциональный и процессный подход к построению системы уп цели, 40.27kb.
• Программа кандидатского экзамена по специальности 01. 01. 01 Вещественный, комплексный, 118.98kb.
• Темы и их краткое содержание Тема I. Возникновение массовых коммуникаций в обществе:, 47.98kb.
• Программа курса основы нового управления (психологический аспект), 401.34kb.

1. Функциональный подход: рассматривается взаимодействие объектов системы при выполнении ими определенных функций.

Любые объекты можно рассматривать во взаимодействии.


Х = АK^αL^βM^γe^∆t, где α, β, γ – коэффициенты эластичности,

∆t – фактор НТП

dL / dt ≈ λL – уравнение динамики трудовых ресурсов


L₁ = L₀℮^λt

λ= (β – α) - разность между рождаемостью и смертностью

dK / dt = I

K_t+1 = dK / dt – K₀

5. Модель межотраслевого баланса

Х = A Х + Y (1) – матричное представление модели МОБ

E Х = Х, где E – единичная матрица

(E Х – A Х) = Y

(E – A)Х = Y

Умножим на (E – A)^-1 и получим:

(E – A)^-1 (E – A)Х = (E – A)^-1 Y

Х = (E – A)^-1 Y => Х = В Y (2), где B – матрица полных затрат

Формула (2) используется в экономике для анализа, прогнозирования и планирования.

(E – A)^-1 = 1/(E – A) = 1 + A + A² + … + Aⁿ

6. Применение МОБ для оценки структурных изменений в экономике, для оценки влияния инфляции и внешнеэкономической деятельности

Если мы рассматриваем состояние экономики во времени, то в этом случае (1) преобразуется в (2).


Х(t) = A(t) Х(t) + Y(t) (2)

В случае матрицы полных затрат: Х(t) = В(t) Y(t) (3)


Хt₁ – Хt₀ = Вt₁ Yt₁ – Вt₀ Yt₀ = Вt₁ Yt₁ – Вt₀ Yt₁ + Вt₀ Yt₁ – Вt₀ Yt₀ = (Вt₁ – Вt₀) Yt₁ + (Yt₁ – Yt₀) Вt₀

∆ Хt = ∆ Вt Yt₁ + ∆ Yt Вt₀

(Вt₁ – Вt₀) – структурные изменения в экономике,

(Yt₁ – Yt₀) – изменение конечного потребления.


Влияние инфляции


Х = A Х + Y

X_i = ∑ a_ij x_j + Y_i

j

X_i p_i = ∑ a_ij x_j p_j + Y_i p_i (*)

j

p_i / p_j – индексы цен


Внешнеэкономическая деятельность


Х = ВY

Y* = Y₁ + Y₂ , где Y₂ – экспорт

Y* = Y₂ = æY, где æ – доля экспорта в ВВП


7. Отсюда, из формулы Х = ВY, несложно определить Х*, а именно Х* = ВY*.

эконометрическую модель зависимости текущей и форвардной цен на валюту можно представить следующим образом:

p_{t + 1} = a₀ + a₁ f_t + ε_t+1,

Потребительская функция:

C_t = a₀ + a₁ Y_t + ε_t(C), 0 < a₁< t;

Инвестиционная функция:

I_t = b₀ + b₁ Y_t + b₂ r_t + b₃ K_t-1 + ε_t(I);

Монетарная функция:

M_t = C₀ + C₁ Y_t + C₂ r_t + ε_t(M);

Производственная функция:

Y_t = d₀ K_t^d1 L_t^d2 ε_t(Y);

Инфляционная функция

dln p_t = k₀ + k₁ dln w_t + ε_t(p);

Функция динамики заработной платы:

dln w_t = l₀ + l₁ dln p_t + l₂ dln Y_t + l₃ / U_t + ε_t(w);

Балансовые тождества:

Y_t = C_t + I_t + G_t;

U_t = N_t – L_t;

K_t = K_t-1 + I_t.


8. Линейная регрессионная модель: простая регрессия, модель множественной регрессии.

y = f(x; a) + ε (1 Простая регрессия


Примером модели (2) является модель макроэкономики, отражающая закон А.Оукена об обратной зависимости темпа роста ВНП от темпа роста уровня безработицы:

∆ Y_t / Y_t = ã₀ + ã₁ * ∆ U_t / U_t,


y = f(x_1, x_{2, …,} x_m; a) + ε Модель множественной регрессии

y = f(x; a) + ε (1); МНК

y = a₀ + a₁x + ε (2).


9, Моменты.

_N

Момент k-го порядка: M = ∑(X_i - A)^k / N

<sub>i=1

N</sub>

1. A = 0, k = 1, => M[X] = 1/N*∑X_i – момент первого порядка;
   

<sub>i=1

N</sub>

2. A = M[X], k = 2, => D[X] = ∑(X_i - M[X])² / N – центральный момент второго порядка
   

_i=1 (дисперсия);

_N

3. A = M[X], k = 3, => S[X] = ∑(X_i - M[X])³ / N – центральный момент третьего порядка
   

_i=1 (асимметрия);


Ковариация. Корреляция. Примеры.


ковариацией и вычисляется по формулам:

cov_xy = ∑ (X_i – M[X])(Y_i – M[Y]) / (N – 1) = σ_xy,


коэффициент корреляции:

ρ_xy = σ_xy / σ_x σ_y, где σ_x = cov_xx, σ_y = cov_yy.


коэффициент детерминации для оценки адекватности регрессионной модели.

R² = ∑(y_i^ф– M[y_i])² / ∑(y_i^р– M[y_i])²,


10, Лаговые модели.

y_t = a_t + b₀x_t + b₁x_{t - 1} + … + ε_t = a_t + ∑ b_k x_{t - k} + ε_t.

_k=0

∞

∑ b_k = b < ∞, а, следовательно, lim b_{k = 0}


11. Структурно-причинные модели.

y₁ = b₂₁ y₂ + c₁₁x₁+ c₂₁x₂+ ε₁ (c₁₁ = 1),

y₂ = b₁₂ y₁ + c₁₂x₁+ c₃₂x₃+ ε₂ (c₁₂ = 1),



12, Игровые модели в экономике

α = max α_i = max min a_ij – нижняя чистая цена

i i j


β = min βj = min max a_ij – верхняя чистая цена

j j i


Критерий Вальда.

α = max α_i = max min a_ij (i = 1…m; j = 1…n).

i i j


Критерий Сэвиджа

r_ij = max a_ij - a_ij (i = 1…m; j = 1…n),

i


S = min S_i = min max r_ij.

i i j

Критерий Гурвица


ā_i = γ min a_ij + (1- γ) max a_ij (0≤ γ ≤1);

j j

15. Применение игровых моделей в банковской деятельности.

критерием Байеса:

_n

a_i* = max ∑q_j a_ij.

_{j = 1}

критерием Вальда: a_i* = max min a_ij (i, j = 1,n),

критерием Сэвиджа: r_i* = min max r_ij.

i j


16, Моделирование финансовых операций.

S_t = S₀(1+p_tt)

p_t = (S_t - S₀) / S₀

S_t = S₀ + S₀p_tt + S₀p_tt + … + S₀p_tt = S₀(1+p_tt)

d_t = (S_t – S₀)/S_t, где d_t - дисконт или учётная ставка

S_t – S₀ = S_t*d_t

S_t – S_t*d_t = S₀

S_t(1- d_t) = S₀

S_t/S₀ * (1- d_t)/S₀ = 1

S_t/S₀ = S₀/(1- d_t)

p_t = S_t/S₀ – 1 = 1/(1- d_t) – 1 = d_t/(1- d_t)

S₁ = S₀ + S₀p_t= S₀(1+p_t)

S₂ = S₁ + S₁p_t= S₁(1+p_t) = S₀(1+p_t)²

S₃ = S₀(1+p_t)³

S_t = S₀(1+p₁t₁+p₂t₂+…+p_nt_n) = S₀(1 + ∑ p_it_i) наращивание перв суммы

ⁱ⁼¹

_n

S_t = S₀(1+p₁t₁)(1+p₂t₂) …(1+p_nt_n) = S₀∑ (1 + p_it_i)

ⁱ⁼¹

17,18 Постоянные финансовые ренты. Дисконтирование финансовых рент.

S₀ = S_t/(1+ p_t)^t

_{n n}

S(t) = S(n) = ∑C(1+p)^n-k = C∑ (1+p)^n-k (1) периодический платеж.

^{k=1 k=1}

(1+p)ⁿ – 1 геометр прогрессия

S(n) = C p


ln [C + p S(n)] – ln C

срок накопления S(n) - n = ln (1+p)

S(n)p

платёж - C = [(1+p)ⁿ – 1


C[(1+p)ⁿ - 1]

процентная ставка - p = S(n)


_n C

=> S(0) = ∑ (1+p)^k (6)

^k=1

C [1 - (1+p)^-n]

S(0) = p геометр прогресс

S(0)p

C = 1 + (1+p)^-n


S(0)p(1+p)ⁿ – C(1+p)ⁿ + C = 0


Бетта - коэффициенты портфеля ценных бумаг


_n

Ожидаемая прибыль K = ∑ K_i P_i

ⁱ⁼¹


_{n n}

δ_i = K_i - K, δ^{2 =} ∑(K_i - K)P_i, δ = √∑(K_i - K)P_i – стандартное отклонение

^{i=1 i=1}

K_j =α + β K_M + ε_j, где K_j – ожидаемая прибыль по j-той акции,

K_M – рыночная цена портфеля,

ε_j – погрешность статистических расчётов.

_n

β_p = ∑ X_jβ_j, где β – коэффициент портфеля,

^j=1 X_j – процентная доля портфеля, вложенная в j-тую акцию,

β_j – бета-коэффициент j-той акции.


23Модель оптимизации Марковица

K= R(S)

p(S): ∑ p(S) = 1

_{n n}

Е[R] = ∑ K_i P_i, D[R] = ∑(K_i – m_R)² P_i,

^{i=1 i=1}

V_{ij =} ∑[R_i(S) - m_Ri][R_j(S) - m_Rj] p(S).


Марковицем. Согласно ей, требуется найти набор значений {X_i ≥ 0, i =1…I} таких, чтобы выполнялись условия

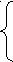
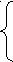_{I I n n}

∑ X_i = 0, либо ∑ X_i m_i ≥ m_п, либо ∑ ∑ V_ijX_iX_j ≤ V_п,

^{i=1 i=1 i=1 j=1}

_{n n I}

∑ ∑ V_ijX_iX_j → min, ∑ X_i m_i → max,

^{i=1 j=1 i=1}