«Площади»
| Вид материала | Документы |
- ТемЫ рефератов по мерчендайзингу, 204.9kb.
- Разработка урока по теме «Понятие площади многоугольника», 32.86kb.
- Механика Жидкостей и Газов, 12.81kb.
- Блиц (матан и триг.) блиц (геометрия) Вопросы по планиметрии, 56.04kb.
- Лабораторная работа №1 Тема: «Разработка простейших программ линейных структур», 169.83kb.
- Городские тематические экскурсии, 85.03kb.
- Урок-сказка по теме "Площади и объемы". 5-й класс, 87.63kb.
- Урок геометрии в 8 классе по теме «Площади многоугольников», 52.25kb.
- Об изучении площади в начальной и средней школе, 56.34kb.
- Доклад заместителя министра лесного хозяйства, 82.14kb.
Конструкции из интеграловссылка скрыта Статья отнесена к разделу: ссылка скрыта  В методической литературе всё чаще задаются вопросом: “Нужно ли изучать в школе интегралы?” На что с уверенностью можно ответить: “Конечно же!” И дело здесь не в том, что интегральное исчисление возникает раньше дифференциального в истории науки (а этот факт должен быть обязательно учтён при построении школьного материала), а скорее в том, что интегралы могут выступать не как самоцель, а как аппарат для закрепления базового материала. Часто при изучении интегрального исчисления в школе рассматриваются лишь основные моменты данного раздела: нахождение первообразных функции, вычисление определённых интегралов, отыскание площадей плоских фигур и объёмов тел вращения. Да, мы не спорим, что данные вопросы являются базовыми и необходимыми, ведь именно они раскрывают основную суть процесса интегрирования, но где же творческий подход в обучении математике? Где он? Именно на эти и другие возникающие вопросы мы постараемся ответить в своей статье. Порой мы просто-напросто ограничиваем тему "Интеграл" учебников и делаем её недоступной для другого математического материала, входящего в рамки школьной программы. Многие из учителей забывают, что, используя несложные конструкции, содержащие определённые интегралы, можно составить прекрасные уравнения, неравенства, их системы, различные задачи с параметрами, решение которых вызовет лишь положительное одобрение со стороны школьников. И это действительно так. Решая достаточно большое количество стандартизованных задач, учащиеся вскоре приходят к усталости, усталости решать "одно и тоже". В этот момент "мозговой штурм" сменяется "мозговым спадом", что на наш взгляд, не хотел бы наблюдать на своём уроке каждый учитель. И вот тогда на помощь могут прийти всё те же конструкции. Благодаря им, учащиеся будут стремиться вычислить не только сам интеграл, но и применить полученные в ходе вычисления результаты к решению конкретной задачи, которая в свою очередь вызовет интерес у школьников. Таким образом, нам удастся восстановить атмосферу сотрудничества на уроке и локализовать "штурм" в каждом из учеников. Составляя конструкции, мы сможем осуществить внутриматематическое моделирование, которое позволит доказать учащимся то, что тема "Интеграл" не существует сама по себе, автономно, а великолепно и в полном объёме используется при решении задач ранее изученных тем. Также одним из существенных моментов при решении задач, содержащих конструкции, является то, что учащиеся сталкиваются с тем, что в пределах интегрирования появляются переменные (до этого были лишь постоянные), для которых чаще всего приходится проводить анализ и находить их ОДЗ. Ведь вне ОДЗ многие определённые интегралы не вычислимы, тогда мы сталкиваемся с несобственными интегралами, решение которых не предусматривается школьной программой. Поэтому при составлении любых конструкций данный факт должен обязательно учитываться. Именно анализ заставляет учащихся сомневаться, делает процесс вычисления познавательным и привлекает к себе класс. Заинтересованный ученик всегда активен. Он стремится решить, понять, осознать. Поддержание данного стремления – основная задача учителя, его мастерство и профессионализм. В нашей статье мы приводим примеры некоторых из конструкций, которые могут быть использованы в конкретных ситуациях. К каждому заданию прилагается по два варианта с решениями. I. Решить уравнения. А) 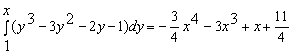 , ,Решение. Вычислим интеграл: 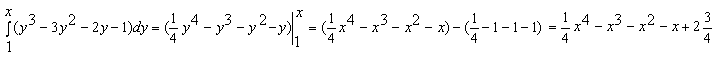 . .Тогда 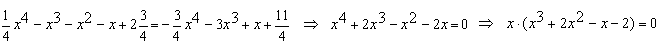 . Решая полученное уравнение, находим, что x = 0, x = + 1, x = – 2. . Решая полученное уравнение, находим, что x = 0, x = + 1, x = – 2.Ответ: – 2, – 1, 0, 1. Следует отметить, что в данном задании ничего не потребовалось, кроме техники нахождения простейших интегралов и решения уравнения, в том числе кубического. Б) 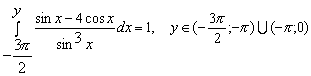 . .Решение. (В силу того, что интеграл неопределён при 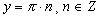 , то подобные точки выколоты из области задания). Вычислим значение интеграла: , то подобные точки выколоты из области задания). Вычислим значение интеграла: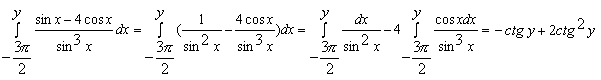 . . Для удобства проведём вычисления по отдельности: 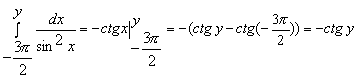 , ,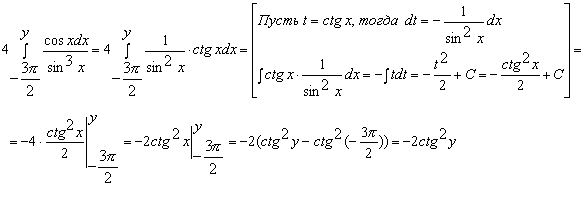 . .Приравнивая левую и правую часть равенства, получим: 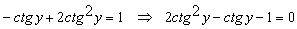 . Решая полученное тригонометрическое уравнение, имеем . Решая полученное тригонометрическое уравнение, имеем 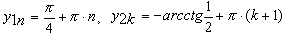 , где , где 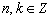 . . Но так как 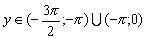 (по условию), то подбором устанавливаем, что (по условию), то подбором устанавливаем, что 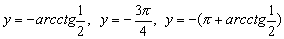 . .Ответ: 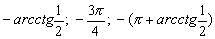 . .В данном задании учащимся приходится проводить исследовательскую работу с целью нахождения ОДЗ, решением тригонометрического уравнения, отбором корней. Здесь же они сталкиваются с вычислением нетабличного интеграла, для решения которого применяется подстановка, с которой многие учителя сталкиваются в своей преподавательской практике. Только правильный выбор подстановки и её использование приведёт к желаемому результату. II. Решить неравенства. А) 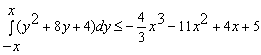 , ,Решение. Вычислим определённый интеграл: 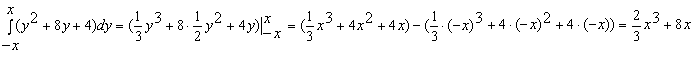 . . Тогда 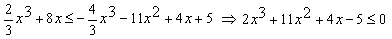 .Приравняем многочлен, стоящий в левой части к нулю и находим корни уравнения .Приравняем многочлен, стоящий в левой части к нулю и находим корни уравнения 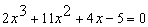 . Откуда . Откуда 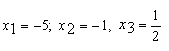 . Методом интервалов решаем неравенство . Методом интервалов решаем неравенство 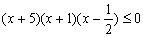 : откуда : откуда 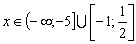 Ответ: 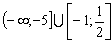 . .Б) 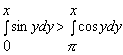 . .Решение. По отдельности вычислим интеграл, стоящий в левой части и интеграл, стоящий в правой части неравенства:  ; ;  . .Тогда 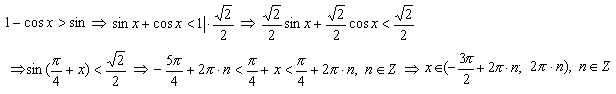 Ответ: 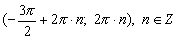 . .Существенных трудностей задания А) и Б) не вызывают. III. Оцените последовательности. А) 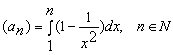 , ,Решение. Вычислим данный интеграл: 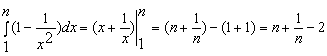 . .Пользуясь неравенством Коши для двух неотрицательных чисел, оценим выражение 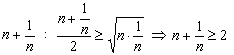 . .Прибавив к обеим частям данного неравенства – 2, получим оценку (an): 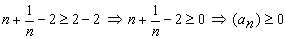 . .Ответ: 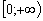 . .Б) 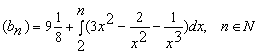 . .Решение. Вычислим определённый интеграл: 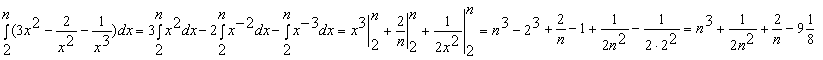 . .Тогда 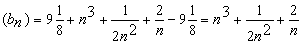 . .Используя неравенство Коши для трёх неотрицательных чисел, оценим (bn): 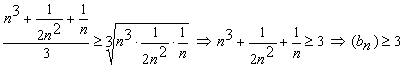 . .Ответ: 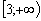 . .Вся трудность заданий А) и Б) заключается лишь в том, на сколько хорошо учащиеся помнят неравенство Коши. IV. На координатной плоскости изобразите множество точек (область), удовлетворяющих следующим условиям. А) 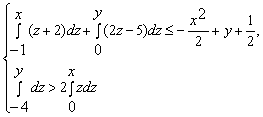 Решение. Преобразуем каждое неравенство системы по отдельности: 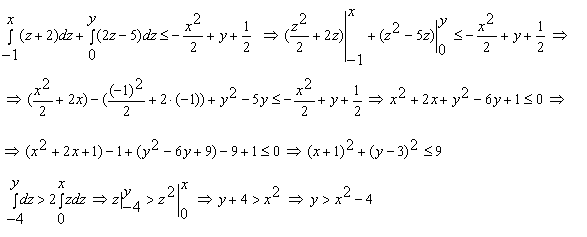 . .С учётом вычислений данная система примет вид: 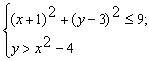 На координатной плоскости заштриховываем множества точек, удовлетворяющих каждому из неравенств системы: 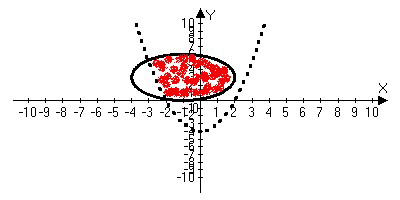 Закрашенная часть – искомая область. Закрашенная часть – искомая область.Б) 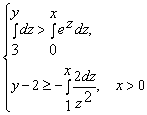 (данную конструкцию уместно предложить после изучения показательной функции). (данную конструкцию уместно предложить после изучения показательной функции).Решение. Преобразуем каждое из неравенств системы по отдельности: 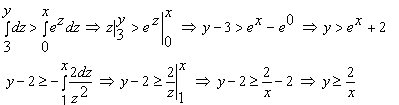 Тогда с учётом вычислений данная система примет вид: 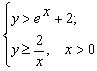 . На координатной плоскости заштриховываем множества точек, удовлетворяющих каждому из неравенств системы: . На координатной плоскости заштриховываем множества точек, удовлетворяющих каждому из неравенств системы: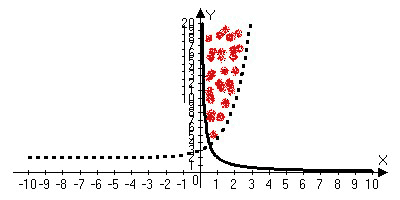 Закрашенная часть – искомая область. Закрашенная часть – искомая область.Сложность заданий А) и Б) заключается лишь в том, на сколько правильно учащиеся могут решать неравенства с двумя переменными. V. При всех значениях параметра решить уравнения. А) 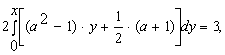 Решение. Для начала вычислим предложенный интеграл: 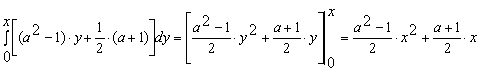 . .Тогда 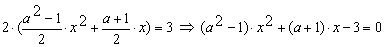 . Решая данное уравнение относительно параметра а, имеем: . Решая данное уравнение относительно параметра а, имеем:1. если a = – 1: – 3 = 0, сл., решений нет; если a = 1: получим линейное уравнение 2x – 3 = 0, сл., 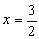 ; ;2. если 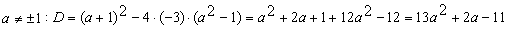 2.1. если 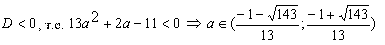 , то решений нет; , то решений нет; 2.2. если 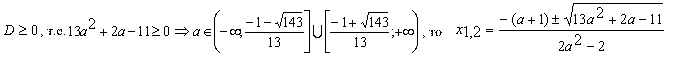 Произведя отбор, запишем ответ. Ответ: при 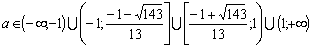 : : 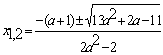 при 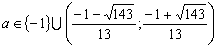 : решений нет : решений нетпри a = 1: 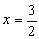 . .Б). 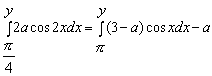 Решение. Вычислим предложенные определённые интегралы: 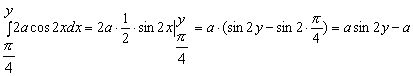 ; ;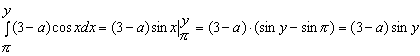 . .С учётом полученных вычислений имеем: 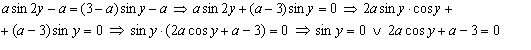 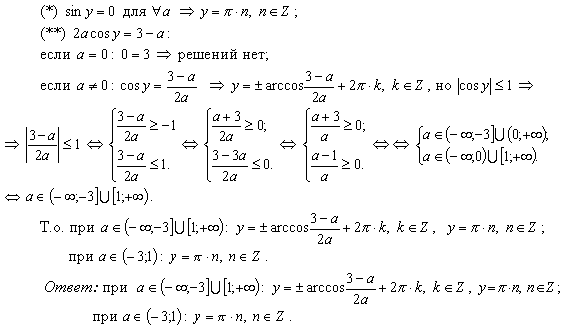 Во избежание ошибок при решении данного задания, необходимо заранее вспомнить с учащимися основные свойства тригонометрических функций (особенно области значений синуса и косинуса), а также правила решения отдельных задач с параметрами (это касается и задания А). В конце нашей статьи хотим ещё раз заметить, что добиться максимальной работоспособности учащихся на уроке можно лишь при постановке таких проблемных ситуаций, которые будут создавать у школьников стремление их разрешить. На наш взгляд, одной из таких ситуаций будет использование предложенных конструкций, которые и осуществят творческий подход при обучении математике. |
